基于参数灵敏度的漂浮物推拖船结构优化

郭 卫，倪 杰，吴培松

(苏州飞驰环保科技股份有限公司，江苏 苏州 215621)

0 引言

近年来，优化技术已被广泛应用于结构设计。船体结构的优化是寻求合理结构或材料参数，使船体结构在满足可靠性、稳定性、安全性要求下，具备更好的结构强度、生产工艺，并尽可能降低产品的成本。在对产品结构进行优化时，静态性能约束将使船体应力分布更为合理；同时，减小船体重量有利于优化船体动态性能并解决船体结构共振问题。因此在满足设计要求的前提下优化船体结构，实现船体结构的轻量化，并获得良好的动力学性能，具有重要的工程应用价值。

当前船体结构的优化主要集中于舱室结构、横截面、框架、舱板结构部件的结构优化，但由于涉及工作环境比较复杂，其除了承载船体结构重量外，还要承受风和波浪载荷的作用，因此对整个船舶的静态和动态性能设计给船舶结构设计提出了更高的要求。此外，整个船舶结构优化涉及到大量的计算变量和附加约束，存在较高的复杂度。

本文以自适应模拟退火算法为基础，以漂浮物推拖船为研究对象，基于参数灵敏度分析建立了漂浮物推拖船整体结构优化的数学模型，完成了结构的动静态优化设计。实验结果表明，通过灵敏度分析法可以减少整船结构质量和降低振动频率。

1 灵敏度分析

中型船舶板材厚度大，结构骨材尺寸较大。如果所有的板材厚度和整体参数直接作为设计变量进行优化，则优化效率较低且耗时，优化难度较大。因此，灵敏度的计算和分析是船舶结构整体设计中重要环节。通过对船体结构的目标函数及约束函数求解，可以反映变量对目标、约束函数等设计参数的影响。本文基于最大离差的理论，通过设置回归方程y=f(x1,x2,…,xn)，可以求出各参数设计变量xi的微小摄动，以及dxl的波动对y参数变化的影响，并基于dy值求出各参数的灵敏度Sxi。对各设计变量进行归一化处理，则可以计算得到各设计变量的标准灵敏度，基于归一化灵敏度，可以解除设计参数数量级上的差异。响应灵敏度的数值可以通过式(1)求得。

(1)

式中：Nxi为设计变量灵敏度Sxi与灵敏度数值总和的比值，即各设计变量的灵敏度所占百分比，且∑i∣Sxi∣=100，其值可取正值或负值。

本文采用归一化灵敏度参数化测试方法对每个结构设计变量的响应灵敏度进行分析，并以此为基础获得优化模型的设计变量。

2 优化模型

2.1 数学模型

结构设计优化模型的数学表达式见式(2)：

求:x={x1,x2,…,xn}T，使得：

minf(x)

s.t.gk(x)≤0 (k=1,2,…,m)

(2)

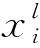
本文将质量最小化为优化的目标，并建立了相应的数学模型。

2.2 设计变量

漂浮物推拖船结构设计变量大致为两部分：一部分为船板结构设计变量，另一部分为船板结构所承受载荷变量。板的厚度变为整数，通过MSC Patran iSIGHT平台配置文件库功能模块分为离散集，从一组离散的值的集料规格变化的优化过程，通过所有的聚合参数优化改变集合变量，离散变量的约束条件有参数约束、载荷约束、振动约束。

(1)尺寸约束

(3)

(2)应力约束

(4)

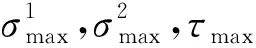
(3)结构变形参数约束

umax≤[u]

(5)

式中：umax为船体结构最大变形量集合；[u]为许用变形值。

(4)频率约束

fi∉(fimin,fimax) (i=1,2,…,n)

(6)

式中：fi为第i阶垂向方向的固有频率；fimin，fimax分别为频率变化的下限和上限。

2.3 船体结构优化方法

船体结构优化涉及多个变量，变量与响应的关系是一个高阶非线性关系。因此，设计空间的不连续性会出现优化滞后问题，这是很难实现的。粒子群优化算法是一种考虑全局参数变化的智能优化算法，尤其适用于多峰值、非平滑变化的非线性结构优化问题。由于粒子群优化算法不需要变量的性质，所以它的初始条件很低，且与初始值无关。其特点是优化参数通常绝对收敛，并且收敛速度较快，适用于求解离散设计变量。因此，采用自适应模拟退火算法对船体结构进行优化设计。

3 工程实例

以漂浮物推拖船整船模型作为研究对象，进行结构分析和优化。整个船体的结构主要包括板壳单元以及梁木单元模型，仿真结果表明：由MPC形成的云质量点质心位置、质量和船体的相应接触部分通过质量设定点云连接，模拟对应各舱内液体压力。

3.1 附连水质量参数对频率波动区间的影响

附连水质量可以通过路易斯图法计算求得。通过将船体进行不等间距离散，以路易斯经验公式计算粒子形式加载到在船体水线单位节点上。加载船体结构各节点附连水质量后，漂浮物推拖船结构的有限元模型如图1所示。

图1 全船有限元模型

船体结构振动源为发动机和螺旋桨。通过对整船结构的垂直方向的一阶和二阶固有频率进行分析，并将其所对应的固有频率作为约束，可以确定发动机的旋转频率区间，进而求出振动频率上下限。根据结构设计要求，基于频率的约束条件为：

f1≤2.917 Hz,f2≤3.125 Hz

(7)

式中：f1为一阶垂直方向的固有振动频率；f2为二阶垂直方向的固有振动频率。

3.2 全船结构模态分析

采用AtosLgoet法可以求得船舶结构的竖向振动的固有频率。图2和图3分别为对漂浮物推拖船整体结构的一阶和二阶垂向固有振动频率求解结果，其值见表1。

表1 全船垂向振动固有频率

从表1可以了解到，船体结构的二阶垂向振动固有频率不满足式(7)频率限制区域要求，可能会发生共振现象。 因此，有必要优化整船结构。

整船设计变量较多，共计157个。在动态特性优化过程中，分析了船舶结构的两阶自振频率和质量，并用灵敏度比约束设计变量。根据参数试验方法得到的两阶垂直自振频率的灵敏度和质量灵敏度计算结果，得到了二阶频率灵敏度和质量灵敏度比，其计算结果如图4所示。通过灵敏度的比值可以看出，船体结构优化能较好地识别并剔除消除灵敏度较大的设计变量，而保留下来的80个设计变量则为较为稳定的设计变量。

图2 一阶垂向固有振型

图3 二阶垂向固有振型

图4 二阶振动频率灵敏度与结构质量灵敏度比值 3.3 优化设计

优化模型的数学表达式为：

目标函数式(8)的优化目标是实现全船结构质量W最小化。其中：σVonmises为船体结构应力矩阵；τ为船体结构剪应力矩阵；σ梁为船体结构中梁单元的合成应力矩阵；f1，f2分别为船体结构的一阶和二阶垂直方向的振动固有频率；xi为结构设计变量集合，而各设计变量的上标l和u分别为变量的下限和上限。

3.4 船体结构优化与分析

通过粒子群优化算法对船体结构模型进行模拟，计算结果可知其模型在14.8 h后开始收敛，目标函数的迭代过程如图5所示。优化结果前后的一阶和二阶垂直固有频率与强度计算比较见表2。

图5 目标函数的迭代过程

参数质量/t一阶频率/Hz二阶频率/HzVon-mises应力/(N·mm-2)剪应力/(N·mm-2)梁合成应力/(N·mm-2)变形/mm优化前157.571.658 93.572 9124.885.777.126.9优化后127.571.572 23.000 1136.690.699.729.8

从有限元分析结果可知：

(1)本文对漂浮物推拖船结构优化，各参数变量为可行域的有效解，其优化结果能够满足所有结构参数的应力、变形和频率约束条件。

(2)除个别设计变量，如艉盖厚度、艉板加强筋规格、泵板龙骨厚度等，大部分设计变量值都有所减小，其中板材厚度减小幅度要大于其他设计变量的减小幅度，这说明结构固有频率和结构厚度的影响大于骨材质量指标，且与灵敏度变量分析的结果是一致的。

(3)优化后，全船总质量为24.69 t，比初期的30 t降低了5.31 t。这一结果表明，通过结构优化可以在保证整船性能的前提下，节省船体结构钢料，降低项目成本。

(4)优化后，一阶垂直频率减少0.086 7 Hz，二阶垂直频率下降0.572 8 Hz，提升了结构的频率裕度，降低了共振出现的可能性。特别是优化后的二阶垂直固有频率小于3.264 Hz，实现了优化的初始目标。

上述优化模型是在满足频率约束的条件下实现船舶质量最小化，并通过优化板厚和聚集模型等离散变量，获得了质量约束条件下的船舶结构频率优化模型，使得整船结构参数满足船体结构参数设计要求，并且保证船体结构变形和应力均满足约束条件。以自然频率最小化为优化目标，采用自适应退火算法求解二次优化模型，实现整船结构的二阶垂直振动固有频率f2收敛。

4 结论

本文将灵敏度分析方法用于分析整船结构特征参数优化。基于灵敏度分析方法建立的船体结构的静态和动态优化模型是以实现全船结构质量W最小化作为目标，优化后整船结构在满足船体结构强度和刚度的条件下，实现了较为理想的轻量化和良好的减振效果。这表明，对于优化问题，优化目标和约束函数可以通过配置设计变量上限和下限发挥较好的约束作用，以实现整船结构和性能的优化。

参考文献:

[1] Zhu T Y, Toshiyuki S. Design loads used for direct strength assessment of merchant ship structures[J].The American Society of Mechanical Engineers, 2007,129(2)： 120-130.

[2] 刘俊,汪庠宝,韩继文.运用NASTRAN进行波浪载荷作用下船体强度分析[J].上海交通大学学报, 2005, 39(5)：711-714.

[3] 张少雄,陈南华,张伟. 8 000吨级江海直达驳船的全船结构强度直接计算[J].船海工程, 2005(5)：39-41.

[4] 顾永宁,腾晓青,戴立广.大开口型船舶波浪诱导载荷研究[J].船舶工程, 1998(4)：5-8.

[5] 白建伟,李润培,顾永宁.集装箱船整船有限元结构分析[J].船舶工程, 2000(5)：8-11.

[6] 朱仁传,缪国平,林兆伟,等.运动船体甲板上浪的数值模拟[J].水动力学研究与进展(A辑),2008, 23(1)：7-14.

[7] 周勤俊,王本龙,兰雅梅,等.海浪越浪的数值模拟[J].力学季刊,2005,26(4)：629-633.