基于Sepic逆变器抑制无刷直流电机换相转矩脉动研究
2018-06-05
(福州大学电气工程自动化学院,福建 福州 350108)
1 引言
直流无刷电机(BLDCM)在某种意义上来说是隶属于同步电机,简而言之转子的转速与定子旋转磁场的速度和转子极数有关。直流无刷电机在拥有传统直流电机的优点上同时又取消了碳刷、滑环结构,使其增加许多特性:无级调速、调速范围广、过载能力强、可靠性高、稳定性好、适应性强、维修与保养简单等。转矩特性是电机性能的重要指标,无刷直流电机的换相、齿槽效应、电枢反应等,都会产生转矩脉动。齿槽效应、电枢反应产生的转矩脉动可以通过电机设计来减少。因此,无刷直流电机的转矩脉动主要来源于换相时产生的转矩脉动。有效的控制减少无刷直流电机换相时刻产生的脉动,就能使电机稳定运行。
2 永磁无刷直流电机的数学模型
定义电机采用星型绕线方式,转子结果为面贴式的永磁无刷直流电机。在此电机结构基础上,为了简化数学模型,作出以下几点假设:
(1)不考虑换相时电流变化的过度过程;
(2)电机定子铁心气隙磁导均匀,不计涡;
(3)流损耗和磁滞损耗;
(4)忽略定子齿槽效应和定子绕组的电枢反应;
(5)逆变电路的开关管和续流二极管均为理想开关器件;
(6)三相定子绕组完全对称,两相绕组空间相差120°。
根据以上假设,电机的电压平衡方程式为:
(1)
式中:ua,ub,uc—每相绕组相电压(V);
ia,ib,ic—每相绕组相电流(A);
ea,eb,ec—每相绕组相反电势(V);
Ra,Rb,Rc—每相绕组相电阻(Ω);
La,Lb,Lc—每相绕组相自感(H);
Mab,Mac,Mba,Mbc,Mca,Mcb——每两相绕组间互感(H)。
因三相定子绕组完全对称,则相绕组之间的电阻均相等:
Ra=Rb=Rc=R
(2)
电机采用面贴式转子结构,从磁路分析上看,绕组的自感和相间互感不会随着转子的位置变化而变化。所以三相定子绕组的自感和绕组间的互感为固定值,即:
La=Lb=Lc=Ls
(3)
Mab=Mba=Mac=Mca=Mbc=Mcb=M
(4)
由于采用星型连接,则有:
ia+ib+ic=0
(5)
联立式(2)、(3)、(4),可以将式(1)化简为:
(6)
式(6)对应的等效电路图如图1所示。

图1 电压方程等效电路图
以A相为例,电机A相反电动势可以表示为:
(7)
式中:ω—电角速度(rad/s);
Ψm—永磁磁链幅值(Wb);

Ω——机械角速度(rad/s);
p——极对数。
电机输出的电磁功率等于每相绕组的反电动势和电流的乘积之和:
Pe=eaia+ebib+ecic
(8)
式中:Pe——电磁功率(W)。
忽略电机的机械损耗,电磁转矩可以表示为:
(9)
式中:Te——电磁转矩(N*m)。
根据式(7)和式(9)可得电磁转矩方程的另外一种形式:
(10)
当永磁无刷直流电机运行在120°导通工作方式下,不考虑换相暂态过程,三相Y接定子绕组中仅有两相流过电流,其大小相等且方向相反。注意到f(θ)平顶处的符号对不同相绕组而言总是相反的,因此式(10)可以进一步化简为:
Te=2pΨmia=KTi
(11)
式中:KT—电机转矩系数;
I—稳态时的绕组相电流。
包括上述电压方程和转矩方程在内,要构成一个机电系统的完整数学模型,还需要引入电机运动方程:
(12)
式中:TL—负载转矩;
J—转子转动惯量;
Bv—黏滞摩擦系数。
式(6)、(9)和(12)共同构成了永磁无刷直流电机的微分方程的数学模型。
2.2 永磁无刷直流电机换相转矩脉动原理及抑制策略
在电机换相暂态过程中,电流和反电势均发生变化,两者之间互相影响,导致换相转矩波动。
以全桥驱动的三相对称绕组Y接无刷直流电机为例。电机电压方程为
Ux=Rix+(L-M)dix/dt+ex,x=A,B,C
(13)
式中:Ux就相电压;ix相电流;ex相反电动势;R相电阻;L相绕组自感;M相绕组互感。
电磁转矩方程为:
Te=(eaia+ebib+ecic)/Ω
(14)
式中:Ω电机的机械角速度。
要保持电磁转矩恒定,在转速一定时,eaia、ebib、ecic之和必须恒定。假定电机本身气隙磁场分布为理想梯形波,反电动势与磁通密度分布一致。因此,要保持电磁转矩恒定,必须使电枢电流为方波且与ex同相位。对于三相桥式驱动无刷直流电机来说,稳定时只有两相电枢绕组导通,另一相悬空,如图2所示。
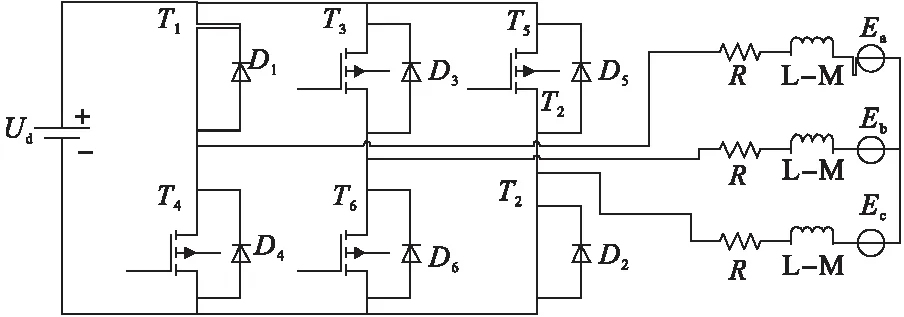
图2 永磁无刷直流电机换相前
假设换相前A、C相导通,ic=-ia,ib=0,ec=-ea,因此,Te=2ecIc/Ω。
设此时ic=-I,ec=-E,则T=2EI/Ω,此时电磁转矩为平均转矩。当控制器发出换相信号后,T1关闭T3导通,此时状态如图3所示。

图3 永磁无刷直流电机换相中
忽略相电阻且认为相反电动势保持理想波形,此时相电流变化为:
(15)
由于换相过程持续时间很短,在此过程中认为ea=E。可以得到换相瞬间相电流与时间的关系:
(16)
由于此时ia仍然存在,电流只有通过续流二极管续流,直到ia减少为零,如图(4)所示。

图4 永磁无刷直流电机换相后
在此过程中,ib由零增加到I,而且仍然满足;
ia+ib+ic=0
换相结束后ia=0,ic=-ib。定义ia由I减少到零的时间为t1,ib由零增加至I的时间为t2。各相电流变化过程可近似如图5所示。

图5 不同条件下换相期间各相电流波形
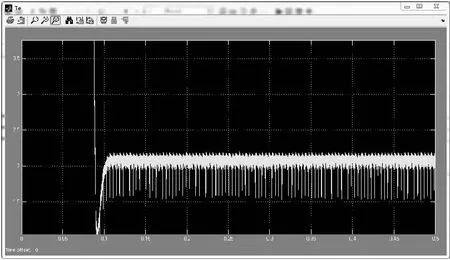
由式(13)可知,换相前转矩T可以看成只与ecic有关系(成正比)。在换相过程中,当t1>t2时,ic幅值大于I;在t1=t2时,ic幅值一直保持恒定;在t1 (17) 经过tfa时间后,ib的值为: (18) 由式可知以下结论: (1)当Ud>4E时,t1>t2,换相期间转矩增大; (2)当Ud=4E时,t1=t2,换相期间转矩不变; (3)当Ud<4E时,t1 由此可见,在Ud=4E时,可以避免Ic的幅值的波动,不会产生换相时的转矩脉动。但是,Ud=4E不是电机的稳定状态,是加速状态。当转速增加时反电动势E也会增大,此时就产生了转矩脉动。因此在稳定状态下,无刷直流电机换相转矩脉动与转速有关。 所研究的永磁无刷直流电机的新型控制方法是在三相逆变器前段加一个附加电路和开关选择电路,电路图如图6所示。 图6 当VS1处于通态时,US-L1-VS1回路和C1-VS1-L2回路同时导电,L1和L2贮能。等效电路图如图7所示。 图7 此时,Ul1=Us,Ul2=Vc1。 VS1处于断态时,US-L1-C1-VD1-负载回路及L2-VD-负载回路同时导电,此阶段US和L1既向负载供电,同时也向C1充电,C1贮存的能量在VS1处于通态时向L2转移。等效电路图如图8所示。 图8 此时,Us-Ul1-Uc1-U0=0.Ul2=-U0,根据电感伏秒积平衡可得: DUs+(1-D)(US-U0-Uc1)=0,DUs+(1-D)(-U0)=0 解得Uo=DUs/(1-D)Us。 根据控制附加电路VS1的占空比D的大小得输出电压:U0=DUs/(1-D)。由于反电动势与转速成正比,即Em=Kew。由U0=DU/(1-D)和Em=Kew可以得到换相期间的D=4Kew/(Us+4Kew)。由此可知,通过实时测量转速,可得附加电路开关管的占空比,从而得到期望的换相直流电压,满足Udc=4Em实现转矩的恒定。 由于换相时间相对较短,而附加电路输出时间较长,为确保电压响应速度,在电路结构中加入开关选择电路,实现对直流侧电压的控制,在非换相导通期间,VS2开通,VS3关断,逆变器由Us供电,当换相信号到来的时候,VS3开通,VS2关断,逆变桥由附加电路供电。 根据式(5)电压方程建立起永磁无刷电机的定子侧模型,输入为电压和反电势,输出为电流。如图9所示。 图9 定子侧模型 转子磁链和反电势由查表得到,由转矩平衡方程得到转速位置角,最终得到永磁无刷直流电机模型,如图10所示。 图10 无刷直流电机数学模型 图11 永磁无刷直流电机控制系统结构图 建立了永磁无刷直流电机控制系统,使用电压源型逆变器供电,在非换相时刻g1信号触发VS2导通,电压源直接接入至逆变器。当换相信号来时,g2信号触发VS3导通,电压源通过附加升压电路再接入逆变器。g3信号通过永磁无刷直流电机反馈回来的数据来输出PWM波。 利用MATLAB的SIMULINK对永磁无刷直流电机采用附加电路和不采用附加电路进行了仿真。仿真实验的电机参数为:额定电压 220V,额定转2500rpm,C1=5× 10-4F,L1=L2=5× 10-4H,相电阻R=1Ω,相电感L=20mH,电机的转动惯量J=5×10-3kg·m2,反电势系数Kv= 0.4536V/rpm,给定2N的负载转矩。不采用附加电路的母线电流波形如图12所示。 采用附加电路的母线电流如图13所示。 对比发现,采用了附加电路的永磁无刷直流电机的母线电流在平顶处更趋近于平稳,相比于不采用附加电路的永磁无刷直流电机的脉动更小。由于Te=KTi,相对的换相转矩脉动也得到了抑制。不采用附加电路的转矩脉动波形如图14所示,采用附加电路的转矩脉动波形如图15所示。 图12 图13 图14 图15 分析两种情况下的转矩脉动,采用附加电路控制情况的转矩在1.9~2.1之间波动,而没采用附加电路控制的转矩在1.6~2.2之间波动。显然采用附加电路控制大大的抑制了转矩脉动。 实验中采用以TMS320F2812 DSP为核心的全数字控制平台。本系统的实验平台包含电源、控制板DSP开发板、电机、磁粉制动机、磁粉张力控制仪、示波器。磁粉制动器为电机提供负载,磁粉张力控制仪控制磁粉控制器的制动输出扭矩如图16所示。 图16 为了验证抑制转矩脉动的效果,分别在采用附加电路和未采用附加电路的情况下做了两组实验:(1)给定转速1800r/min,空载;(2)给定转速1800r/min,负载转矩0.6N·M。 无刷直流电机参数:额定电压 24V、额定功率 105W、额定转速 3000rpm,力矩常数0.063NM/A、反电动势常数:6.6V/krpm 。 磁粉控制器参数:转矩 1N、电压 24V、功率10W。 两种控制策略的电流,转矩实验波形分别如图17,图18和图19。 图17 母线电流波形 根据母线电流波形和转矩波形来看,采用附加电路的电流波形,平顶部分更趋近与直线,相对的他空载转矩波形和负载转矩波形脉动更小。由图可知,空载情况和负载情况下的转矩最大脉动分别为0.05N·m和0.07N·m;未采用附加电路空载情况和负载情况下的转矩最大脉动分别为0.1N·m和0.14N·m。因此,在换相期间加入个升压附加电路能够改善母线电流波形同时还能够抑制转矩脉动。 图18 转速为1800r/min,空载情况下的转矩波形 图19 转速为1800r/min,负载转矩为0.6N·M情况下的转矩波形
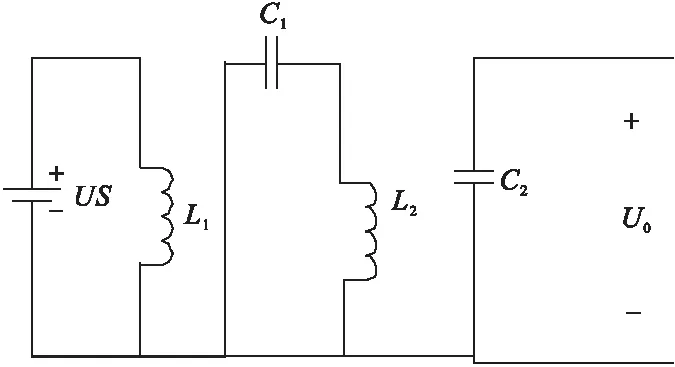

3.1 永磁无刷直流电机抑制转矩脉动策略模型的建立


3.2 控制系统模型的建立

4 实验现象和结果分析



4.2 实验结果分析