基于Delta调节器的微网逆变器控制策略研究
2018-06-05黄潇潇杨海兴
朱 辉, 黄潇潇, 杨海兴
(1. 国网天津市电力公司 城西供电分公司,天津 300113; 2. 国网天津市电力公司 电力科学研究院,天津 300384; 3. 河北省送变电有限公司,河北 石家庄 050000)
0 引言
随着功率半导体器件开关速度和额定容量的提高,在光伏发电、电动汽车充电和和分布式储能装置等领域,电压源型逆变器受到了越来越多的关注[1~3]。传统的控制负载输出电流或者输出功率的方法是利用晶闸管可控整流器和开关频率恒定的逆变器实现这一过程的。但是整流器中的开关器件通常工作在硬开关状态,进一步增加了功率损耗以及设备的体积和重量[4]。
电压源型串联谐振逆变器工作在零电流开关状态,逆变器控制方法包括闭环控制、无差拍控制和重复控制等。单闭环电压控制方法虽然控制结构简单易于实现,但是动态响应性能差[5]。电压和电流双闭环控制尽管动态响应特性快,但是控制参数设定取值复杂[6]。而无差拍控制与重复控制虽然控制误差值低,但依赖于复杂数学模型的建立[7,8]。综上所述,提出了一种应用于串联谐振逆变器的电流可调Delta调节器CRDM(Current Regulated Delta Modulator),控制脉冲序列的产生,这种方法采用高增益的bang-bang调节器,因而具有较强的鲁棒性和响应速率[9]。但是CRDM控制输出电流常伴随有非零稳态误差和偏置,导致输出功率性能恶化。本文通过对工作在零电流开关状态下的串联谐振逆变器进行动态电流模型分析[10],提出一种改进的带有积分复位功能的CRDM调节器,通过引入积分复位环节,减小直流侧电流偏置,提高电网侧功率因数,通过仿真分析和实验验证了提出的控制策略。
1 零电流开关串联谐振逆变器动态电流模型
为了对电流可调Delta调节器进行简化并进行有效地分析,首先提出了一个基于串联谐振逆变器的离散时间动态模型,其原理如图1所示,其中负载电路由等效电抗Leq、电阻Req和电容Cc串联连接。

图1 串联谐振电路原理图
已知匹配变压器二次侧输出电压初始值为Vs,对应时刻t=0,输出电流io。槽路电容电压vc的简化表达式可以表示为公式(1)和(2):
(1)
(2)
式中:α为衰减系数;Q为品质因数;ωr为固定角频率;ωd为时域角频率;φ为相位。
式中:vc为等效负载电容电压;Vs为输出电压初始值;io为输出电流;Leq为等效电抗;Req为等效电阻;Cc为等效电容。
由于每一个功率开关器件总是在电流过零点时刻改变其开关状态,因而开关器件的开关频率总是等于负载谐振频率。串联谐振电路输入端电压值由逆变器开关状态决定,如公式(3)所示。
(3)
式中:Vdc为输入端电压值。
定义一个离散变量M(k)来描述逆变器的运行模式,如公式(4)所示,
(4)
结合公式(3)和(4)可以写成:
vs(t)=VdcM(k)sign(io(t)),
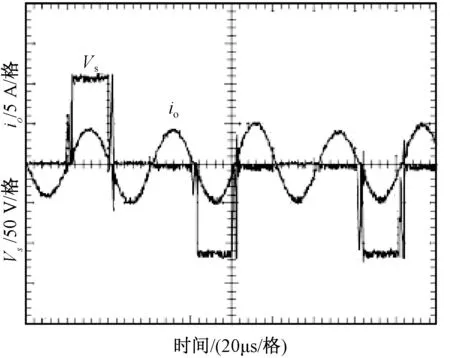
kT (5) 式中:T=π/ωd,代表半个谐振周期;sign(io(t))为输出电流符号函数。 由式(1)(2)和(5)可得: (6) Vc(k+1)=|vc(kT+T)|= (7) 式中:Io(k)为负载输出电流状态量;Vc(k)为电容电压状态量;负载品质因数Q≫1,ωd≈ωr,φ≈0。 将公式(7)代入(6),可以得出离散时间下的电流Io(k+1): Io(k+1)=ΦIo(k)+Γu*(k+1) (8) 式中:Io(k)为输出电流离散状态量;u*(k)为等效控制输入量;Φ和Γ为调节系数。 (9) (10) (11) 式(11)的等效控制输入u*(k+1)取值范围为{1,0.5,0,-0.5,-1},则流过负载线圈的输出电流最大值可以由式(8)(9)和(10)得出: (12) 式中:Imax为输出电流最大值。 在一个采样周期内,负载电流的变化决定了电流纹波的幅值,关系表达式为: (13) 式中:ΔI(k)为电流纹波幅值状态量。 对于阶跃输入指令,电流控制器的瞬时响应速率快,超调量小。由式(8)可知,零电流开关串联谐振逆变器工作在常规采样系统下,图2(a)显示了电流可调Delta调节器的控制原理图。由式(13)可知,在这种情况下,控制输入值只有0和1两个状态,输出状态切换速度或者电流变化速率不能被恰当地调整,导致直流侧电流纹波含量高,电流偏置大。因此,为了减小偏置值,在传统的CRDM调节器的前馈通道上加入了一个积分器,控制原理如图2(b)所示。 图2 电流可调Delta调节器(CRDM) 变结构控制理论常被用于分析具有开关性质的系统[11,12]。基于滑模变结构控制的开关状态可以表示为: S(k)=Ie(k)+Kiz(k) (14) 式中:S(k)为滑模变结构控制开关状态量;Ie(k)为误差电流状态量;Ki为积分器增益;z(k)为积分增益系数。 z(k+1)=z(k)+TIe(k) (15) 对应的M(k+1)的值为: (16) 为了满足滑模变结构控制要求,需要满足以下条件: S(k){S(k+1)-S(k)}<0 (17) 则平均误差的动态特性可以由S(k)=0这一时刻对应的误差值决定如下: Ie(k)=e-KiTIe(0) (18) 由式(18)可知,适当增大积分增益Ki可以更好地减小直流偏置。为了进一步扩大Ki的上限值,当直流侧电流误差值大于预设的误差带宽η时,积分器被强迫复位,控制原理如图3。每半个谐振周期内,采集逆变电路直流侧电流值Io,与参考电流值Iref进行比较,产生误差信号Ie。PI控制器的输出信号经过bang-bang调节器的调节决定下一时刻逆变器的运行模式[13]。借助这种控制方法,通过合理地设计积分器增益Ki和误差带宽η,可以有效地减少直流电流偏置,避免较大超调量的产生,同时也可以保证负载输出电流的连续性。 图3 加入积分复位的电流可调Delta调节器控制原理图 首先,确定积分增益Ki的最大值,考虑式(14)中的积分增益系数z(k),当z(k)=1时,直流侧电流误差的幅值Ie(k)等于S(k)。为了满足式(17)滑模控制的要求,可以联立式(8)(14)和(15),得出S(k): S(k+1)-S(k)=(1-Φ)Io(k)-Γu*(k+1)+ KiTIe(k)=-ΔI(k+1)+KiTIe(k) (19) 当S(k+1)-S(k)=0,解得Ki: (20) 式中:Iref为电流参考值。 当控制输入信号M(k+1)=1时,u*(k+1)可能的取值为{1,0.5}。当u*(k+1)=1时,Ki满足: 0 (21) 式中:K1为在u*(k+1)=1且Ie(k)>0时对应的Ki值。 当控制输入信号M(k+1)=0时,u*(k+1)可能的取值为{0,0.5}。当u*(k+1)=0时,Ki满足: 0 (22) 式中:Ko为在u*(k+1)=0且Ie(k)<0时式(20)对应的Ki值。 当u*(k+1)=0或1时,由式(21)(22)可得Ki满足: (23) 但是,当u*(k+1)=0.5时,Ki无法解出,此时对应S(k)<0,Io(k)<0.5或者S(k)>0,Io(k)>0.5两种情况,为了减少这种情况下的电流纹波,下一时刻S(k+2)的值应满足: S(k){S(k+2)-S(k+1)}<0 (24) 此时,u*(k+2)的可能取值为{1,0},并同时满足M(k+2)=M(k+1)。借助上述式(23),当满足Iref=Imax或者Iref=0时,可以得出: (25) 然后确定误差带宽η的最小值。为了减小超调量,需要选取一个较小的η值,同时满足在稳态情况下最大电流误差值不使积分器复位。图4(a)显示了当Iref<0.5Imax情况下误差带宽η值,图4(b)显示了当Iref>0.5Imax情况下误差带宽η值,再结合式(23)(24)和(25),得出误差带宽η最小值为: ηmin=max{|ΔI(u*=0.5)|+|ΔI(u*=1)|, (26) 图4 不同Iref下对应的电流误差和控制输入值 为了验证提出的电流可调Delta调节器的控制性能,使用一个额定功率5 kW、工作频率100 kHz的逆变器系统,主要参数为:Vdc=120 V,Req=0.5 Ω,Leq=20.0 μH,Cc=0.12 μF,N=3,Q=26,Imax=72 A。 图5显示了当参考电流值为60 A时的电流误差Ie稳态响应波形。其中图5(a)对应的是在传统CRDM控制下的稳态电流误差波形,误差值基本维持在2 A左右,对应误差率为3.3%。图5(b)中加入了复位积分器,稳态偏置进一步减小,由式(25)中计算可得积分增益最大值为 12 000。当Ki值过大会导致直流侧电流纹波含量增加,波形对应图5(c),其中Ki=100 000。 图5 直流侧电流稳态误差仿真波形 图6中的(a)(b)两条曲线分别表达了不同误差带宽值对应的阶跃输入信号下的输出电流Io响应波形,其中积分增益Ki=10 000。由图6可知,当误差η=6.5 A,满足最小误差带宽时,直流侧电流响应超调量几乎为零;而当η=20 A时,超调量较大。 图6 当参考电流值Iref=60 A阶跃响应波形 图7显示了当0.4 ms时,负载由Req=0.5 Ω到0.25 Ω变化和当0.8 ms时,负载由Req=0.25 Ω到0.5 Ω变化控制器的输出响应波形。在此过程中,本文提出的电流控制器表现出了较强的电流调节性能,误差值维持在允许的范围内。 图7 当t=0.4 ms和0.8 ms时负载变化时电流波形 为了验证上述理论分析与仿真过程,设计了一台单相逆变器实验样机,其主要参数为:额定功率25 kW,额定输出电压200 V,开关频率为22 kHz;主电路开关器件选用IGBT双管结构;积分增益Ki= 10 000,误差带宽η=8.2 A。 图8为加入积分复位器前的Delta调制谐振逆变器负载输出电压和电流波形。加入积分复位器前,谐振逆变器在换流过程中开关损耗大,负载输出电压和电流尖峰明显。 图8 未加入积分复位器时的负载输出波形 图9为加入积分复位器后Delta调制谐振逆变器负载输出电压和电流波形。开关损耗明显减小,负载电压和电流波形尖峰消失。 图9 加入积分复位器之后的负载输出波形 本文研究了一种基于零电流开关串联谐振逆变器的微网逆变器结构及控制策略,通过在传统的电流可调Delta调节器中加入具有复位功能的积分器,进一步减小了输出电流的稳态偏置值,同时保持纹波电流含量在一个较低的水平,瞬时响应超调量几乎可以忽略。通过仿真分析和研制25 kW单相实验样机验证了电流控制器的调节性能。 参考文献: [1]李啸骢,任子熠,袁辉,等.基于多指标非线性控制方法的微网逆变器控制设计[J].电力自动化设备,2017,37(9):18-23. [2]余畅舟,张兴,刘芳,等.组串式LC型光伏逆变器并网谐波环流及其抑制策略分析[J].电力系统自动化,2016,40(13):77-84. [3]刘东奇,钟庆昌,王耀南,等.基于同步逆变器的电动汽车V2G智能充放电控制技术[J].中国电机工程学报,2017,37(2):544-557. [4]姚广平,张永盈,林康红.一种适应电源频变的晶闸管三相全控整流桥α角控制器[J].电测与仪表,2015,52(21):102-105. [5]陈堃,周友斌,徐华安,等.基于电压控制的逆变器无互联线并联控制研究[J].电力电子技术,2017,51(1):82-85. [6]李燕青,王子睿.dq0坐标系下微网电压电流双闭环下垂控制方法及其逆变器设计[J].华北电力大学学报(自然科学版),2017,44(1):39-45. [7]王坚,王毅,胡灿,等.MMC型光伏并网逆变器无差拍控制策略[J].电力科学与工程,2017,33(9):8-14. [8]张学广,马彦,李瑞,等.两相静止坐标系下并网逆变器的重复控制策略[J].电工技术学报,2016,31(9):85-91. [9]甄文超. 基于Delta逆变器式三相串联补偿交流稳压源的研究[D].内蒙古:内蒙古科技大学,2014. [10]李春来,刘卫亮,王印松,等.基于FPGA的微网储能逆变器电压逆控制方案实现[J].电力科学与工程,2016,32(2):43-49. [11]樊英,周晓飞,张向阳,等.基于新型趋近律和混合速度控制器的IPMSM调速系统滑模变结构控制[J].电工技术学报,2017,32(5):9-18. [12]严广,蔡世冠,张旭,等.电网不平衡下PWM整流器滑模变结构控制[J].电力电子技术,2017,51(1):1-3. [13]陆翔,谢运祥,桂存兵,等.基于多滑模变结构控制的三相PWM整流器非线性控制[J].电工技术学报,2016,31(4):79-87.2 采用积分复位的电流可调Delta调节器


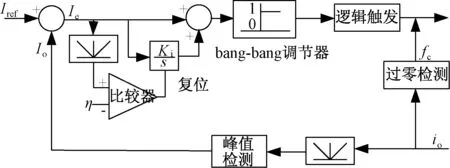
3 带有复位功能的积分器设计

4 仿真过程分析

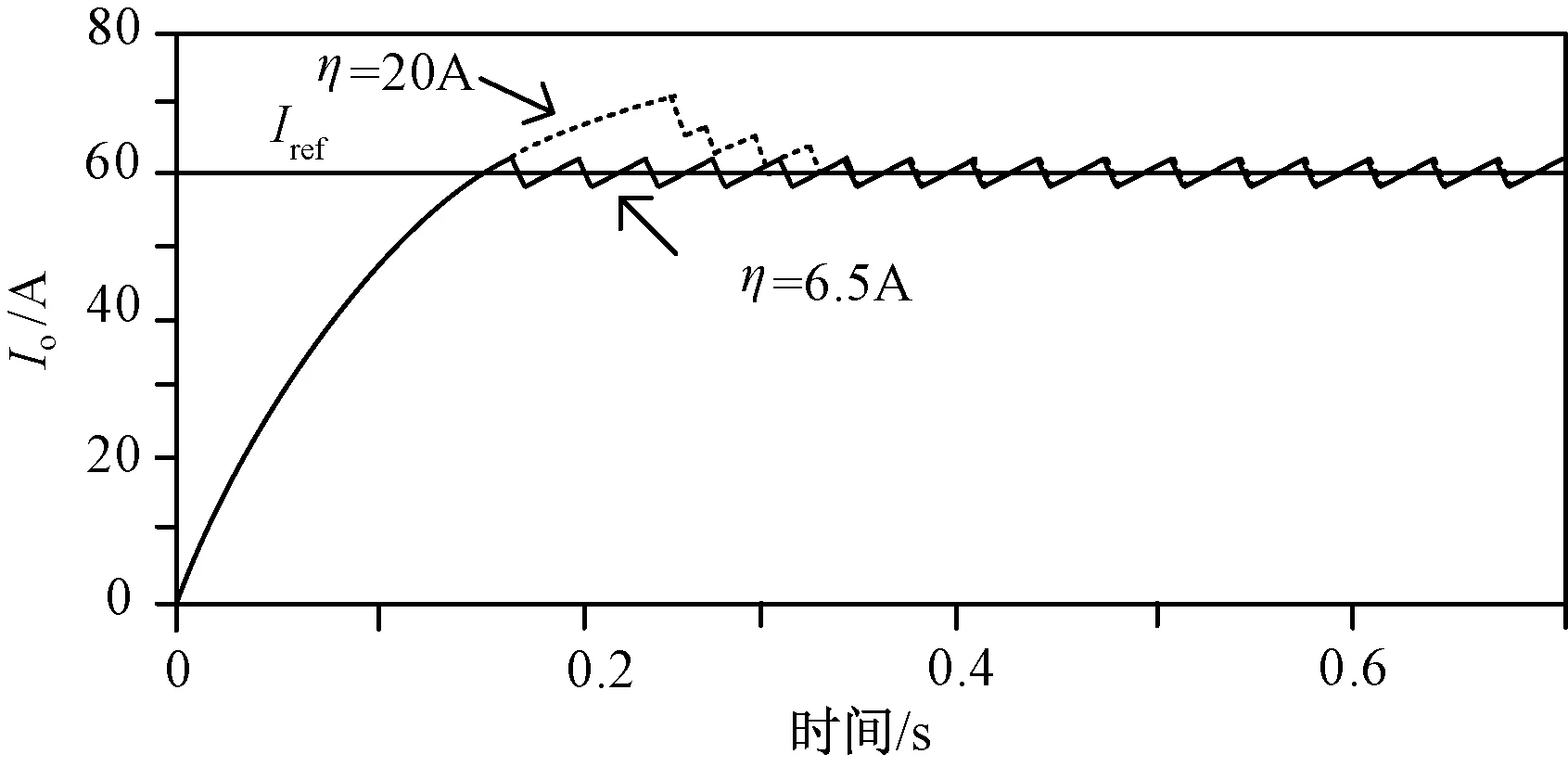
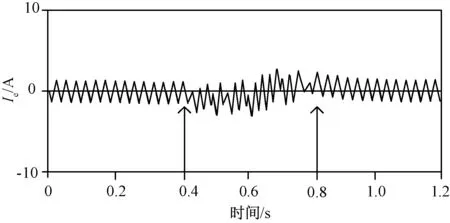
5 实验结果
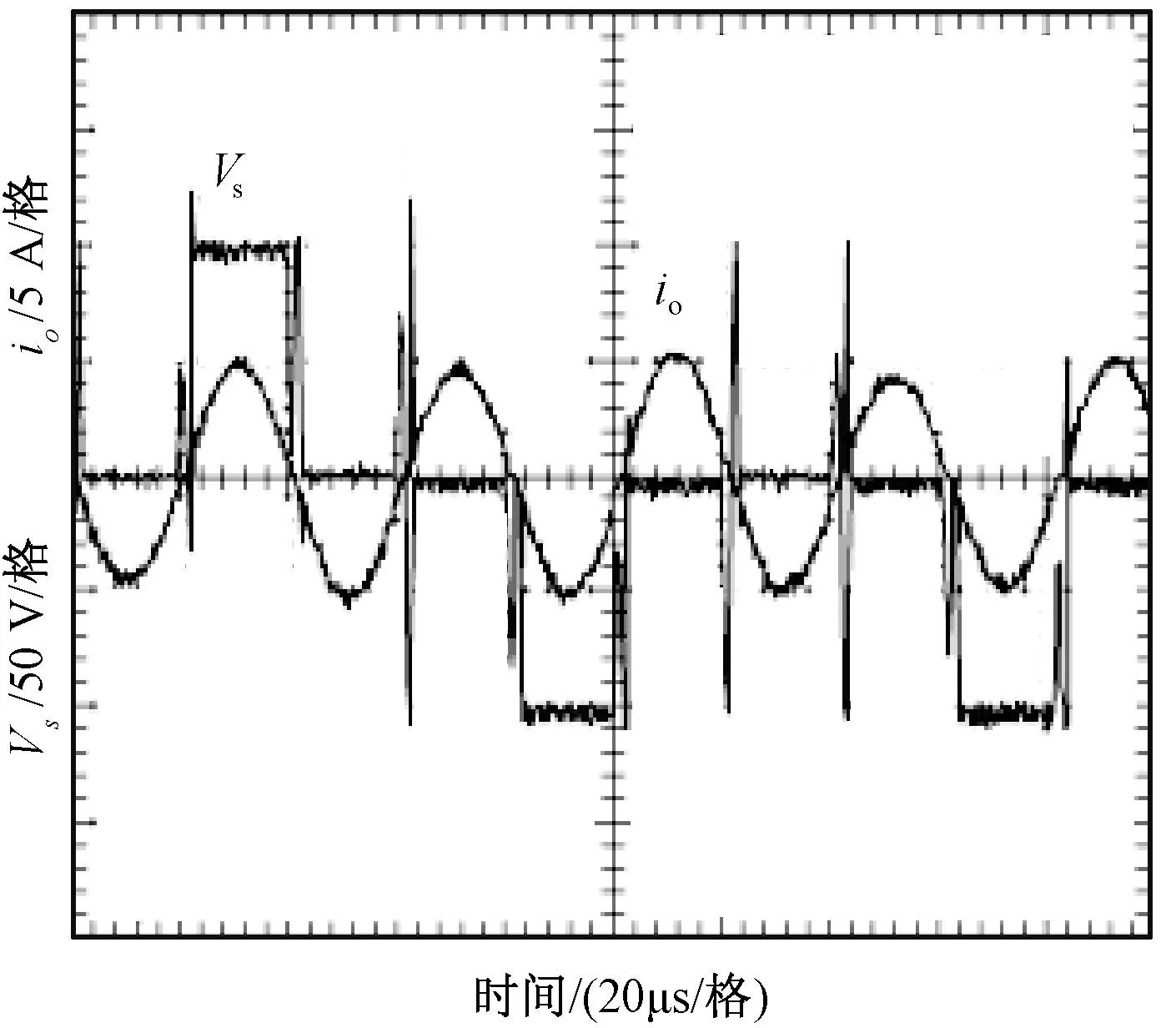
6 结论
