多变量过程闭环辨识在稳压器中的应用

胡云波， 张 伟

(上海理工大学 光电信息与计算机工程学院，上海 200093)

0 引言

稳压器是核电场反应堆里十分重要的装置之一，其稳定运行对整个核电站有着特别重大的意义。在对核电站的仿真控制中，准确建立稳压器的数学模型是获得理想控制效果的必要条件。实际情况中，稳压器并不是单一的输入输出系统，其压力与液位之间存在着复杂的耦合关系[1]，这也为稳压器的模型辨识带来了许多阻碍。在过去的几十年里，陆续涌现了许多相关的辨识方法，并逐渐形成了使用带噪声的观测数据对模型的未知参数实现建模优化的形式[2]，比如递推最小二乘法[3,4]、人工神经网络[5]、常微分方程法[6]、以及在输出信号加以处理后建立基于偏差补偿系统的建模方法。这些方法虽然能实现模型的辨识，但需要外加测试信号，势必对原模型造成干扰，导致过程输出超出约束范围。本文提到的闭环辨识方法[7]，不用额外加入测试信号，只要系统能够稳定运行，通过系统的输入、输出数据就可以将模型辨识出来。

1 稳压器系统

1.1 稳压器工作原理

压水堆核电站中稳压器在一回路的具体位置[8]如图1所示。

图1 压水堆核电站工艺流程图

一回路中设备的压力由稳压器内的蒸汽压力来表示。稳压器的功能主要是调节整个系统中冷凝剂的压力,确保核电站在稳定运行时整个回路中的压力值在设定值附近浮动,防止回路中因为压力太高致使核电厂设备损坏,或者压力太低导致稳压器中液体沸腾,致使反应堆堆芯散热故障，发生重大安全事故[9]；当稳压器的压力值大于预先设定的值，系统将会自动将安全阀门打开，使稳压器内的压力值降低，使其稳定在安全阈值内。稳压器的控制系统由两个独立的控制系统组成。系统的压力主要由喷淋阀加热器以及气体释放阀来控制。当系统正常稳定运作时,稳压器中的液体与气体维持在某个平衡状态。当喷淋阀中喷淋出冷水时,稳压器上方的蒸汽因为喷淋的冷水而凝结成液体，沿着稳压器内壁向下流入液体部分,稳压器内蒸汽的压力由此减小;而当加热器工作后,稳压器下方液体空间的部分液体受热变为蒸汽蒸发到稳压器内部上方的蒸汽空间,此时稳压器内的压力上升。而稳压器液位则主要由上充阀门和下泻阀门开合度来控制。

1.2 稳压器耦合被控对象简化模型

将该系统简化为双输入双输出模型[10]，搭建稳压器耦合控制系统的数学模型如图2所示，两个输出变量是：上充阀门和下泄阀门的流量差值、电加热器的功率值。通常假设下泄阀门的值保持不变，那么电加热器功率值、上充阀的流量即为系统的两个输入变量，而系统的输出变量则分别是稳压器的压力与水位。

图2 稳压器的数学模型结构图

稳压器压力降低时，电加热器会加大功率，使稳压器内的水受热蒸发为水蒸汽，增加稳压器内部蒸汽部分的压力。相反，压力过高时，加热器功率降低，喷淋阀的喷淋量会增加，促使稳压器内部的蒸汽凝结成水，降低稳压器内的压力值；当稳压器内的水位出现偏差时，稳压器会及时地调整上充阀门和下泄阀门的流量，确保水位在阈值范围内。

2 多变量过程模型辨识方法

2.1 过程对象频率响应矩阵

假设一个n输入n输出的多输入多输出系统，如图3所示，图中ri(i=1,2,…,n)是系统设定值，ui(i=1,2,…,n)是控制量，yi(i=1,2,…,n)是被控变量，K(s)、G(s)分别为控制器和被控对象。

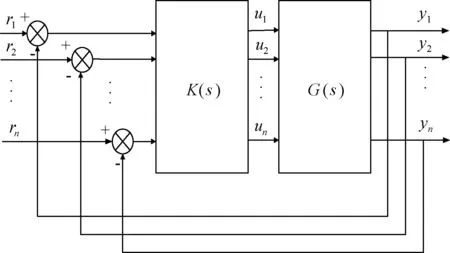
图3 多变量控制系统框图

(1)

当系统设定值ri发生变化时, 那么被控量yi和控制量ui都会从之前已经稳定的状态逐渐过渡，达到新的稳态。这些信号都可分解为

yi(t)=Δyi(t)+ysi

(2)

ui(t)=Δui(t)+usi

(3)

式中: Δyi(t),ysi与Δui(t)，usi分别为yi和ui的瞬态及稳态部分。假设设定值r1先发生变化,并维持其它值不变;记录所有控制量ui(t)和被控量yi(t)的变化过程,直到它们达到新的稳态状态。这样,Y1(s)和U1(s)满足如下关系：

Y1(s)=G(s)U1(s)

(4)

接着改变设定值r2，并保持其余设定值不变，重复前面步骤，直至n个设定值全部发生变化，即可得到下面的表达式：

[Y1(s)，…，Yn(s)]=G(s)[U1(s)，…，Un(s)

(5)

由于Uk(s)(k=1,2,…,n)线性无关，所以传递函数G(s)可以表示为：

G(s)=[Y1(s)，…，Yn(s)]×

[U1(s)，…，Un(s)]-1

(6)

经过拉氏变换、替换和化简，用jω替换式(6)中的s，可以得到G(jω)表达式。

2.2 传递函数矩阵模型

由多变量过程对象的频率响应，可以得到传递函数矩阵中的各个元素，传递函数矩阵中的每个元素采用二阶加纯滞后模型：

(7)

式中：系数a,b,c以及L的值可由下列表达式计算得出：

|G(jωl)|2c2=1

(8)

(9)

将式(8)(9)改写成矩阵形式，即：

φθ=Γ

(10)

其中

式中：θ可以通过最小二乘法得到，即

θ=(φTφ)-1φTΓ

(11)

那么模型的参数就可以从θ中获得

(12)

上文提到的辨识方法能够用于多输入、多输出系统的PID控制以及复杂控制系统解耦控制中，并达到很好的效果。在系统里，系统的输入、输出变量一一对应。该辨识方法也能在预测控制系统中使用，输入输出变量根据个数不同可以分为不同的系统。如果输入变量的个数少而输出变量的个数多时，此时系统成为瘦系统，系统已知的数目将比控制变量的个数多，改变已知量能确保变量Uk(s)(k=1,2,…,n)不是线性相关的，则该变量组成的矩阵一定是可逆的；而当控制变量的个数大于已知数目，系统变为胖系统，变量Uk(s) 的相关性就不能确定，则由Uk(s)组成的矩阵是否可逆便不确定。但是在现场，对于胖系统而言，控制系统的预测通常是将多余控制量的值保持固定为最优解，则已知数目等于控制变量的个数，也可将其视为瘦系统，符合本文使用该辨识方法的前提。

3 模型辨识验证

模型辨识精度可以由辨识误差来量化：

(13)

为了验证本文中提到的方法的可行性，引入一压水堆核电站稳压器的数学模型[11]加以验证。一压水堆核电站稳压器的数学模型传递函数如下：

辨识结果显示其参数误差E=4.1%。

本文中提到的方法在稳压器系统辨识中有很好的辨识度，利用这种辨识方法得出的模型能直接用于多变量控制器的设计，比如稳压器模型的解耦控制器设计等。

4 结论

本文针对稳压器模型辨识中耦合系统辨识精度低，鲁棒性不高的问题，引入了一种多变量过程闭环辨识方法。首先得到稳压器的水位和压力的被控特性，并搭建耦合数学模型，通过对运行中的系统产生的信号加以频谱分析，获得稳压器模型的频谱响应矩阵，最终通过递推最小二乘法拟合出系统参数。实验表明，这种方法能有效的辨识出稳压器的模型，在工程上具有可行性，为核电站的控制仿真提供了便利，提高了运行的安全性。

参考文献：

[1] 钱虹,周蕾,房振鲁.压水堆核电站稳压器压力和水位的解耦控制研究[J].核科学与工程,2017,37(1):5-11.

[2] 毛晓芳,侯力,马登秋,等.燃气轮机载荷动力系统优化建模仿真[J].计算机仿真,2017,34(10):49-54.

[3] 张海宁.基于递推最小二乘算法的逆变器参数辨识[J].电力科学与工程,2017,33(2):21-27.

[4] 丁锋,汪菲菲.损失数据线性参数系统的递推最小二乘辨识方法[J].控制与决策,2016,31(12):2261-2266.

[5] 苏一新,马彦会,石倩,等.基于BP神经网络模型的磁悬浮水泵PID参数优化[J].流体机械,2018,46(1):20-24.

[6] 邱舒婷,张志祥.解常微分方程程序的蜕变测试方法[J].舰船电子工程,2016,36(12):29-33.

[7] 王亚刚,许晓鸣.复杂多变量过程模型的闭环频域辨识[J].控制与决策,2010,25(6):825-830.

[8] 马进,刘长良,李淑娜.稳压器压力水位控制系统建模与仿真[J].核科学与工程,2010,30(1):9-14.

[9] 许志斌. 核电站稳压器机理建模分析及控制研究[D].广州:华南理工大学,2016.

[10] 董化平,张倬,孙启航,等.压水堆核电厂稳压器压力和水位控制系统仿真研究[J].自动化与仪器仪表,2017(1):138-141.

[11] 张国铎. 基于智能控制理论的压水堆稳压器控制系统的研究[D].上海:上海电力学院,2013.