基于公平性约束的无线体域网集中式调度算法*
2018-06-05谢志军石守东
经 贞, 谢志军, 石守东, 纽 俊
0 引 言
无线体域网络(wireless body area network,WBAN)是控制器Sink节点和附着在人体或植入体内的小的传感器节点组成的无线网络[1],WBAN中的节点通常靠电池供电,一些植入体内的传感器节点电池难以更换。传输调度在资源受限的条件下传输调度是优化WBAN性能的一种重要方法。
传输调度方法分为集中式和分布式两种。集中式方法收集整个网络的信息,在Sink节点处统一调度。文献[2]将最优的节点调度问题定义为在一定性能指标下随机控制问题,并用动态规划求解。文献[3]将近似最优的节点能量管理算法引入部分可观察马尔科夫模型和多臂赌博机模型。文献[4]采用层层迭代的方法,通过寻找帕累托最优来最大化网络生存期。分布式方法由各节点根据自身的信息判断下一时隙是否传输数据。文献[5]总结出无线传感网络生存期的一般公式。文献[6]根据文献[5]的生存期标准,提出了最大化生存期的动态协议(dynamic protocol for lifetime maximization,DPLM),基本思想为调度算法选择激活节点中当前链路质量所需的传输能量占剩余能量的比例最小的节点。在节点数量有限的WBAN中,集中式调度能以较小代价获得网络生存期的全局最优值。
上述传输调度算法均未考虑WBAN所监测不同的生理信号有不同的数据传输需求,单纯以网络生存期为优化目标建立模型,会使个别传感器节点长期饥饿。对此,文献[7,8]从介质访问控制(media access control,MAC)层协议的角度设计公平性策略。文献[9,10]将网络中传输的数据分为紧急数据和一般数据,从数据优先级的角度设计公平性策略。文献[11]通过引入谈判层来平衡系统的吞吐量和公平性。
本文借鉴了文献[3]的建模方法和文献[11]的公平性设计思想,将WBAN的传输调度问题建模成一个包含公平性参数的受限的马尔科夫决策过程,并利用动态规划思想进行求解。
1 模型描述
模型中的向量用粗体表示,变量用斜体表示。1[x]表示当x为真时,l[x]=1;当x为假时,1[x]=0。所用到的符号列举如下:N为节点数量;ε0为节点初始能量;Wn为当节点n被调度时,成功将一个数据包传输到Sink节点需要的能量;En为节点N在数据传输前剩余能量;εk为节点传输数据包的功率等级;W=(W1,…,WN)为网络传输所需的能量;E=(E1,…,EN)为网络剩余能量。
1.1 能量模型
节点n成功传输一个数据包所需的能量Wn是一个随机变量,与信道状况有关。信道状态越好,传输所需的能量越小。由于硬件电路限制,Wn被限制在一个有限的集合ω中,ω定义为
ω
(1)
节点n的剩余能量En为一个随机变量,与信道状况和网络的调度策略有关。剩余能量En从有限集ε中取值
ε
(2)
1.2 生存期定义
依据数据传输时隙开始时所需的传输能量Wn和剩余能量En的定义,节点n有以下几个状态:
激活态:在当前时隙有足够的能量传输En≥Wn
非激活态:较最小传输能量高,但低于当前信道所需的传输能量ε1≤En≤Wn
死亡态:剩余能量降低到传输能量的最小要求,即En≤ε1。说明无论在任何链路状况下,节点均没有足够的能量传输。
文献[12]将传感器网络生存期定义为当网络中死亡节点达到阈值NT时所收集到的数据包的数量。其中
NT=N-N0+1
(3)
式中N0为每个时隙调度节点的数量。本文设NT=1,即生存期定义为网络中第一个节点死亡时收集的数据包数。
1.3 公平性定义
文献[13]中的公平性指数已经广泛应用在网络公平性测评上,当有M个激活态节点竞争时,节点i所接收到的归一化的时间分配表示为
(4)
式中Ti为节点i的实际传输时间;O为总的传输时间;bi为权值,表示节点i的重要程度。
每个时隙的公平性指数可以描述为

(5)
当f=1为完全公平,值越大,公平性越高。
1.4 优化目标
调度算法每个时隙动态选择一个节点进行传输,在公平性约束下最大化网络生存期。已知所有传感器节点的瞬时信道信息,即传输能量需求W=w和剩余能量E=e。假设w和e是某个数据传输时隙下的传输能量和剩余能量值,传输调度算法选择节点编号a的条件可表示为
a=μ(e,w,f)μ:εN×ωN→{1,…,N}
(6)
2 模型建立
一个马尔科夫决策过程可以定义成一个五元组
将整个网络的传输能量,剩余能量和公平性权值作为一个马尔科夫状态。算法以1的概率在终态下终止,通过随机动态规划的值迭代算法求解模型。目标为当系统达到终态时,在保证一定公平性的前提下,最大化整体回报。
2.1 状态空间
网络的状态空间S定义为
S{i=(e,w,f):e∈εN,w∈ωN}
(7)
WBAN的终止状态St定义为St⊂S
St{(e,w,f):|en:en<εl|≥NT或e (8) 动作序列表示为集合A,状态i=(e,w,f)∈S下的动作集合定义为 A(i)=A[(e,w,f)]{n:en≥wn} (9) (10) 式中pw(w′)=Pr{W=w′}为W的概率密度函数,在给定的传输能量等级w′上取值,由当前链路状况决定。 进入终态之前,每个传输时隙WBAN会获得一个单位的回报。网络生存期为进入终态前每个时隙获得立即回报的总和。假设当前网络状态为i=(e,w,f),定义立即回报函数 R(i)1i∈t (11) 状态i下的动作集合A(i)中,动作需满足公平性条件才被称给可行性动作,即当执行完该动作后,网络的公平性指数f较给定的公平阈值fn要大。F(i,a)表示在状态i下执行完动作a后的下一个状态的公平性指数,可行性动作需满足 f(i,a)≥fn (12) 将状态i下所有可行性动作定义为集合Aa(i)。 将WBAN中的节点调度问题定义为一个受限的马尔科夫决策问题,调度算法即为该问题的一个策略集π,由一系列动作组成。π={μ1,μ2,…},其中μl定义为状态集S到选择调度的节点编号的映射,即μl:S→{1,2,…,N},N表示在第l个时隙所选择的节点编号。用Lπ(i)表示状态i下采用策略集π所得到的网络生存时间,即累计回报。最大的网络生存时间L*(i)表示为 (13) 获得L*(i)的策略π*称为最优策略,在非终结状态SSt实现了最大化的网络生存时间。表示为 Lπ*(i)=L*(i),∀i∈SSt (14) 受限的马尔科夫决策过程的最优解π*即为节点调度问题的解。 上述模型可以用图1简单示意,假设WBAN中有2个节点,初始化能量均为ε0。 图1 2个节点的算法举例 从状态i开始,运用公平性约束,最大化期望的网络生存期L*(i)可以通过贝尔曼最优等式获得最优解[14]。 L*(i)=L*[(e,w,f)]= ∀i∈S,s.t.fj≥fn (15) 式中fj为WBAN在状态j的公平性指数,fn为不同应用场景所特定的公平性阈值。具体求解过程参考文献[15]。 对于所有i∈S初始化L0(i)=0。因为终态是吸收态,回报为0,从终态开始的最大生命期是0,即表示为 L*(i)=0,i∈St (16) 最优策略μ可表示为 (17) 调度算法具体实现方法如下: 1)每个时隙开始时,Sink节点广播一个数据包激活网络中的所有节点; 2)每个节点收到后,发送数据包给Sink节点,使Sink节点获得网络各节点的链路质量信息; 3)Sink节点评估所有响应节点的信道状况,调用功率控制算法,计算出传输所需的能量w; 4)Sink节点根据当前网络状态(e,w,f)和上述调度算法计算出的最优策略 ,决定调度节点的标号; 5)Sink节点广播调度节点ID和所需的传输功率等级; 6)调度的节点按收到的传输功率等级将观测值传输给Sink节点。 仿真实验采用Omnet++中的MiXiM框架。实验中设计的一个Sink节点和6个传感器节点,具体如图2所示。 图2 仿真实验节点部署 数据传输使用2.4 GHz的射频频段,仿真时间为2 000 s。具体的仿真参数设计:载波频率为2.4 GHz,网络为星型拓扑,同步模式为信标,传输/接收功率为1 mW,睡眠能耗为0.02 mW,唤醒能耗为1.5 mW,数据传输速率为250 kbps,队列长度为10个包,MAC载荷大小为50 B,终端数量为6。 将改进后的算法与WBAN中常见的调度算法在网络生存期这一指标进行对比。分别与随机调度算法、机会调度算法、保守算法和DPLM比较。 1)比较不考虑公平性阈值时几种方法在网络生存期上的差别。能量等级L=6,传输所需的能量等级 ,转移概率即信道分布定义pwn(1)=pwn(2)=pwn(3)=pwn(4)=1/8,pwn(5)=pwn(6)=1/4。图3给出了算法的节点初始能量和网络生存期的关系,可以看出:随机调度算法的网络生存期最短。在初始能量较小时,保守算法的网络生存期优于机会调度算法。因为在网络能量相对较小时,剩余能量相比链路质量这一因素更易使节点死亡。本文提出的算法由于考虑整个网络的链路质量,在生存期上达到最优值。 图3 不考虑公平性阈值的生存期比较 2)考虑公平性阈值对模型在网络生存期上的影响。公平性阈值根据不同应用场景的要求,分别设为0.2,0.4,0.6和0.8。节点权值相同和权值不同2种情况的网络生存期如图4所示。权值相同时,各节点均设为1/6。权值不同时,各节点权值设为0.5,0.3,0.1,0.05,0.04和0.01。可以看出,当权值相同时,随着公平性阈值的增大,网络的生存期亦越来越大。但当公平性阈值达到一定值,如fn=0.8时,过高的公平性反而限制网络的生存期。因此,合理选择公平性阈值可以延长网络生存期。对比图4的2条曲线可看出:公平性阈值较低时权值因素对生存期的影响不大,权值不同时公平性阈值的差异对网络的生存期影响更为明显。可见,该算法对公平性不同的场景更为敏感,适用于监控不同生理信息的WBAN这一应用场景。 图4 不同公平性阈值的生存期比较 将基于全局链路信息的WBAN调度过程建模成一个公平性约束下的马尔科夫决策过程,提出了一种WBAN集中调度算法。通过实验证明:在不考虑公平性阈值时,该算法在网络生存期上优于传统调度方法。公平性阈值在一定范围内时能够提高网络生存期,节点权值不同时公平性阈值对生存期的影响更加明显。因此,应根据实际应用背景合理调整节点权值和网络公平性阈值,为今后研究的方向。 参考文献: [1] 邓世洲,高伟东,胡 炜,等.无线体域网技术研究现状与展望[J].传感器与微系统,2014,33(11):1-4. [2] Krishnamurthy V.Algorithms for optimal scheduling and management of hidden Markov model sensors[J].IEEE Transactions on Signal Processing,2002,50(6):1382-1397. [3] Chen Y,Zhao Q,Krishnamurthy V,et al.Transmission scheduling for optimizing sensor network lifetime:A stochastic shortest path approach[J].IEEE Transactions on Signal Processing,2007,55(5):2294-2309. [4] Dagher J C,Marcellin M W,Neifeld M A.A theory for maximizing the lifetime of sensor networks[J].IEEE Transactions on Communications,2007,55(2):323-332. [5] Chen Y,Zhao Q.On the lifetime of wireless sensor networks[J].IEEE Communications Letters,2005,9(11):976-978. [6] Chen Y,Zhao Q.An integrated approach to energy-aware medium access for wireless sensor networks[J].IEEE Transactions on Signal Processing,2007,55(7):3429-3444. [7] Choi J S,Kim J G.An improved MAC protocol for WBAN through modified frame structure[J].International Journal of Smart Home,2014,8(2):65-76. [8] Gündogˇdu K,Çalhan A.An implementation of wireless body area networks for improving priority data transmission delay[J].Journal of Medical Systems,2016,40(3):1-7. [9] Kim R H,Kim J G,Seo B W.Channel access with priority for urgent data in medical wireless body sensor networks[J].International Journal of Applied Engineering Research,2016,11(2):1162-1166. [10] Kim R H,Kim J G.Adaptive MAC protocol for emergency data transmission in wireless body sensor networks[J].International Journal of Software Engineering and Its Applications,2015,9(9):205-216. [11] Cheng H T,Zhuang W.An optimization framework for balancing throughput and fairness in wireless networks with QoS support[J].IEEE Transactions on Wireless Communications,2008,7(2):584-593. [12] Yun Y S,Xia Y.Maximizing the lifetime of wireless sensor networks with mobile sink in delay-tolerant applications[J].IEEE Transactions on Mobile Computing,2010,9(9):1308-1318. [13] Wang Z,Yu F,Tian J,et al.A fairness adaptive TDMA scheduling algorithm for wireless sensor networks with unreliable links[J].International Journal of Communication Systems,2014,27(10):1535-1552. [14] 肖 华.无线通信中的马尔科夫决策过程研究[D].成都:电子科技大学,2013. [15] Lovejoy W S.A survey of algorithmic methods for partially observed Markov decision processes[J].Annals of Operations Research,1991,28(1):47-65.2.2 动作空间
2.3 转移概率
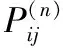
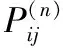
2.4 传输回报
2.5 公平性约束
2.6 受限的马尔科夫决策问题
2.7 举 例
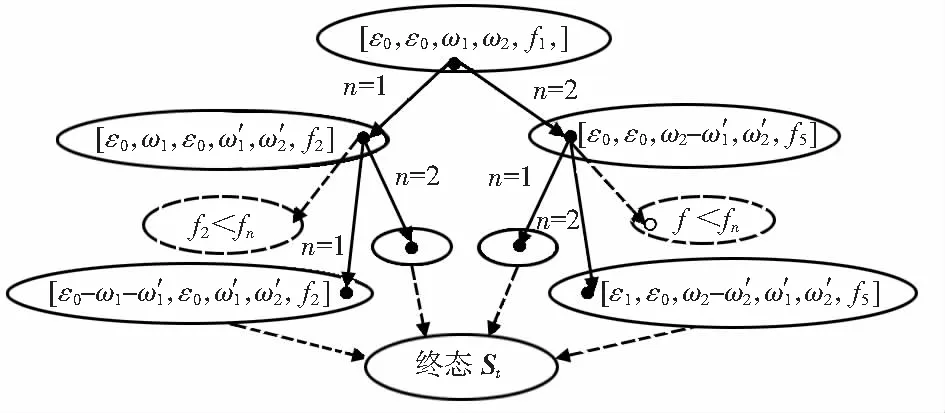
2.8 最优策略

2.9 算法实现
3 仿真实验
3.1 实验环境和参数设计
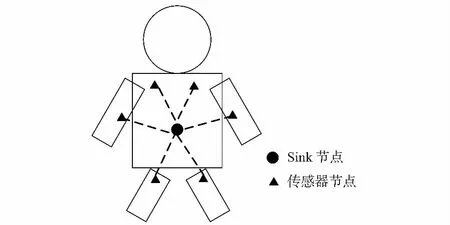
3.2 实验结果与分析


4 结 论
