OQAM/OFDM系统中基于LMMSE的时域信道估计方法*

薛伦生， 陈 航， 邱上飞

0 引 言

近年来，偏移正交幅度调制的正交频分复用(offset quadrature amplitude modulation/orthogonal frequency division multiplexing，OQAM/OFDM)技术由于其高频谱利用率和低带外辐射受到广泛的关注[1～3]。相比于OFDM技术，其不需要插入循环前缀(cyclic prefix，CP)或其他保护间隔，有效提高系统的频谱利用率；同时其引入具有良好时频聚焦特性的滤波器，可以有效降低带外辐射和抵抗信道造成的符号间干扰(inter-symbol interference,ISI)和载波间干扰(inter-carrier interference,ICI)。但同时，原型滤波器的使用放宽了正交条件，OQAM/OFDM系统仅在实数域满足正交，使系统在传输符号时不可避免地引入虚部干扰，信道估计成为其面临的困难。大量文献对OQAM/OFDM系统信道估计进行研究[4～9]。但所有方法均在信道的延迟扩展远小于系统的符号时间间隔的假设之下开展，当信道为高频率选择性信道时，这个假设将不成立。此时，在高信噪比(signal-to-noise ratio，SNR)情况下系统将存在严重的“误码平层”现象，系统的信道估计性能出现严重下降。针对这种情况，文献[10]提出一种基于时域的信道估计方法，通过使用频域的导频符号在时域估计信道的脉冲响应。在时域信道估计模型中，不需要假设信道的延迟小于符号时间间隔，可以有效消除“误码平层”现象。文献[11]提出了基于多重信号分类(multiple signal classification,MUSIC)和最小二乘(least squares,LS)算法的时域信道估计方法,但其必须要求导频符号在奇数和偶数子载波上相等。文献[12]提出了在时域信道的加权最小二乘(weighted least squares,WLS)估计和线性最小均方误差(linear minimum mean square error,LMMSE)估计方法，前者将信道噪声协方差矩阵加入LS中提高信道估计性能；后者需要信道协方差信息，得到更好的信道估计性能，但在现实中信道协方差信息很难得到。

通过建立时域信道模型，本文提出一种不需要了解信道协方差矩阵信息的时域LMMSE信道估计方法。通过设置初始信道协方差，利用迭代的方法对信道协方差矩阵进行估计。仿真结果表明，该方法有效地克服了频域信道估计存在的“误码平层”现象，比文献[12]提出的WLS信道估计方法有更好的性能，接近于其提出的LMMSE信道估计性能。

1 OQAM/OFDM系统时域信道估计模型

OQAM/OFDM系统模型如图1所示，发送端发送的符号为

(1)

式中g(t)为成型滤波器的基函数；gm,n(t)为在时频坐标点(m,n)的滤波器；am,n为第m个子载波上发送的第n个符号；v0和τ0分别为OQAM/OFDM系统子载波间隔和发送符号间隔，且v0=1/2τ0。

图1 OQAM/OFDM系统模型

假设信道为无失真信道，当满足如下正交条件时可以完美地重构信号am,n

〈gm,n,gp,q〉R=δm,pδn,q

(2)

当m=p时，δm,p=1；当m≠p时，δm,p=0。

定义

(3)

发送信号经过信道脉冲响应为h(t,l)的多径信道后，在接收端收到的信号为

r(t)=h(t,l)*s(t)+η(t)

(4)

η(t)为均值为0方差为σ2的高斯白噪声。在时频格点(p,q)处解调信号可得

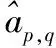
(5)

将式(1)，式(4)代入式(5)可得

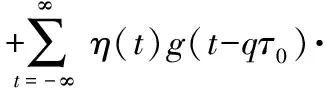
(6)

在帧结构的数据传输过程中，考虑在第一列加入导频符号，为了消除ISI，在导频符号右侧加入保护间隔。文献[12]指出，在时频聚焦特性良好的滤波器中，加入的保护间隔越多，ISI的影响越小。当加入三列保护符号后，ISI的影响可以忽略不计。

加入保护间隔后，假设符号间干扰为0，则在接收端导频符号可以表示为

(7)

令

e-j2πmv0l

(8)

(9)

则式(6)表示为矩阵形式

a0=Θh+η0

(10)

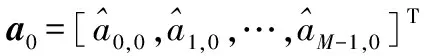
对均值为0，方差为σ2服从正态分布的高斯白噪声ηp,0，(p1,p2)两处导频的协方差为

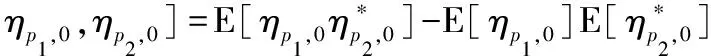
(11)

可以看出，与OFDM系统信道噪声不相关不同,在任意两处导频处噪声具有相关性，这是由于OQAM/OFDM系统存在虚部干扰,因此,导频列的协方差矩阵可以表示为

(12)

因此OQAM/OFDM系统的时域信道模型为扩展线性模型，由传统的LS信道估计方法可得信道脉冲响应为

(13)

2 时域LMMSE信道估计方法

由式(13)可以看出，传统的LS信道估计方法忽略了噪声的影响，信道估计的性能较差。文献[12]中提出一种WLS信道估计和LMMSE信道估计，前者加入信道噪声协方差矩阵，但并不知道信道信息，后者通过加入噪声协方差矩阵和信道协方差矩阵进行准确的信道估计，但在实际的信道中，信道协方差矩阵很难预先了解，因此,本文提出一种不需要信道协方差矩阵的LMMSE信道估计方法。

传统的LMMSE信道估计方法为

(14)

式中Rhh为信道协方差矩阵。在实际信道中，Rhh很难知道，因此,本文提出一种迭代的方法估计信道协方差矩阵。

(15)

将LS信道估计得到的信道协方差矩阵作为迭代的初始值，则式(14)可以改写为

(16)

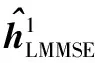
(17)

2)通过LMMSE信道估计方法求信道脉冲响应。

3)计算信道协方差矩阵。

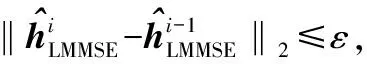
5)更新信道协方差矩阵，返回步骤(2)。

3 仿真结果及分析

为验证本文所提方法的性能，对所提方法与文献[12，15]中所提方法进行对比分析。仿真参数设置如下：OQAM/OFDM系统子载波数为256，采用4-QAM方法调制，滤波器使用IOTA滤波器，抽头数为4，导频结构如图1所示。信道采用多径功率服从负指数分布的瑞利多径衰落信道γ(l)=e-0.5l，l=1,2,…lh，本文选用lh=6和lh=202种多径数分别代表低频率选择性衰落信道和高频率选择性衰落信道。采用归一化均方误差(normalized mean square error，NMSE)反映信道估计性能

NMSE=E{‖H-‖2/‖H‖2}

(18)

图2为lh=20和lh=6 2种多径情况下时域和频域信道估计NMSE性能。F-LS和F-LMMSE为文献[15]的OQAM/OFDM系统频域信道估计方法，T-LS和T-LMMSE分别为文献[12]提到的时域信道估计方法。可以看出，在高频率选择性衰落信道下，频域信道估计方法存在严重的误码平层现象。图2(a)中误码平层比图2(b)所示的低频率选择性衰落信道严重，这是由于信道延迟扩展小于符号间隔的假设不再成立。从图中可以看出，时域信道估计的方法不存在误码平层的现象，且信道估计性能远好于频域信道估计方法。

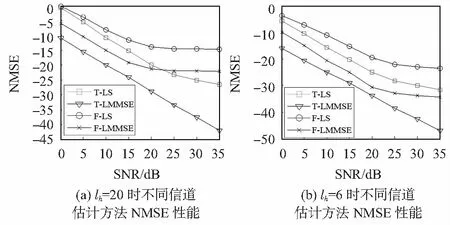
图2 2种情况下信道估计

图3为本文方法与文献[12]中所提的时域信道估计方法在不同的衰落信道下性能比较。图中T-LMMSE-n为第n次迭代得到的LMMSE信道估计方法NMSE性能，T-WLS为文献[12]提出的加权LS时域信道估计方法。n=1时为本文所提方法即为LS信道估计方法;当n=2时本文所提的方法已经优于WLS信道估计方法;当n=3时本文所提方法与文献[12]的已经预先知道信道协方差矩阵信息的LMMSE信道估计方法有相近的信道估计性能，比WLS信道估计方法有5 dB的性能提升。

从图中可以看出，本文所提方法在2次迭代后就能得到由WLS信道估计方法的性能，在3次迭代后能够得到与已知信道协方差矩阵的LMMSE信道估计方法相近的性能。因此，在了解信道协方差矩阵的情况下本文所提方法比WLS方法具有更好的信道估计性能。

4 结 论

本文提出了一种时域的迭代LMMSE信道估计方法。通过仿真分析可以看出，本文所提的方法可以消除频域信道估计方法存在的误码平层现象，同时能够得到与已知信道协方差矩阵的LMMSE信道估计方法相近的信道估计性能。

参考文献:

[1] Farhang-Boroujeny B.Filter bank spectrum sensing for cognitive radios[J].IEEE Transactions on Signal Processing,2008,56(5):1801-1811.

[2] Saeedi-Sourck H,Wu Y,Bergmans J W M,et al.Complexity and performance comparison of filter bank multicarrier and OFDM in uplink of multicarrier multiple access networks[J].IEEE Transactions on Signal Processing,2011,59(4):1907-1921.

[3] Baig S,Mughal M J.Multirate signal processing techniques for high-speed communication over power lines[J].IEEE Communications Magazine,2009,47(1):70-79.

[4] Lélé C.Iterative scattered-based channel estimation method for OFDM/OQAM[J].EURASIP Journal on Advances in Signal Processing,2012,2012(1):1-14.

[5] Fuhrwerk M,Moghaddamnia S,Peissig J.Scattered pilot based channel estimation for channel adaptive FBMC-OQAM systems[J].IEEE Transactions on Wireless Communications,2017,16(3):1687-1702.

[6] Cui W,Qu D,Jiang T,et al.Coded auxiliary pilots for channel estimation in FBMC-OQAM systems[J].IEEE Transactions on Vehicular Technology,2016,65(5):2936-2946.

[7] Kofidis E,Katselis D,Rontogiannis A,et al.Preamble-based channel estimation in OFDMOQAM systems:A review[J].Signal Processing,2013,93(7):2038-2054.

[8] Guobing C,Yue X,Su H,et al.Interference cancellation aided channel estimation for OFDM/OQAM system[J].Science China,2013,56(12):1-8.

[9] Hu S,Wu G,Yang G,et al.Effectiveness of preamble based channel estimation for OFDM/OQAM System[C]∥International Conference on Networks Security,Wireless Communications and Trusted Computing,IEEE Computer Society,2009:34-37.

[10] Kofidis E,Katselis D,Rontogiannis A,et al.Preamble-based channel estimation in OFDM/OQAM systems:A review[J].Signal Processing,2013,93(7):2038-2054.

[11] Garbo G,Mangione S,Maniscalco V.MUSIC-LS modal channel estimation for an OFDM-OQAM system[C]∥International Conference on Signal Processing and Communication Systems,IEEE,2009:1-8.

[12] Kong D,Qu D,Jiang T.Time domain channel estimation for OQAM-OFDM systems:Algorithms and performance bounds[J].IEEE Transactions on Signal Processing,2014,62(2):322-330.

[13] Savaux V,Bader F,Louet Y.A joint MMSE channel and noise variance estimation for OFDM-OQAM modulation[J].IEEE Transactions on Communications,2015,63(11):4254-4266.

[14] Savaux V,Louet Y,Bader F.Low-complexity approximations for LMMSE channel estimation in OFDM/OQAM[C]∥International Conference on Tele-communications,IEEE,2016:1-5.

[15] Savaux V,Bader F.Mean square error analysis and linear minimum mean square error application for preamble-based channel estimation in orthogonal frequency division multiplexing/offset quadrature amplitude modulation systems[J].IET Communications,2015,9(14):1763-1773.