基于有限元的拉丝机机架的优化分析
2018-06-05黄仲勇
黄仲勇
基于有限元的拉丝机机架的优化分析
黄仲勇
(四川省机械研究设计院,四川 成都 610063)
拉丝机是利用金属丝拉拔过程在拉丝模内产生的弹性变形与塑性变形实现金属丝尺寸及物理特性改变的机械设备,其中机架的强度会直接影响拉丝机的生产效率,目前基本都是采用经验来设计与制造。在对拉丝机机架进行深入分析的基础上,结合机架实际受力特点及设计现状,分析拉丝机机架的受力情形后对其进行几何简化,并进行四面体网格划分,采用拓扑优化分析拉丝机机架,根据机架的拓扑优化分析过程、结果及对原模型进行改进,以达到保证强度、优化结构的目的。
拉丝机;机架;拓扑优化分析
随着金属制品行业技术的不断发展,对拉丝产品质量的要求不断提高[1]。国内厂家对拉丝机机架方面的优化设计多是凭借设计者的经验,所以很有必要对机架进行优化分析。机架必须满足工况、强度、刚度、美观、稳定性等的要求,目前国内产品在以上方面已能完全满足用户要求,稳定性甚至超过了同机型的国外拉丝机,现在需要做的是合理布置机架结构形式,减少材料使用,并进一步提高刚度。
1 机架的受力及设计特点
拉丝机机架是为卷筒、减速器及电机提供支撑,安装布置位置如图1所示。卷筒安装在机架上,除防护罩外几乎不受其他载荷的作用,卷筒的传动链将自重较大的部件放置于机架底部,使重心下移,提高了整机的稳定性。另外,机架的高度较低,对稳定性也有帮助。

图1 机架上的布置
拉丝机机架设计采用以桁架结构为主并结合板结构的形式。机架采用的矩形钢管规格为100 mm×100 mm、200 mm×100 mm、300 mm×200 mm,重要区域如支撑卷筒及减速器所用的钢板厚度为30 mm,非重要区域如两侧钢板厚度为10~12 mm。机架自重为0.7~1 t。
2 机架的受力变形分析
有限元分析中需去除一些不必要的细节,突出机架的受力本质;同时为便于划分网格也需要简化几何模型,如忽略细小的圆角等。图2(a)为拉丝机机架的三维几何模型,分析受力情形后对其进行几何简化,如图2(b)所示。

图2 机架的三维几何模型
模型简化后需进行网格划分。因所用材料为板材、型材,所以可将其视作壳体,但这仅限于模型比较简单的情形。本例中机架构造复杂,尤其为加强刚度,在板壳之间有大量通过焊接实现的重叠。在有限元分析时重叠部分往往很难处理,大量网格节点需要手动对齐使其重合。因此在分析中将采用实体网格,可以将机架的各个板块合并成一个,然后再划分网格。本次分析中采用四节点线性四面体单元,这样可以减少占用计算机资源,为确保精度可以适当加密网格。分析采用的有限元模型如图3所示,整个模型共划分507098个单元。

图3 机架的有限元模型
图4为施加载荷的示意图,其中,第一、二道次卷筒及减速器重量为1869 kg,最后道次的重量为2384 kg。电机重量按400 kg计算。所有集中力均施加在耦合约束的参考点上。

图4 机架的边界条件施加
分析得到机架变形及应力如图5所示。最大变形量为0.0887 mm,出现在第三道次靠后部。最大应力为34.45 MPa,出现在第三道次机架后部的支柱下部。由于第三道次的卷筒需要积线较多,其构造与前两道次不同,表现在自重的增大,因此最大变形出现在第三道次的钢板上。又根据应力云图,机架上支撑整体重量的是八根矩形钢管支腿,应力在支腿处比其他部位大;又由于第三道次受力较大,其后部支腿处的应力在整个模型中最大。由于还有电机自重,因此无论是最大变形还是最大应力均出现在机架靠后部位。另外,图中机架下方的两根焊接在机架上的电缆管、回水管对提高机架的刚度并无太大帮助。
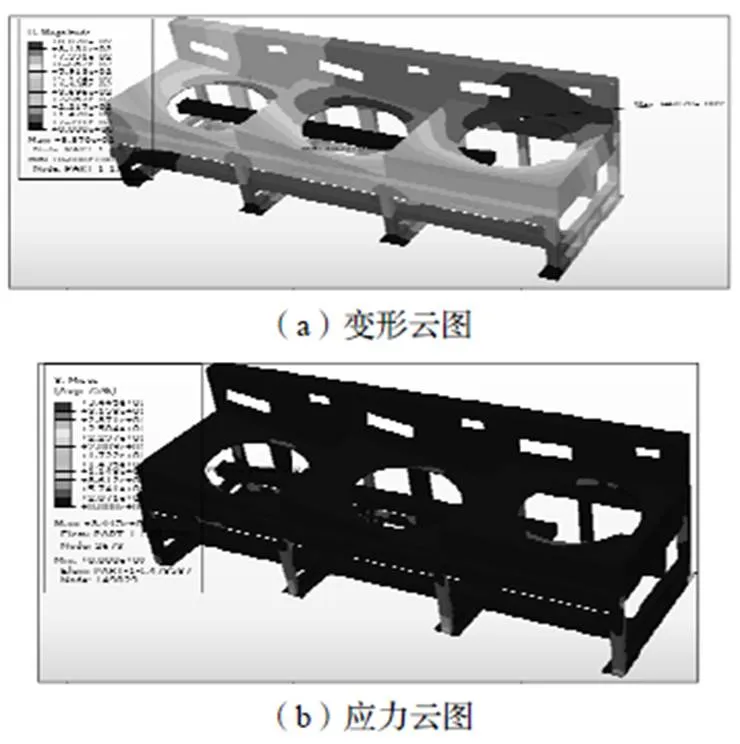
图5 机架的有限元分析结果
3 机架的拓扑优化分析过程、结果及对原模型的改进
本文优化的对象是LZ900拉丝机机架,此前设计采用经验方法,带来的问题是某些位置刚度较好却使用较多的材料、而某些位置刚度较差却用了较少的材料。根据已有的机架结构,其后部需要安装电机,因此后部矩形钢管不能移除,另外机架上部为采用20~30 mm厚的钢板焊接的壳体,用于安装卷筒及减速器,由于壳体很薄因此没有进一步优化的必要。制造机架的所有零部件均通过焊接组合在一起。
在优化分析前,首先要建立基结构模型。基结构即为初始结构,若直接在原来机架的模型上分析优化则相当于已打上了原始模型的烙印,不能实现材料自然情况下的最优分布。应根据受力特点及便于建模、制造来选择基结构。结合上述分析,如图6所示,机架侧板必不可少,不用分析;机架后挡板是一块钢板,用于安装照明等设施,也必不可少,不用进行优化;支撑卷筒等的壳体不用优化;机架下半部分的结构优劣直接决定了机架的承载能力,需优化。
最终,拓扑优化的初始模型为一中空的实体模型,其中壁厚参考原机架中矩形钢管的尺寸。考虑到原机架中卷筒、减速器的安装空间,初始模型采用中间挖空的做法。添加与原模型有限元分析相同的约束并施加载荷及边界条件。在分析中定义优化设计的响应为应变能及体积比。应变能作为目标函数使其最小,目的是提高结构刚度;体积比是约束条件,考虑到原机架使用中空型材或板件占用材料较少,因此约束体积比为0.15。提交分析,在分析中可看到整个过程共迭代10次达到收敛。

A.机架侧板 B.机架后挡板 C.支撑卷筒等的壳体 D.机架的下半部分
图7列出了优化后的单元密度结果。图7(b)的单元密度比起图7(a)有了显著变化;随着迭代过程的不断进行,单元密度由于惩罚函数的作用有了明显区分,图7(c)中单元密度为1的区域明显比图7(b)小,表明通过迭代优化了材料的分布;图7(d)表明应该把材料集中在机架的八条支撑腿上,对于安装电机处需要适当增加材料,另外矩形钢管截面形状采用长方形更好,因为其在垂直于一个方向有更好的刚度,机架底部没有材料,因此将原机架支腿底部的框架去除,机架上部保留的部分长宽比较大且向机架的横向、纵向延伸,在改进中用200×100的矩形钢管代替关键位置的100×100矩形钢管。
改进后的三维模型如图8所示。
4 优化后机架的受力变形分析及比较
为验证拓扑优化结果的可信性及合理性,采用有限元方法对其进行分析并比较优化前后的结果。将优化后的模型导入,为其设定与优化前分析相同的材料属性、分析步、耦合条件、载荷及边界条件、网格尺寸和网格类型进行分析。分析中共划分404040个单元。结果如图9。

图7 优化的迭代及其结果
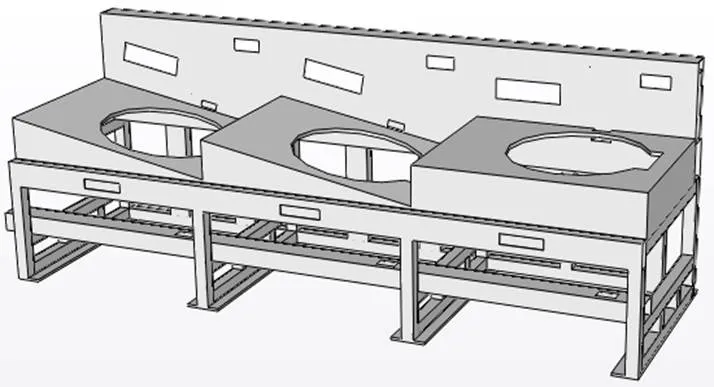
图8 优化后的机架
变形最大处仍为第三道次后方,因为其自重较大;前部变形较小,这是由于电机重量施加在机架后部。最大应力仍出现在第三道次机架后部支腿下方。应力及变形的分布与优化前基本一致,这和机架实际受力相符合。
在应力及变形的大小方面,对比拓扑优化前模型的分析结果,优化前后最大应力分别为34.45 MPa、21.33 MPa,下降了约38%;优化前后机架的最大变形量分别为0.0887 mm、0.0684 mm,下降了22.9%;此外由软件提供的数据,优化后机架的重量比原先减少59 kg,下降了9.2%。

图9 优化后机架的有限元分析结果
[1]李爱军. V型拉丝机的结构和特点[J]. 冶金设备,1992(3):58.
Optimization of the Drawing Machine Frame Based on the Finite Element Analysis
HUANG Zhongyong
( Sichuang Provincial Machinery Research & Design Institute, Chengdu 610063, China )
The drawing machine is used in drawing die wire drawing process of elastic deformation and plastic deformation principle, implementation of wire size and the physical properties change and mechanical equipment. Among them the strength of the frame will directly affect the production efficiency of drawing machine. At present the drawing machine manufacturing industry, the basic experience is used to design and manufacture, based on the analysis about the present situation of drawing machine frame, on the basis of combined the actual frame mechanical characteristics and the present situation of design, do the following three aspects. After the analysis of the stress of the drawing machine frame situation to simplify the geometry, and tetrahedron mesh. The topology optimization analysis drawing machine frame. According to the topology optimization analysis process of the rack, results, and to improve the original model, in order to ensure strength, optimize the structure.
drawing machine;frame;topology optimization analysis
TG355.1
A
10.3969/j.issn.1006-0316.2018.05.011
1006-0316 (2018) 05-0039-04
2017-12-20
黄仲勇(1979-),男,四川绵竹人,硕士,工程师,主要从事机械设计研发工作。
