高寒区引水渠道抽水融冰不冻长度计算模型及应用
2018-06-05宗全利郑铁刚吴素杰刘贞姬刘焕芳
宗全利,郑铁刚,吴素杰,刘贞姬,刘焕芳
(1. 石河子大学水利建筑工程学院,石河子 832000;2. 中国水利水电科学研究院流域水循环模拟及调控国家重点实验室,北京 100038)
0 引 言
中国北部冬季严寒,气温低且冰期长,导致大多数引水工程尤其是引水式电站的引水渠道产生不同程度的冰灾,这不仅影响渠道的输水能力,对农业生产和人民生活等都带来了一系列影响。为了防止这类灾情的发生,引水渠道中冰的产生及危害是必须考虑的关键因素[1-3]。而实际工程证明,抽水融冰技术的应用,对引水式电站渠道水温的提升有明显作用,可保证引水渠道冬季正常运行。
抽水融冰基本原理是采取凿井提取地下水注入引水渠,提高渠水的水温,使渠水中的冰花、冰块在温度较高水流的浸泡和冲刷下部分融化,控制渠道内底冰、岸冰发育,使渠道畅通,再利用地下水体流经电站形成的势能发电,使发电量大于或等于抽水的耗电量,从而产生增能作用,最后水体用于下游工、农业生产和人民生活。这种技术使地下水所具有的热能、势能、灌溉作用同时发挥,从而取得水利水电工程安全运行、发电、灌溉等水资源利用综合效益。
而抽水融冰应用的重要依据为不冻长度,即引水渠道水温大于 0 ℃的渠段长度。通过计算抽水融冰渠道的不冻长度便可知每一口融冰井对渠道冰害的防治距离,为寒区引水式电站运用抽水融冰技术提供参考依据。
目前国内外对河渠、水库水温变化及水中冰的形成演变等已有大量研究,且总结出了一些不冻长度计算的经验公式。其中前苏联和瑞典通过长期对渠道冰盖底部温度变化的研究,提出了至今仍然适用的预防及消除冰灾的措施[4];李克锋等考虑了气温、湿度、风速等因素,提出了可用于估算缺乏水温监测资料河流水温的新公式[5-6];王晓玲等[7-8]综合考虑了太阳辐射、水面的有效放射、水面蒸发热损及水面对流热损等因素的影响,模拟研究了不同气温条件下渠道水温的变化;白乙拉等[9]改进以前有关冰表面温度与气温关系表达式,并对改进了的一维热力学模型和单相Steften问题所采用的数值解法;吴剑疆等[10-12]均采用数值模拟的方法分析了河道、干渠沿程的水温变化,及水中冰的形成分布等规律;吴素杰等分别针对单井运行和多井同时运行条件下,对引水渠道水温变化过程进行了数值模拟,得到不同条件下各井不冻长度值以及井群合理优化布置方案[13-14];Shen等[15-17]综合考虑了风速、河冰水流的阻力等影响因素,提出了可以模拟过冷现象和底部冰的形成的RICEN模型,还模拟了Shokotsu河流冰塞的形成;Betchelor和Wadia研究了水中冰花密度及其热力交换[18-19];萨弗罗诺夫、邓朝彬、铁汉、王文学等分别结合实际工程提出了渠道不冻长度的经验公式,但各个不冻长度计算公式均有其一定的局限性,原苏联的萨弗罗诺夫公式和香加水电站公式仅考虑了混合水深、混合流速、混合水温,并未考虑外界气温等因素,无论外界大气温度有多低,其计算出的不冻长度是一样的,而新疆水利水电勘测设计院公式和金沟河公式较前两者加入考虑了外界气温的影响,但仍然忽略了地温、太阳辐射、风速等因素影响[4,20-22];王峰等以红山嘴电站为对象,计算了融冰井运行下渠道的不冻长度,并分析了各个融冰井的合理布置[23-25]。
根据以上研究表明,气温、地温、太阳辐射、风速等因素都会影响引水渠道的水温变化。但目前该方面的研究主要集中在河流中冰的形成和演化上,而关于不同水力、热力、气候条件下对渠道不冻长度的影响鲜有涉及。因此利用水流的热平衡理论推导出引水渠道的不冻长度统一计算公式,并分析不同水力、热力、气候条件对不冻长度的影响,为寒区引水式电站运用抽水融冰技术提供理论参考。
1 不冻长度的理论分析
根据水流的热平衡,抽水融冰引水渠道热量应满足方程:
W渠+W外=W′渠(1)
式中W渠为融冰井上游渠道热量,kJ/d;W′渠为融冰井下游渠道热量,kJ/d;W外为外界向渠道注入热量,kJ/d。
引起渠道水温变化的主要因素有:与大气之间的能量交换,即水面热交换;与河床的能量交换;降水等产生的能量交换;内部产生的热和人为的加热等。其中水面热交换包括太阳辐射(为太阳直接辐射和太阳散射辐射之和)、有效辐射、返回辐射热损失、蒸发热损失和对流热损失等。热量平衡关系可由单位水面面积在单位时间内的热耗失方程式表示,但要求方程式中全部要素的数值在实际中是不可能做到的,特别是对那些小河来说,所以忽略对热量平衡方程影响很小的要素,仅考虑主要要素,得到其平衡方程如下:

式中W注为从外界注入水(如泉水或井水)收入的热量,kJ/d;W辐为渠道水面所吸收的太阳直接辐射热和扩散辐射热,kJ/ d;W底为水与渠床之间的热量交换,kJ/d;W内为渠水内部动能转化为热能所吸收的热量,kJ/d;W返为水面返回辐射的热量损失,kJ/d;W蒸为渠水蒸发的热量耗失,kJ/d;W对为渠道水面与大气对流引起的热量交换,kJ/d;W雨雪为随降雨落入渠道中的热量或下雪时耗失的热量,kJ/d。
引水式电站抽水融冰引水渠道在冬季运行时,假设融冰井上游来流水温近似 0 ℃,当融冰井水注入后,渠道不结冰的渠段长度即为渠道的不冻长度L;理论上,当融冰井水注入长度等于不冻长度时,则融冰井运行效果最佳。不冻长度末端渠道水温近似 0 ℃,同时忽略渠道流量变化对渠道水温变化的影响(沿程渠道流量变化约1%~2%),由此可知:当渠水热量收入之和大于热量支出之和便可以保证渠道不会结冰,即正常运行。由式(2)可得:

即:

式中σ辐为每日每米渠道水面所吸收的太阳辐射热,kJ/(m·d);σ底为每日每米渠床与水之间的热量交换,kJ/(m·d);σ内为每日每米渠道渠水动能转化为热能所吸收的热量,kJ/(m·d);σ返为每日每米渠道水面返回辐射的热量损失,kJ/(m·d);σ蒸为每日每米渠道水面蒸发的热量耗失,kJ/(m·d);σ对为每日每米渠道水面与大气对流引起的热量交换,kJ/(m·d);σ雨雪为每日每米渠道随降雨落入渠道中的热量或下雪时耗失的热量,kJ/(m·d)。
平衡方程式(4)中各分量计算公式如下:
(1)渠水的总注入热储量

式中q注为外界注入水的流量,m3/s;c为热容量,文中c = 4.186 kJ/(kg·℃);t注为外界注入水的温度,℃;γ为水的密度,γ=1 000 kg/m3。
(2)为简化方程,本文参考文献[26],采用太阳总辐射估算每米渠道水面所吸收的太阳辐射热
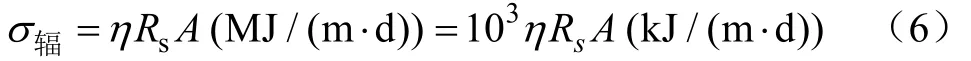
式中η为渠道水面吸收的太阳辐射系数,计算时取0.93;RS为太阳总辐射,MJ/(m2·d);A为每米渠道的水面面积,m2/m;根据《建筑设计资料集》查知每米渠道的水面面积A=10.6 m2/m。其中太阳总辐射RS可由下式方程估算:

式中n0为日照时数,h;N为可能的最大日照时数,h;as、bs为参数,其中as=0.25,bs=0.5;Ra为天文辐射,其计算方程如下[27]:

式中 Ra为天文辐射总量,MJ/(m2·d);T为周期,T=24×60×60s;I0为太阳常数,I0=13.67×10-4MJ/(m2·s);ρ为日地相对距离,m;ω0为日落时角,(°);φ为地理纬度,rad;δ为太阳赤纬,rad。
日地相对距离ρ可根据下式计算得出:

式中J为一年内的天数,J= 0~364;
日落时的太阳时角ω0可根据下式计算得出[23]:
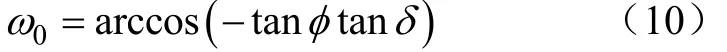
太阳赤纬δ可根据下式计算得出[28]:

根据玛纳斯县气象站资料,计算2013年3月的太阳总辐射量为 Rs=8.17 kcal/(cm2·月)=2 725 kcal/(m2·d)。
(3)每米渠床与水之间的热量交换

式中σ地底和σ地坡分别为每日每米渠底和渠坡与渠水的热量交换,kJ/(m·d);β地为渠道混凝土衬砌体的传热系数,为 24.7kcal/(m2·h·℃);A1和 A2分别为每米渠道渠底和渠坡的面积,A1=1 m2/m,A2=5.528 m2/m;t1和t2分别为渠底和渠坡地温的平均值,℃;t混为渠水与外界注入水的混合温度,℃。
(4)每米渠道渠水内部动能转化为热能所吸收的热量[4]
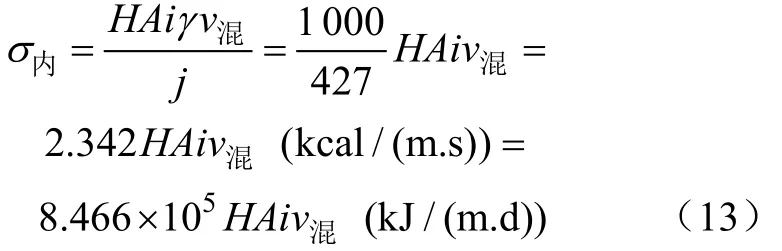
式中j为热功当量,j=427 kg·m/kcal;H为渠水的水深,本文为 2.743 m;A为每米渠道的水面面积,本文为10.6 m2/m;i为渠道的纵坡,本文为1/2 000;v混为渠道水混合后的流速,m/s。
(5)每米渠道水面返回辐射的热量损失[4]

式中n为天空被云所遮盖部分的分数,本文为0.6;t混为渠水与外界注入水混合后的温度,℃;t气为外界大气温度,℃。
(6)每米渠道水面蒸发的热量耗失

式中d为大气饱和差,即在一定的温度下饱和水汽压(E)与空气中实际水汽压(e)之差,Pa;v风为风速,m/s。根据玛纳斯县气象站资料,冬季常见风速v风=3 m/s,三月大气饱和差d=E-e=0.87 Pa。
(7)每米渠道水面与大气对流引起的热量交换

式中t混为渠水与外界注入水混合后的温度,℃;t气为外界大气温度,℃。
(8)每米渠道随降雨落入渠道中的热量或下雪时耗失的热量
空中降水落到渠面时,促使水流温度降低,因此降水对于冰的形成起着一定作用,而融化固态降水(降雪)所消耗的热量可能就很大。
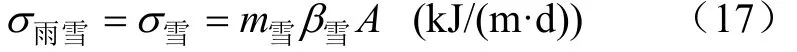
式中m雪为日降雪量,文中取 5.3 kg/(m2·d);β雪为雪的溶解热,为 80 kJ/kg;A为每米渠道的水面面积,为10.6 m2/m。
将式(5)~(17)代入式(4)得到不冻长度统一计算公式如下:

2 不冻长度公式验证及应用
2.1 原型观测
为验证不冻长度公式的可靠性与适用性,课题组于2013年3月21日,以新疆玛纳斯河流域的红山嘴电站二级引水渠道为研究对象(86o07′17″E,44o09′37″N),进行了水温、气温、引水渠道流量等因素原型观测试验,如图 1所示。水温和气温分别采用水银温度计和气温计测量,流量采用旋桨流速仪测量垂线平均流速计算得到;风速根据玛纳斯县气象站资料调查获得。二级引水渠道全长11 280 m,沿程共布设了13口融冰井,井水抽水量为0.13~0.24 m3/s,水温为9.6~10.6 ℃。原型观测当天气温均处于零下,可以保证观测条件,但观测过程中二级引水渠只有5#、6#、8#、9#、10#、11#和13#井正常工作,其余井未工作。
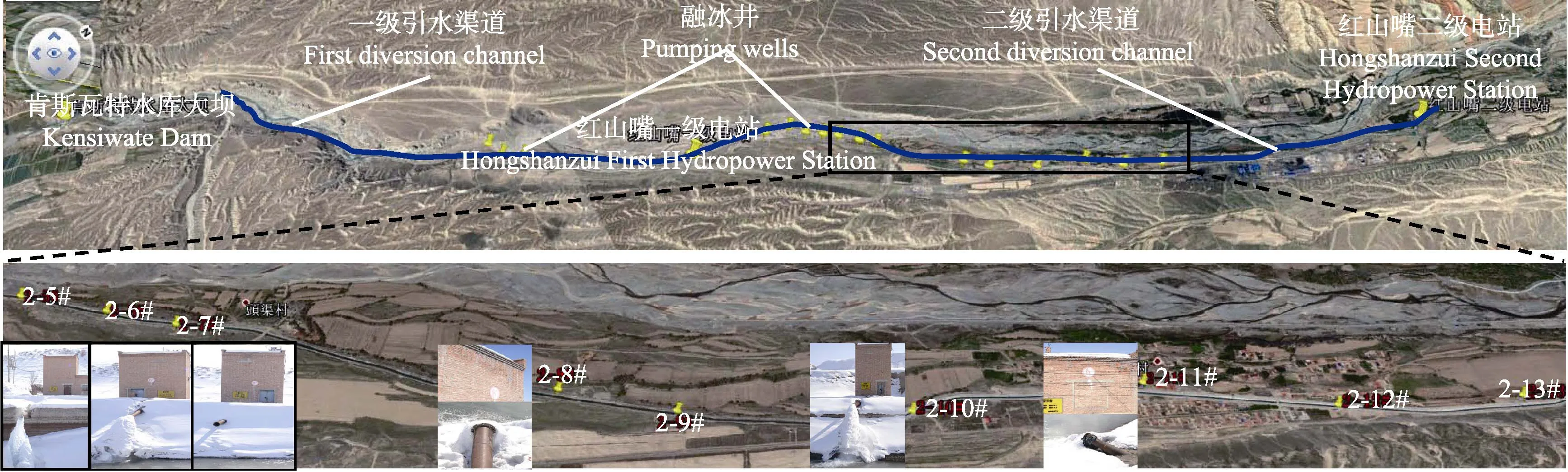
图1 抽水融冰原型观测现场Fig.1 Prototype observation site of pumping well water to melt ice
因受渠道地理位置影响不能直接进渠采集渠水温度,故选取塑料瓶 3次取水,并用水银温度计(量程为-50~20 ℃)多次测量取平均值;外界气温测量则在每个渠温采水点处放置 3支气温计取平均值,结果如表 1所示。测量过程中发现,融冰井水注入后,较高温度水迅速扩散,由于渠道内水温较低,因此渠水表面和内部温度会在很短时间内一致,所以实际中测量的表面渠水可以代表渠水温度。

表1 原型观测数据Table 1 Prototype measured data
2.2 公式验证
根据表1可知,除5#融冰井外,其他融冰井上游来流渠道水温均已明显高于 0 ℃,且沿程融冰井上游水温逐渐增加,表明在当时外界条件下不冻长度实际值大于融冰井间距。考虑到公式(18)设计之初假设上游来流接近0 ℃,结合红山嘴电站5#融冰井原型实测资料对不冻长度的各分量分别进行计算,可将不冻长度公式(18)简化如下:
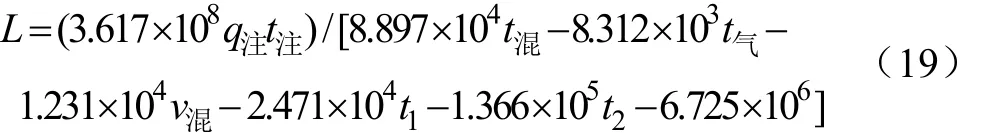
将红山嘴电站原型实测数据代入式(19),得到 5#融冰井运行下引水渠道的不冻长度计算结果如下表2。
根据表 2中计算出的不冻长度的结果得知,所计算的不冻长度值为17.6 km,大于红山嘴电站5#与6#融冰井之间间距400 m,这主要是由于原型观测时外界气温较高(-3.0 ℃)。根据王峰等对红山嘴电站冬季抽水融冰运行下不冻长度的原型运行资料[23,29],以及王文学等对金沟河电站冬季渠道升温运行下不冻长度的原型资料[22],利用式(18)进行计算,得到不冻长度计算结果如表 3所示。在红山嘴电站大气温度为-32.0~-18.2 ℃下,原型观测不冻长度为1 875~2 000 m,计算得到不冻长度为1 580~2 594 m,误差率为15.9%~29.5%;金沟河电站在大气温度为-24.1~-16.3℃下,原型观测不冻长度为4 099~6 415 m,计算得到不冻长度为4 618~6 823 m,两者计算结果与原型观测结果基本一致,误差率为6.2%~14.1%。
根据不冻长度计算结果可知,利用推导公式计算的红山嘴电站和金沟河电站不冻长度计算结果与实测结果相近,说明本文公式的可靠性。由于该式综合考虑了渠道混合流量、渠道混合水温、渠道混合流速、大气温度、风速、大气饱和差、降雪量、太阳辐射量、地温等多因素的影响,不仅符合热平衡原理,使计算结果更为准确,而且完全可以适用于各电站的不冻长度计算,适用范围更为广泛。

表2 红山嘴电站引水渠道不冻长度计算结果Table 2 Calculated results of ice-free water length of diversion channel for Hongshanzui hydropower station

表3 各电站引水渠道不冻长度计算结果Table 3 Calculated results of ice-free water length of diversion channel for each hydropower station
2.3 与其他公式的对比
下面以红山嘴电站为对象,根据其原型实测资料,应用各不冻长度公式分别计算出不冻长度,结果如图 2所示,并分析比较每个公式的优缺点。

图2 不同气温条件下各不冻长度计算结果对比Fig.2 Comparison of calculated results of ice-free water length under different temperatures
从图2可以看出,原苏联萨费罗诺夫公式L苏、香加水电站公式1L香、2L香计算出的不冻长度结果呈线性趋势变化,而新疆水利水电勘测设计院公式L勘、金沟河公式L金以及本文推导公式的不冻长度计算结果呈乘幂趋势变化。从图 2中还可以看出,各计算公式得到的不冻长度结果差别较大,原苏联萨费罗诺夫公式L苏和香加水电站公式1L香、2L香计算结果显示随着气温下降不冻长度变化趋于平缓,且无论外界大气温度有多低,其不冻长度几乎相等,这显然与不冻长度随温度降低而变短的规律不一致[30],所以这 3个公式都有各自的适用条件;究其原因,主要为各公式均是以某一电站引水渠道为原型所得到的经验公式,考虑影响因素较少,使得计算结果发生较大变化。例如:原苏联萨费罗诺夫公式假设渠道深度1 m,渠水流速1.0 m/s,渠水水温0.2 ℃,其不冻长度计算结果为670 m;计算表明,即使热耗失不大,亦即在温度较高气候条件下,计算得到不结冰的引水渠道的容许长度也是很小的,因此,该公式仅适用于当水源是温暖的泉水补给,或者当上游具有较大蓄水库且引水渠道明流部分较短的情况。
根据本文公式L推和金沟河公式L金计算结果,随着气温下降,不冻长度缩短较快,其变化较为明显;但从图中明显可以看出,金沟河公式计算结果数值偏差较大,不冻长度最长达到8 km,并不符合实际,因此该式仅适用于引水渠道流量较小(Q < 4m3/s),与实测值误差率为6.2~14.1%。对于红山嘴电站(Q=10.16~11.18 m3/s)这类渠道引水流量较大的电站并不适用。
根据新疆水利水电勘测设计院公式计算结果还可以看出,随着气温的降低,在一定范围内,不冻长度基本保持不变,这主要是由于该公式综合系数 K值在一定气温范围内是定值,所以该公式只能适用于一定气温范围内的不冻长度计算,仅适用于渠水流速0.8~1.2 m/s,冬季风速≤5 m/s,渠底高于地下水位的挖方混凝土板衬砌渠道[24];而红山嘴电站冬季运行引水渠道流速范围为0.6~0.7 m/s,所以该公式也不能用于计算红山嘴电站引水渠道不冻长度。
综上分析可知,各个冻长度均有其一定的适用性,但目前已有的 5个不冻长度公式对于红山嘴电站引水渠道均不适用。而本文根据水流的热平衡理论推导出不冻长度计算公式,综合考虑了各因素的影响,适用范围更为广泛,下面将结合计算结果进一步分析在不同水力、热力、气候条件下不冻长度的变化规律。
2.4 不冻长度的影响因素分析
从推导出的不冻长度公式(18)可以发现不冻长度与渠道混合流量水温、太阳辐射量成正比,与大气温度、风速、大气饱和差、日降雪量成反比,为进一步了解各因素对不冻长度的影响,下面以红山嘴电站 5#融冰井为例,对不冻长度的主要影响因素进行分析。
2.4.1 渠道流量对不冻长度影响
由式(18)可知,渠道来水流量的变化主要对渠水内部动能转化为热能所释放的热量σ内产生影响,假设外界大气温度为-20 ℃时,融冰井注入流量为0.16 m3/s,其他条件不变(井水注入量q注=0.16 m3/s;渠水混合温度t混=0.335 ℃;风速v风=3.0 m/s;渠道混凝土衬砌体传热系数β地=24.7 kcal/(m2·h·℃);日降雪量 m雪=5.3 kg/(m2·d);雪溶解热β雪=80 kJ/kg;每米渠水面积A=10.6 m2/m;渠水吸收太阳辐射系数 η=0.93;太阳总辐射量Rs=2725 kcal/(m2·d);太阳散射辐射热占总辐射热百分比a=0.06,不冻长度随渠道流量变化如图3所示。受限于渠道断面,因此本文渠道流量研究范围设为0~20 m3/s,由图示结果可知,随着渠道来水流量的增加,σ内逐渐增大,但不冻长度变化较小,仅由3.2 km变化到3.4 km,由此表明该范围内渠道流量仅为影响不冻长度的次要因素,文献[3-4]中河道水温预测通常忽略流量而主要考虑外界气象条件因素也充分说明了这一点。
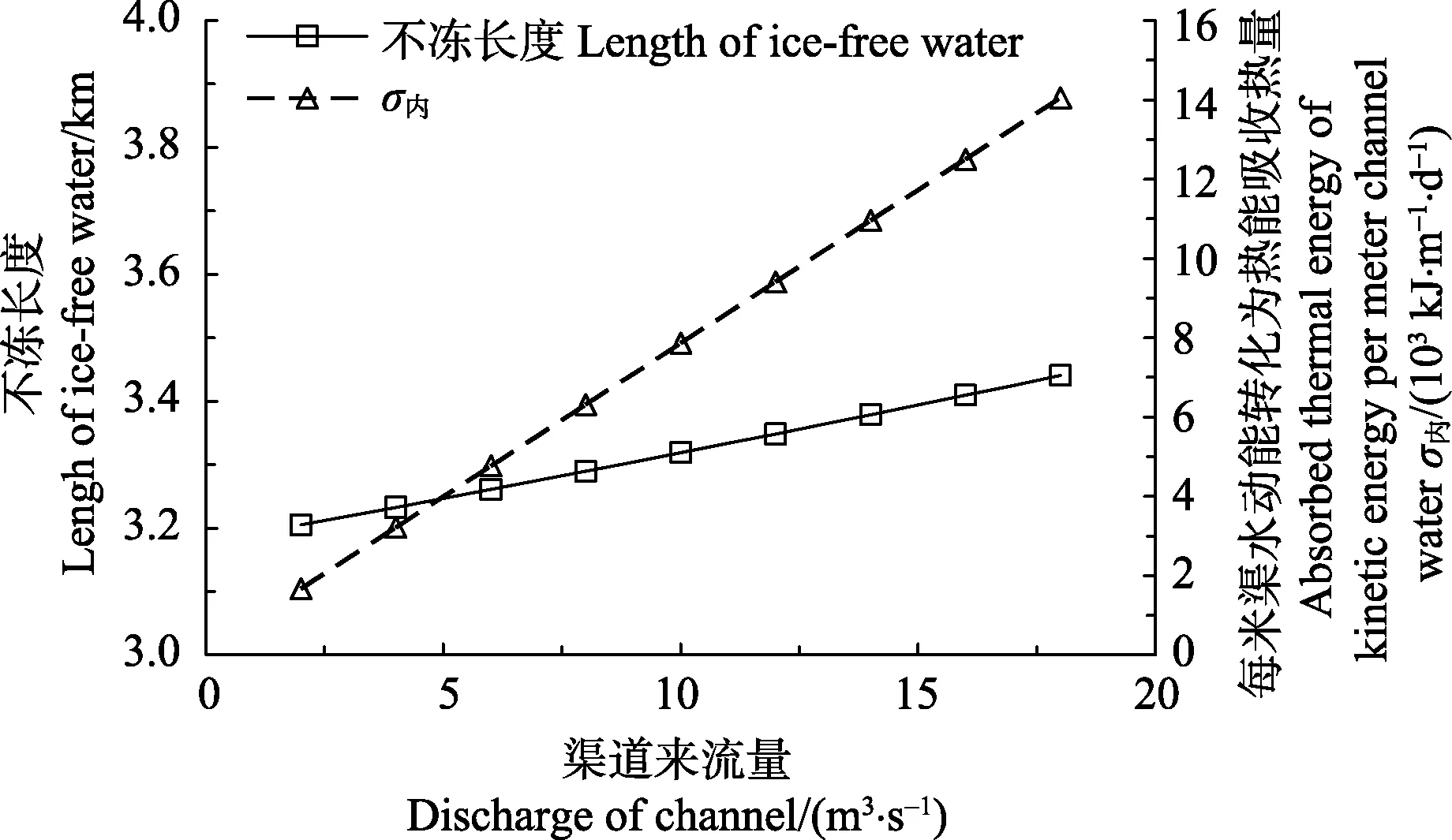
图3 渠道来水流量对不冻长度的影响Fig.3 Effect of channel discharges on length of ice-free water
2.4.2 井水注入量对不冻长度影响
井水注入热通量对不冻长度将产生直接影响,而井水热通量与注入流量和注入水温相关。根据抽水融冰原理可知,注入水温由水源决定,实际工程中难以发生改变,故本节假设外界大气温度为-20 ℃时,其他条件不变(渠水混合温度t混=0.335 ℃;风速v风=3.0 m/s;渠道混凝土衬砌体传热系数β地=24.7 kcal/(m2·h·℃);日降雪量m雪=5.3 kg/(m2·d);雪溶解热β雪=80 KJ/kg;每米渠水面积A=10.6 m2/m;渠水吸收太阳辐射系数η=0.93;太阳总辐射量Rs=2725 kcal/m2·d;太阳散射辐射热占总辐射热百分比a=0.06,仅改变井水注入量(q注=0.04、0.06、0.08、0.10、0.12、0.14、0.16、0.18、0.20 m3/s等),研究其对渠道不冻长度的影响规律,结果如图4所示。

图4 井水注入量对不冻长度的影响Fig.4 Effect of well discharges on length of ice-free water
从图4可以看出,由井水注入的热量W注与不冻长度成正比关系,随着井水注入热量的增加,渠道的不冻长度不断增加,且井水注入量每增加 0.02 m3/s,渠道的不冻长度便以每400 m左右递增,由此表明,井水注入热量W注对渠道的不冻长度有着显著影响,即在实际工程中,增加井水注入量是提高渠道混合水温、增大渠道不冻长度,防止渠道冬季运行冰害最直接有效的方法。
2.4.3 大气温度对不冻长度影响
根据式(5)~(17)可知,大气温度仅对每米渠道水面的有效放射σ返和大气对流交换引起的热量损失σ对有影响。本节仅改变外界大气温度,其余因素不变,对渠道不冻长度和大气对流交换引起的热量损失σ对进行计算,结果如图5所示。

图5 大气温度对不冻长度的影响Fig.5 Effect of atmospheric temperature on length of ice-free water
由图 5可知,当其他因素保持不变时,外界大气温度与每米渠道水面与大气对流交换引起的热量损失σ对成反比,且大气温度每降低 1 ℃,每米渠道水面与大气对流交换引起的热量损失将增大8.3×103KJ/m·d,说明气温对每米渠道水面与大气对流交换引起的热量损失的影响较大。还可以发现,外界大气温度与渠道不冻长度呈乘幂趋势变化,且随着大气温度的降低,不冻长度越短,且气温每降低5 ℃,不冻长度减小的最大幅度为31.3%,最小幅度为16.1%,说明大气温度对不冻长度影响较为显著。在实际工程中,外界气温无法人为控制,随着气温降低,渠道不冻长度变短。
2.4.4 风速对不冻长度影响
从式(15)、(16)中可知,每米渠道水面蒸发的热量耗失和每米渠道水面与大气对流交换引起的热量损失均与风速有关,风速变大,无疑会加大水面蒸发和水面与大气对流交换。当大气温度为-20 ℃,渠道混合流量、温度、太阳辐射量、日降雪量等其他条件不变时,对不同风速下(v风=0.5~6.0 m/s)的不冻长度进行计算,结果如图6所示。

图6 风速对不冻长度的影响Fig.6 Effect of wind speed on length of ice-free water
从图 6可以发现,风速与每米渠道水面蒸发的热量耗失、每米渠道水面与大气对流交换热损均呈对数趋势变化,且风速每增加1 m/s,每米渠道水面蒸发的热量耗失和每米渠道水面与大气对流交换的热损均成倍增加,这无疑会影响渠道的不冻长度。还可知不同风速条件下,渠道不冻长度呈乘幂趋势变化,且随着风速加大,渠道不冻长度也越短,且不冻长度减小的最大幅度为53.0%,最小幅度为4.30%,说明风速对不冻长度的影响也较为明显。因而在实际工程中,引水式电站引水渠道应修建在风速较缓或者挡风处,以减小渠道水面与大气交换的热量损失和水面蒸发热损。
3 结 论
根据水流的热平衡方程推导出渠道的不冻长度计算公式,并以红山嘴电站原型实测数据进行了验证;分析了不同水力、热力、气候条件对渠道不冻长度的影响,主要结论如下:
1)利用原型实测资料对得出的不冻长度进行了计算,结果显示:在红山嘴电站大气温度为-32.0~-18.2℃下,计算不冻长度为1 580~2 594 m,误差率为15.9%~29.5%;金沟河电站大气温度为-24.1~-16.3℃下,计算不冻长度为4 681~6 823 m,误差率为6.2%~14.1%,两者计算结果与原型观测结果基本一致,证明不冻长度公式的可靠性。
2)根据不冻长度计算公式可知,不冻长度与渠道来水流量、井水注入量、井水水温、太阳辐射量成正比,与大气温度、风速、大气饱和差、日降雪量成反比。
3)当渠道来水流量为0~20 m3/s时,单因素改变渠道来水流量,不冻长度变化较小,仅增加200 m,由此表明该范围内渠道来水流量的变化对不冻长度影响较小。
4)当外界大气温度为-20℃时,仅改变井水注入量(q注=0.04、0.06、0.08、0.10、0.12、0.14、0.16、0.18、0.20 m3/s),保持其他条件不变,计算不冻长度,结果表明:井水注入量越大,渠水收入的热量W水越大,渠道的不冻长度也越大,井水注入量每增加 0.02 m3/s,渠道的不冻长度便以每400 m左右递增,说明渠道井水注入量对不冻长度的影响较为显著;在实际工程中,增加井水的注入量是提高渠道水温,增大渠道不冻长度,防止渠道冬季运行冰害最直接有效的方法。
5)在相同环境下,仅改变外界大气温度(当t气=-10、-11、-12、-13、-14、-15℃),对渠道不冻长度进行计算,结果表明:外界大气温度与每米渠道水面的有效放射的热量损失、每米渠道水面与大气对流交换引起的热量损失成反比,与渠道的不冻长度成正比,且气温每降低5 ℃,不冻长度减小的幅度为16.1%~31.3%,说明大气温度对不冻长度影响较为显著。
6)在大气温度为-20℃时,保持其他条件不变时,对不同风速(v风=0.5~6.0 m/s)下的不冻长度进行计算,结果表明:风速与渠道的不冻长度成反比,随着风速的加大,渠道的不冻长度变短,且不冻长度减小的幅度为4.30%~53.0%,说明风速对不冻长度的影响也较明显。
[1] 陈明千. 西藏高寒地区引水渠道冰花生消规律研究[D].成都:四川大学,2006.Chen Mingqian. Study on the Process of Ice Formation and Melting in Diversion Channel of Tibet[D]. Chengdu:Sichuan University, 2006. (in Chinese with English abstract)
[2] Shen Hungtao. Mathematical modeling of river ice processes.Cold Regions Science and Technology[J]. 2010, 62 (1): 3-13.[3] Richard L Stockstill, Steven F Daly, Mark A Hopkins.Modeling floating objects at river structures, Journal of Hydraulic Engineering, ASCE[J]. 2009, 135 (5): 403-414.
[4] 波达波夫,Поталов著. 杜一民译. 引水道式农村水电站的冰冻问题[M]. 北京:水利电力出版社,1959.
[5] 李克峰,郝红升,庄春义,等. 利用气象因子估算天然河道水温的新公式[J]. 四川大学学报:工程科学版,2006,38(1):1-4.Li Kefeng, Hao Hongsheng, Zhuang Chunyi, et al. A new method for predicting water temperature of river by using meteorological factors[J]. Journal of Sichuan University:Engineering Science Edition, 2006, 38(1): 1-4. (in Chinese with English abstract)
[6] 辛向文,周孝德. 天然水温估值计算方法研究[J]. 水资源与水工程学报,2010,21(2):124-127.Xin Xiangwen, Zhou Xiaode. Study on the method for predicting water temperature of river[J]. Journal of Water Resources &Water Engineering, 2010, 21(2): 124-127. (in Chinese with English abstract)
[7] 王晓玲,张自强,李涛,等. 引水流量对引水渠道中水内冰演变影响的数值模拟[J]. 水利学报,2009,40(11):1307-1312.Wang Xiaoling, Zhang Ziqiang, Li Tao, et al. Numerical simulation of diversion water flux effect on frazil ice evolution in diversion channel[J]. Journal of Hydraulic Engineering, 2009, 40(11): 1307-1312. (in Chinese with English abstract)
[8] 王晓玲,周正印,蒋志勇,等. 考虑气温变化影响的引水渠道水内冰演变数值模拟[J]. 天津大学学报:自然科学与工程技术版,2010,43(6):515-522.Wang Xiaoling, Zhou Zhengyin, Jiang Zhiyong, et al.Numerical simulation of frazil ice evolution in diversion channel considering effect of temperature variation[J].Journal of Tianjin University: Science and Technology, 2010,43(6): 515-522. (in Chinese with English abstract)
[9] 白乙拉,李冰,冯景山. 以气温为边界条件的水库冰盖厚度的数值模拟研究[J]. 辽宁师范大学学报:自然科学版,2012,35(2):164-167.Bai Yila, Li Bing, Feng Jingshan. Study on numerical simulation of growth in thickness of ice caps in reservoirs in the boundary condition of atmospheric temperature[J].Journal of Liaoning Normal University: Natural Science Edition, 2012, 35(2): 164-167. (in Chinese with English abstract)
[10] 吴剑疆,茅泽育,王爱民,等. 河道中水内冰演变的数值计算[J]. 清华大学学报:自然科学版,2003,43(5):702-705.Wu Jianjiang, Mao Zeyu, Wang Aimin, et al. Numerical simulation of frazil ice evolution in rivers[J]. Journal of Tsinghua University: Natural Science, 2003, 43(5): 702-705.(in Chinese with English abstract)
[11] 茅泽育,吴剑疆,张磊,等. 天然河道冰塞演变发展的数值模拟[J]. 水科学进展,2003,14(6),700-705.Mao Zeyu, Wu Jianjiang, Zhang Lei, et al. Numerical simulation of river ice jam[J]. Advances in Water Science,2003, 14(6), 700-705. (in Chinese with English abstract)
[12] 茅泽育,许昕,王爱民,等. 基于适体坐标变换的二维河冰模型[J]. 水科学进展,2008,19(2),214-223.Mao Zeyu, Xu Xin, Wang Aimin, et al. 2D numerical model for river-ice processes based upon body-fitted coordinate[J].Advances in Water Science, 2008, 19(2), 214-223. (in Chinese with English abstract)
[13] 吴素杰,宗全利,郑铁刚,等. 高寒区引水渠道抽水融冰水温变化过程模拟[J]. 农业工程学报,2016,32(14):89-96.Wu Sujie, Zong Quanli, Zheng Tiegang, et al. Simulation on water temperature change process of diversion channel for pumping well water to melt ice at high altitude and cold regions[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016,32(14): 89-96. (in Chinese with English abstract)
[14] 吴素杰,宗全利,郑铁刚,等. 高寒区多口融冰井引水渠道水温变化三维模拟及井群优化布置[J]. 农业工程学报,2017,33(14):130-137.Wu Sujie, Zong Quanli, Zheng Tiegang, et al. 3D simulation on water temperature change of diversion channel and optimal arrangement of multi-wells at high altitude and cold regions[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017,33(14): 130-137. (in Chinese with English abstract)
[15] Shen Hungtao, Liu Lianwu. Shokotsu river ice jam formation[J]. Cold Regions Science and Technology, 2003,37(1): 35-49.
[16] Shen Hungtao, Su Junshan, Liu Lianwu. SPH simulation of river ice dynamics[J]. Journal of Computational Physics,2000, 165(2): 752-770.
[17] Shen Hungtao. Research on river ice processes: Progress and missing links[J]. Journal of Cold Regions Engineering, 2003,17 (4): 135-142.
[18] Betchelor G K. Mass transfer from small particles suspended in turbulent fluid[J]. Journal of Fluid Mechanics, 1980, 98:609-623.
[19] Wadia P H. Mass Transfer from Sphere and Discs in Turbulent Agitated Vessels[D]. Massachusetts: Department of Chemical Engineering, Massachusetts Institute of Technoligy,1974.
[20] 邓朝彬,刘柏年. 香加水电站引水渠冬季注水升温运行发电实践经验介绍[J]. 农田水利与小水电,1987,07:43-45.
[21] 铁汉. 寒冷地区水电站引水明渠冬季不结冰长度计算[J].西北水电,1999,(1):23-24,26.
[22] 王文学,丁楚建. 抽井水入发电渠道冬季运行试验及其计算[J]. 农田水利与小水电,1991(12):35-41, 48.Wang Wenxue, Ding Chujian. Experiments and calculations for winter operation with pumping well water into power canal[J]. China Rural Water and Hydropower, 1991, (12):35-41, 48. (in Chinese with English abstract)
[23] 王峰,吴艳华,马月俊,等. 红山嘴梯级水电站抽水融冰技术应用与探讨[J]. 河南水利与南水北调,2009,07:111-112.
[24] 刘新鹏,张治山,陈荣. 梯级引水式水电站群提高发电生产能力的途径[J]. 中国水能及电气化,2007(9):38-43.Liu Xinpeng, Zhang Zhishan, Chen Rong. Ways of improving the generation output by cascade-diversion type power station[J]. China Water Power and Electrification,2007(9): 38-43. (in Chinese with English abstract)
[25] 刘新鹏,陈荣,张治山. 红山嘴电厂抽水融冰技术新探索[J]. 中国水能及电气化,2008(4):29-36.
[26] Allen R G, Pereira L S, Raes D, et al. Crop evapotranspiration:Guidelines for computing crop requirements[Z]. Irrigation and Drainage Paper No.56, 1998, FAO, Rome, Italy.
[27] 高国栋,缪启龙,王安宇,等. 气候学教程[M]. 北京:气象出版社,1996:31-32.
[28] 刘钰,Preira L S,Teixira J L,等. 参照腾发量的新定义及计算方法对比[J]. 水利学报,1997(6):27-33.Liu Yu, Preira L S, Teixira J L, et al. Update definition and computation of reference evapotranspiration comparison with former method[J]. Journal of Hydraulic Engineering, 1997,(6): 27-33. (in Chinese with English abstract)
[29] 铁汉,朱瑞森. 论水电站防冰工程技术[J]. 东北水利水电,1993,(1):3-8.
[30] 赵梦蕾,刘贞姬,宗全利. 引水渠道单井注水对不冻长度的影响[J]. 中国农村水利水电,2016,4:144-149.Zhao Menglei, Liu Zhenji, Zong Quanli. The influence of the length of the ice-free water with single well[J]. China Rural Water and Hydropower, 2016, 4: 144-149. (in Chinese with English abstract)
