计及间隔的组合磁极无刷直流电机优化设计

何智荣，杨向宇，赵世伟



计及间隔的组合磁极无刷直流电机优化设计

何智荣，杨向宇，赵世伟

（华南理工大学电力学院，广州 510641）

本文提出一种永磁磁极间隔和组合磁极相结合的新型永磁无刷直流电机转子磁极结构，利用多块不等磁能积的永磁体替代每极的单块永磁体，在降低稀土永磁材料用量的同时，改善相绕组反电动势波形。本文针对四极无刷直流电机，依据主副磁极的位置形状和剩磁强度比例，以空载反电动势正弦化程度为优化目标，采用田口法对选定的优化参数进行正交试验。评估各个参数对优化目标的权重比例，从而选定优化设计方案，通过有限元仿真结果验证了该优化方法可有效提高电机性能。

无刷直流电机；组合磁极；分块磁极；反电动势

0 前言

目前，永磁无刷直流电动机具有高效、高功率密度、高可靠性及控制方便和成本更低等显著特点，在伺服控制、电动汽车、机器人技术、医疗设备及家用电器等领域得到了越来越广泛的推广应用[1]。以方波驱动时，无刷直流的电磁转矩较大，但其劣势在于：1）转矩脉动大；2）高速工作时，矩形电流波形发生较大程度的畸变，引起转矩的下降；3）定子磁场非连续旋转磁场，定子铁心附加损耗增加。采用正弦波驱动时，相同尺寸的永磁同步电机转矩脉动较低。空载反电动势正弦化的无刷直流电机采用正弦波驱动，则可望降低转矩脉动和噪声，能够兼顾性能和成本的要求[2-4]。

目前，对无刷直流电机的反电动势正弦化研究主要基于气隙磁密正弦化设计。文献[5]中，利用转子气隙不均匀来降低反电动势畸变率；文献[6]、[7]中研究了通过组合磁极降低反电动势畸变率；文献[8]研究了通过Halbach磁极结构进行特别设计使气隙磁密波形正弦化，减小反电动势谐波含量；文献[9]研究了极数与槽数组合对于反电动势正弦化程度的影响；文献[10]研究了永磁磁极间隔对空载反电动势正弦化程度的影响，提出了确定永磁体排列的优化方法。

本文针对集中式绕组的表贴式无刷直流电机特性，研究了计及间隔的组合磁极转子磁极来削弱反电动势波形畸变率THD。通过合理选择多块不等磁能积永磁体的位置形状组合，可有效减小反电动势的谐波、削弱转矩脉动。采用田口法评价各参数对反电动势谐波含量的影响，并与组合磁极和磁极间隔优化设计进行对比。

1 模型的优化设计

1.1 电机的基本参数

本文以六槽四极集中式绕组的表贴式无刷直流电机为例，结构模型如图1所示。每极由若干块不同永磁材料的磁钢构成，中间两块为磁能积较高的稀土永磁体，两侧为对称的磁能积较小的铁氧体永磁体，充磁方向长度相同、宽度不同。无刷直流电机的基本参数见表1。

每极永磁体分块过多，易导致制作工艺复杂、成本上升。选用磁极间隔优化反电动势，当分块较少时，反电动势正弦化程度不高；选择组合磁极优化反电动势波形时，由于磁极分块较少，气隙磁密正弦化程度不高使反电动势波形畸变率较大。图1所示即为4块永磁体作为转子一极的结构示意图。

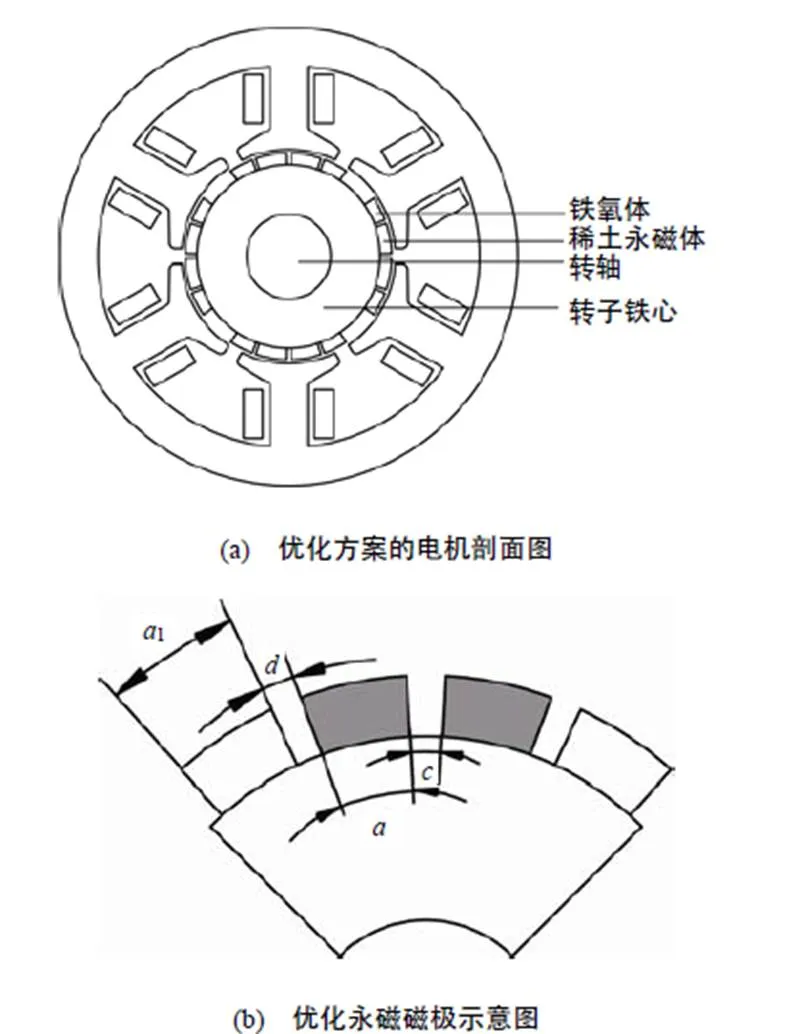
图1 六槽四极无刷直流电机拓扑图

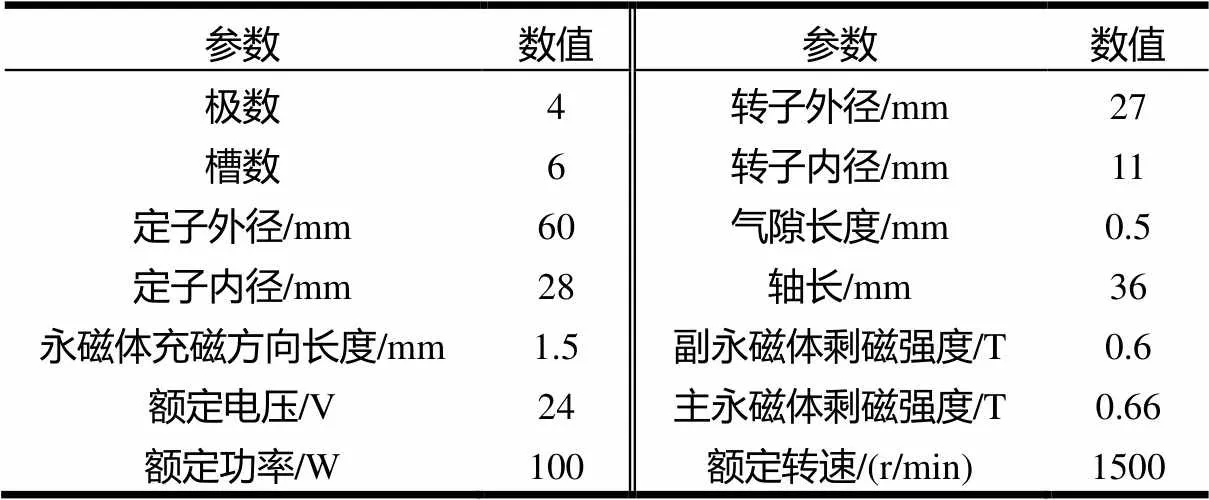
表1 样机主要参数取值表

1.2 数学模型

根据法拉第电磁感应定律可知，相绕组反电动势为：

式中，为相绕组交链的磁通。根据式（1）中，推导出若有正弦磁链波形，可得正弦反电动势波形。

若忽略饱和、漏磁、定子开槽的影响，并假设永磁体的磁导率与空气相同，气隙磁密公式如下：

式中，r()表示永磁体的剩磁强度，m表示永磁体的充磁方向长度，()表示有效气隙长度。

根据本文优化设计，通过对永磁材料、形状位置的选择，求解式（2），可得气隙径向磁密沿电枢表面分布，如图2所示。

图2 计算气隙磁密波形

实线为此优化转子的径向气隙磁密波形，虚线为单一永磁磁极转子的径向气隙磁密波形。

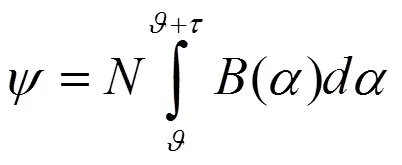
综合式（2）和式（3），求得相绕组磁链波形如图3所示。

图3中实线为优化设计的相绕组磁链，虚线为单一永磁磁极的相绕组磁链。优化设计方案有效提高磁链正弦化程度，降低反电动势波形畸变率。

2 基于田口法的电机优化设计

2.1 田口正交实验设计

为衡量空载反电动势波形正弦化程度，将其进行傅里叶分析，以反电动势波形畸变率表征整体正弦化程度。考虑到电机驱动中高频开关带来高次反电动势谐波不可避免，本文的主要研究对象是3~11次反电动势谐波，作为反电动势波形畸变率的研究对象。

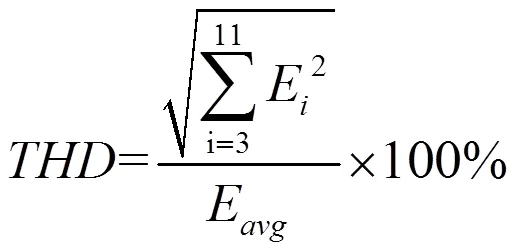
式中，E为电机反电动势次谐波幅值，Evg为平均反电动势幅值。

在减小反电动势波形畸变率的同时，不能对反电动势基波幅值造成过大的损失，故而选择反电动势基波幅值ml作为第二优化目标。

为优化空载反电动势波形，根据前期仿真结果及部分优化参数经验，每个优化参数选取4个水平，电机具体优化参数和水平值见表2。

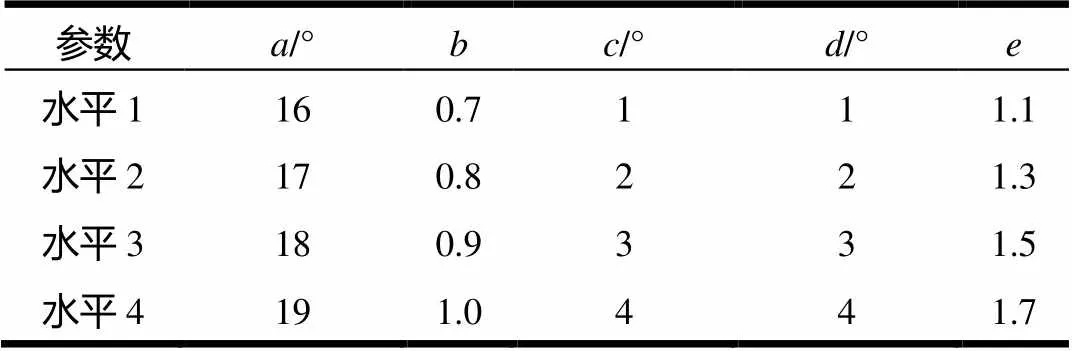
表2 样机主要参数取值表

表2中共有45=1024种组合情况，通过上述正交实验设计，只需要通过16次实验分析，可以代表1024次实验的组合结果。所建正交表及有限元分析结果见表3。

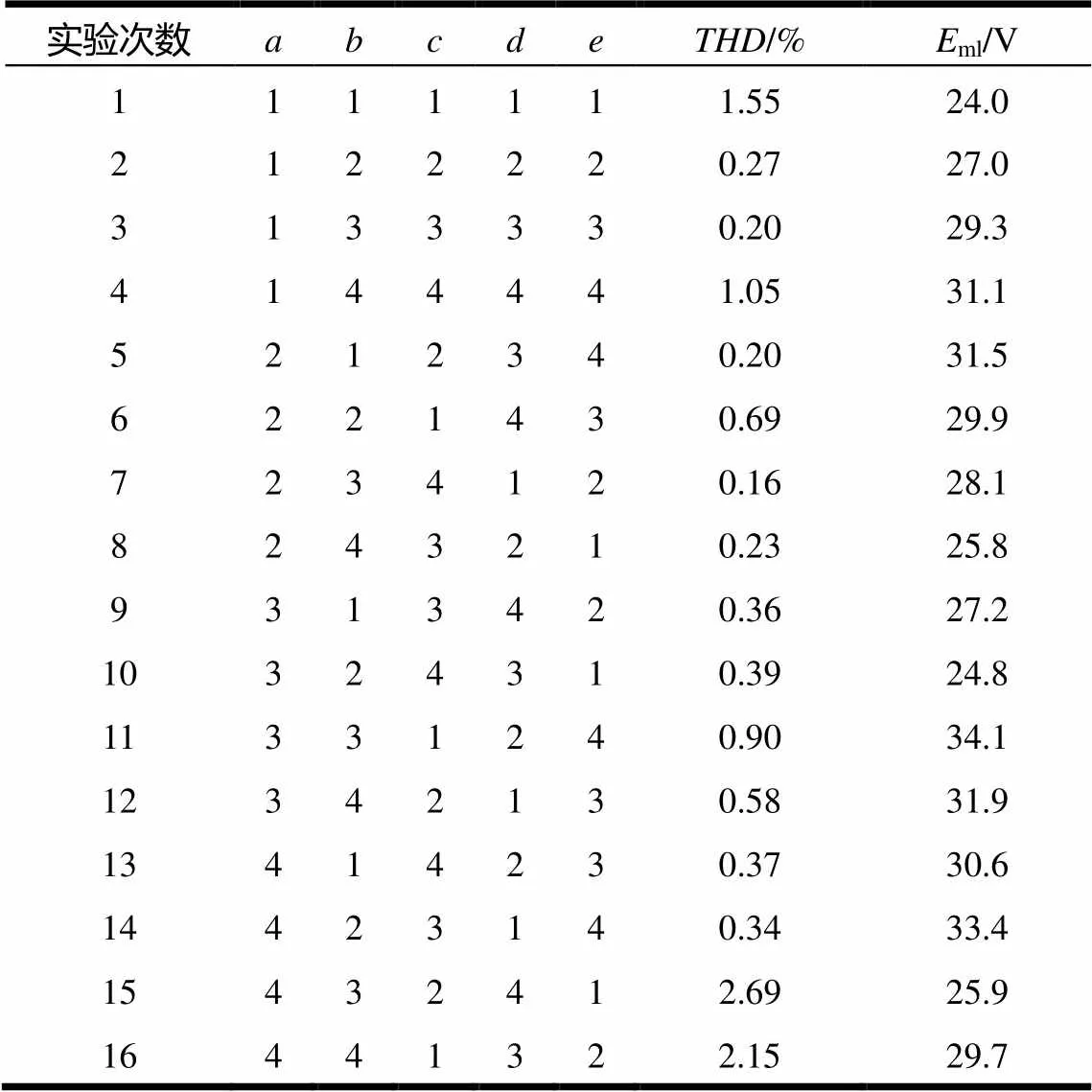
表3 实验矩阵及有限元分析结果

2.2 参数变化对各性能指标所占的比重

为分析每个参数对电机性能指标的影响，需求解每个参数的改动对应某一性能指标下计算结果的平均值，例如主永磁磁极宽度取水平1时的反电动势波形畸变率[11]，计算方法如下：

其中，（）是表3中第次正交实验所对应的反电动势畸变率。

求解各个影响因子指标的平均值见表4。

表4 影响因子对应反电动势谐波的平均值

表5 影响因子对应反电动基波势幅值的平均值

下一步应用方法分析法（ANOVA）计算各个影响因子与平均值差的平方和（SSA），凭此来判断各影响因子对最终结果影响的大小。求解公式如式（6）所示[12-13]。

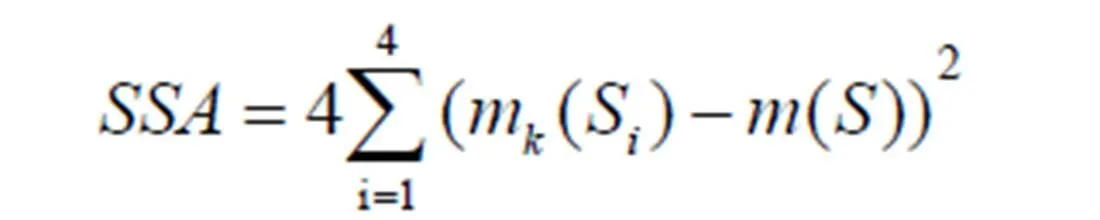
式中，代表主永磁体宽度等参数；为电机各影响因子；k(i)为表4中参数下的第个水平下的平均值；()为的平均值。各影响因子对目标函数的影响所占的比重统计见表6。

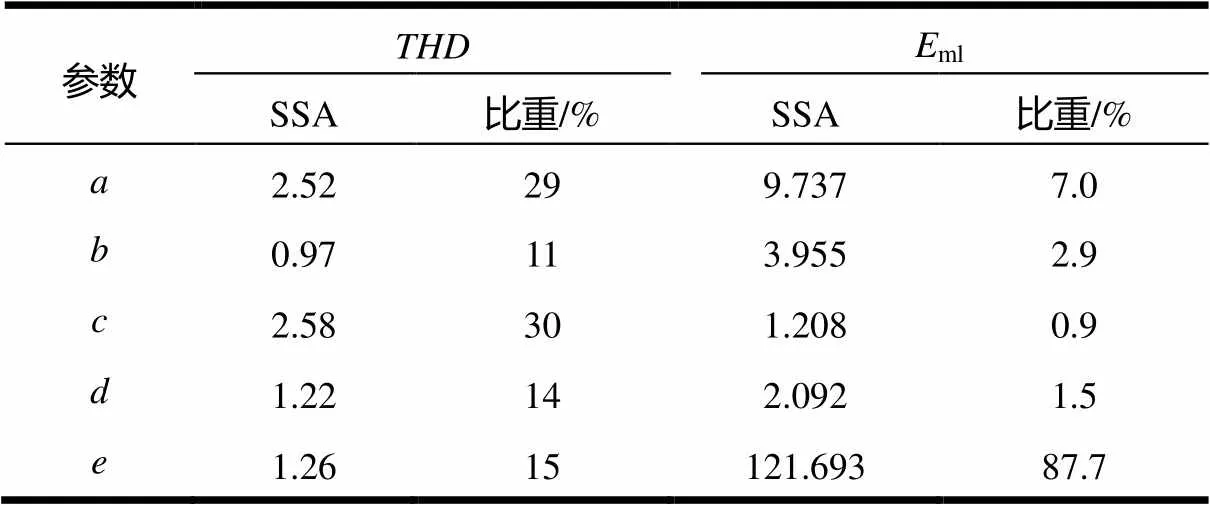
表6 各影响因子对目标函数的影响所占比重

3 结果分析

将各参数的取值对目标函数的影响应用图像分析更为直观，图4显示出不同参数变化对和ml的影响趋势。

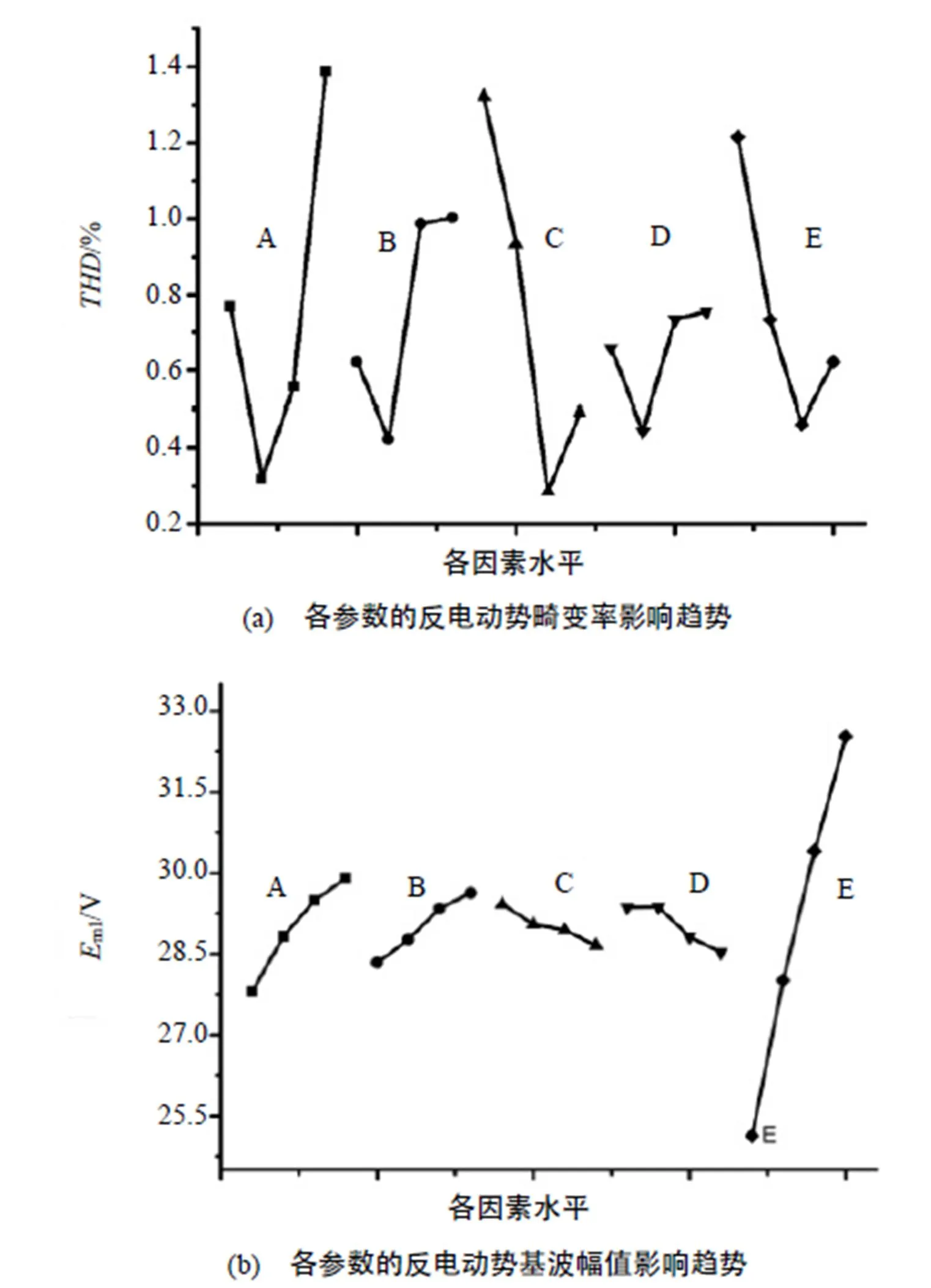
图4 影响趋势图

由表5和图4可知，5个参数中主磁极宽度和第一气隙宽度对反电动势波形畸变率THD的影响最大，第二气隙的宽度的影响和主永磁体与副永磁体的剩磁强度比例较为明显，副永磁体与主永磁体的宽度比例也有一定的影响。

主磁极宽度、副永磁体与主永磁体的宽度比例、第一气隙宽度、第二气隙的宽度对反电动势基波幅值的影响相对较小，可以忽略不计。而主永磁体与副永磁体的剩磁强度比例对反电动势幅值的影响最大。

以反电动势波形畸变率为目标函数，应选择_2、_2、_3、_2、_3组合为最优设计结果。但综合反电动势波形畸变率和基波幅值指标，对参数优化以增大反电动势基波幅值为主要目标，选择_4，其他参数以减小反电动势波形畸变率为主要目标。最后确定最优组合为_2、_2、_3、_2、_4，优化前后的为1.55%和0.192%，ml为24.0V和32.0V。

优化前后的反电动势波形如图5所示。

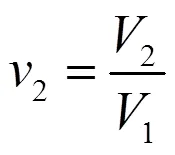
图5 优化前后空载反电动势波形的对比

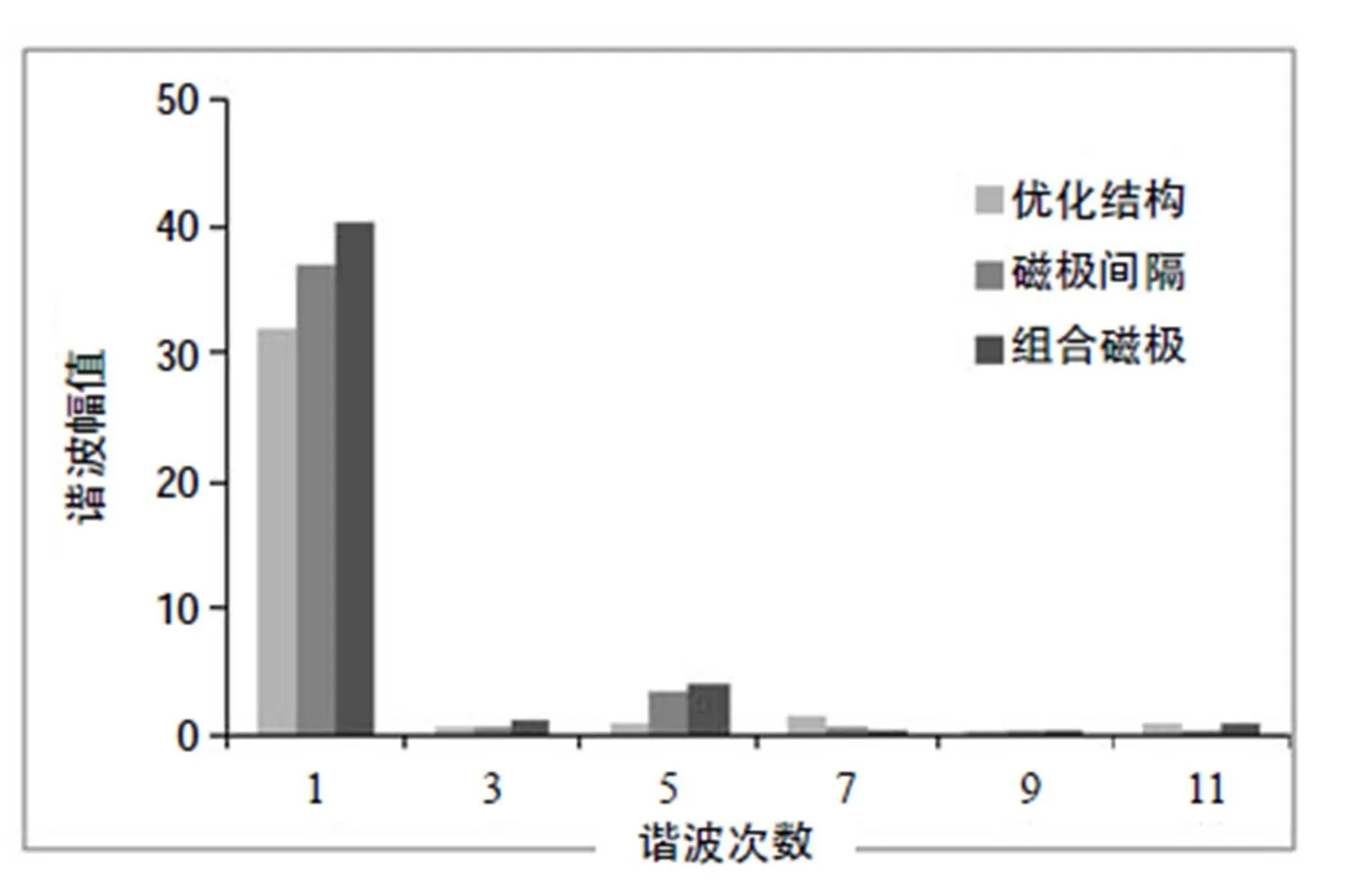
图6 不同优化方法的反电动势谐波对比

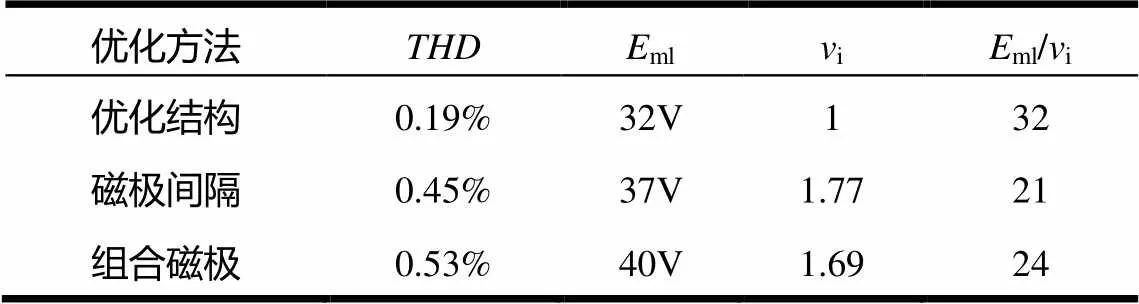
表6 不同优化方法的反电动势谐波分析

通过有限元仿真可得，磁极间隔和组合磁极的分别为0.45%和0.53%，计及间隔的组合磁极改进的反电动势波形相对其余两种优化方式有一定改善。在稀土永磁体用量减少的情况下，本文优化方案的反电动势幅值下降并不明显。

4 结论

本文针对六槽四极无刷直流电机的特性，提出了一种通过多块永磁磁极的不等剩磁和位置形状分布配合削弱反电动势谐波含量的方法。结合已有设计经验和前期仿真工作对电机各部分尺寸进行初选，利用田口法对电机的上述参数做进一步的优化设计，验证了此结构对反电动势优化设计的有效性，结果表明对无刷直流电机性能的提高有一定的指导意义。

[1] 吕鲁莹, 陈敏祥. 无刷直流电动机无位置传感器技术的新发展[J]. 微特电机, 2008, 36(9):56-59.

[2] 张勇, 程小华. 无刷直流电机与永磁同步电机的比较研究[J]. 微电机, 2014, 47(4):86-89.

[3] 谭建成. 永磁无刷直流电机技术[M]. 机械工业出版社, 2011, 282-283.

[4] 朱信舜, 林明耀, 刘文勇. 无刷直流电动机的正弦波电流驱动方法[J]. 微电机, 2011(11):51-55.

[5] Lee J H, Kim D H, Park I H. Minimization of higher back-EMF harmonics in permanent magnet motor using shape design sensitivity with B-spline parameterization[J]. IEEE Transactions on Magnetics, 2003, 39(3):1269-1272.

[6] Isfahani A H, Vaez-Zadeh S, Rahman M A. Using Modular Poles for Shape Optimization of Flux Density Distribution in Permanent-Magnet Machines[J]. IEEE Transactions on Magnetics, 2008, 44(8):2009-2015.

[7] Kasha A E, Sudhoff S D. Multi-objective design optimization of a surface-mounted modular permanent-magnet pole machine[C]// IEEE Power and Energy Conference at Illinois. IEEE, 2016.

[8] 朱德明, 严仰光. 离散Halbach永磁电动机气隙磁通密度特点及其空载电动势波形优化[J]. 电工技术学报, 2008, 23(11):22-27.

[9] Wang C F, Shen J X, Luk P C K, et al. Design issues of an IPM motor for EPS[J]. Compel International Journal of Computations & Mathematics in Electrical, 2011, 31(1):71-87.

[10] Chaithongsuk S, Nahid-Mobarakeh B, Caron J, et al. Optimal Design of Permanent Magnet Motors to Improve Field-Weakening Performances in Variable Speed Drives[J]. Industrial Electronics IEEE Transactions on, 2012, 59(6):2484-2494.

[11] 兰志勇, 杨向宇, 王芳媛,等. Taguchi方法在内嵌式正弦波永磁同步电机优化设计中的应用[J]. 电工技术学报, 2011(12):37-42.

[12] 徐涛, 赵世伟, 杨向宇,等. 基于田口法的磁通反向电机的优化设计[J]. 微电机, 2016, 49(2):6-9.

[13] 刘明基, 赵伟波, 赵海森,等. 基于Halbach阵列与组合型磁极相结合的表贴式永磁电机优化设计[J]. 电机与控制应用, 2016, 43(2):36-41.

[14] 杨玉波, 王秀和, 朱常青. 组合磁极削弱永磁同步电动机转矩脉动方法研究[J]. 电机与控制学报, 2013, 17(2):34-38.

[15] 黄晟, 任智杰, 黄科元,等. 永磁同步电动机气隙磁密优化方法研究[J]. 微电机, 2009, 42(10):26-28.

Optimization Design of BLDC Motor Based on Modular Polewith Several Parts

HE Zhirong, YANG Xiangyu, ZHAO Shiwei

(South China University of Technology, Guangzhou 510641, China)

In order to reduce the harmonic content of the Back-EMF, an novel rotor of BLDC motor model with modular pole and magnet segmentation which has several parts instead of one part per poleis presented. Base on the permanent magnet shape and materials, the sinusoidal degress of back-EMF and the amplitude of back-EMF were set as optimal objects. Then, the Taguchi method was introduced into the optimization of this model. By analyzing the effect of this BLDC motor’s performance caused by the variable of the optimal parameters, the optimal scheme was deduced. The results of the FEA verified the optimal performance of this model.

BLDC motor; modular pole; magnet segmentation; back-EMF

TM351

A

1000-3983(2018)03-0006-05

2017-06-07

何智荣（1991-），华南理工大学电力学院在读研究生，现从事特种电机磁路分析研究。