命题的否定与否命题问题归类解析
2018-06-02蒋满林
蒋满林
(福建省古田县第一中学 352200)
一、不等式型问题的否定
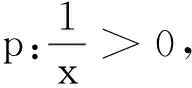
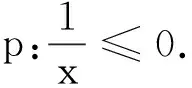

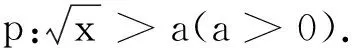
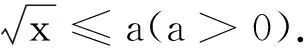
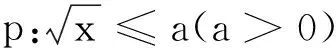
评注在数集中p的解集与¬p的解集具有补集的关系,可用真值表关系检验命题的对错.
二、等式型问题的否命题与否定
例3 原命题:若x2-5x+6=0,则x=2或x=3,请写原命题的否命题与命题的否定.
解析原命题的否命题:若x2-5x+6≠0,则x≠2且x≠3.
原命题的否定:若x2-5x+6=0,则x≠2且x≠3.
例4 请写出下列问题的非p.
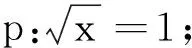
(2)已知p:x0=1.
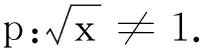
(2)¬p:x0≠1.
三、若p则q型问题的否定与否命题
例5 原命题 “若x2+ax+b≤0有非空解集,则a2-4b≥0”写出它的否命题与命题的否定.
解原命题的否命题: “若x2+ax+b≤0没有非空解集,则a2-4b<0”.
原命题的否定:“若x2+ax+b≤0有非空解集,则a2-4b<0”.
总结:一般地,“若p则q”型命题的否定与否命题有如下关系.
原命题:“若q则q”.
原命题的否命题:“若¬p则¬q”;
原命题的否定:“若p则¬q”.
评注这类问题是中学教学中最常见的一类问题,并且在写命题的否定时,p尽量不涉及全称量词或存在量词,如果有涉及则按第“四”种的方式作答.
四、条件p中含有(或隐藏有)全称量词或存在量词型问题的否定与否命题
例6 命题:若m>0,则方程x2+mx+1=0有实根,写出它的否命题与命题的否定并判断真假.
解否命题:若m≤0,则方程x2+mx+1=0无实根(假);
命题的否定:存在m>0,使方程x2+mx+1=0无实根(真).
例7 命题:若x>2,则1 解否命题:若x≤2,则x≤1或x≥3(假). 命题的否定:存在x>2,满足1 对于一般命题的否定,一些资料认为“若p则q”的否定是“若p则¬q”(只否定命题的结论),实际上这有时是不正确的,如果条件p中含有(或隐藏有)全称量词或存在量词(即开语句),那么否定时应考虑到条件p的范围. 评注一般地,对于含有一个量词的全称命题的否定,有下面的结论: 全称命题P:∀x∈M,p(x),它的否定¬P:∃x∈M,¬p(x); 特称命题P:∃x∈M,p(x),它的否定¬P:∀x∈M,¬p(x). 即有全称命题的否定是特称命题,特称命题的否定是全称命题. 参考文献: [1]黄树华.命题的“否定”与“否命题”辨析[J].语数外学习(数学教育),2013(01).
