动车组润滑油Fe光谱与铁量数据相关性的研究
2018-06-02屈晓龙
屈晓龙
(上海铁路局上海动车段,上海 201812)
0 引言
近年来,我国的高速铁路技术成果和建设成就在国际社会产生了重大影响,高速动车组的新实践、新发展极大地丰富和深化了人们对高速铁路技术水平、功能作用、发展模式、合作交流等方面的认识,而中国高速铁路更是走出了一条独具魅力的成功之路。据了解,目前我国铁路已投入运营的动车组达两千余组,每天开行动车组四千余列,研发、制造技术位于国际领先水平。
随着我国高速铁路的蓬勃发展,动车组的运行安全问题也得到了空前的重视。齿轮箱作为动车组传动系统的关键部件,尤其是作为一个易磨损部件,得到了广泛关注。一般,齿轮箱的失效方式主要有磨损、腐蚀和断裂等,其中,磨损失效是造成齿轮箱故障的主要原因之一。润滑油作为齿轮箱内的“血液”,起着润滑、密封、清洗、冷却和防腐等作用。此外,它还承担着记录齿轮箱磨损信息的重要任务— 润滑油内蕴含的大量机械杂质可作为监测齿轮箱运行状态及判断齿轮箱故障的重要依据。目前,对动车组齿轮箱润滑油的磨损分析方法主要有原子光谱分析法、铁谱分析法以及铁量分析法等。
传统观点认为,原子发射光谱分析法有效检测范围为亚微米级到微米级的小磨粒,而铁量分析法能够有效检测最高可达上百微米级的大磨粒,因而是独立的两种油液分析方法,对其数据相关性的研究较少。但是,Fe元素作为润滑油内的主要检测元素之一,两种分析方法均能对其进行有效检测。以上海动车段化验室(下文简称“化验室”)负责检测的CRH1型动车组齿轮箱润滑油为研究对象,借助SPSS软件采用数理统计分析法,就Fe元素在“光谱”与“铁量”检测数据上的相关性进行研究和探讨。
1 分析方法
1.1 旋转盘电极原子发射光谱法
本文中所采用的检测数据基于原子发射光谱原理,其原理是:在具备一定能量的光源(如电弧)中,物质在高温的作用下解离,不同组分的物质解离形成的原子分布在不同的能级,由于跃迁现象将产生不同的光辐射,即形成原子发射光谱。理论上该方法可用于检测任何状态的样品,且可实现多组分含量的同时检测,此外还具有灵敏、快速的特点,因此应用十分广泛。
1.2 铁量分析法
铁量仪是一种感应磁场变化的仪器,可以检测出油样中铁磁性物质的存在并以其浓度表示检测结果。其原理是:铁量仪有2个磁通计线圈,样品线圈(探测线圈)和参比线圈。在没有样品掠过时,2个线圈的磁场处于平衡状态;当把含有铁磁性物质的油样掠过探测线圈时,线圈内的磁通密度发生与铁磁性物质浓度正相关的变化,2个线圈之间的平衡被破坏产生相应电信号并被放大、过滤后显示为铁量浓度。铁量仪采用的是物理检测方法,与样品中铁磁性物质的含量更与其尺寸大小相关。
2 检测数据分析
基于两年来累积的CRH1型动车组齿轮箱润滑油液检测数据,光谱检测数据与铁量检测数据的单位均为ppm(10-6)。研究过程中收集了CRH1型动车组的共计2400个油样的“光谱”及“铁量”的对应检测数据。其中,由于光谱分析法(化验室所使用的光谱分析仪是美国斯派超SpectrOiL 120C型光谱分析仪,有效检测范围<10 μm)与铁量分析法(有效检测范围至mm级)对被测对象实施有效检测的尺寸范围不同,剔除因油样中含有大磨损颗粒导致光谱分析法失效的109个样品,有效研究对象总数为2291个,约占样本总数的95.5%。运用SPSS软件进行相关数理统计分析。
通过对数据的观察分析,可参考一元线性方程模型,假设:yi=α+βxi+εi。其中,yi表示某样品光谱检测数据值,xi表示该样品铁量检测数据值。根据一般线性回归分析方法,采用以下步骤对研究数据进行分析。
(1)绘制数据散点图(图1)
从图1可以看出光谱与铁量数据之间存在一定的线性相关关系。
(2)简单数据相关性分析
由表1可知Pearson简单相关系数(0.877)以及相关检验t统计量对应的p值(0.000,<0.05),可以看出表示两数据间具有较强的正相关关系,其中相关系数右上角的“**”表示相关系数在0.01的显著性水平下显著,则在该分析结果的基础上作进一步回归分析。
(3)线性回归分析

图1 散点图
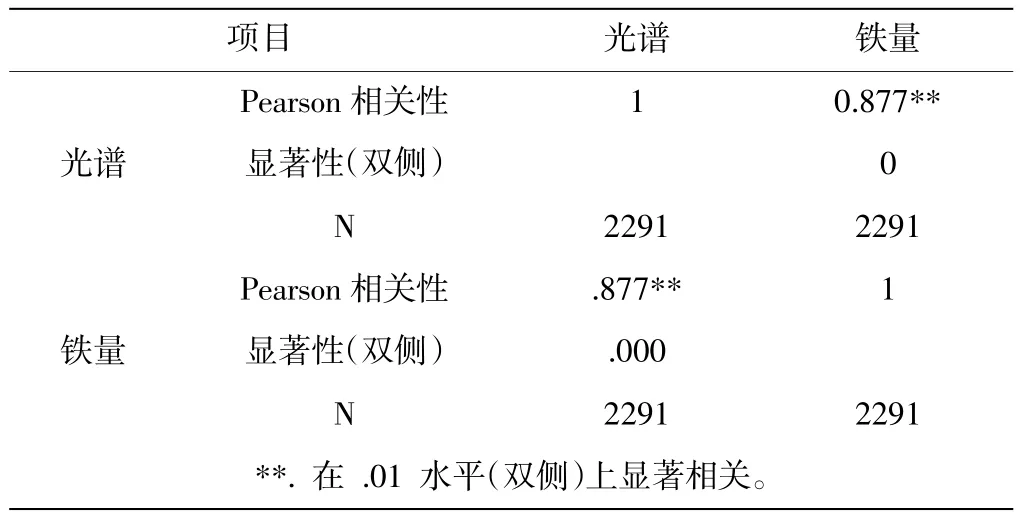
表1 简单相关性
表2给出了回归模型的拟合优度(R2)、调整的拟合优度(调整 R2)、估计标准差。从所得数据结果分析,该模型的判定系数以及调整后的判定系数分别为0.7693和0.7692,表示拟合优度较高,即收集的样品光谱检测数据76%以上的变动都可以通过假设的模型进行解释。

表2 回归模型的拟合优度评价
表3给出了假设模型的方差分析数据,其中Fe统计量为7631.521,对应的p值为0。则否定该模型非显著的可能性,即该模型的整体是显著的。

表3 方差分析表
由表4给出的分析结果可知,铁量(即解释变量x)与常数项的t统计量对应p值均远小于显著性水平0.05,此即表示在0.05的显著性水平下其均可满足t检验的相关要求。此外,由表4还可知所假设线性模型的常数项为4.660,斜率(即变量x的回归系数)为2.612,此时,可初步得出所假设模型方程为,即铁量数据值每增加A,其对应光谱数据值将增加2.612A。
上述所得模型初步方程未考虑随机扰动项,所以为进一步提高模型的可信度,绘制研究数据的标准化残差的P-P图(图2),由图2可知,研究数据形成的散点呈现在对角线附近,则可认为本研究中数据模型的残差基本服从正态分布。

表4 回归系数估计及其显著性检验
另外,根据图1呈现的散点可知,随着铁量数据值的增加,光谱数据值产生的波动范围明显加大,这表示随机扰动项在本次假设的分析模型中受异方差影响较大,应通过其他数学方法对模型作进一步修正以获得更加准确可靠的分析模型。

图2 标准化残差的P-P图
3 总结
通过运用数理统计的方法分析发现两种分析法在Fe元素的检测数据上存在较强的正相关性,并给出了初步分析后得到的模型方程。但通过图1可以看出,受限于数据来源,本次研究收集的数据比较集中,使得这种相关性具有一定局限性。此外,指出应借助其他数学方法修正模型以尽可能地减少异方差所产生的影响,而这些都还需要进一步收集数据后再进行深入研究分析。然而,结合生产实际,这种相关性的存在对于动车组齿轮箱润滑油的磨损分析仍具有重要意义。
(1)验证检测仪器运行状态。可以用于互相验证油样检测数据的准确性,进而判断分析仪器运行状态是否正常,避免产生错误检测数据,对齿轮箱故障的分析判断造成干扰;
(2)弥补技术上的不足。铁谱技术是一项十分重要的油液检测技术,可用于检测油液中的大磨损颗粒情况,由于其难度系数较大,暂时无法投入生产。但通过比对油样“光谱”与铁量数据是否与本文所述相关性存在明显差异可以在某种程度上间接判断油液中是否存在大磨损颗粒;
(3)提高经济效益。铁量分析法相对简便快捷,光谱分析法操作繁琐且成本相对较高,所以对该相关性进一步深入研究并修正后理论上可以利用铁量分析法进行部分油样的预检测,减少“光谱”作业量,降低生产成本。
[1]中国铁路总公司.高速动车组概论[M].北京:中国铁道出版社,2015.
[2]张锐,黄碧霞,何友昭.原子分析光谱[M].合肥:中国科学技术大学出版社,1991.
[3]丁国盛,李涛.SPSS统计教程[M].北京:机械工业出版社,2006.
[4]美国斯派超SpectrOil 120C型原子光谱分析仪使用说明书[R].
