粗糙表面形貌对滚动轴承油膜刚度的影响

雷春丽，李復宏，杨晓燕

(1.兰州理工大学数字制造技术与应用省部共建教育部重点实验室，甘肃 兰州 730050)(2.兰州理工大学机电工程学院，甘肃 兰州 730050)

滚动轴承广泛应用于旋转机械中，轴承的刚度对旋转机械的加工精度和动态性能有很大的影响[1]。对滚动轴承刚度的分析计算是对其支承的转子系统振动性能进行分析的基础。 轴承的刚度由滚动体与套圈滚道之间的接触刚度和润滑油油膜刚度共同组成[2-4]。目前主要基于Hertz刚度理论及其修正理论对接触刚度进行研究。近年来，一些研究人员在油膜刚度分析计算方面做了很多工作。吴昊等[5]对圆柱滚子轴承受力和弹性变形进行分析，在此基础上，引入弹性流体理论计算了轴承的径向刚度。杨静等[6]通过实验建立基于超声波的油膜刚度测试模型，揭示了油膜刚度与载荷的关系，并得出其对轴承刚度的影响规律。唐云冰[7]根据最小油膜厚度与接触载荷间的关系计算了轴承的油膜刚度。QIN等[8]在油膜厚度和弹性变形数值分析的基础上，研究了弹性流体动力学线接触的油膜刚度、接触体和合成刚度随不同的曲率半径、载荷和卷吸速度的变化规律。

实际上任何加工零件的表面都是粗糙表面，而粗糙表面对油膜厚度的形成有一定的影响。葛世荣等[9]对粗糙表面的分形特征进行了分析，并提出了粗糙表面的特征粗糙度概念。RAPETTO等[10]采用神经网络方法研究了表面粗糙度对实际接触面摩擦特性的影响。汪久根等[11]利用Fokker-Planck方程分析了表面粗糙度对滚动轴承振动的影响。张文明等[12]研究了径向轴承中气体薄膜在滑移效应和粗糙度耦合作用下的压强分布、承载能力等轴承特性，结果表明，由于表面粗糙度的影响，气体轴承压力分布、承载能力具有非线性特性，波动较明显。冯燕等[13]建立了粗糙表面热弹塑性接触法向刚度模型，分析了典型参数对结合部热弹塑性接触法向刚度的影响规律。弹流润滑的油膜厚度一般为0.10～1.00μm，而轴承滚动体与套圈接触表面经过光整加工后的粗糙度值一般在0.10μm左右[14]，因此表面粗糙形貌不仅对弹流润滑有较大的影响，而且对油膜刚度也有较大的影响。此外，油膜刚度的非线性变化会引起轴承-转子系统的低频振动，因此表面粗糙形貌对轴承-转子系统的振动也有显著的影响[15]。显然，在考虑轴承刚度问题时需要考虑油膜刚度，而上述研究分析很少涉及表面粗糙形貌对油膜刚度的影响。本文以弹流润滑理论和表面粗糙度理论为基础，在考虑轴承表面粗糙形貌的基础上，建立弹流润滑油膜刚度计算模型，研究表面粗糙形貌对滚动轴承油膜刚度的影响关系和规律。

1 滚动轴承几何模型

设滚动轴承内圈转动，外圈固定。滚动体与内圈接触处的当量曲率半径一般小于滚动体与外圈接触处的当量曲率半径，通常滚动体与外圈滚道之间的油膜厚度大于与内圈滚道之间的油膜厚度，故本文取滚动体与内圈滚道的接触区域作为研究对象。滚动轴承的结构简图如图1所示。

图1 滚动轴承几何模型

设内圈滚道的半径为R1，滚动体的半径为R2，外圈滚道的半径为R3，轴承内圈的转速为n，滚动体的圆心为O′，公转速度为nc，滚动体与内外圈的接触点分别为A和B,则滚动体与内圈滚道之间接触点的当量曲率半径为R=R1R2/(R1+R2)，内圈点A的速度为u1=2πR1n，滚动体A点的速度为u2=πR1R2n/(R1+R2)。

2 表面粗糙度理论模型

不管采用何种方法加工零件，其表面都不是绝对光滑的，零件表面都有各自的表面纹理[16]。表面纹理是指实际加工面与标准面的偏差，这种偏差来源于粗糙度、缺陷以及波纹度。为了表征这种特性，国际上通常采用表面粗糙度这一参数。图2为放大的滚动轴承内圈表面粗糙度形貌。

图2 放大的表面粗糙度形貌

任何复杂表面粗糙度形貌都是由许多不同形状的微凸峰和微凹谷组成，并且都可以用多个正弦信号进行叠加解析。这里以[-1 +1]区间的正弦信号来模拟分析表面粗糙度对油膜刚度的影响。设表面粗糙度函数为

(1)

式中：x的无量纲化参数在[-1,+1]区间上取值；DA为粗糙度幅值；lf为粗糙度波长。

3 弹流润滑油膜刚度计算模型

3.1 弹流润滑基本方程

Reynolds方程采用文献 [17]中非牛顿流体动压分布规律的广义Reynolds方程，可表示为

(2)

式中:ρ为润滑油的密度；p为润滑油压力；h为油膜厚度；us为润滑油卷吸速度，us=(u1+u2)/2；η为润滑油动力黏度。

考虑粗糙度的线接触油膜厚度方程为

(3)

式中：h0为中心膜厚；v(x)为变形方程；r(x)为表面粗糙度函数。

(4)

式中：x0、xe分别为计算域的起点和终点坐标；p(s)为距坐标原点s处的压力；E为两接触表面材料的综合弹性模量。内圈滚道表面、滚动体表面的弹性模量分别为E1,E2，其Poisson比分别为υ1,υ2，则

(5)

黏压关系采用Roelands黏压方程：

(6)

式中：η0为p=0时的润滑油黏度；z为常数；p0为压力黏度系数。

密压关系采用Dowson-Higginson密压方程：

(7)

式中：ρ0为p=0时润滑油的密度。

载荷平衡方程为

(8)

式中：w为单位长度上的载荷。

3.2 油膜刚度计算模型

根据刚度的定义可知：

(9)

式中：kf为接触区的油膜刚度；Δw为接触区的分布载荷；δ为接触区油膜压缩变形量。

根据图3所示的线接触弹流润滑理论建立滚动轴承的线接触模型。

图3 接触区载荷与油膜厚度

由于线接触区油膜的压缩变形量可用Δh表示，因此公式(9)可变形为[8]

(10)

式中：b为接触区长度。

3.3 数值计算方法

为了便于分析和求解，并改善计算过程的数值稳定性，需对所建数学模型进行无量纲化处理，定义无量纲化参考量如下：

式中：pH为最大Hertz压力；u为流体速度；α为黏压系数。

联立Reynolds方程、油膜厚度方程、黏压方程、密压方程、载荷平衡方程，通过Newton-Raphson迭代法[18]进行计算。求解时由于直接给出较粗糙的膜厚形状，光滑表面的Hertz压力解与真解的差距较大，容易造成计算不收敛，因此采用逐步增加粗糙度幅值的方法来实现较大粗糙度的弹流节点。收敛判据是Hertz压力的误差小于0.001。

4 数值仿真结果及分析

数值计算中使用的各物性参数如下：润滑油的环境黏度η0=0.02Pa·s，压力黏度系数p0=1.96×108，两接触表面的综合弹性模量E=2.20×1011Pa，速度us=1.5m/s，载荷W=1.0×105N/m，当量曲率半径为R=0.02m，无量纲化初始环境密度为ρ0=1，材料参数为G=5 000，Z=0.68，入口参数x0=-2.0，出口参数xe=1.5。数值计算过程中若粗糙度幅值DA大于0.15μm会出现计算结果不收敛情况，在这种情况下随着粗糙度幅值继续增大油膜压力也增大，可能会引起油膜破裂，使接触面磨损较快，从而降低轴承的使用寿命，故本文的粗糙度幅值DA最大取0.16。波长太小会导致最小油膜厚度太小，波长太大会引起最大压力减小，故波长取值在0.10～1.00μm之间。

4.1 压力和膜厚分布

图4、图5分别为表面粗糙度幅值DA为0时的油膜厚度和压力分布图。由图4、图5滚动轴承弹流润滑数值解可以看出，在粗糙度幅值DA为0的情况下，膜厚出现明显的颈缩现象，压力分布出现了明显的第二压力峰，表现出经典的弹流润滑特性。此结果与文献[19]中给出的弹流润滑特性结论和变化趋势(图4、图5中左上角小图)一致。

图4 弹流润滑油膜厚度分布

图5 弹流润滑压力分布

4.2 幅值对油膜压力和膜厚分布的影响

图6为不同粗糙度幅值下接触区膜厚变化的分布图，从图可以看出，整体而言膜厚随粗糙度幅值的变化不大。此外，在表面凸峰处膜厚随粗糙度幅值的增大有所减小，表面凹陷处膜厚随粗糙度幅值的增大有所增大。图7为不同粗糙度幅值下接触区压力变化分布图，从图可以看出，接触区压力变化十分明显，一定范围内，表面凸峰处压力随粗糙度幅值的增大而增大，表面凹陷处压力随粗糙度幅值的增大而减小，第二压力峰也随粗糙度幅值的增大而增大。这是因为粗糙度幅值增大，表面凸峰处对润滑油的“阻碍”作用和表面凹陷处对润滑油的“储存”作用增强，润滑油阻塞导致膜厚减小、压力增大，润滑油存储导致膜厚增大、油膜压力减小。

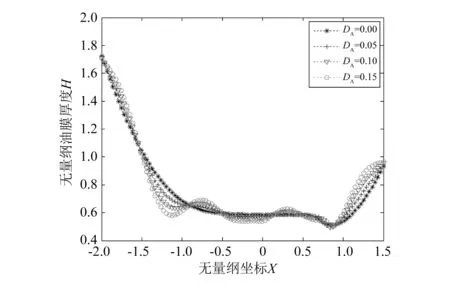
图6 不同粗糙度幅值下的膜厚分布

图7 不同粗糙度幅值下的压力分布

4.3 波长对油膜压力和膜厚的影响

图8为粗糙度幅值DA=0.05μm(幅值取得太小波长影响不明显，太大会出现不收敛情况)时不同波长下接触区膜厚分布。从图可以看出，油膜的变化范围随波长的增大而减小，同样膜厚的变化频率也随波长的增大而减小，并越来越接近光滑表面下的膜厚变化。这是因为波长增大导致表面凸峰和凹陷变缓，达到一定值时油膜全部均匀覆盖，使膜厚对波长变化不敏感。

图9为粗糙度幅值DA=0.05μm时不同波长下接触区压力分布，从图可以看出，随着波长的增大油膜压力的变化幅度、变化频率均减小，这是因为随着波长的增大，表面凸峰、凹陷处对润滑油“阻碍”、“储存”作用减弱的缘故。当波长趋于无穷大时，接触面在滚动方向变成了一平面，接近为接触面光滑的弹流模型。

图8 不同波长下的膜厚分布

图9 不同波长下的压力分布

4.4 粗糙度对油膜刚度的影响

图10为不同粗糙度幅值下油膜刚度的变化分布图，从图可以看出，油膜刚度随粗糙度幅值增大呈现非线性变化，油膜刚度的最大值位于接触区中心附近，随幅值增大主峰与第二峰逐渐融合，并向入口区偏移，同时在出口区附近有峰值出现；粗糙度幅值在DA=0.10μm附近变化时油膜刚度发生了显著的变化。

图11为粗糙度幅值DA=0.05μm时不同波长下的油膜刚度分布图。从图可以看出，油膜刚度变化的频率随波长的增大而减小，变化幅度随波长的增大先增大后减小，波长在lf=0.50μm上下变化时油膜刚度变化十分明显。

从图10和图11不难看出，与光滑表面油膜刚度的变化相比，一定程度粗糙表面的油膜刚度性能优于光滑表面油膜刚度性能。因此，粗糙度幅值和波长控制在一定的范围内，有助于减弱由于油膜刚度非线性变化引起的轴承低频振动。

5 结论

图10 不同幅值下的油膜刚度分布

图11 不同波长下的油膜刚度分布

通过研究线接触弹流润滑下表面粗糙度对滚动轴承油膜刚度的影响可知，表面粗糙度的变化会引起油膜厚度、油膜压力和油膜刚度的变化。得到的具体结论如下：

1)随着表面粗糙度幅值的不断增大，油膜厚度的变化幅度不大，但油膜压力变化十分明显，一定范围内，表面凸峰处与表面凹陷处对油膜压力的影响截然相反。

2)在表面粗糙度幅值一定的情况下，随着波长不断增大，膜厚的变化范围和变化频率都在减小，与此同时，油膜压力变化幅度和变化频率也表现出了同样的规律。

3)表面粗糙度幅值和波长与油膜刚度呈非线性关系。粗糙度幅值变化对油膜刚度的影响大于波长变化所带来的影响。粗糙度幅值在DA=0.10μm附近和波长在lf=0.50μm附近变化时对油膜刚度有显著的影响。另外，粗糙度幅值控制在0.10μm左右和波长控制在0.10～0.80μm之间，有助于减弱由于油膜刚度非线性变化引起的轴承低频振动。

参考文献：

[1] ZHANG Weigang, GAO Shanghan, LONG Xinhua, et al. Analysis of nonlinear dynamics on machine tool spindle-rolling bearing[J]. Journal of Vibration and Shock，2008,27(9)：72-75.

[2] 吴明星, 吴维, 胡纪滨, 等. 考虑自旋的高速角接触球轴承的油膜刚度计算[J]. 振动与冲击，2014,33(10):38-42.

[3] 陈斌, 陈剑, 董玛莉, 等. 基于点接触热弹流润滑的油膜刚度建模分析[J]. 润滑与密封, 2013,38(8):70-75.

[4] ZHANG Hao, ZHAI Jingyu, HAN Qingkai, et al. Dynamics of a geared parallel-rotor system subjiected to changing oil-bearing stiffness due to external loads[J]. Finite Elements in Analysis and Design, 2015,106:32-40.

[5] 吴昊, 安琦. 弹流润滑圆柱滚子轴承径向刚度计算[J]. 轴承, 2008(1): 1-4.

[6] 杨静, 杨亮, 杨园鉴, 等. 圆柱滚子轴承的刚度计算[J]. 中国科技论文, 2014,9(8):897-901.

[7] 唐云冰. 航空发动机高速滚动轴承力学特性研究[D]. 南京:南京航空航天大学, 2005.

[8] QIN Wenjie, CHAO Jie, DUAN Lunjing. Study on stiffness of elastonhydrodynamic line contact[J]. Mechanism and Machine Theory,2015,86:36-47.

[9] 葛世荣, TONDER K. 粗糙表面的分形特征与分形表达研究[J]. 摩擦学学报, 1997,17(1):73-80.

[10] RAPETTO M P, ALMQVIST A, LARSSON R, et al. On the influence of surface roughness on real area of contact in normal, dry, friction free, rough contact by using a neural network[J]. Wear, 2009, 266: 592-595.

[11] 汪久根, 王庆久, 章维明. 表面粗糙度对轴承振动的影响[J]. 轴承, 2007(1):23-25,30.

[12] 张文明, 孟光. 随机表面粗糙度对MEMS径向气体轴承性能影响[J]. 振动工程学报, 2012,25(1):60-63.

[13] 冯燕, 俞小莉, 刘震涛. 基于热弹塑性理论的法向接触刚度分形模型[J]. 浙江大学学报(工学版),2015,49(8):1553-1558

[14] 周敏, 燕阳, 林颖. 滚动轴承电化学机械光整加工[J]. 冶金设备, 2003(6):51-53.

[15] 张柏林, 王飞, 许泽怀. 轴承油膜刚度非线性变化导致低频振动的研究[J]. 湖南电力, 2002,22(1):13-15.

[16] KALPAKJIAN S, SCHMID S R. Manufacturing engineering and technology[M]. Englewood: Prentice-Hall, 2001.

[17] 杨沛然, 温诗铸. 线接触热弹流润滑膜的最小膜厚公式[J]. 青岛建筑工程学院学报, 1991,12(3)：1-8.

[18] HUANG Ping, WEN Shizhu. Sectional microealstohydro-dynamic lubrication[J]. Trans. ASME Journal of Tribology,1993,115(1):148-151.

[19] DOWSON D, HIGGINSON G. The effect of material properties on the lubrication of elastic rollers[J]. Journal of Mechanical Engineering Science,1960,2(3):188-194.