Discussion on“Empirical methods for determining shaft bearing capacity of semi-deep foundations socketed in rocks”[J Rock Mech Geotech Eng 6(2017)1140-151]

Ergin Arioglu,Pinar Toru Seker,Hasan Burak Gokce

Yapı Merkezi Construction and Industry Inc.,Istanbul,Turkey

1.Introduction

First of all,the discussers wish to congratulate the authors of the article“Empirical methods for determining shaft bearing capacity of semi-deep foundations socketed in rocks”,S.Rezazadeh and A.Eslami,for their invaluable contributions to the literature on determining shaft bearing capacity of semi-deep foundations socketed in rocks.The data set(number of the data,n=106)in the aforementioned study is a substantial source for the researchers involved in the design of rock-socketed piles for any further studies.

Piles socketed into rock masses are broadly utilized to carry huge loads transmitted from long-span bridges and high-rise buildings.The rock-socketed piles must be designed to support the huge imposed loads safely and limit settlement/differential settlement to a permissible level.Pile lengths larger than 70 m,diameters up to 3 m and project loads exceeding 50 MN are readily realized.The performances of rock-socketed piles at design loads are mainlygoverned by the shear resistance and the base resistance developed at the interface between the concrete shaft/base and the surrounding rock mass.According to the findings derived from numerous in situ pile load tests,magnitude of shear resistance depends on various parameters,such as strength and stiffness of rock mass,socket roughness,weathering degree,and pressure imposed on the socketed rock owing to fluid concrete placement(Johnston et al.,1992;Haber field and Collingwood,2006).As a result,socket performance is subjected to the significant variation from one site to another,even in the same geological setting.

Generally speaking,the design approaches for determination of ultimate capacities in shear/base resistance are still based upon empirical regressions obtained from the back analysis of in situ rock-socketed pile load tests.Most of these regression analyses are expressed in terms of only uniaxial compressive strength(UCS)of intact rock(σrc)(Arioglu et al.,2007).In the engineering practice,it is well known that the inherent conservation of these approaches usually results in unnecessarily long sockets and uneconomical solutions(Haber field and Collingwood,2006).

The discussers would like to make the following additional comments and contributions to the study of Rezazadeh and Eslami(2017).

First,a new comprehensive set of data(n=178)is compiled by adding a data set collected by Arioglu et al.(2007)(n=72)to the data set presented in Rezazadeh and Eslami(2017)(n=106).Then,the compiled data set is evaluated regardless of the variation in lithology/strength.

Second,rock mass cuttability index(RMCI)is correlated with shaft resistance(rs)to predict the shaft resistance of rock-socketed piles.In the literature,RMCI is used to determine the penetration rate(i.e.advance rate of mechanized tunneling machinery/drilling machinery/tunnel boring machines)in excavation engineering.In other words,the RMCI parameter is directly related to the rock quality designation(RQD)defining the jointing density of the rock mass and the UCS of intact rock(σrc).In addition,all derived regression models are validated through their prediction capacity.

2.Derived regression equations

2.1.rs=f(σrc)

In geotechnical literature,empirical relationships between the shaft resistance(the ultimate unit side resistance)rsand UCS of intact rock(σrc)have been proposed by many authors(Horvath and Kenney,1979;Rowe and Armitage,1987;Kulhawy et al.,2005;Haber field and Collingwood,2006).On close examination of these relationships,the common mathematical model can be written as(Dai et al.,2017;Rezazadeh and Eslami,2017):

whereαandβstand for empirical factors derived from back analysis of rock-socketed pile load tests.The factorαvaries from 0.15 to 0.6 andβis in the range of 0.5-1.The magnitude ofαdepends largely on the socket roughness.For example,for piles with very rough interface between the concrete shaft and the rock mass,α value yields 0.6.MMFis the mass modulus factor,which sometimes terms reduction factor.Its value is related to the following function:

In other words,theMMFvalue can be determined from the ratio between rock mass elastic modulus(Em)and intact rock elastic modulus(Er)for a given rock quality designation(RQD).This index was developed to provide a quantitative measure of jointing degree of rock mass from drill core logs.For instance,for intact rock without joint,RQD takes avalue of 100%as expected,Em/Erratio is 1 and the MMF value is also obtained as 1.For a weak rock mass withRQD=20%,Em/Erratio can be approximated as 0.04,and then MMF can be predicted to be approximately 0.45.As noticed,in the case of heavily jointed,weak and weathered rock mass,the shaft resistance(rs)is significantly reduced.

It is worthy to mention herein that according to an international data base containing 72 in situ pile load tests,using RQD values for MMF prediction on the basis of presentRQD=f(Em/Er)modulus ratio relationships can be said to be inadequate,resulting in underestimating shaft resistance.In order to correctly incorporate RQD into design process,both “RQD-modulus ratio”and “RQD-roughness”relationships must be considered(Wainshtein et al.,2008).

Carter and Kulhawy(1992)and Salgado(2008)recommended design check to compare the allowable side resistance of the shaft socket(rs/factor of safety(FS))to the side bond-cohesion-strength of the pile materials(concrete,grout or cement paste),which is determined by a value of 5%of the characteristic compressive strength of the pile material(fc).The lower value would control,unless in situ pile test provided otherwise(Kulhawy et al.,2005).

The cohesion value of concrete(c)can be approximated by the following equations based on the Mohr-Coulomb failure criterion(Arioglu et al.,2006):

whereftis the direct tensile strength,ftspis the splitting tensile strength,λis the factor for converting splitting tensile strength(ftsp)to direct tensile strength(ft)and is adopted to equal 0.9,andfcis the characteristic strength (in MPa) of concrete material(φ150 mm × 300 mm cylinder samples).For example,whenfc=30 MPa,the cohesion value of this concrete can be calculated as

Assuming the FS value of 3 against the concrete bond,the allowable cohesion value can be estimated as 1.56 MPa.Checking this value with 0.05fcrule,one obtains 1.5 MPa.As can be noticed,the cohesion values derived from two approaches appear agreeable.In addition,it should be stated that cases of sockets exceeding the concrete bond strength with lower concrete strength and lower FS can exist in the field,but all these cases manifested about theacceptable behavior of the concrete since concrete is confined in a socket and reinforced(Kulhawy et al.,2005).

Table 1Detailed information on data set used in the regression analyses and results.

In order to increase the number of data set(n=178)for prediction of shaft resistancersand average UCS of intact rock(σrc),the data cited in p.203-204 of Arioglu et al.(2007)were combined with the data set represented in Rezazadeh and Eslami(2017).Resulting equations obtained from the regression analysis associated with informative explanations are tabulated in Table 1.Furthermore,it should be herein reminded that in the study under consideration,the regression equation derived from data set 1 does not provide information on the number of outliers in the data.On the other hand,in this discussion,the comprehensive data set(data sets 1+2)contains 178 data and all of them were utilized in the regression analysis without any “outlier”selection.In other words,the resulting equation(Fig.1)covers broad lithology/strength spectrum.In the same figure,the equation proposed in Kulhawy et al.(2005)is also plotted for the sake of comparison.It is obvious that the Kulhawy et al.(2005)equation and the proposed equation are in a good agreement for the range between 0.15 MPa and 25 MPa.The average “predicted value/observed value(P/O)”ratio is 0.8±SD,whereSDstands for the standard deviation and it is equal to 0.5.TheP/Oratio of 1 corresponding to “center”is equal to 19 out of 178 which is around 11%of the total data.Furthermore,to verify the predictive capacity of the equation derived in this study,theP/Oratio of shaft resistance was displayed associated with statistical parameters in Fig.2.TheP/Oratio of 1 corresponding to “center”is equal to 65 out of 178 which is 37%of the total data.Keeping the previously mentioned several factors having influence of shaft resistance in mind,this figure appears to be quite satisfactory.

2.2.rs=f(RMCI)

RMCI is an index in rock mechanics to predict the penetration rate/advanced rate related to the rock mass capacity(RQD and UCS)in mechanized tunneling machinery such as road headers and hydraulic breakers.This index has been used since 1985,and proposed in Bilgin et al.(2002,2013)with a new proposed correlation which is also used in this discussion(Table 2).The importance of this index is directly related to the parameters on the calculation of the index itself.RMCI is a function ofσrcand RQD.It should be mentioned here that RQD is a parameter measuring the jointing degree of rock mass.That is why,in this section,as a first time in the literature,it is investigated in a considerable detail that whether the RMCI parameter can be used to predict shaft resistance in rocksocketed piles or not.

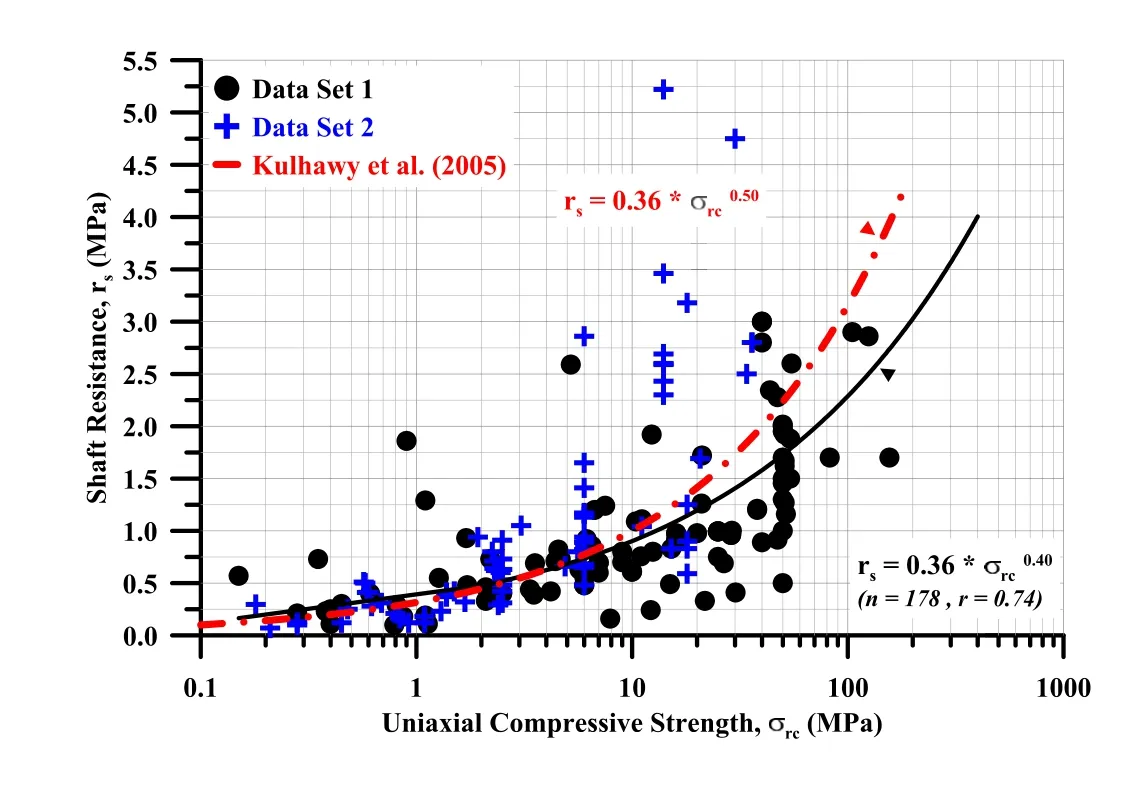
Fig.1.Variation of the shaft resistance(rs)and UCS(σrc)for combined data set(data sets 1+2).The red continuous curve represents the equation derived from Kulhawy et al.(2005),corresponding to normal rocks socketed for drilled shafts.

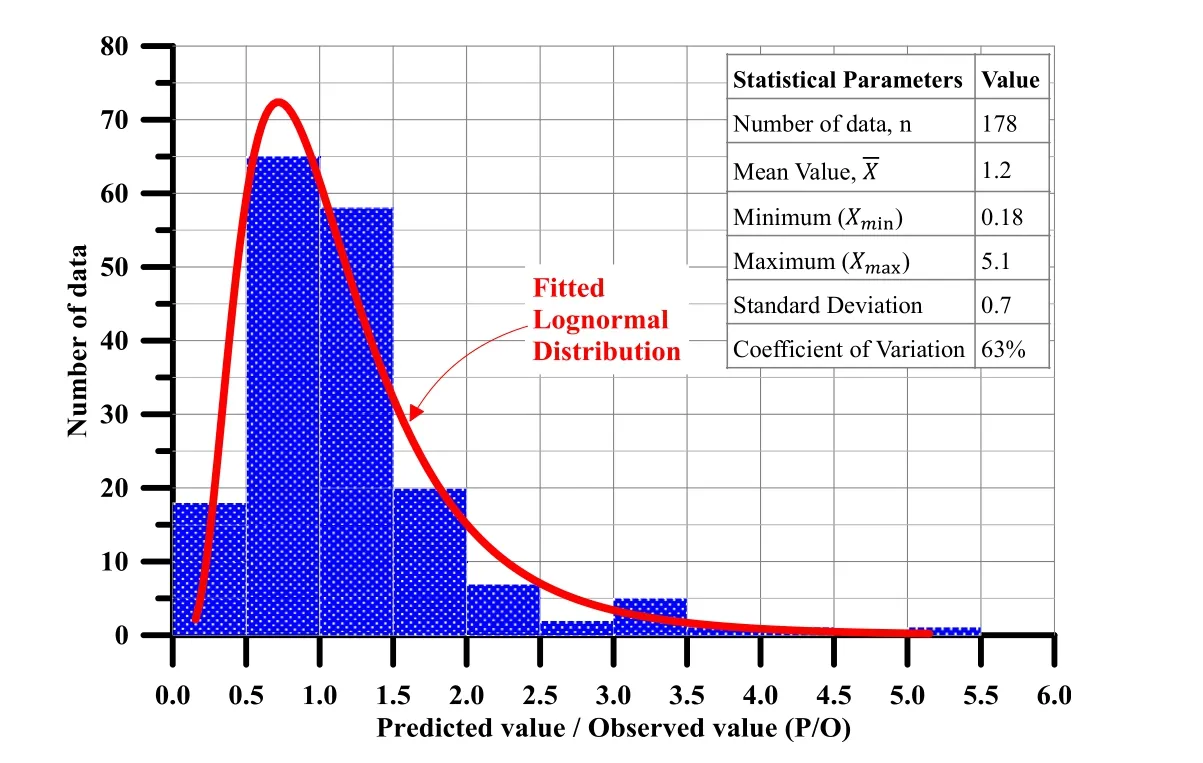
Fig.2.Distribution of verification on prediction capacity(predicted/observed shaft resistance values)for the combined data set(data sets 1+2)associated with the statistical parameters.

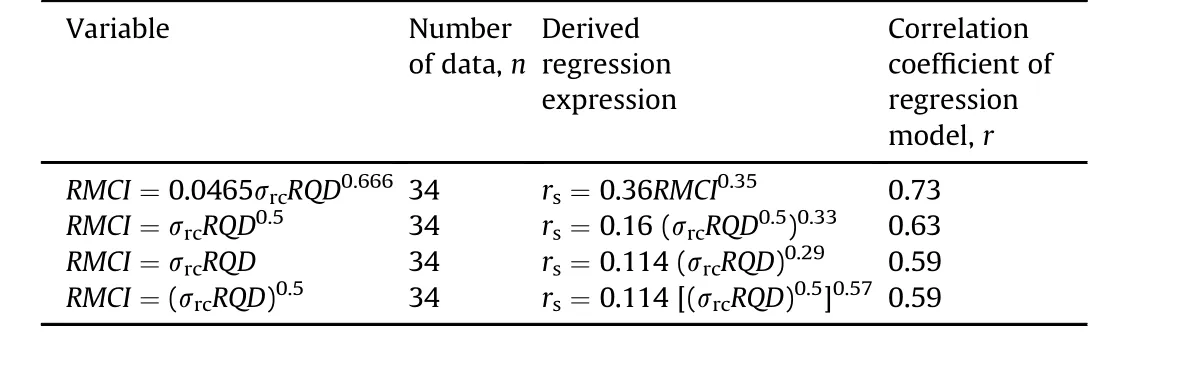
Table 2Proposed regression models for the relationship between shaft resistance(rs)and RMCI based on different variables.

Fig.3.Best fitted regression model between shaft resistance(rs)and RMCI.

In this study,the authors would like to propose a new empirical prediction equation resulting from a regression analysis between shaft resistancersand RMCI,by using the data taken from Rezazadeh and Eslami(2017)(see Table 2 and Fig.3).In the regression analyses,possible variables in terms of RQD andσrcare also tried to predict the relationship betweenrsand RMCI which is a function of RQD andσrc.However,the best fitted variable is the one proposed in Bilgin et al.(2002,2013)with a coefficient of correlationr=0.73.As can be seen in Fig.3 between the shaft resistance(rs)and RMCI parameter,there is a powered relationship represented in a semi-log scale.The mean predictive capacity(P/O)ratio of the mentioned equation is calculated as 1.21 withSD±0.96.TheP/Oratio of 1 corresponding to “center”is equal to 15 out of 34 which is 44%of the total data.Based on this estimated capacity value,it can be said that the prediction ability of the proposed empirical equation betweenrsand RMCI of this study is fairly good.In other words,RMCI parameter appears as a promising index in the estimation of shaft resistance in the socketed-pile design.

3.Conclusions

In order to increase the number of data set(n=178)for prediction of shaft resistancersand average UCS of intact rock(σrc),the data cited in p.203-204 of Arioglu et al.(2007)were combined with the data set represented in Rezazadeh and Eslami(2017).The prediction capacity of the resulting equation obtained from the regression analysis was found to be in a good agreement with the observed data(Fig.2).The proposed empirical equation in this study comprises a wider range of UCS(0.15 MPa＜ σrc＜ 156 MPa)and various rock types(Fig.1).

The prediction of the shaft resistance in the rock-socketed piles is also investigated in this discussion with a different parameter named RMCI instead of UCS(σrc).RMCI is a function of RQD andσrcthat also have been used in the literature to predict the penetration rate/advanced rate of road headers and hydraulic breakers in mechanized tunneling machinery.In this discussion,the relationship betweenrsand RMCI is investigated and a new empirical equation is also presented(Fig.3).The prediction capacity of the aforementioned equation is also found to be in a fair good agreement with the presented data in Rezazadeh and Eslami(2017).Since the RMCI is a promising parameter in the prediction of shaft resistance,the researchers in the rocksocketed pile design area should consider this parameter in the further investigations.

Conflict of interest

The authors wish to confirm that there are no known conflicts of interest associated with this publication and there has been no significant financial support for this work that could have influenced its outcome.

Acknowledgements

This discussion paper was made possible by the support of Yapı Merkezi Construction and Industry Inc.,Istanbul,Turkey.The opinions expressed in this paperare those of the authors and do not necessarily reflect the views of those acknowledged here.

Arioglu N,Girgin ZC,Arioglu E.Evaluation of ratio between splitting tensile strength and compressive strength for concretes up to 120 MPa and its application in strength criterion.ACI Materials Journal 2006;130(1):18-24.

Arioglu E,Yılmaz AO,Tuncdemir H.Socketed bored piles into rock mass-technical sheets and solved problems.Istanbul,Turkey:Evrim Publisher;2007(in Turkish).

Bilgin N,Dinçer T,Çopur H.The performance prediction of impact hammers from Schmidt hammer rebound values in Istanbul metro tunnel drivages.Tunnelling and Underground Space Technology 2002;17(3):237-47.

Bilgin N,Çopur H,Balci C.Mechanical excavation in mining and civil industries.CRC Press;2013.

Carter JP,Kulhawy FH.Analysis of laterally loaded shafts in rock.Journal of Geotechnical Engineering 1992;118(6).https://doi.org/10.1061/(ASCE)0733-9410(1992)118:6(839).

Dai G,Salgado R,Gong W,Zhu M.The effect of sidewall on the shaft resistance of rock-socketed piles.Acta Geotechnica 2017;12(2):429-40.

Haber fi eld C,Collingwood B.Rock-socketed pile design and construction:a better way?Proceedings of the Institution of Civil Engineers Geotechnical Engineering 2006;159(3):207-17.

Horvath RG,Kenney TC.Shaft resistance in rock socketed drilled piers.In:Proceedings of the symposium on deep foundations.Reston,USA:American Society of Civil Engineers(ASCE);1979.p.182-214.

Johnston IW,Haber field CM,Sands M.Side resistance of piles in weak rock.In:Piling:European practice and worldwide trends.London,UK:Thomas Telford;1992.p.52-8.

Kulhawy FH,Prakoso WA,Akbas SO.Evaluation of capacity of rock foundation sockets.In:Chen G,Huang S,Zhou W,Tinucci J,editors.Proceedings of the 40th US symposium on rock mechanics.Anchorage,USA:ARMA;2005.

Rezazadeh S,Eslami A.Empirical methods for determining shaft bearing capacity of semi-deep foundations socketed in rocks.Journal of Rock Mechanics and Geotechnical Engineering 2017;9(6):1140-51.

Rowe RK,Armitage HH.A design method for drilled piers in soft rock.Canadian Geotechnical Journal 1987;24(1):126-42.

Salgado R.The engineering foundations.New York,USA:McGraw-Hill Companies,Inc.;2008.

Wainshtein I,Hatzor YH,Doktofsky M.Does shaft resistance of piles in rock scale with RQD?.In:Proceedings of the 42nd US rock mechanics symposium and 2nd US-Canada rock mechanics symposium.San Francisco,USA:American Rock Mechanics Association(ARMA);2008.p.1-11.