降雨对花岗岩残积土边坡孔压及稳定性影响

2018-06-01林鸿基许旭堂吴能森

井冈山大学学报(自然科学版) 2018年2期

林鸿基，许旭堂，徐祥，黄浩，吴能森

(福建农林大学交通与土木工程学院，福建，福州 350108)

0 引言

花岗岩残积土是花岗岩经物理风化和化学风化后残留在原地的碎屑物，在我国的闽、粤、桂、湘、赣等省分布较为广泛。其出露面积，在闽、粤两省达到30%～40%，桂、湘、赣三省达到10%～20%[1]。福建地区以山地和丘陵地貌为主，又属亚热带海洋性季风气候区，雨量充足，因此福建省花岗岩残积土滑坡灾害频发，特别是雨季滑坡灾害更为频繁[2]。

影响土质边坡稳定性的因素有很多，其中降雨入渗作用是最主要的因素。很多学者针对土质边坡的降雨入渗开展了研究，通过数值模拟和模型试验，分析降雨强度、降雨持时、土体饱和渗透系数、初始含水率等对边坡渗流场及稳定性的影响[3-10]。

研究表明：非饱和土质边坡在降雨入渗条件下，孔隙水压力增大，基质吸力降低，从而降低土体抗滑力，最终导致边坡失稳破坏。花岗岩残积土除了具有非饱和土特点外，在水的浸泡下还具有软化特性，致使抗剪强度指标降低[11]，因而降雨入渗对花岗岩残积土边坡的不利影响更甚。拟针对一个花岗岩残积土实际边坡的简化模型，基于非饱和渗流理论和Bishop条分法公式，利用Geo-Studio软件分析在均布型、前峰型、中峰型、后峰型4种降雨模式下，花岗岩残积土边坡孔隙水压力及边坡稳定安全系数的变化规律。

1 非饱和土渗流及稳定性分析理论

1.1 非饱和土渗流理论

由于非饱和土边坡在降雨入渗过程中，土体的含水率、饱和度随时间而变化，所以其入渗水流属于非稳定流或瞬态流。假定降雨过程中，坡体上没有施加外荷载，且非饱和区气压连续不变，则二维非稳定渗流的控制方程为[12-13]：

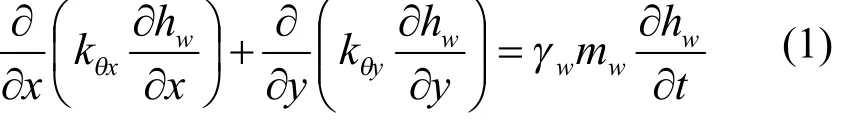
式(1)中：分别为x、y方向的非饱和渗透系数，分别为土体中的总水头、水的容重、时间，为与基质吸力变化有关的水的体积变化系数，即是土水特征曲线斜率的绝对值。

非饱和渗透系数与饱和区渗透系数的关系可采用A.F.Averjanov的推荐式[12]，即

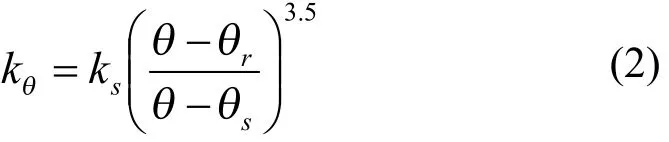
其中，分别为体积含水率、剩余体积含水率、饱和体积含水率，可由土水特征曲线得到。

1.2 非饱和土边坡稳定性

针对非饱和土，Fredlund等[13]提出了饱和-非饱和状态下的Mohr-Coulomb准则：非饱和土抗剪强度由有效粘聚力、外荷引起的净应力产生的剪阻力和内部应力产生的剪阻力三部分组成，给出非饱和土抗剪强度计算公式如下：

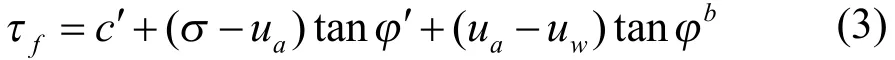
式(3)中：分别为土体的有效粘聚力、有效内摩擦角、吸力摩擦角，分别为总应力、孔隙水压力、孔隙气压力。

与式(3)对应，将 Bishop条分法应用于非饱和土，边坡稳定安全系数的简化计算公式为：

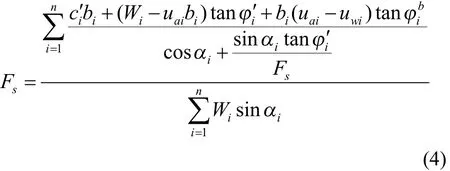
式(4)中：为土条宽度，为土条重力，为土条底面与水平面的夹角，n为划分的土条数。

2 降雨分析模型

2.1 降雨模式

降雨是一个随机过程，为便于分析，需要对实际降雨过程进行简化。将比较均衡、由强渐弱、先渐强后渐弱、由弱渐强的实际降雨过程进行线性简化，得到均布型、前峰型、中峰型、后峰型4种降雨模式[14]。以R表示小时降雨强度(mm/h)，t表示降雨历时(h)，模拟福州市某次强台风，降雨持续96 h，降雨总量192 mm，则上述4种降雨模式的数学模型分别为：均布型R=2 (0≤t≤96)；前锋型R=4-；中峰型(0≤t＜48)，；后峰型R=(0≤t≤96)。

2.2 花岗岩残积边坡模型

以福州市软件园某边坡为工程背景，该边坡高31 m，坡角33°，坡体自上而下分布花岗岩残积砂质粘土、散体状强风化花岗岩、碎裂状强风化花岗岩，地下水为岩层裂隙水，花岗岩残积土处于非饱和状态，为潜在滑坡体。取边坡顶宽 10 m、底宽50 m，建立边坡有限元模型，共划分546个节点，500个单元(图1)。图1中虚线为地下水位线，最高、最低水头分别为13 m、6 m，地下水位线以上左右边界设为自由流动面，坡顶坡面流量Q等于降雨强度R。边坡岩土层有关参数见表1。

表1 边坡岩土层参数Table 1 Parameters of the slope rock and soil

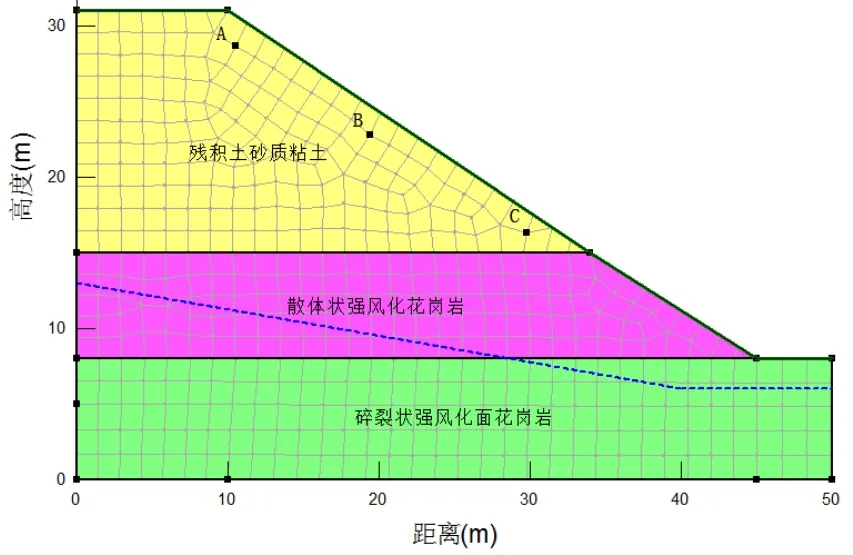
图1 边坡数值模型Fig.1 Numerical model of the slope

3 降雨入渗数值分析

3.1 孔隙水压力

根据模型边坡的地质构造，降雨可能引发的潜在滑动体是花岗岩残积砂质粘土层，故首先运用Geo-Studio软件seep模块自带的样本函数，取饱和渗透系数 2×10-6cm/s，初始饱和含水量 50%，得到花岗岩残积砂质粘土的土水特征曲线，见图 2。由图2可得到瞬态流控制方程所需的有关参数，选择降雨模式的边界条件，然后运行Geo-Studio软件的seep模块进行求解，得到边坡体在降雨过程中的孔隙水压力值。

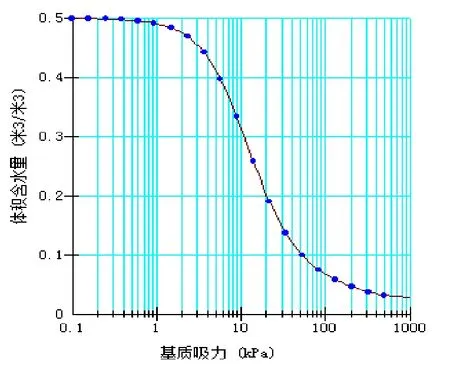
图2 残积砂质粘土的土水特征曲线Fig.2 Soil water characteristic curve of residual sandy clay

对模型边坡花岗岩残积砂质粘土层，在其上部、中部、下部各选取一点(图1中A、B、C三点)进行孔隙水压力分析。在4种降雨模型下，A、B、C三点的孔隙水压力的变化情况见图3。由图3可见：边坡的初始孔隙水压力分布不均匀，坡体上部(A 点)初始孔压最小，其次是中部(B点)，下部(C点)最大；降雨入渗后，坡体孔压的增幅也不均匀，其中A点孔压最大增幅约74 kPa，B点孔压最大增幅约64 kPa，C点孔压最大增幅仅11～12.5 kPa。可见，降雨入渗对边坡的中上部不利影响比较显著，而对坡体下部的不利影响相对较小。再比较4种不同降雨模式下边坡中上部A、B两点的孔压变化，不同降雨模式产生的最大孔压增幅是相同的，但历时差异较多，前峰型和均布型的变化历程基本相同，完成最大孔压增幅的历时最短，其中 A点约20 h，B点约30 h；中峰型其次，其中A点约36 h，B点约48 h；后峰型历时最长，其中A点约60 h，B点约72 h。这说明，若降雨诱发滑坡灾害发生，则前峰型和均布型降雨历时最短，其次是中峰型降雨，而后峰型降雨历时最长。

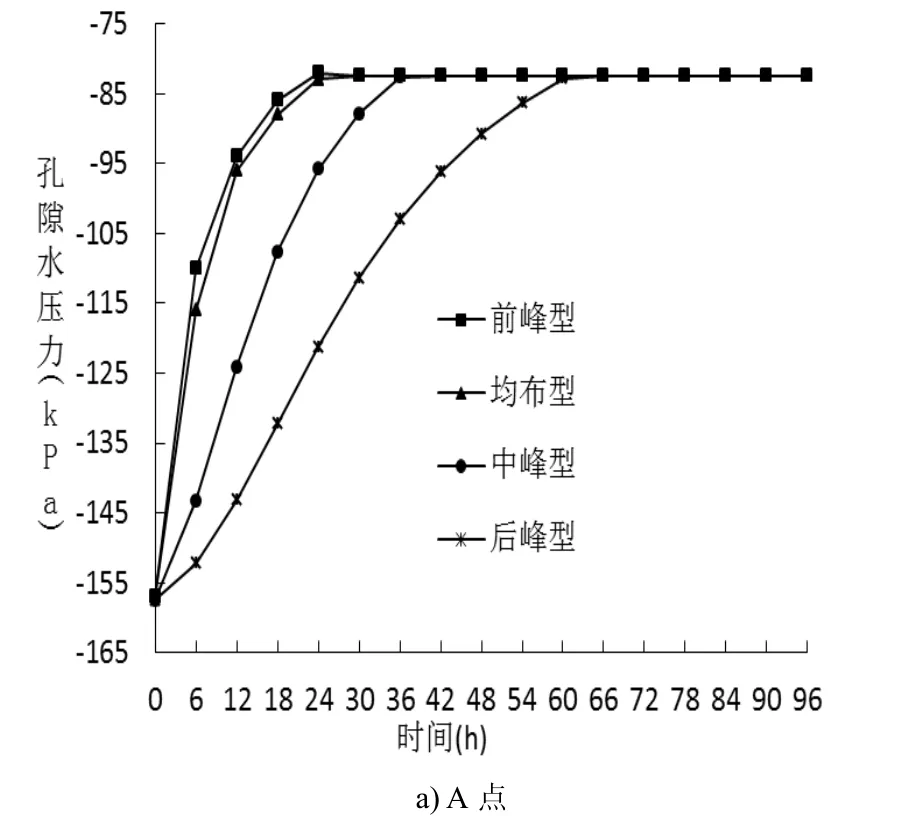
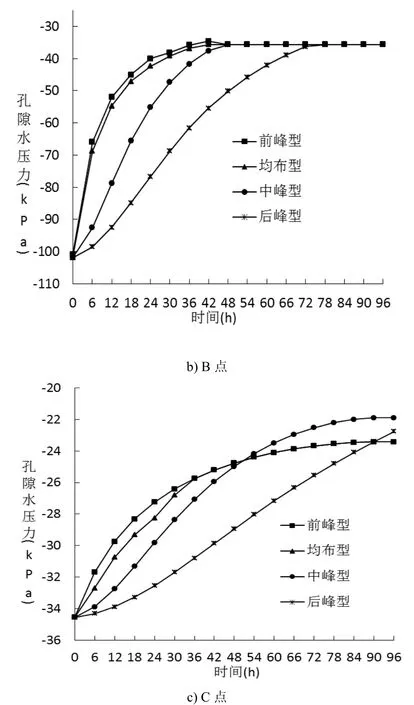
图3 孔隙水压力与降雨持时关系Fig.3 Relationship between pore water pressure and rainfall duration

3.2 边坡安全系数

本文的花岗残积土边坡是以福州市软件园某边坡为工程背景，规范GB 50330-2013《建筑边坡工程技术规范》表明对于土质边坡，可采用圆弧形滑面进行计算，对于圆弧形滑面这一规范建议采用简化Bishop法进行计算。因此按规范要求，采用简化 Bishop法对花岗岩残积土边坡进行稳定性分析计算。以seep模块为母模块，新建slope子模块，然后将图3孔隙水压力值导入Geo-Studio的slope模块中，选用Bishop法，在边坡上选择滑动面的出入范围，进行计算求解即可得到边坡的稳定安全系数Fs。在4种降雨模式下，模型边坡的安全系数随降雨持时的变化情况见图4。

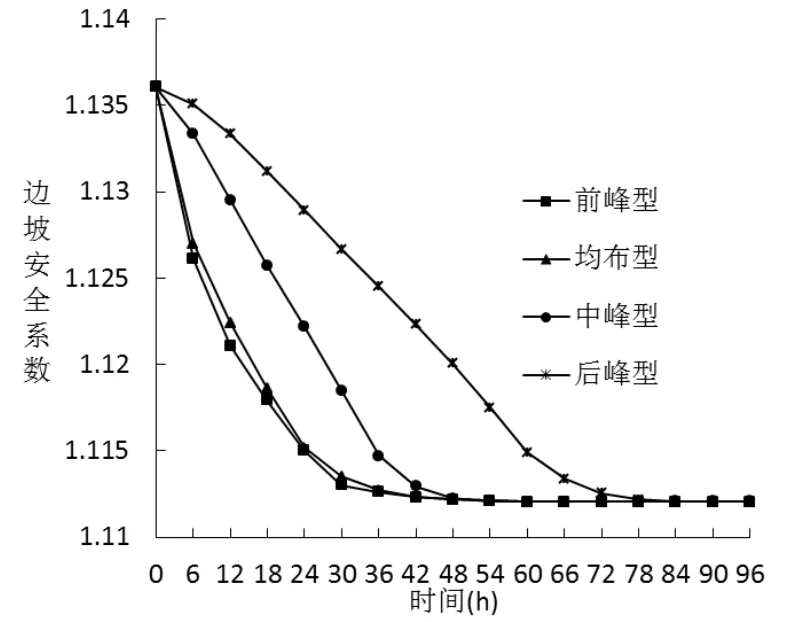
图4 边坡安全系数随降雨持时变化Fig.4 Variation of the slope safety factor with rainfall duration

由图4可见：随着降雨历时的延长，坡体孔压逐渐增大而基质吸力逐渐减小，边坡稳定安全系数随之减小；4种不同降雨模式的最大减幅是相同的，但历时不同。前峰型和均布型降雨，最大减幅的历时约30～36 h；中峰型降雨，最大减幅的历时约42～48 h；后峰型降雨，最大减幅的历时约 72～78 h。这一结果与上述坡体孔压增幅的变化规律是相吻合的，而且最大减幅历时与坡体中部(B点)的孔压最大增幅历时接近。