基于动态权重SA-PSO 的工艺路线决策

邓 伟，宋 景, 黄昊旻，姚固文

（贵阳学院机械工程学院，贵州，贵阳 550005）

1 概述

随着智能制造的兴起，计算机辅助工艺规划越来越引起企业的重视。工艺路线优化决策是工艺规划工程中的重要环节，其主要包括加工方法的排序及工艺方案的选择。工艺路线优化问题属于NP-hard问题，在工艺路线优化工程中，工艺路线不仅受到切削参数、加工方法、机床和刀具选择等的影响，还受到工艺优先约束关系的影响。传统的经典算法如SD法、Newton等由于算法本身的限制，已经很难求解这类问题，所以寻找高效的智能算法求解该问题成为了国内外学者的研究重点，也取得了丰硕的研究成果[1-3]。

粒子群算法[4]（Particle swarm sptimization,PSO）源于复杂适应系统（Complex Adaptive System,CAS），最早是在 1995年由 Eberhart和Kennedy提出，国内外学者对PSO算法进行了大量的研究[5-8]。PSO算法由于其容易实现的特点，取得了大量的实际应用，但它和其它随机优化算法一样，也存在早熟收敛现象，极易陷入局部收敛。在粒子群优化算法中，算法的收敛速度和精度是相互矛盾的，在算法初期，希望算法拥有较大的搜索步长，快速收敛到最优解附近，但较大的搜索步长同时也意味着算法后期不易收敛，还可能从全局最优区域中跳出。在粒子群算法中，动态权重对算法搜索精度有着很大的影响，文献[9-12]均对算法中的权重系数进行了研究，取得了良好的效果。

本文在已有研究的基础上，使算法中的权重系数根据当前粒子到全局最优粒子的距离而动态递增，同时为了避免算法过早陷入局部最优，在标准粒子群算法中引入模拟退火思想，使每个粒子的速度和位置更新过程中加入模拟退火机制，使粒子群按Metropolis准则接受优化解的同时概率接受恶化解，有效避免局部收敛。最后建立了以加工成本为优化目标的目标函数，结合实际的工艺约束，详细介绍了该算法进行加工工序决策及相关机床和刀具的选择过程。

2 工艺排序约束矩阵

机加工过程中为了避免加工操作间发生干涉以及保证加工质量，零件上的几何特征在加工过程中必须满足一定的先后顺序，使各加工操作之间产生先后约束。这类约束主要来源于工艺制定过程，为确保工艺路线的合理性，必须遵循这些约束。在机加工过程中，这些约束应遵循以下规则：

1）先主后次。在制定机加工工艺时，应先加工主要表面，后加工次要表面；

2）先面后孔。当一个待加工面上存在孔系特征时，该面的加工操作须安排在孔系特征加工操作之前；

3）先粗后精。同一个特征的若干加工操作须满足粗加工——半精加工——精加工——光整加工这样的加工次序；

4）基准优先。基准面应首先加工，如果存在多个基准面，则需要按照基准面的转换顺序来决定基准面的加工顺序。

2.1 操作优先图

在满足约束规则的条件下，零件特征的加工先后关系一般采用一个有向图将其形象地表示出来，称为操作优先图。如图1所示，图中的圆圈称为节点，每一个圆圈均表示一个操作，圆圈里的数字表示该操作的编号（每个编号唯一且不重复），圆圈和圆圈之间的有向线表示操作的先后顺序。当两个圆圈之间通过有向线直接连接时，表示这两个操作有严格的优先关系。如图1中，操作1和操作3就存在严格的优先关系。

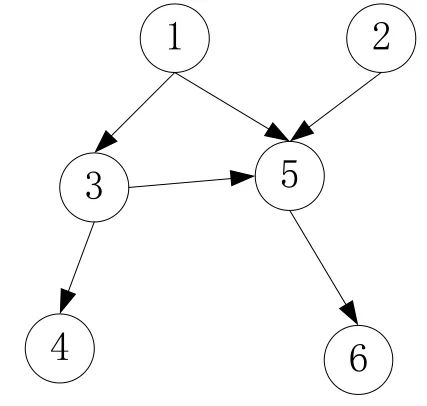
图1 操作优先图Fig.1 Operation precedence graph

操作优先图能直观地描述出各个加工操作之间的先后顺序。为了便于计算机识别推理，需将操作优先图转化为计算机可以识别的优先关系矩阵，也叫约束矩阵。若某个工件上的所有特征需要n个加工操作，则优先关系矩阵可表示为，式中的值为0或1。这里作如下定义，若第i个操作先于第j个操作，且存在严格的优先关系时，则=1，否则= 0 ，显然矩阵P为n阶0-1矩阵。按照此转化规则，图1所示的操作优先图可转化为图2所示0-1矩阵。

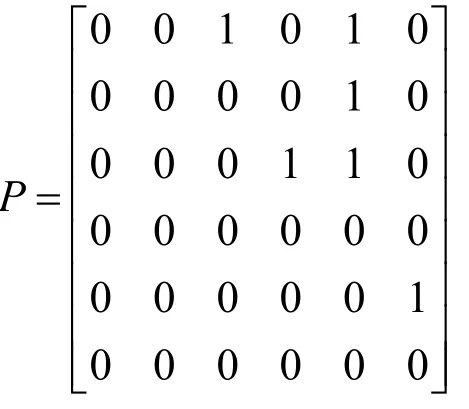
图2 约束矩阵Fig.2 Constraint matrix

2.2 操作优先图拓扑排序

按照操作优先图给出的操作先后关系，将操作优先图中所有圆圈排成一个线性序列，使得该图中所有应存在的前驱和后继关系都能得到满足，由此所得到的线性序列称之为拓扑有序序列。拓扑排序步骤如下：

1）输入操作优先图；

2）在图中任选一个没有直接前驱的节点，并输出；

3）从优先图中删去该节点，同时删除该节点发出的有向边；

4）重复步骤2）、3），直到全部节点均已输出，拓扑有序序列形成，拓扑排序完成。

若操作优先图中还有节点未输出，但此时已跳出排序循环，说明优先图中必定存在有向环，此时操作优先图所代表的操作流程将无法进行。文献[13]对有向环检测做了详细的算法说明。

各个操作的入度值按式（1）进行计算：

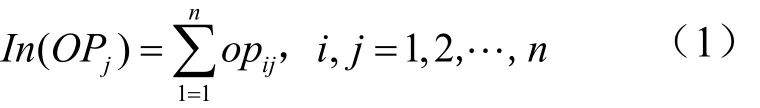
其中，为约束矩阵中第i行j列的元素值。由此可知，第1步操作的入度值为0。对于删除入度值为零的顶点，则可以以弧头顶点的入度值减 1来实现。

3 动态权重SA-PSO算法

3.1 标准粒子群算法

假设一个由N个粒子组成的群体对D维空间进行搜索，任意一个粒子的位置可表示为()，对应的速度可表示为)，任意一粒子的历史最优值记作=)，整个群体的历史最优值记作= ()。在每一次迭代过程中，群体里的每个粒子同时跟踪自己的历史最优值与群体历史最优值来更新自己的位置和速度，当迭代终止时，将当前的群体最优值作为所求问题的最优解。单个粒子速度和位置的更新规则如式（2）、（3）所示。

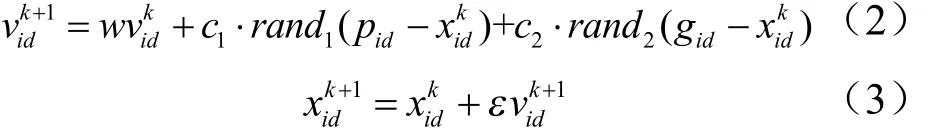
式（2）中，k代表迭代次数；w为惯性权重，是保持原来速度的系数，表示上一次迭代的粒子速度对当前迭代粒子速度的影响，影响算法全局寻优能力和局部寻优能力；为学习因子，分别代表粒子对自身历史最优值的学习程度和对群体历史最优值的学习程度；和是为保持群体多样性而设置的[0,1]之间的随机数；ε为速度约束因子。

3.2 动态权重SA-PSO算法

在优化求解过程中，最终的目的是寻找全局最优解。对于算法的每次迭代，都应重点考虑在全局最优粒子领域内进行搜索，因为在此领域内有可能存在真正的全局最优解。从式（2）可知，惯性权重决定着粒子的飞行速度，由于算法开始时随机产生的粒子几乎不可能在最优位置，此时较大的惯性权重w意味着较大的搜索步长，有利于算法快速收敛到局部或全局最优点附近，但随着迭代次数的增加，有，，则式（2）近似为， 可知此时惯性权重对粒子飞行速度有着决定性的影响，如此时惯性权重w依旧很大，当前粒子有可能跳出全局最优的领域范围。因此较为理想的方法是惯性权重w随着当前粒子与全局最优粒子的距离而变化。当距离远时，较大的惯性权重w有利于粒子的大范围搜索；当距离近时，较小的惯性权重w可保证其收敛精度。

用li表示第i个粒子到全局最优粒子的距离，并限定粒子到全局最优粒子的距离最大为，最小为。当距离大于最大值时，惯性权重取最大值；当距离小于最小值时，权重取最小值；当距离在两者之间时，惯性权重应随着距离递增。其计算公式如下：

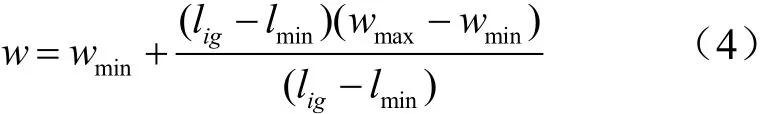
为了使适应度较好的个体尽可能地保留，同时也为了避免算法局部收敛，将模拟退火思想引入PSO算法当中。模拟退火算法[14]（Simulated Annealing Algorithm,SA）源于金属退火原理，利用物理退火与优化问题的相似性，将优化目标看作是退火过程中的金属能量状态，并利用Metropolis准则接受优化解和概率接受恶化解，从而实现大范围粗略搜索与局部精准搜索的有效结合。动态权重SA-PSO算法过程如下：

1）初始化搜索空间维度D，设置最大迭代次数K并产生一个有N个粒子的种群；

2）初始化惯性权重w，学习因子，退火起始温度T0，终止温度T；

3）计算第k次迭代中每个粒子的适应度，i= 1 ,2,… ,N；

4）将粒子的适应度与个体历史最优值进行比较，若优于，则用替代，否则保持不变；

5）将每个粒子的适应度与群体最优进行比较，若优于，则用替代，否则保持不变；

6）增加迭代次数，若，则进行步骤7）。否则，结束计算；

7）根据式（5）改变惯性权重；

8）根据式（1）、（2）更新每个粒子的的位置和速度；

9）计算更新后的每个粒子适应度；

10）计算，按模拟退火接受概率) = min{ 1,exp接受或舍弃更新后的位置，由文献[2]可知，a为温度衰减率，通常取为；若，则接受新位置为当前位置，并返回步骤4）；若，则产生一个[0,1]之间的随机数ε；若 e xp，则接受新位置，返回步骤4），否则不接受位置更新，返回步骤7）。

4 工艺路线优化目标函数的构建

工艺路线优化是将约束作用到加工操作上，在一定的约束条件下获得最优的加工工艺方案，使加工时间、加工成本等目标达到最优。工艺路线优化过程中，常用的评价指标有加工时间（T）和加工成本（C）。本文将最小加工成本作为优化目标进行工艺线路优化，加工成本包括机床成本（MC）、刀具成本（TC）、机床变换成本（MCC）、装夹变化成本（SCC）和刀具变换成本（TCC），计算方式如式（5）～（9）所示[15]。

式（5）～（9）中，MCI为机床成本指数，表示机床在机加工过程中的单位时间成本；TCI为刀具成本指数，表示机加工过程中所用刀具的单位时间成本；MCCI为机加工过程中机床变换成本指数，表示机加工过程中每变换一次机床所需要的成本，包括人工成本、搬运成本、运输成本等；SCCI为工艺线路中的装夹变换成本指数，表示机加工过程中每更换一次装夹方式所需要的成本；TCCI为刀具变换成本指数，表示机加工过程中每更换一次刀具所需要的成本；ti表示第i工步所消耗的机加工时间，分别表示第i工步所采用的机床、夹具及刀具。

综上，零件加工过程中的总成本为式（10）所示。

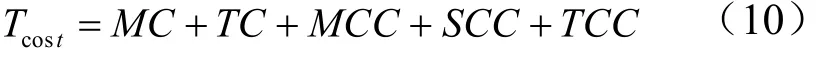
5 实例验证

5.1 实例描述

如图3所示零件，通过分析得到该零件一共有9个特征需要加工，共需要11个加工操作，每个特征的机加工时间可根据切削参数进行计算。

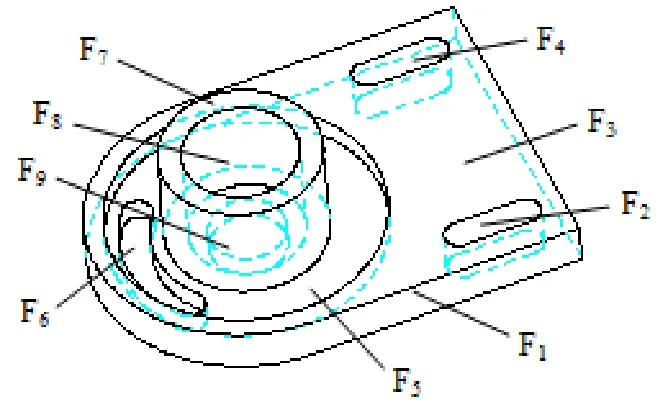
图3 零件模型Fig.3 The part model

零件加工信息如表1所示。

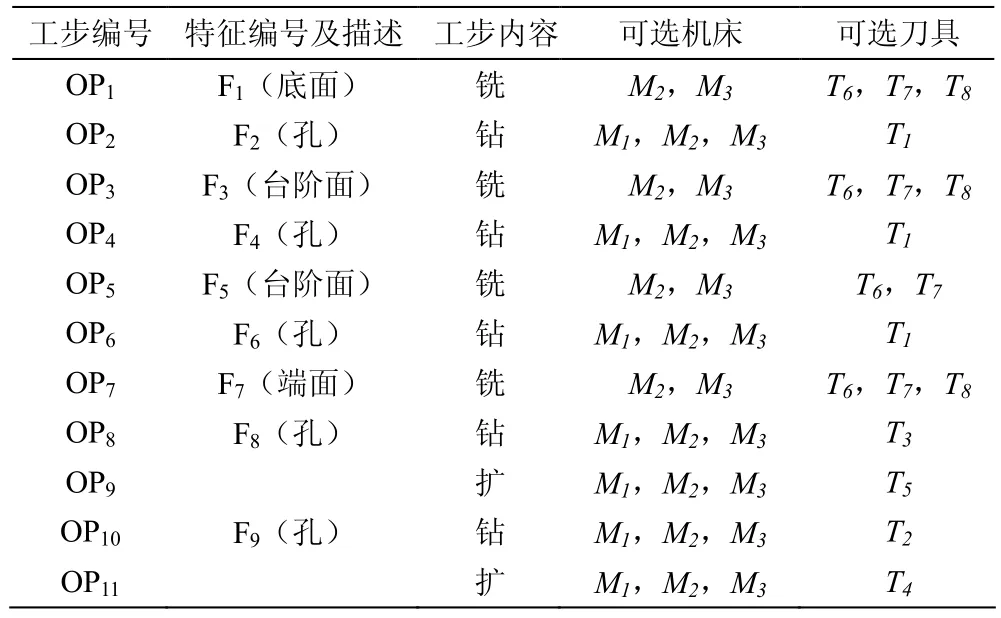
表1 零件加工信息Table 1 Processing information of the part

上述11个工步的操作优先顺序图如图4所示，按照文中所述规则，可将该操作优先图转化为约束矩阵。

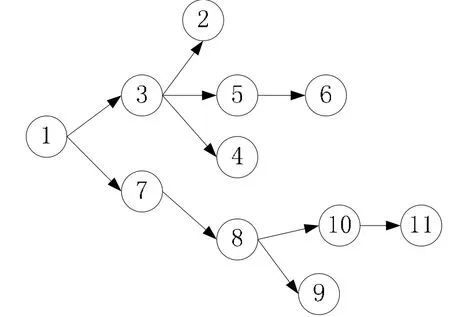
图4 操作顺序图Fig.4 Operation sequence graph

在该零件加工过程中，共有钻床、三轴立式铣床、数控立式铣床三种机床可供使用，其机床成本指数MCI分别为3、5、8，机床变换成本指数MCCI=5，装夹变换成本指数SCCI=3，刀具变换成本指数TCCI=1。可用刀具信息如表2所示。

表2 刀具信息Table 2 Tool information

5.2 工序的确定

根据文中所述算法，初始化粒子群粒子数N= 40，设置最大迭代次数K= 100，位置更新时速度约束因子ε=1，退火起始温度，终止温度，温度衰减率α=0.8，=1，，惯性权重= 0 .9，= 0 .2。在迭代运算中，设每次换刀时间均为 5 s，装夹时间为15 s，并将换刀时间和装夹时间计算在机床使用成本时间以内，如特征F1切削时间为90 s，则加工该特征的机床的使用时间记为110 s。为了验证本文算法的有效性，应用标准粒子群算法对图3进行了工艺路线求解，初始条件与文中算法一致。两种算法的迭代对比如图5所示。

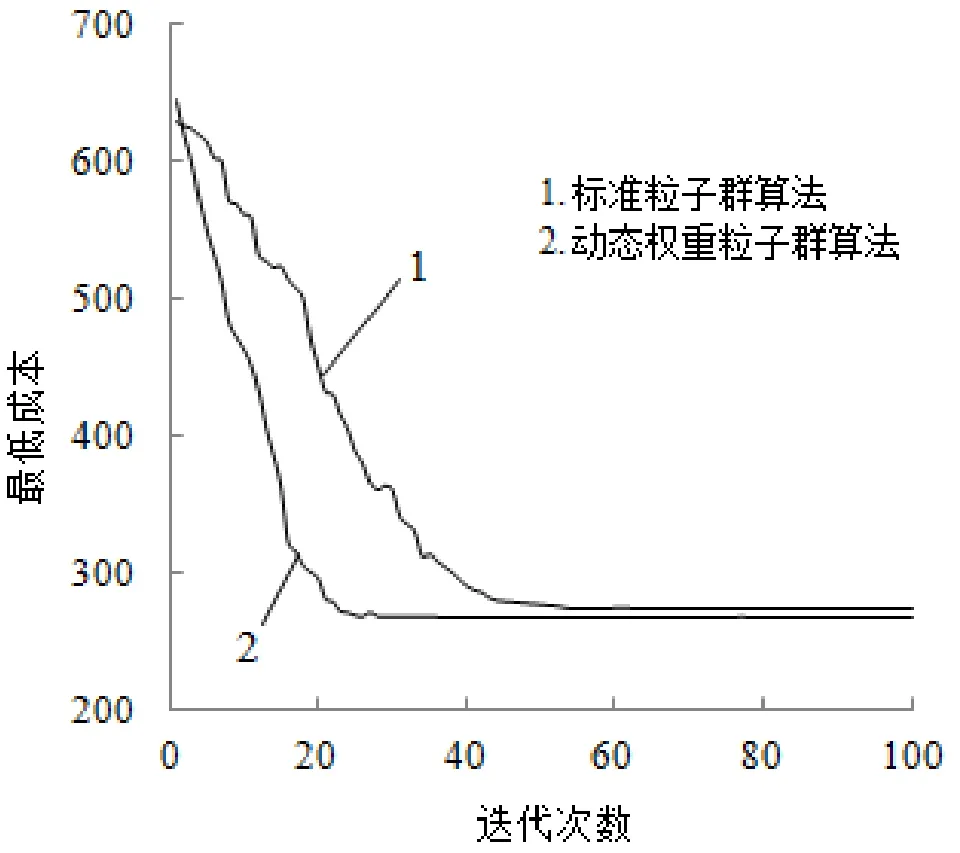
图5 两种算法运算结果Fig.5 The results of two algorithms

由运算结果可知，采用标准粒子群算法时，迭代次数为54时收敛到最优值272.3。采用文中的算法时，迭代次数为29时收敛到最优值266.7。可知采用文中算法时收敛速度相对较快，目标函数值更优，得到较优机加工顺序为：

OP1——OP3——OP7——OP5——OP2——OP4——OP6——OP8——OP10——OP11——OP9。

详细机床和刀具的选择如表3所示。

表3 最优工艺路线Table 3 Optimal processing route

6 结束语

在满足实际工艺约束的情况下，解决复杂的机加工排序一直是工艺规划过程中的难点之一。本文在标准PSO算法基础上，引入了模拟退火精英保留策略，并使权重随着当前粒子到最优粒子的距离变化而改变，一定程度上加快了算法早期的收敛，提高了算法后期收敛精度。最后以某零件的加工为例，以最小生产成本为优化目标，得出了较为理想的机加工工序，表明文中所建立的算法在工艺路线决策中具有一定的应用价值。

[1]Triki H, Mellouli A, Masmoudi F. A multi-objective genetic algorithm for assembly line resource assignment and balancing problem of type 2 (ALRABP-2)[J]. Journal of Intelligent Manufacturing, 2017, 28(2):371-385.

[2]张思建,方彦军,贺瑶,等. 基于模拟退火算法的 AVS/RS多批货箱入库货位优化[J].武汉大学学报:工学版, 2016,49(2):315-320.

[3]Cinar D, Oliveira J A, Topcu Y I, et al. A priority-based genetic algorithm for a flexible job shop scheduling problem[J]. Journal of Industrial & Management Optimization, 2017, 12(4):1391-1415.

[4]张水平,王碧. 动态搜索空间的粒子群算法[J].计算机应用研究, 2016, 33(7):2047-2050.

[5]Garg H. A hybrid PSO-GA algorithm for constrained optimization problems[J]. Applied Mathematics &Computation, 2016, 274(11):292-305.

[6]Aziz M A A, Taib M N, Hussin N M. An improved event selection technique in a modified PSO algorithm to solve class scheduling problems[C]. Industrial Electronics &Applications, IEEE, 2016:203-208.

[7]毛君,杨辛未,潘德文,等. 基于改进粒子群算法的刨煤机多目标优化设计[J].机械设计与研究, 2016(1): 168-170.

[8]徐立云,徐昌飞,邓伟,等. 基于SA-PSO算法的发动机缸体机加工线平衡研究[J].农业机械学报, 2014, 45(2):16-21.

[9]谭熠峰,孙婷婷,徐新民. 基于动态因子和共享适应度的改进粒子群算法[J]. 浙江大学学报:理学版,2016,43(06):696-700.

[10]封京梅,刘三阳. 基于惯性权重指数递减的粒子群优化算法求解绝对值方程[J]. 吉林大学学报:理学版,2016,54(06):1265-1269.

[11]张志宇,白云霞. 粒子群算法不同惯性权重之间的比较[J].淮海工学院学报:自然科学版, 2016,25(01):1-6.

[12]皮倩瑛,叶洪涛. 一种动态调节惯性权重的粒子群算法[J].广西科技大学学报,2016,27(03):26-32.

[13]李爱平,鲁力,王世海,等. 复杂箱体零件柔性机加工生产线平衡优化[J].同济大学学报:自然科学版, 2015,43(4):625-632.

[14]杨卫波,王万良,张景玲,等. 基于遗传模拟退火算法的矩形件优化排样[J].计算机工程与应用, 2016,52(7):259-263.

[15]黄伟军,蔡力钢,胡于进,等. 基于遗传算法与有向图拓扑排序的工艺路线优化[J].计算机集成制造系统, 2009,15(9):1770-1778.