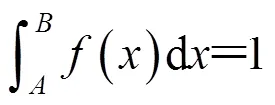应急演练中基于G-R关系的主余型地震余震震级模拟1
2018-06-01王青平王辉山林岩钊周施文张树君
王青平 王辉山 肖 健 林岩钊 周施文 张树君
应急演练中基于G-R关系的主余型地震余震震级模拟1
王青平 王辉山 肖 健 林岩钊 周施文 张树君
(福建省地震局,福州 350003)
在现有的日常地震演练过程中,与应急救援密切相关的地震余震信息产品较为缺乏,直接影响发震构造的判断以及影响场修正等关键环节。本文从计算机系统提供的均匀分布随机数出发,运用反函数法模拟生成余震序列,并进行系统检验,证实该方法产生的余震序列满足G-R频次关系。模拟生成的余震震级数据既有助于增强地震应急救援演练的现实性,也有助于丰富地震应急宣传产品,提升地震部门的履职能力。
地震序列 G-R关系 余震震级模拟 反函数法 随机数
引言
地震序列是在某一时间段内连续发生在同一震源体内的一组按次序排列的地震。主震是地震序列中最大的地震,前震是序列中主震前所有地震的统称,余震是序列中主震后所有地震的统称(中华人民共和国国家质量监督检验检疫总局等,2005)。
周蕙兰等(1982)利用主震所释放能量占全序列所释放总能量的比例E对地震序列进行划分:当E≥99.99%为孤立型(IET,Isolated Earthquake Type),其主要特点是几乎没有前震,也几乎没有余震;当90%≤E<99.99%为主余型(MAT,Mainshock-Aftershock Type),其主要特点是主震震级突出,主震和最大前震、最大余震的震级相差显著。当E<90%为震群型或双震型地震(MMT,Multiple MainshockType),其主要特点是没有突出的主震,主要能量是通过多次震级相近的地震释放出来的。蒋海昆等(2006)统计1970年以来中国大陆记录相对完整的294次5.0级以上地震序列,孤立型、主余型以及多震型的比例分别占23%、59%和18%。
在余震强度分布特征方面,Gutenberg等(1944)在研究世界地震活动时,根据全球各大地震区6级以上地震数目的统计发现地震的震级与频度存在以下关系:lg=-,它反映了地震序列中大小地震的比例关系及其变化,亦称G-R关系式,式中值和值分别反映地震活动水平和强度分布特征(吴开统等,1990);Bath(1965)提出,主震震级与最大余震的震级之差平均为1.2,史称“巴特定律”;马宏生等(2005)根据G-R关系以及能量-震级经验关系,推导出一个相对独立的应变积累速率公式;蒋海昆等(2006)对1970年以来记录相对完整的294次5.0级以上地震序列资料进行研究,余震序列1年内最大余震震级与主震震级正相关。傅征祥等(2008)对1966—1999年中国大陆浅源主震型序列余震的值进行分析,88个震例样本的值平均值为0.73。
在余震序列模拟方面,Eob等(1992)基于稳态泊松和马尔科夫过程的统计模型,以余震释放的总能量作为控制余震序列的长度,利用蒙特卡罗(Monte-Carlo)方法对地震序列的时间间隔和震级大小进行协同模拟。整个过程较为复杂,同时并未对模拟的序列进行回归分析验证模拟系统。刘善琪等(2013)在假定地震的发生与时间的关系遵循稳态泊松模型,采用人工生成值为常数的地震目录,并用蒙特卡罗方法对值进行统计分析,研究结果显示影响值计算误差的主要因素为样本数量、震级间隔以及震级误差。
对余震序列的研究是理解地震过程的重要途径。国内外学者对余震的研究一般是基于完整的地震序列来总结余震的类型和主余震之间的统计特征。任雪梅等(2009)根据主震震级与余震震级、时间间隔与震中距之间的经验关系和统计规律进行探索,结果表明对某些主震后的强余震具有一定的参考价值。王伟锞等(2011)提出余震法来快速判定宏观震中,结果表明利用余震法可在震后6小时根据地震破裂性质推断宏观震中,其准确度、时效性都能为震后快速评估提供较为可靠的依据。
依托国家地震社会服务工程项目的建设,福建省地震局的地震应急服务水平得到较大的提升,而在现有的日常演练过程中缺少与应急救援密切相关的地震余震信息产品。本文以实际需求为导向,基于常用的计算机高级程序设计语言提供的连续均匀分布的独立伪随机数,运用反函数法模拟生成满足G-R频次关系的余震震级分布。根据主震震级自动产生的余震序列,为日常地震演练提供可靠的余震震级模拟数据,以丰富宣传产品种类,提升服务水平质量。
1 随机数的基本理论
1.1 随机数
真正意义上的随机数(Random number)在某次产生过程中是按照实验过程中表现的分布概率随机产生的,其结果是不可预测的。计算机随机函数产生的“随机数”并不随机,是伪随机数(Pseudo-random number),产生的伪随机数序列并不是相互独立的,每个数均依赖于前一个数,但只要这种相关性弱到一定程度就可以认为是相互独立的,产生的序列是“随机”的。好的随机数产生器至少要满足以下3个要求:
(1)周期性大:随机数序列并非是永不重复的,经过一个很长的周期后,序列形成一个循环重复;
(2)随机性好:即随机数序列中所有随机数之间没有大的关联,或自相关系数很小;
(3)算法简单:为了得到好的统计结果,通常需要较大的样本空间,随机数产生器的速度也是一个非常重要的考虑因素。
1.2 均匀随机数
均匀随机数就是在某个区间内任何一点出现的概率是相等的,没有规律可循,它是产生其它概率分布的随机数的基础和关键(王菊等,2015)。目前使用最多、最广的均匀随机数生成器是基于Lehmer在1951年首先提出的线性同余随机数生成器(Linear Congruence random number generator)。基本方法如下:
对于任意初始整数0,随机数序列由如下递推公式确定:
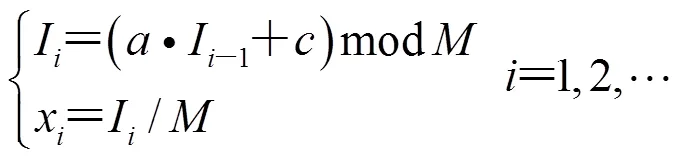
其中是模数(modulus),>0;初始值0也称种子(Seed),0≤0<;是乘子(multiplier),0<<;是增量(additive constant),0≤<;mod是取模运算。x为均匀伪随机数,0≤x<1。通常用表达式LCG(,,,0)表示上述随机数生成器。考虑到随机数的产生效率,模数通常取2的整数次方(在32位计算机上,可取231),取模操作可以用位移操作来代替,提高运算速度。
通过(1)式可以得到[0,1]区间内的均匀随机数,通过下列的线性变换可得到[,]区间内的均匀随机数:

1.3 任意概率分布随机数
对于[,]区间内的均匀分布随机数,其归一化条件可以表示为:
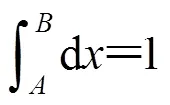
任意分布()的随机数的归一化条件可以表示为: