强震动记录的低频截止频率自动搜索算法1

于海英 徐 旋 张同宇



强震动记录的低频截止频率自动搜索算法1

于海英1，2）徐 旋1，2）张同宇1，2）

1）中国地震局工程力学研究所，哈尔滨 150080 2）中国地震局地震工程与工程振动重点实验室，哈尔滨 150080

本文针对传统方法在强震动记录处理中确定滤波低频截止频率效率较低的问题，提出一种确定滤波低频截止频率的自动搜索模型，并利用统计学习方法中的损失函数确定自动搜索模型流程的结束条件。基于2008年汶川和2013年芦山两次地震主震和余震获得的强震动记录，将自动搜索算法得出的结果与传统方法确定的低频截止频率进行比较，分析自动搜索算法产生误差的原因，进而提出自动搜索算法应遵循的原则和适用条件。结果表明该算法计算效率比传统方法有很大提升，特别适合海量强震动记录的批量处理。

强震动记录 滤波 低频截止频率 自动搜索模型 损失函数

引言

强震动记录处理是地震工程与工程地震相关研究的基础工作，可以为抗震设防、地震烈度速报和预警以及重要工程强震动观测等工作提供高质量的科学数据。然而，受环境振动干扰等因素影响，强震动记录不可避免地隐含噪声。因此，研究如何对强震动记录中的噪声进行识别尤为重要。而无论是过去还是将来，频率域去噪都是一项主要的去噪技术（张军华等，2006），所以滤波技术的研究在强震动记录处理中占有非常重要的位置。

滤波器的选择是强震动记录处理中的核心问题之一。不同强震动记录处理机构选择的滤波器有所不同。USGS采用双向巴特沃斯非因果滤波器；CSMIP使用Ormsby或低通巴特沃斯滤波器进行非因果滤波；COSMOS采用因果与非因果结合的多种滤波器类型。根据张同宇（2016）的研究，对于强震动记录事件分析推荐使用巴特沃斯（IIR）非因果滤波，对于强震动记录实时处理推荐使用巴特沃斯（IIR）因果滤波，在分析芦山地震强震动记录时推荐使用4阶巴特沃斯（IIR）滤波。本文采用双向巴特沃斯非因果滤波器，滤波阶数为4阶。

对于数字强震动记录，滤波通带的高通低频截止频率和低通高频截止频率一直是滤波器中的重要参数。根据奈奎斯特采样定理，强震动记录的高频截止频率最大值不得大于采样频率的二分之一，低频截止频率的最小值（低频截止频率的下限）不得小于记录时间长度倒数的2倍。CSMIP一般选23Hz作为高频滤波的截止频率，25Hz作为终止频率，选0.05—0.07Hz作为低频滤波的截止频率。Syun'itiro等（1988）根据拟速度谱（阻尼比为5%）在长周期段的特点来确定截止频率。Kenzo等（1988）研究了SMAC强震仪所获得的强震记录，截止频率由1/谱确定。根据谢礼立等（1983）和周宝峰（2012）的研究，高频截止频率对于强震动记录位移时程基线偏移的影响很小，考虑到抗震结构设计中比较感兴趣的频带范围，本文高频截止频率取35Hz。

低频截止频率对于强震动记录位移时程基线偏移的影响很大。而目前已有的低频截止频率确定方法，如经验法、拟速度谱法、震源谱理论法、傅里叶幅值谱法等，都不能够有效且准确地滤除低频噪声。比较好的方法是通过滤波后积分速度和位移的效果来判定选择的低频截止频率的合理性和准确性，也就是传统方法，但是这种方法的效率很低，不适用于我国强震动台网海量强震动记录的处理。本文针对传统方法的不足，开展自动搜索算法的研究，以满足目前海量强震动记录处理的需要，并把传统方法获得的结果作为自动搜索算法准确性的参考标准。

1 基础数据

本文选择的强震动记录为2008年汶川和2013年芦山两次地震主震和余震获得的强震动加速度记录。在这两次地震中，国家强震动台网获得了大批完整的强震动记录。从汶川和芦山地震加速度记录中筛选出符合条件的作为研究的基础，筛选的条件如下：

（1）三通道加速度峰值都大于等于20cm/s2。

（2）避免选取具有奇异波形特征（周宝峰等，2014a；Zhou等，2014b）的强震动记录。

由此，可以从汶川地震数据（中国地震局震害防御司，2008；于海英等，2009a）和芦山地震数据（国家强震动台网中心，2014；于海英等，2014）中，挑选符合条件的主余震强震动加速度记录共609条。所选强震动记录震级和强震动记录数目的关系如图1所示。

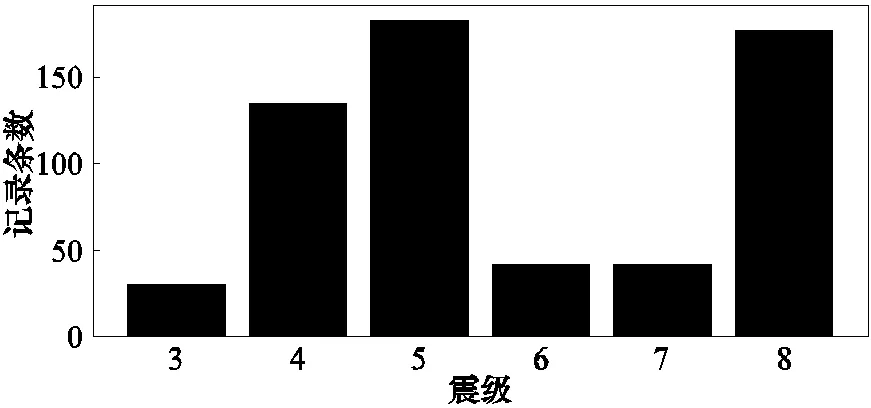
图1 各震级的强震动数目

2 低频截止频率自动搜索算法

2.1 算法原理与模型

传统方法通过观察强震动记录滤波后的位移时程来确定低频截止频率。在台站不发生永久位移的情况下，合理滤波后的位移时程末尾段均值接近于零并且末尾段拟合直线保持水平状态。类比传统方法提出确定低频截止频率的自动搜索算法模型如下：

（1）设置一系列频率点存储于一维数组LPS中，并将LPS按照升序进行排列，作为低频截止频率搜索的范围。频率点取的越密集，计算结果越精确，但是将增加数据的计算量。

（2）依次从LPS中取出一个低频截止频率进行滤波。因为LPS中的频率点已经升序排列，所以可以尽可能保留强震动记录的低频信息。

（3）根据滤波后的加速度时程计算位移时程。

（4）判断位移时程末尾段均值是否小于该位移时程峰值（PGD）的1/1并且位移时程末尾段斜率的绝对值小于对应位移峰值的1/2。若不满足条件，跳转至（2）；若满足条件，即确定低频截止频率。本文1和2为正数，根据传统方法的经验，1的范围为1—5，每间隔1取5个测试点；2的范围为50—800，每间隔10取1个测试点。

（5）将第4步确定的频率与根据奈奎斯特采样定理确定的低频截止频率的下限进行比较，取较大值作为低频截止频率。

算法模型流程图如图2所示。

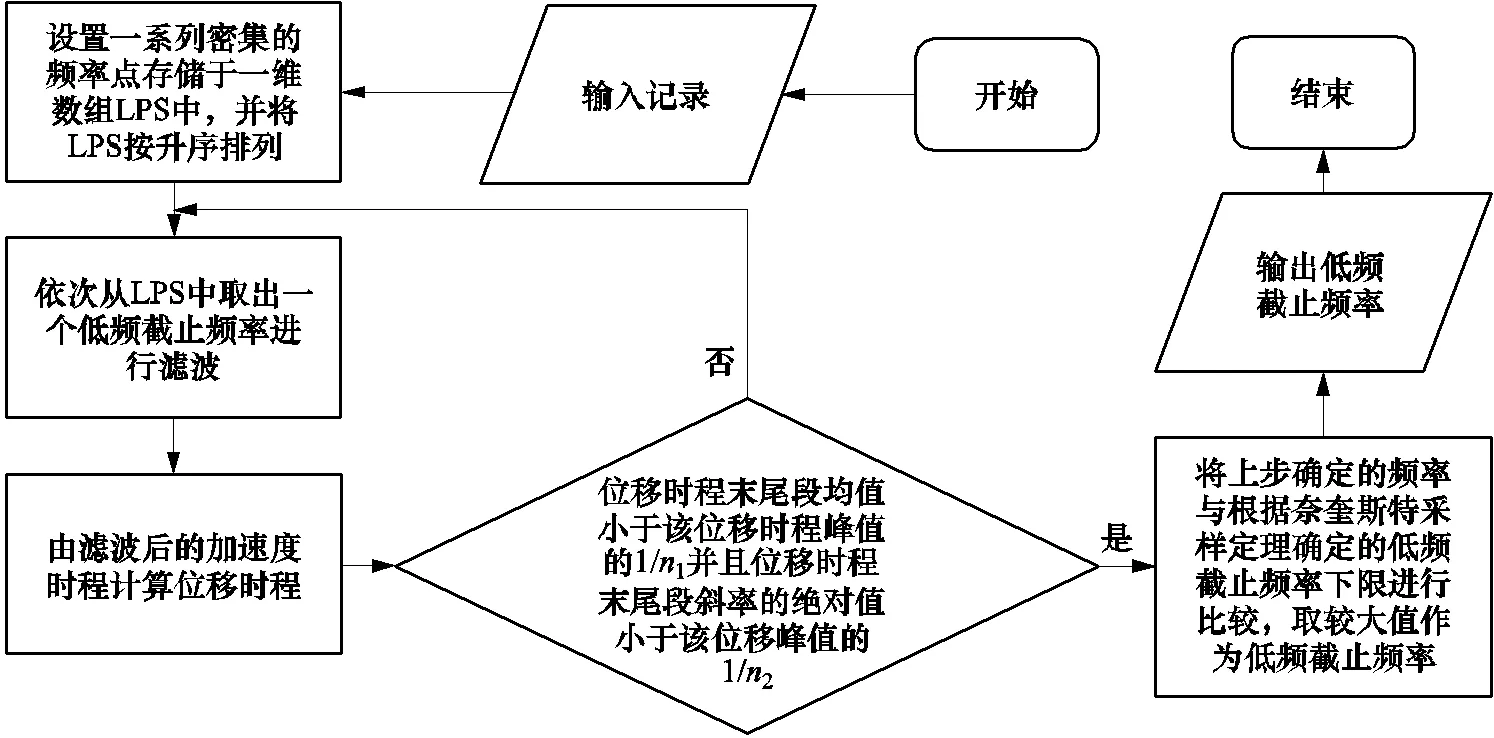
图2 自动搜索算法模型流程图

2.2 参数确定

在已有理论和研究的基础上，先对自动搜索模型中涉及到的相关参数做出如下约定：

（1）从0.04—1Hz之间间隔0.01Hz抽取97个频率点作为低频截止频率的搜索范围。

（2）采用双向巴特沃斯非因果滤波器，滤波阶数为4阶。

（3）滤波器的高频截止频率为35Hz。

（4）位移时程末尾段定义为强震动记录末尾占记录总长度四分之一的部分。

影响传统方法获取滤波低频截止频率的主要因素是对强震动记录位移时程情况的主观判断，因此自动搜索模型流程的结束条件是影响自动搜索算法精度的主要因素。从算法模型流程图（图2）中可知，确定算法模型流程的结束条件是确定1和2两个重要参数的值。在确定1和2之前，根据统计学习方法（李航，2012）中的思想，作如下说明：

（1）参与统计的所有强震动记录存储于X中。

（2）将自动搜索算法模型称为决策函数fn(X)，其中n＝(1，2)T，T表示转置。决策函数fn(X)表示利用n计算每一个强震动记录的低频截止频率，即自动搜索算法模型。

（3）根据传统方法确定强震动记录的低频截止频率存储于Y中。

（4）X、fn(X)和Y为列向量。

作出如上说明后，需要制定判断n优劣的准则，这样自然地引入损失函数来度量算法预测的好坏。损失函数是fn(X)和Y的非负实值函数，记作(Y，fn(X))。损失函数的种类比较多，本文采用的损失函数为：

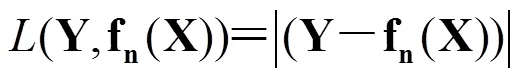
损失函数L(Y，fn(X))越小，决策函数fn(X)所采用的参数n就越好。根据传统方法的经验，自动搜索算法模型在n1、n2的取值范围进行搜索测试点。所有测试点计算出的损失函数如图3所示。其中n1＝4和n2＝440时，损失函数L(Y，fn(X))＝0.58为最小值。因此自动搜索算法的结束条件为：位移时程末尾段均值小于对应位移峰值的1/4并且末尾段线性回归斜率的绝对值小于对应位移峰值的1/440。

2.3 实际震例的应用

本文以传统方法确定的低频截止频率为参考标准，基于汶川和芦山两次地震主震和余震获得的609条强震动加速度记录，利用自动搜索算法计算低频截止频率。传统方法和自动搜索算法的结果如图4所示。

图4 传统方法和自动搜索算法的结果

以记录051YAL130420113402为例，依据自动搜索算法确定低频截止频率。该记录的时程长度为80.625s，根据奈奎斯特采样定理，该记录的低频截止频率下限为0.025Hz。该记录滤波后加速度时程、滤波后位移时程、PGD统计曲线（图中fPGD是不同频率滤波后的PGD，rPGD是未滤波的PGD）、位移时程末尾段均值统计曲线以及末尾段线性回归斜率的统计曲线如图5所示。

根据传统方法，利用不同的低频截止频率绘制滤波后速度时程、位移时程如图6所示。由图6可知低频截止频率对速度时程的影响很小，但是，对位移时程的影响很大。通过对位移时程尾部的观察，对于记录051YAL130420113402，想得到合理的位移时程，低频截止频率应为0.08Hz，和频率搜索法确定的0.08Hz一致。

从图4可以看出无论是传统方法还是自动搜索算法，确定大部分强震动记录的低频截止频率都在0.1Hz左右，自动搜索算法得出的结果与传统较为接近。从图5和图6可知，由自动搜索算法确定低频截止频率的过程以及计算效率都是可行的。在实际海量强震动记录处理工作中，自动搜索算法的计算效率比传统方法有显著提高，节省大量人力。原则上只需要调整本算法的结束条件就可以适用于不同地震的强震动记录。

图5 记录051YAL130420113402频率搜索

2.4 误差统计与分析

自动搜索算法主要在张同宇（2016）关于低频截止频率的研究基础上发展而来，以下将张同宇关于低频截止频率的研究称为张同宇算法。自动搜索算法和张同宇算法主要区别是对于数据位移时程末尾段的定义和算法结束条件的不同。依据张同宇的研究，位移时程末尾段被定义为强震动记录末尾10s的长度。算法的结束条件是：

（1）位移时程末尾段10s的均值小于0.1cm；

（2）位移时程末尾段10s的均值小于0.04Hz滤波后位移时程末尾段10s均值的1/10；

（3）位移时程末尾段10s的均值小于对应位移时程峰值的1/10。

为评估自动搜索算法的有效性，利用自动搜索算法和张同宇算法对挑选出的609条强震动记录进行处理，确定每条记录的低频截止频率。为比较准确度，以传统方法为标准，将自动搜索算法和张同宇算法分别与传统方法获得的低频截止频率作差，得到误差统计结果。自动搜索算法和张同宇算法的误差统计图如图7所示，误差统计表如表1所示。可以看出，相对于传统方法，自动搜索算法所确定的低频截止频率误差基本上都在0.03Hz以内。

图6 记录051YAL130420113402滤波后速度、位移时程曲线

图7 自动确定低频截止频率误差统计

2.5 本文算法适用条件

从图7可知，有两条强震动记录低频截止频率的误差值在0.2Hz以上，这两条记录分别为051AXT080512142801和051CDZ130420080203，其加速度时程如图8所示。

对于强震动记录051AXT080512142801，根据于海英等（2009a）的研究可知，本记录的强震动台站受汶川主震的影响发生了永久位移，在汶川8.0级地震中有21组近场强震动台站都有不同程度的永久位移发生，由于本文篇幅限制，对以上21组三分量近场强震动记录的积分计算和滤波结果不一一列出。如图9左图所示，利用自动搜索算法确定的低频截止频率对该强震动记录进行带通滤波（低频截止频率0.29Hz）以后，两次积分得到的位移时程就会损失掉永久位移信息。对大地震近场获得的强震动记录经滤波处理会滤掉真实的地震动记录低频成分（于海英等，2009b）。所以，不仅该强震动记录不适合滤波，凡是有永久位移的强震动记录都不适合采用滤波进行零线校正处理，即不适合采用自动搜索算法确定低频截止频率。

对于强震动记录051CDZ130420080203，从图8右图可知，本记录数据不完整。记录前10s的最大值为0.055cm/s2，后10s的最大值为5.190cm/s2，震前和震后的地面震动差别比较大，所以判断本记录缺少末尾段。从图9右图可知，利用自动搜索算法确定的低频截止频率对该强震动记录进行带通滤波（低频截止频率0.29Hz）以后，两次积分得到的位移时程末尾段的均值较大。所以，不完整的强震动记录也不适合采用自动搜索算法确定低频截止频率。

综上分析，除了要避免选取具有奇异波形特征的强震动记录以外，还要求强震动记录满足以下条件时自动搜索算法才能准确确定低频截止频率：

（1）获得强震动记录的台站没有发生永久位移；

（2）强震动记录要完整，没有缺少末尾段的情况。

图8 051AXT080512142801和051CDZ130420080203加速度时程

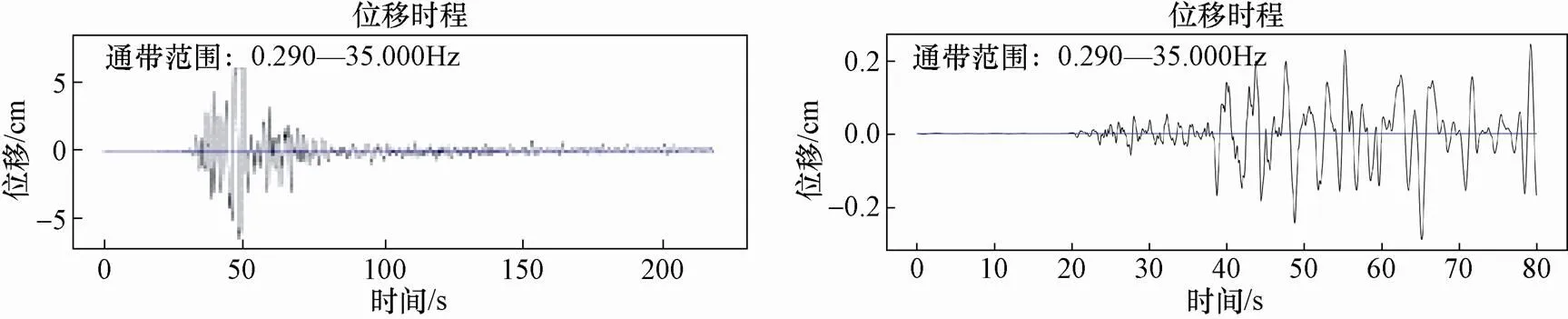
图9 051AXT080512142801和051CDZ130420080203位移时程

3 结语

本文通过分析选择低频截止频率应遵循的原则，以2008年汶川地震、2013年芦山地震获得的强震动加速度记录为例，提出一种低频截止频率自动搜索算法，利用统计学习方法中的损失函数来确定该算法流程的结束条件。该算法和传统方法确定的低频截止频率非常接近。目前，虽然确定地震动的低频截止频率只能对比传统方法，尚无标准可以参考，然而，本文为自动确定低频截止频率提供了新的量化途径。通过本文研究得出以下结论：

（1）本文提出的低频截止频率自动搜索算法准确性接近传统方法，计算效率比传统方法有很大提升，特别适合批量处理海量强震动记录；

（2）该算法适用于强震动台站产出记录完整且无永久位移的强震动记录；

（3）原则上只需要调整本算法的结束条件就可以适用于不同地震的强震动记录。

国家强震动台网中心，2014．中国强震记录汇报，第十七集，第一卷，芦山7.0级地震及余震未校正加速度记录．北京：地震出版社．

李航，2012．统计学习方法．北京：清华大学出版社．

谢礼立，李沙白，钱渠炕等，1983．我国强震记录处理和分析方法的若干特点．地震工程与工程振动，3（1）：1—14．

于海英，江汶乡，解全才，等，2009a．近场数字强震仪记录误差分析与零线校正方法．地震工程与工程振动，29（6）：1—12．

于海英，王栋，杨永强，等，2009b．汶川8.0级地震强震动加速度记录的初步分析．地震工程与工程振动，29（1）：1—13．

于海英，周宝峰，杨程等，2014．芦山7.0级地震及余震强震动记录初步分析．见：第九届全国地震工程学术会议论文集．哈尔滨：中国建筑学会，中国地震学会，中国地震工程联合会，153—160．

张军华，吕宁，田连玉等，2006．地震资料去噪方法技术综合评述．地球物理学进展，21（2）：546—553．

张同宇，2016．基于芦山地震强震动记录的数据处理技术研究．哈尔滨：中国地震局工程力学研究所．

中国地震局震害防御司，2008．中国强震记录汇报，第十二集，第一卷，汶川8.0级地震未校正加速度记录．北京：地震出版社．

周宝峰，2012．强震观测中的关键技术研究．哈尔滨：中国地震局工程力学研究所．

周宝峰，宋廷苏，于海英等，2014a．芦山强震记录中的奇异波形研究．地震工程与工程振动，34（S）：93—99．

周宝峰，温瑞智，谢礼立，2014b．强震记录中的“尖刺”现象初步研究．土木工程学报，47（S）：295—299．

Syun'itiro O., Tokiharu O., Shigeto H., et al., 1988. Data processing method for acceleration records and its application results. In: Proceedings of the Second Workshop on Processing of Seismic Strong Motion Records. Tokyo, 119—135.

Kenzo T., Sumio S., 1988. A method for correction of accelerograms. In: Proceedings of the Second Workshop on Processing of Seismic Strong Motion Records. Tokyo, 183—199.

Zhou B. F., Wang H. Y., Xie L. L., et al., 2015. Bizarre waveforms in strong motion records. Shock and Vibration, 2015: 630362.

Automatic Search Algorithm of Low Cut-off Frequency for Filtering Strong Motion Records

Yu Haiying1, 2）, Xu Xuan1, 2）and Zhang Tongyu1, 2）

1） Institute of Engineering Mechanics, China Earthquake Administration, Harbin 150080, China 2） Key Laboratory of Earthquake Engineering and Engineering Vibration of China Earthquake Administration, Harbin 150080, China

Aiming at the low efficiency of traditional methods to determine the low cut-off frequency for filtering strong-motion records, this paper proposes an automatic search algorithm to determine the cut-off frequency of low-frequency filters and uses the loss function in a statistical learning method to determine the end condition of the automatic search model flow. Based on strong-motion records obtained from the main shock and aftershocks of the 2008 Wenchuan earthquake and 2013 Lushan earthquake, we compare the results of automatic search algorithms and the low cut-off frequency identified by traditional methods, analyze the errors of automatic search algorithms, and propose principles and applicable conditions for their use. The results show that the algorithm improves computational efficiency significantly compared to traditional methods; in particular, the algorithm is suitable for the batch-processing of massive strong-motion records.

Strong motion records; Filter; Low cut-off frequency; Automatic search algorithm; Loss function

于海英，徐旋，张同宇，2018．强震动记录的低频截止频率自动搜索算法．震灾防御技术，13（1）：65—74．

10.11899/zzfy20180106

国家重点研发计划（2017YFC1500803），国家自然科学基金高铁联合基金资助项目（U1534202），黑龙江省自然科学基金（E2015070），国家自然科学基金青年项目（51308517）

2017-11-20

于海英，男，生于1962年。研究员。主要从事强震动观测与数据处理技术方面研究。E-mail：haiyingyu@126.com

徐旋，男，生于1992年。硕士研究生。主要从事强震动数据处理技术方面研究。E-mail：xu_dexuan@outlook.com