一种动态加权模糊聚类算法的研究

刘 锐，张 宁

（北京交通大学 计算机与信息技术学院，北京 100044）

聚类是按照一定规则对某一事物进行区分和归类的动态过程，在整个过程中，没有专家知识的指导，没有先验知识的支持，聚类仅仅依靠事物之间的“相似度”作为划分的标准[1]。是一种典型的无监督式学习，相较于监督式学习，数据标签是区分两者的最重要指标。

FCM算法，即模糊C均值聚类算法，是一种典型的软化分聚类算法，舍弃了硬划分中非0即1的方法，采用一种划分矩阵的输出形式来表示某一样本数据隶属于某一类的概率。FCM算法以其“模糊”的输出特点在数据挖掘、模式识别等领域应用广泛，而且，伴随高铁动车组的发展，FCM聚类逐步应用于动车组故障关联关系分析、健康状态评估等方面[2]。

FCM算法的缺陷也是十分明显[3]。在选取初始聚类中心时具有随机性导致聚类易陷入局部极小，并且，FCM对于样本数据中的噪声与孤立点特别敏感，会导致影响聚类质量。本文提出了一种基于FCM的动态加权模糊聚类算法，利用遗传算法全局搜索能力强的特点，自适应选取最优初始聚类中心，并且结合局部异常因子（LOF，Local Outlier Factorl）密度加权策略，降低噪声点对聚类的影响。经通用数据集验证，优化后的算法有效提高了聚类质量和准确度。

1 模糊聚类

1.1 聚类划分约束

对象特征输入表示X={x1, x2,…, xN}归为c个子集{x1, x2,…, xc}，其中，xk表示对象ok的特征输入，xi是X中属于第i输入类的对象子集，其对应的归类输入的类外延表示由划分矩阵U=[uik]c×N表示，其中，uik表示对象ok属于第i个输入类的隶属度，uik≥0，U通常被称为隶属矩阵。根据隶属度的不同，产生了不同的划分约束[4]。

（1）硬划分 ：

（2）软划分 ：

（3）可能性划分

1.2 FCM算法

FCM算法的表述为[5]：设样本数据集为x={x1,x2, x3, …, xn}，共包含n个样本，现在需将其分为k类，则在样本数据集x中必存在一个k×n的分类矩阵 U(x)=[uij]，i=1, 2, …, k ；j=1, 2, …, n，uij表示样本j属于聚类i的隶属度，满足式（1）：

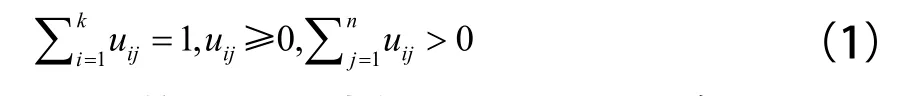
FCM算法是通过求出最佳分类矩阵U(x)以及聚类中心矩阵V(x)，使得总类内方差达到极小。

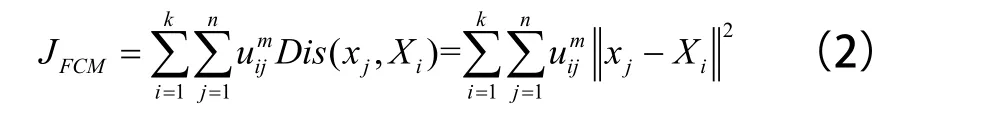
其中，Xi表示第i类的聚类中心；Dis(xj, Xi)表示样本点xj到类中心Xi的距离，FCM中最常用的距离公式是欧氏距离；中m表示影响聚类性能的加权系数，取值范围为m≥1。

一个好的聚类应该使得总类内方差JFCM在的约束下到达全局最小。通过迭代运算，解得：

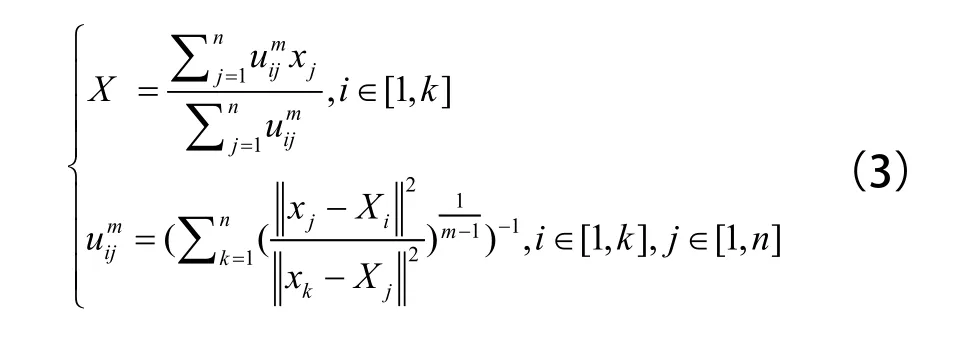
1.3 聚类评价指标

（1）DB指数，又称为分类适确性指数[6]。计算公式为：

表示任意两类别的类内距离的平均距离除以两聚类最小中心距离。DB指数越小意味着类内距离越近，类间距离越远，聚类质量越好。

（2）聚类准确度[7]。是对最终聚类划分正确度的评价。准确度指数的计算公式为：

k表示聚类个数，N表示样本点总个数，ac表示每一个类中划分正确的个数。为了保证结果的准确，通常会多做几次实验取均值来表示最终的准确度，H表示实验次数。

2 GA-FCM算法

FCM算法在选取初始聚类中心时具有随机性，在迭代时是以一种类似于爬坡似的方法逐步迭代，是一种局部搜索最优解的方法[8]，因而易导致聚类结果极易陷入局部极小值。遗传算法是一种应用广泛的全局搜索方法，利用选择、交叉和变异操作，通过不断的迭代，逐步逼近最优解，从而避免陷入局部最优，因而可以和FCM算法进行良好互补[9]。这样，既能发挥遗传算法全局搜索能力强的优势，又可以结合FCM善于局部搜索的特点，可以很好地解决聚类问题中对初始点过于敏感这一缺陷。本文将遗传算法优化FCM算法称之GA-FCM算法。

2.1 编码

本文采用16 bit二进制编码。假设原始数据集有d个维度，m行数据，则可以表示为：

若将DataSet划分为k类，则k个初始聚类中心可以表示为：[(v11,…,v1d),(v21,…,v2d),(vk1,…,vkd]，采用16 bit二进制编码，对应的编码精度为：

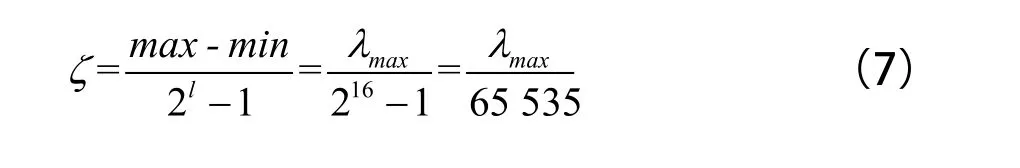
解码公式为：

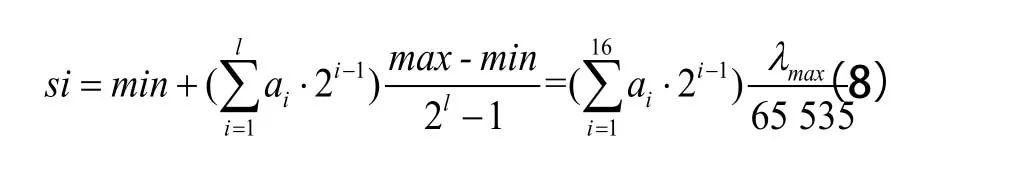
2.2 确立适应度函数

GA-FCM算法最核心步骤之一就是利用FCM的类内总方差函数构造遗传算法的适应度函数，其中的关系要表示为适应度函数越大，类内总方差越小，则聚类结果越优。所以将适应度函数定义为：

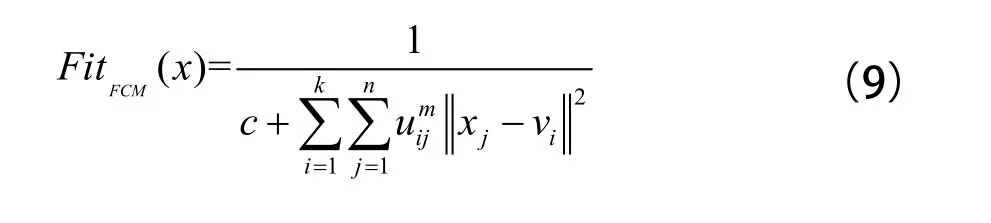
其中，c∈[1, 2]。

2.3 基于轮盘赌的选择算子

计算当前第i代的个体染色体的选择概率以及当前累计概率：

产生N个随机数λi∈[0,1](i=1, 2,…, N)。若满足 λi＜P1，则选择第一个个体 ；若满足 Pi–1＜λi＜Pi，则选择第i个个体。直至选择出N个个体。

2.4 根据适应度值动态确定交叉算子

本文舍弃随机生成交叉算子法，采用一种自适应法，根据种群的适应度函数值来计算交叉概率，整体原则就是如果该染色体的适应度值较小，则它发生交叉的概率越大；如果适应度大，则交叉概率越小。这样在保证种群丰富度的同时，还可以尽量避免优良个体被破坏。交叉概率计算公式为：

其中，pmax表示最大交叉概率，为[0.8, 0.9]之间的随机数；pmin表示最小交叉概率，为[0.2, 0.3]之间的随机数；Fitmax表示的当前种群中最大的适应度值； Fitavg表示当前种群中的平均适应度值；Fit'max表示发生交叉的两个染色体中较大的适应度值。

2.5 根据适应度值动态确定变异算子

变异率是指个体染色体编码序列中每一位发生改变的概率。因为变异的不稳定性，所以说变异概率很低，通常的取值范围为[0.000 1, 0.1]。本文中，根据适应度值确定变异概率，若当前染色体的适应度值很低，则有较高变异率；反之，若当前个体的适应度值很高，则有较低变异率。计算公式如下：

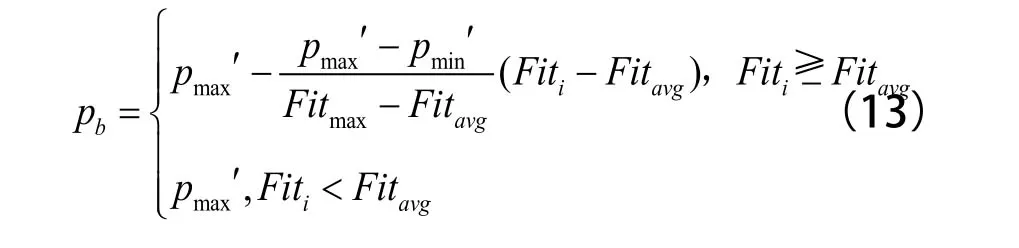
Fiti表示当前染色体的适应度值。pmax'表示最大变异概率，通常为0.1；pmin'为最小变异概率，通常为0.000 1。

3 基于LOF的加权优化算法

样本数据中的离群点与噪声点对聚类的影响如图1所示，由于噪声点的干扰，类中心的最终位置往往不在合理区域。针对FCM算法对数据样本中的离群点与噪声点过于敏感，本文采用LOF算法进行优化，从而保证类中心最后位于样本区域密度大的位置。LOF是通过计算样本区域密度来鉴别噪声点的算法[10-11]。

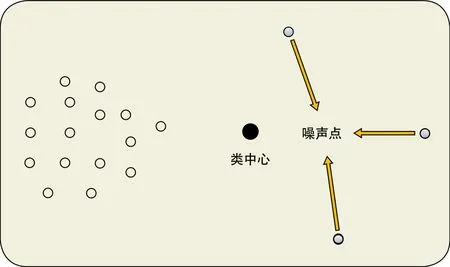
图1 噪声点影响类中心示意图

算法描述为：

（1）计算样本中每个对象p与其他对象的欧氏距离 d(p, o)。

（2）计算对于点p的第k 距离dk(p)，即dk(p)=d(p, o)；定义点p的第k邻域为Nk(p)，表示p的第k距离以内的所有点，满足|Nk(p)|≥k。

（3）计算点o到点p的第k可达距离，为：

（4）计算点p的可达密度，表示点p的第k邻域内点到p的平均可达距离的倒数。具体公式为：

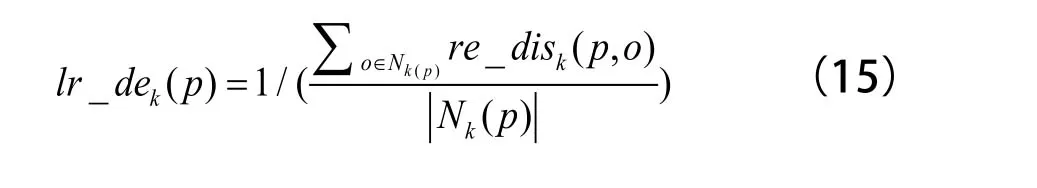
（5）计算局部离群因子，定义为点p的邻域点Nk(p)的局部可达密度与点p的局部可达密度之比的平均数，公式为：

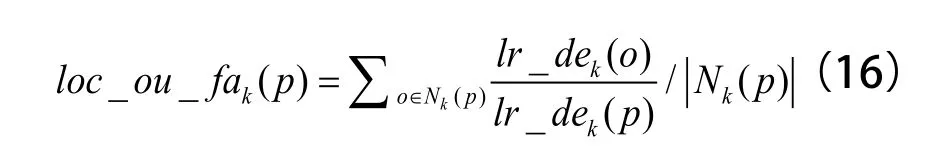
LOF算法对于样本异常点的监测是根据上述求解出的各个数值的大小来进行判别，理论上讲，数据异常点是不能剔除的，因为剔除异常点会严重破坏原始数据的完整性，而影响最终的聚类划分，因此，本文将LOF与GA-FCM结合，可以实现聚类中心点最终停留在样本密度大的区域，降低数据噪声点对于聚类的影响。

LOF算法中最终求解出的loc_ou_fak(p)，可以表示区域密度，即：

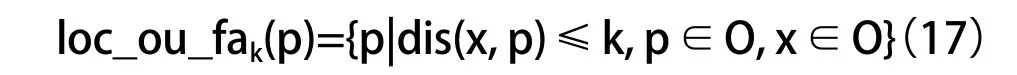
该值越大，说明点p周围的区域密度越大；该值越小，说明点p周围区域密度越小，则其越可能是离群点。

则FCM算法中的JFCM可以重新定义为：

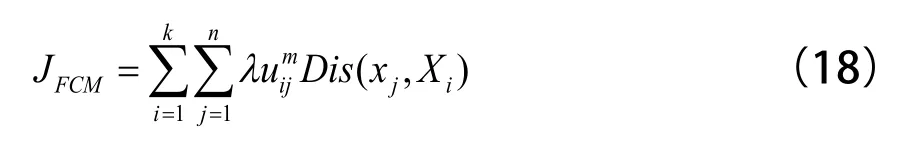
GA-FCM算法中适应度函数也重新定义为：

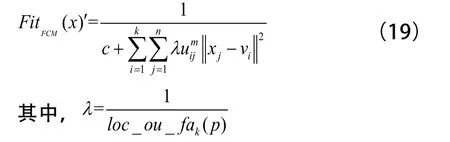
这样可以保证在样本密度大的区域附近，JFCM变小，FitFCM(x)'变大；反之，在样本密度小的区域附近，FitFCM(x)'变小，JFCM会变大，则不会收敛。便可以保证聚类中心停留在样本密度大的区域，有效提高聚类的合理性。因此，本文将这种通过遗传算法与LOF加权共同优化FCM的算法称之为WG-FCM算法。

4 实验结果与分析

4.1 实验描述

本文试验平台：Intel(R) Core(TM) i5-2450M CPU@2.50 GHZ，RAM 4 G，Windows 7操作系统和Matlab R2012(a)。实验数据集：UCI数据库上的Iris、Wine、Vowel共3组数据作为测试数据集进行验证。UCI数据库是国际通用的用于进行数据挖掘、机器学习等算法验证的公开数据库。测试数据集信息如表1所示。

4.2 聚类对比分析

本文选用改进的FCM算法与标准的FCM算法对上述3组数据集进行实验，如表2所示的是3种算法聚类准确率对比。

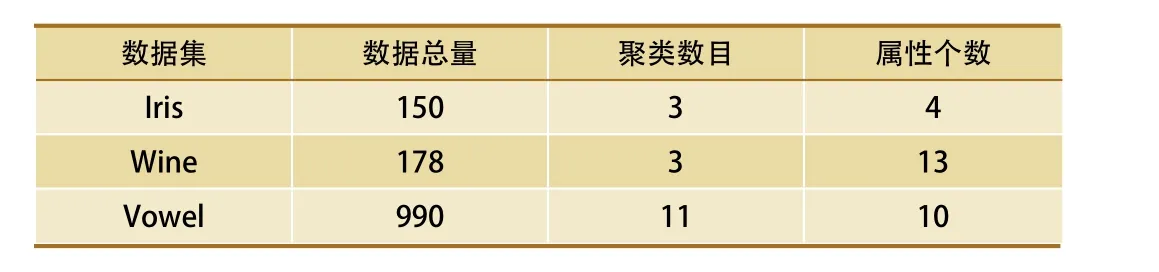
表1 测试数据集信息表

由表1与表2可以看出，虽然当数据集中属性维度越多时，聚类准确率会下降。但是纵向比较而言，WG-FCM还是可以有效提高聚类准确性。

从表3中可以看出，GA-FCM与WG-FCM求解出的DB指数均比原始FCM的低，WG-FCM算法的DB指数最小，表示可以有效提高聚类质量，让聚类变得更加合理。

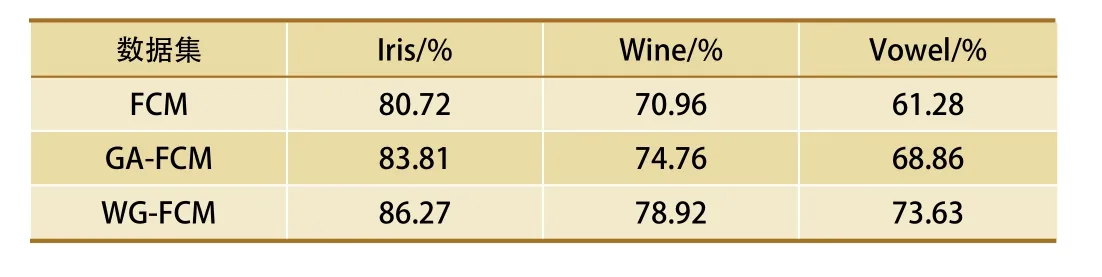
表2 3种算法准确率对比

从表4中可以看出，WG-FCM算法的收敛速度明显高于原始FCM算法，相较于GA-FCM算法也是有所提升的，证明了FCM算法通过结合遗传算法与LOF加权后能够明显提高全局搜索最优值的速度。

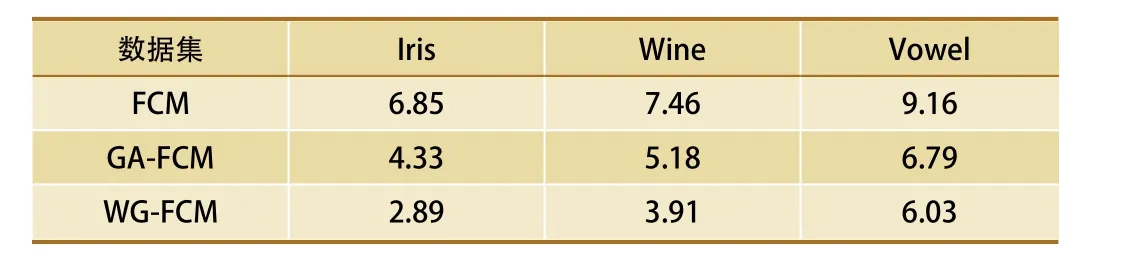
表3 3种算法DB指数对比

5 结束语

本文针对原始FCM算法中心点选取具有随机性的缺陷，通过遗传算法优化选取初始中心点，并且，根据适应度值计算交叉率与变异率，使之具有动态性；对于数据异常点过于敏感的问题，结合LOF算法，通过添加权重值重新构造FCM算法的准则函数，减少数据噪声点对于聚类的影响，保证最终聚类中心停留在样本点密度大的区域，通过UCI数据库上的标准数据证明，WG-FCM算法可以有效提高聚类质量和准确度。

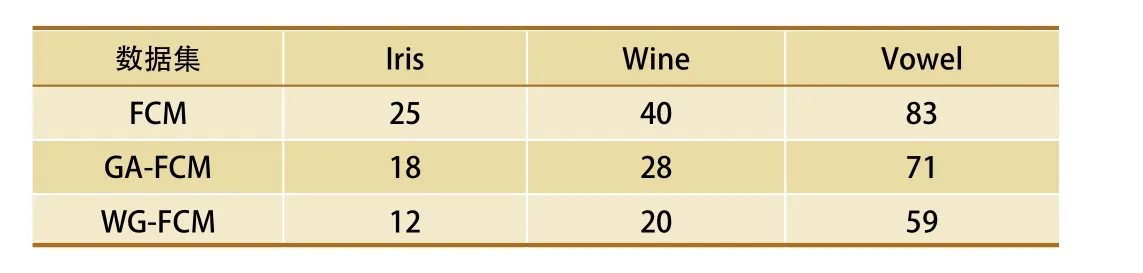
表4 3种算法平均收敛代数对比

[1]伍育红.聚类算法综述[J].计算机科学，2015，42（Z6）：491-499.

[2]欧阳喜德，黄地龙. 基于模糊聚类的数据挖掘方法与应用[J].铁路计算机应用，2008，17（4）：13-16.

[3]朱 然，李积英. 几种优化FCM算法聚类中心的方法对比及仿真[J]. 计算机技术与发展，2015（5）：17-20.

[4]付 强，袁 磊. 基于聚类分析及SVM的DMI机车信号自动识别[J]. 铁路计算机应用，2015（8）：46-49.

[5]朴尚哲，超木日力格，于 剑. 模糊C均值算法的聚类有效性评价[J]. 模式识别与人工智能，2015，28（5）.

[6]胡嘉骏，侯丽丽，王志刚，等. 基于模糊C均值隶属度约束的图像分割算法[J]. 计算机应用，2016，36（1）：126-129.

[7]Yang S, Kim J, Chung M. A prediction model based on Big Data analysis using hybrid FCM clustering[C]// Internet Technology and Secured Transactions. IEEE, 2015:337-339.

[8]Vimali J S, Taj Z S. FCM based CF: An efficient approach for consolidating big data applications[C]// International Conference on Innovation Information in Computing Technologies. IEEE,2016:1-7.

[9]李 赢, 舒乃秋. 基于模糊聚类和完全二叉树支持向量机的变压器故障诊断[J].电工技术学报，2016，31（4）：64-70.

[10]肖林云，陈秀宏，林喜兰. 特征加权和优化划分的模糊C均值聚类算法[J]. 微电子学与计算机，2016，33（10）：143-146.

[11]Varghese J, Subash S, Khan M S, et al. An efficient LOF-based long-range correlation filter for the restoration of salt and pepper impulse corrupted digital images[J]. Turkish Journal of Electrical Engineering & Computer Sciences, 2016, 24(4):2429-2441.