定子匝间短路位置对发电机定子振动特性的影响

何玉灵 彭勃 万书亭

摘要： 对气隙静偏心和定子短路故障的相对位置对定子振动特性的影响进行解析分析、数值计算和实验研究。首先推导得到了包含定子绕组短路位置信息的作用于定子单位面积的磁拉力解析表达式，分析得到了定子短路位置对磁拉力的影响；然后建立了算例发电机正常运行、气隙静偏心故障、气隙静偏心与定子匝间短路复合故障下的有限元模型，对不同短路位置下的定子磁拉力进行了仿真计算。并实测了MJF306型故障模拟发电机定子不同短路位置的定子振动信号，三者结果相互吻合。结果表明：气隙静偏心与定子匝间短路复合故障下，同等故障程度时，发电机定子振动幅度与短路位置有关，短路位置越接近最小气隙处，各倍频振动幅度越大，越远离最小气隙处，各倍频振动幅度越小。关键词： 故障诊断； 发电机； 定子振动； 气隙静偏心； 定子匝间短路

中图分类号： TH165.3； TM311文献标志码：A文章编号：10044523（2017）04067909

DOI：10.16385/j.cnki.issn.10044523.2017.04.020

引言

由于制造和运行等原因，发电机定转子之间的气隙或多或少存在不均匀状况（即气隙偏心），当偏心程度大于10%时，将会引起发电机的剧烈振动，严重时，将会造成定子铁芯变形、绕组损坏等事故[1]。文献[23]研究了气隙偏心故障下，发电机三相绕组的电流或电压值的变化；文献[45]分析气隙偏心下发电机的定子并联支路环流特性，并提出相应识别方法。

定子绕组匝间短路作为运行人员主要关注的电气故障之一也时有发生，是一种危害较为严重，修复费用较高的故障[6]。文献[7]分析了定子短路匝间对发电机感应电动势的影响，通过故障前后电势的差异来识别故障；文献[8]分析了定子匝间短路故障下定子并联支路环流特性的变化，并讨论了短路参数变化对环流特性的影响；文献[9]在发电机气隙中安装探测线圈，通过分析端口电压频率特征差异判断对定子匝间短路故障。

事实上，气隙静偏心是普遍存在的，定子匝间短路故障发生时，发电机往往处于气隙静偏心与定子匝间短路的复合故障状态。同时由于发电机是机电耦合的整体，故障将引起气隙磁场和作用于定转子的磁拉力变化，从而激励发电机定转子振动，并且振动信号测试更加便捷。因此已有文献研究故障下的振动特性，文献[10]研究了气隙靜偏心和定子短路复合故障的定子振动特性及其变化规律，但没有考虑故障位置对其特性的影响。文献[11]研究了考虑气隙偏心时发电机定子匝间短路位置对电磁转矩波动特性的影响。

本论文将在文献[1011]基础上，首次对气隙静偏心和定子短路故障的相对位置对定子振动特性的影响进行解析分析、数值计算和实验研究，分析结果是对发电机气隙静偏心与定子匝间短路复合故障诊断的一个重要补充，具备积极意义。

1定子振动特性分析〖*2〗1.1定子受力分析发电机的定子由定子铁芯、绕组、机座、端盖等部件组成，其中定子铁芯是磁拉力激励的主要部件。定子铁芯单位面积磁拉力表达式如下qαm，t=Bαm，t22μ0=fαm，tΛαm，t22μ0（1）式中B为气隙磁密，αm为气隙周向角，Λ为单位面积气隙磁导，f为气隙磁势，μ0为真空磁导率。

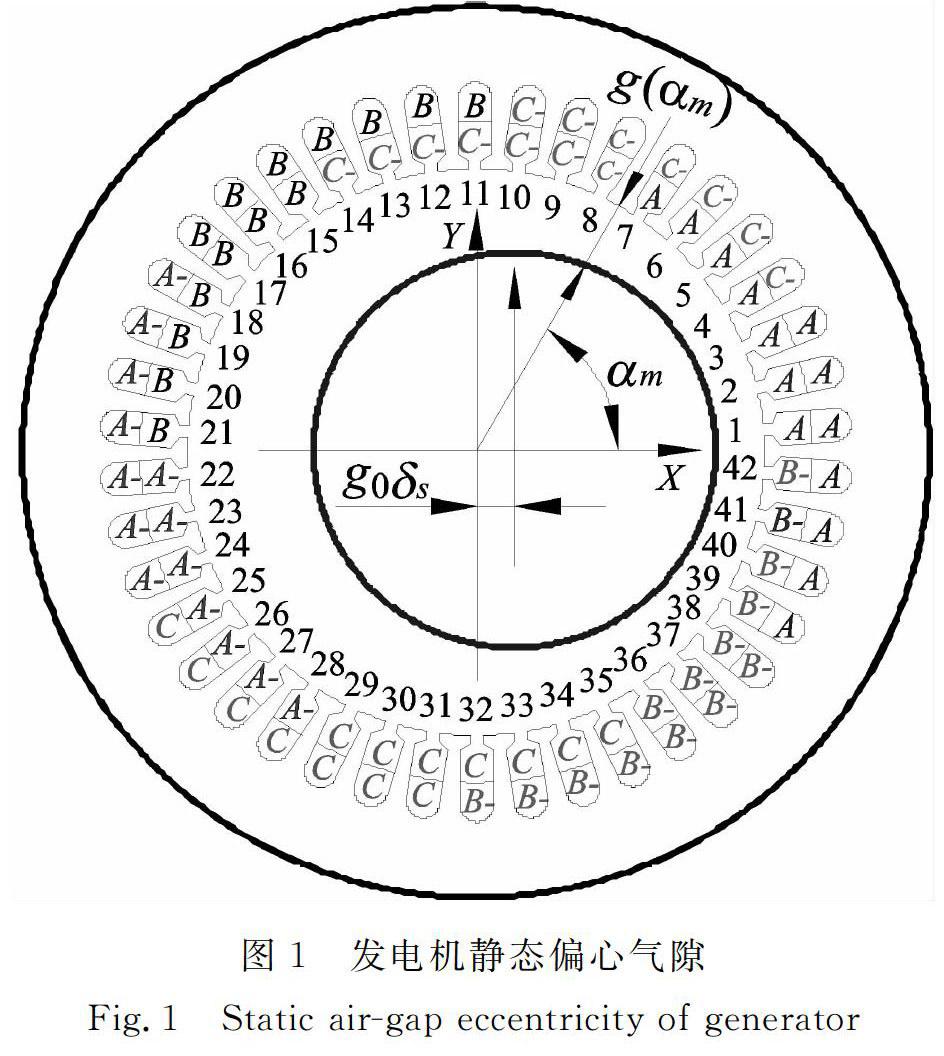
文献[10]在推导气隙静偏心与定子匝间短路复合故障下的发电机气隙磁势时，认为短路环电流产生的脉振磁势恒定，忽略了定子短路点与静偏心的相对位置对定子振动的影响。事实上，如图1 所示，以气隙最小处作为原点，气隙静偏心时，气隙磁密会随着气隙周向角的变化而变化。因此，定子匝间短路位置不同（定义定子绕组短路位置角α′m为定子绕组短路匝中心位置与气隙最小处的夹角），短路环电流值也将不同，进一步导致其产生的脉振磁势幅值有所不同。

图1发电机静态偏心气隙

Fig.1Static airgap eccentricity of generator

作为改进，本文假设在气隙最小处发生定子匝间短路（短路位置角α′m为0度），设短路环中附加环流产生的脉振磁势为Fd，且幅值最大（磁导最大），故短路位置产生的脉振磁势幅值与最大脉振磁势幅值的比为ρ=fdFd=1-δs1-δscosα′m（2）式中g0为平均气隙，δs为相对静偏心值。以42槽汽轮发电机为例，假设最小气隙位置位于1槽，则当定子匝间短路匝中心位置在1槽至42槽时，ρ值变化趋势如图2所示。

图2短路匝中心位于不同槽下ρ值变化趋势

Fig.2Developing trend of ρ when interturn shorted center is in different slots

从式（2）与图2中可看出，定子匝间短路位置越接近最小气隙处时产生的脉振磁势幅值越大，反之，定子匝间短路位置越远离最小气隙处时产生的脉振磁势幅值越小。此外，ρ值大小还与偏心程度有关系，偏心程度越大则上述规律越明显。忽略高次谐波，不同位置的定子匝间短路产生的脉振磁势可表示为fd（αm，t）=ρFdcosωtcospαm=

ρFd+cos（ωt-pαm）+ρFd-cos（ωt+pαm）（3）式中p为发电机极对数，ω为电角频率。

第4期何玉灵，等： 定子匝间短路位置对发电机定子振动特性的影响振 动 工 程 学 报第30卷对比文献[10]中公式可发现，考虑气隙静偏心后，式（3）中的第1项以同步速与转子同向旋转，在转子绕组中不感应附加谐波电势，第2项以同步速与转子逆向旋转，将在转子绕组中感应2倍频电流值ρIf2。以基频转速反向旋转的电枢反应磁势最大幅值变为ρFs1-，以3倍频转速正向旋转的电枢反应磁势最大幅值变为ρFs3+，最终影响定子磁拉力各次谐波幅值，详细推导过程可见文献[10]。根据上述内容对定子磁拉力主要谐波成分幅值做出修改，如表1所示。直流分量（0 Hz）是常值，不会激励定子产生振动，不列入表中。

分析表1可知，正常运行和气隙静偏心单故障下，作用于定子单位面积的磁拉力主要谐波成分为2次谐波（100 Hz），但静偏心下谐波幅值较正常情况要大。复合故障下，定子磁拉力主要谐波成分为2次谐波（100 Hz）、4次諧波（200 Hz）、6次谐波（300 Hz）。复合故障下定子磁拉力各次谐波幅值比单故障大。此外，复合故障下，当保持气隙静偏心程度与定子匝间短路程度不变时，短路位置越接近最小气隙处，定子磁拉力2次谐波、4次谐波以及6次谐波幅值增大越多，反之越少。各次谐波幅值随周期变化，会激励定子产生的相应倍频振动。

1.2基于有限元法求解单位面积磁拉力

由于电机磁场计算时常忽略端部效应，认为磁场轴向均匀分布，故采用二维磁场进行计算。由上文所述，定子振动的本质激励源为单位面积磁拉力，计算定子所受磁拉力时应选取定子内圆上的一点作为求解点，最终求解得到的磁拉力即为单位面积磁表1不同情况下定子磁拉力各次谐波成分幅值

Tab.1Stator electromagnetic force amplitude under different conditions

成分运行状态幅值表达式2次

谐波正常I2f0N2Λ20/4μ0静偏心0.5I2f0N2+0.5F2s-If0NFssinΛ20+Λ2s+2Λ0Λs/2μ0复合故障[（ρIf0If2N2+ρFs1+Fs1-+ρFs1+Fs3++ρIf0NFs1-+If0NFs1++ρIf2NFs1++ρ2If2NFs1-+ρIf0NFs3++

0.5ρ2If2NFs3++ρ2Fs1-Fs3++0.5F2s1++0.5ρ2F2s1-+0.5I2f0N2+0.5ρ2I2f2N2）（Λ20+Λ2s/2）+

0.25（ρ2F2s1-+F2s1++ρ2I2f2N2+I2f0N2+2ρIf0If2N2+2If0NFs1++2ρIf0NFs1-+2ρIf2NFs1++

2ρ2If2NFs1-+2ρIf0NFs3++ρ2If2NFs3++2ρFs1+Fs1-+2ρFs1+Fs3++2ρ2Fs1-Fs3+）Λ2s+

（F2s1++ρ2F2s1-+2ρFs1+Fs1-+2ρ2Fs1-Fs3++2ρFs1+Fs3++I2f0N2+ρ2I2f2N2+2ρIf0If2N2+

2If0NFs1++2ρIf2NFs1++2ρIf0NFs1-+2ρ2If2NFs1-+2ρIf0NFs3++ρ2If2NFs3+）Λ0Λs]/2μ04次

谐波正常—静偏心—复合故障[（ρ2I2f2N2/2+ρIf0If2N2+ρIf2NFs1++ρ2If2NFs1-+ρ2If0NFs3++ρ2If2NFs3++2ρ2Fs1-Fs3++

2ρFs1+Fs3+）（Λ20+Λ2s/2）/2+（2ρIf0If2N2+ρ2I2f2N2+ρ2If2NFs1++2ρ2If2NFs1-+

4ρIf0NFs3++2ρ2If2NFs3++4ρ2Fs1-Fs3++4ρFs1+Fs3+）Λ2s/8+（ρ2I2f2N2/2+ρIf0If2N2+

2ρIf0NFs3++ρIf2NFs1++ρ2If2NFs1-+ρ2If2NFs3++2ρ2Fs1-Fs3++2ρFs1+Fs3+）Λ0Λs]/2μ06次

谐波正常—静偏心—复合故障[ρ2（F2s3++I2f2N2/2+If2NFs3+）Λ2s+ρ2（4F2s3++4If2NFs3++2I2f2N2）Λ0Λs+

ρ2（2F2s3++2If2NFs3++I2f2N2）（Λ20+Λ2s/2）]/8μ0

拉力。本文使用电机有限元软件Ansoft作为计算工具，仿真运行后，可以直接获取发电机气隙磁密在所选求解点处X轴分量Bx（αm，t）与Y轴分量By（αm，t），再通过Field Calculator对公式（4）编辑并进行计算，即可求得求解点处径向气隙磁通密度Bαm，t=Bxαm，tcosθ+Byαm，tsinθ（4）式中θ为求解时使用的柱坐标。

联立公式（1），（4），最终得到作用于发电机定子的单位面积磁拉力的表达式为qαm，t=Bxαm，tcosθ+Byαm，tsinθ22μ0（5）再次通过Field Calculator对公式（5）编辑并进行计算，求得单位面积磁拉力，并分析频率成分。

2有限元仿真与动模实验〖*2〗2.1实验设备与测试方法本文利用MJF306故障模拟发电机进行实验验证，总体外观如图3（a）所示。该型模拟发电机的定转子均无法移动，不能对气隙静偏心故障进行模拟。但考虑到制造精度、装配误差以及长时间运行等因素的影响，判断实验室发电机可能会存在一定程度的气隙静偏心。利用高精塞尺对定转子间的气隙进行实际测量，如图3（b）所示，发现该模拟发电机励端视图上偏左22°区域为气隙最小处，gmin=0.80 mm，下偏右22°区域为气隙最大处，gmax=0.90 mm，偏心示意图如图3（c）所示。此外，该型模拟发电机引出多个定子绕组短路抽头，短路抽头设置及其接线盘如图3（d），（e）所示。其中，定子C1支路短路5%抽头C12所在绕组位置与气隙最小处位置机械夹角α′m=111°（短路位置远离最小气隙处），B1支路短路5%抽头B12所在绕组位置与气隙最小处位置机械夹角α′m=60°，C2支路短路5%抽头C22所在绕组中心与气隙最小处机械夹角α′m=2°（短路位置接近最小气隙处）。分别短接抽头C12与C22，即可模拟静偏心程度与短路程度一定而短路位置不同的复合故障。

实验过程，并网运行，励磁电流If0=1.3 A，P=10 kW，Q=4 kVar。采用CD21C型振动速度传感器对发电机定子铁芯的竖直方向振动进行测取，其灵敏度为30 mV/mm/s，如图3（f）所示。将振动速度传感器的输出端接入至U60116型采集仪，采样频率为5 kHz，实验测试系统如图3（g）所示。模拟实验分4组，具体方案如下：

1） 不短接抽头，模拟气隙静偏心单故障，采集定子振动数据。

2） 短接抽头C12，模拟气隙静偏心与定子匝间短路复合故障1，采集定子振动数据。

3） 短接抽头B12，模拟气隙静偏心与定子匝间短路复合故障2，采集定子振动数据。

图3MJF306型故障模拟机组

Fig.3MJF306 type fault simulating generator set

4）短接抽头C22，模拟气隙静偏心与定子匝间短路复合故障3，采集定子振动数据。

2.2有限元建模与仿真

本文对MJF306型隐极故障模拟发电机进行有限元建模仿真，其相关参数如表2所示。表2MJF306型故障模拟发电机主要参数

Tab.2Primary parameters of MJF306 type generator

参数名称参数值额定容量30 kVA额定电压400 V转速1000 r/min定子槽数54槽转子槽数30槽定子每槽匝数72匝转子每槽匝数88匝气隙径向长度0.85 mm在有限元软件Ansoft的RMxprt电机模块环境下，根据表2输入相关参数，即可自动生成发电机有限元模型，且该模型能对发电机正常运行状态进行仿真。气隙静偏心故障的仿真方法是使转子轴心与定子轴心产生偏移。将RMxprt模块自动生成的发电机有限元模型导入Maxwell 2D模块，按照图3（c）所示偏心情况对发电机定子铁芯、定子绕组及OuterRegion进行移动，即可得到气隙静偏心故障下的发电机有限元模型，且与实验机组的偏心情况保持一致。定子短路为电气故障，不会对定转子的气隙间距产生影响，故直接对气隙静偏心故障下的发电机有限元模型进行二次修改即可。利用Ansoft Maxwell Circuit Editor软件绘制定转子外电路，如图4（a）所示，并将其导入Maxwell 2D模块，使发电机有限元模型的绕组与外电路相耦合。以B相绕组为例，图中LB1，LB2，LB3分别为发电机B相第一条支路绕组，RB1为B相第一条支路总图4发电机数值仿真分析模型

Fig.4Analysis model of turbogenerator for simulation

电阻，RB为B相负载电阻。LshortB3为短路故障下LB3中被短路的线圈，RB3S为LshortB3电阻，RB3为短路故障下LB3中未被短路的线圈电阻。SB3为压控开关，R_SB3为SB3的电阻。V_SB3为脉冲电压源， -1 V为脉冲电压源的初始电压，1 V为脉冲电压源的峰值电压，用来提供开关动作电压。ShortModel_SB3为SB3的模型元件，压控开关模型元件需要与压控开关一起使用。DC是励磁电流源。RA是为保证电流源所提供电流全部通过转子绕组而添加的电阻，与绕组本身结构无关。LF1，LF2，LF3，LF4，LF5，LF6分别是转子绕组。Rf是转子绕组的总电阻。

至此，建立了气隙静偏心与定子短路复合故障下的发电机有限元模型，二维分析模型如图4（b）所示，有限元网格剖分情况如图4（c）所示，气隙及绕组槽内网格最大边长为0.008 mm，得到10710个网格单元。

仿真过程中，对转子绕组施加1.3 A电流，与实验过程保持一致。3个开关SB3，SC3和SC6设置有相应的控制电路，如图4（a）所示。SB3，SC3和SC6均不闭合时，仿真气隙静偏心单故障；SC3闭合时，短路绕组LshortC3被短接，仿真复合故障1；SB3闭合时，短路绕组LshortB3被短接，仿真复合故障2；SC6闭合时，短路绕组LshortC6被短接，仿真复合故障3。

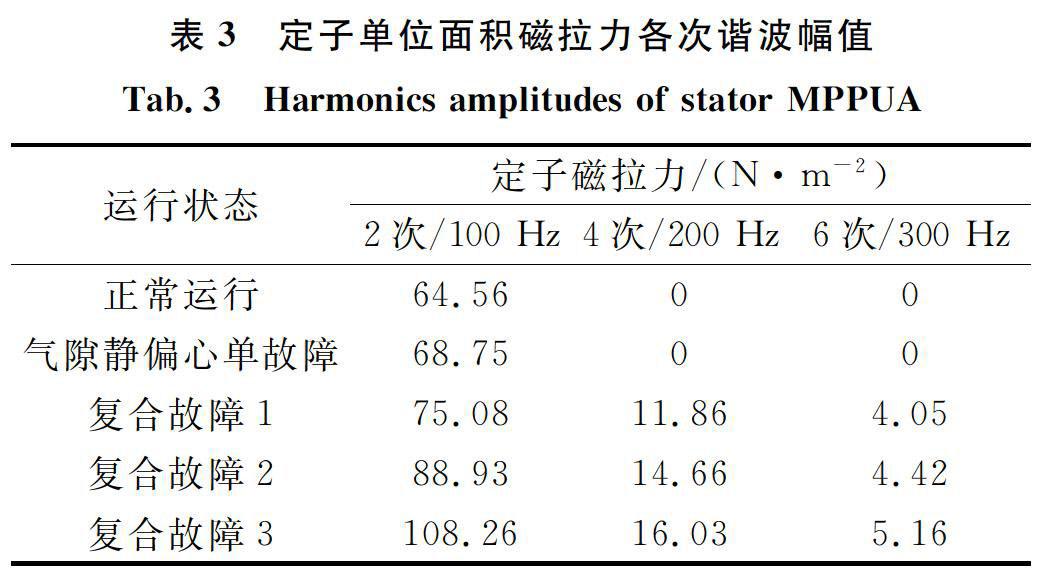
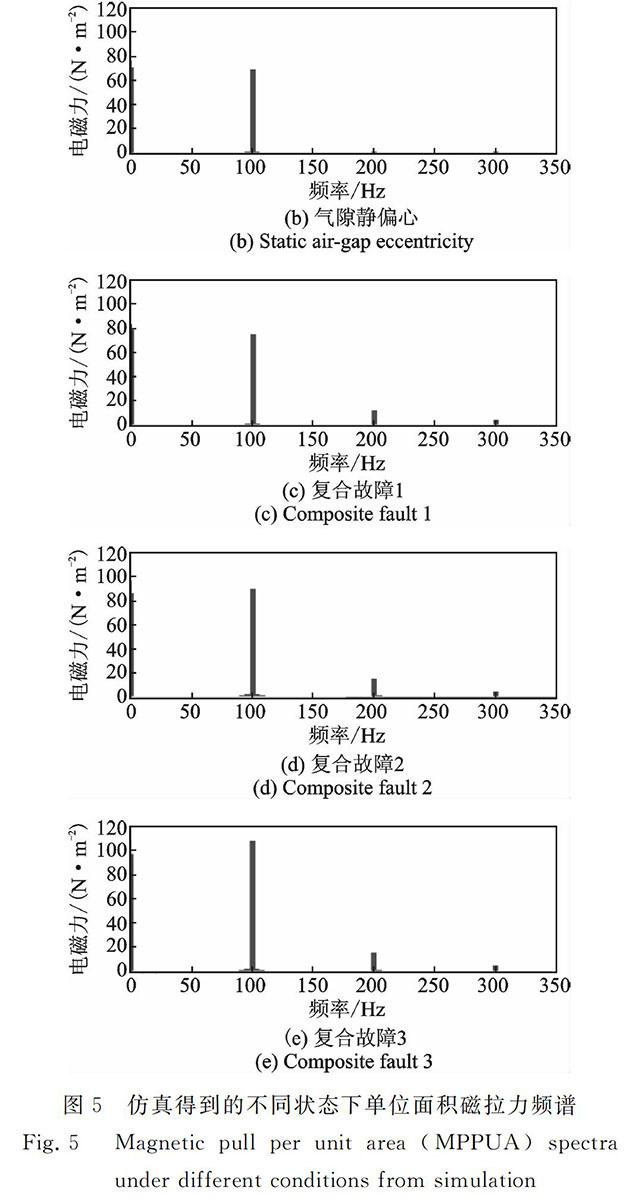
3结果分析与讨论〖*2〗3.1有限元仿真结果Ansoft仿真计算得到3种运行状况下的单位面积磁拉力频谱，如图5和表3所示。

图5仿真得到的不同状态下单位面积磁拉力频谱

Fig.5Magnetic pull per unit area （MPPUA） spectra under different conditions from simulation

表3定子單位面积磁拉力各次谐波幅值

Tab.3Harmonics amplitudes of stator MPPUA

运行状态定子磁拉力/（N·m-2）2次/100 Hz4次/200 Hz6次/300 Hz正常运行64.5600气隙静偏心单故障68.7500复合故障175.0811.864.05复合故障288.9314.664.42复合故障3108.2616.035.16

从图5和表3可以看出，复合故障2的磁拉力各次谐波幅值都大于复合故障1，与解析分析结果一致。

3.2实验测试结果

实验室故障模拟发电机存在气隙静偏心，无法采集到严格无偏心情况下的定子振动数据。作为对比，本文调取了2002年不设置短路故障采集的定子振动数据，并对其与2015年采集的数据做傅里叶变换，分析发电机振动特征，原始频谱如图6所示。

由文献[10]可知，发电机气隙静偏心和定子短路复合故障下定子振动的特征频率成分为100，200与300 Hz，而从图6可看出，原始定子振动信号中故障特征振动频率成分完全被环境图6原始定子振动频谱

Fig.6Original stator vibration spectra

噪声淹没，无法对发电机故障进行诊断与识别。因此，本文利用文献[12]提出的一种基于正弦结构元素的自适应改进TopHat变换算法，旨在有效消除原始信号中环境噪声，同时增大故障特征振动频率的幅值，去噪过程中4组信号采用相同的处理参数，对应的算法流程如图7所示。

图7算法流程图

Fig.7Algorithm flow chart

該算法主要步骤如下：

（1） 构造结构元素为正弦，对待分析原始信号进行自互补TopHat变换。由于形态学滤波所选结构元素的形状与待分析信号的形状越相近，滤波效果越好。发电机在定转子短路、气隙偏心故障下定子振动信号频率为50 Hz（电频率）整数倍的正弦波，所以构造正弦结构元素进行滤波处理，可获得最佳的滤波效果。

（2） 正弦结构元素的幅值及长度经嵌套遍历循环选取不同数值并与原始信号进行自互补TopHat变换，计算变换后信号中故障振动特征频率的能量与信号总能量的比值，选择遍历过程中能量比最大时所对应的幅值和长度作为正弦结构元素的最佳幅值及长度。

（3） 将待分析原始信号与最佳幅值及长度的正弦结构元素进行自互补TopHat变换，计算增强后信号的频谱，并与理论分析结果作对比，对发电机故障进行诊断与识别。

增强后频谱如图8所示。

图8增强后振动频谱

Fig.8Enhanced stator vibration spectra

观察图8（a）可知，2002年定子振动频谱中2倍频谱线突出，幅值为0.5914 mm/s。对比图8（b）可知，历经13年运行，发电机出现气隙静偏心故障，2倍频谱线幅值从0.5914 mm/s增加到了0.6985 mm/s，增幅为18.1%。复合故障1下2倍频振幅为0.8151 mm/s，相对静偏心增长了16.7%；4倍频振幅为0.1834 mm/s，6倍频振幅为0.0831 mm/s。复合故障2下2倍频振幅为1.0329 mm/s，相对复合故障1增长了26.7%；4倍频振幅为0.2271 mm/s，相对复合故障1增长了23.8%；6倍频振幅为0.0982 mm/s，相对复合而故障1增长了18.2%。复合故障3下2倍频振幅为1.1825 mm/s，相对静偏心相对复合故障1增长了45.1%；4倍频振幅为0.2504 mm/s，相对复合故障1增长了36.5%；6倍频振幅为0.1067 mm/s，相对复合故障1增长了27.2%。

综上可知， 理论解析推导、有限元仿真结果以及实验测试数据相互吻合。

4结论

本文对气隙静偏心和定子短路故障的相对位置对定子振动特性的影响进行解析分析、数值计算和实验研究，结果表明：

（1） 正常运行和气隙静偏心单故障下，发电机定子产生2倍频振动；气隙静偏心与定子匝间短路复合故障下，发电机定子产生2倍频、4倍频与6倍频振动。发电机分别处于正常、单故障以及复合故障下，定子振动会依次增强。

（2） 气隙静偏心与定子匝间短路复合故障下，同等故障程度时，发电机定子振动幅度与短路位置有关，短路位置越接近最小气隙处，各倍频振动幅度越大，越远离最小气隙处，各倍频振动幅度越小。

论文成果在现有研究基础上进一步完善了气隙静偏心与定子匝间短路故障的诊断判据。

参考文献：

[1]谭善军. 汽轮发电机偏心故障的交叉特征与诊断方法研究[J].中国电业（技术版）， 2012， （12）： 39—43.

TAN Shanjun. Research on steam turbine generator eccentric fault cross characteristics and diagnostic methods[J]. China Electric Power （Technology Edition）， 2012， （12）： 39—43.

[2]Blodt M， Regnier J， Faucher J. Distinguishing load torque oscillations and eccentricity faults in induction motors using stator current Wigner distributions [J]. IEEE Transactions on Industry Applications， 2009， 45（6）： 1991—2000.

[3]赵向阳， 葛文韬. 基于定子电流法监测无刷直流电动机转子动态偏心的故障模型仿真研究[J]. 中国电机工程学报， 2011， 31（36）： 124—130.

ZHAO Xiangyang，GE Wentao. Simulation research of fault model of detecting rotor dynamic eccentricity in brushless DC motor based on motor current signature analysis [J]. Proceedings of the CSEE， 2011， 31（36）： 124—130.

[4]万书亭， 何玉灵， 唐贵基， 等. 发电机气隙偏心时定子并联支路的环流特性分析[J].高电压技术， 2010， 36（6）： 1547—1553.

WAN Shuting， HE Yuling， TANG Guiji， et al. Analysis on stator circulating current characteristics under eccentricity faults of turbogenerator[J]. High Voltage Engineering， 2010， 36（6）： 1547—1553.

[5]Jian Li，Yunhyun Cho. Dynamic reduction of unbalanced magnetic force and vibration in switched reluctance motor by the parallel paths in windings [J]. Mathematics & Computers in Simulation， 2010， 81（2）： 407—419.

[6]Prasad B J C， Sanker Ram B V. Interturn fault analysis of synchronous generator using finite element method （FEM） [J]. International Journal of Recent Technology and Engineering， 2013， 2（5）： 150—156.

[7]Sarikhani A， Mohammed O A. Interturn fault detection in PM synchronous machines by physicsbased back electromotive force estimation [J]. IEEE Transactions on Industrial Electronics， 2013， 60（8）： 3472—3484.

[8]何玉灵，万书亭，唐贵基，等. 定子匝间短路对发电机并联支路环流特性的影响[J].电机与控制学报， 2013， 17（3）：1—7.

HE Yuling，WAN Shuting，TANG Guiji， et al. Effects of stator interturn short circuit on the circulating current inside the parallel branch loop[J]. Electric Machines and Control， 2013， 17（3）： 1—7

[9]孙宇光，余锡文，魏锟，等. 发电机绕组匝间故障检测的新型探测线圈[J]. 中国电机工程学报， 2014， 34（6）： 917—924.

SUN Yuguang， YU Xiwen， WEI Kun， et al. A New type of search coil for detecting interturn faults in synchronous machines [J]. Proceedings of the CSEE， 2014，34（6）： 917—924.

[10]唐贵基， 何玉灵， 万书亭， 等. 气隙静态偏心与定子短路复合故障对发电机定子振动特性的影响[J].振动工程学报， 2014， 27（1）： 118—127.

TANG Guiji， HE Yuling， WAN Shuting， et al. Effect of static eccentricity & stator short circuit composite faults on stator vibration characteristics of generator [J]. Journal of Vibration Engineering， 2014， 27（1）： 118—127.

[11]何玉灵，王发林，唐贵基，等. 考虑气隙偏心时发电机定子匝间短路位置对电磁转矩波动特性的影响[J].电工技术学报，2017，3（7）：11—19.

HE Yuling，WANG Falin，TANG Guiji，et al. Effect of stator interturn short circuit position on electromagnetic torque of generator with consideration of airgap eccentricity[J]. Transactions of China Electrotechnical Society， 2017，3（7）：11—19.

[12]何玉灵，蒙玉超，唐贵基，等.基于正弦结构元素的自适应 TopHat 变换及发电机特征振动信号增强检测[J].中国电机工程学报，2016，36（15）：4266—4273.

HE Yuling， MENG Yuchao， TANG Guiji， et al.SelfAdapted TopHat transformation based on sinestructure element and its application in enhanced characteristic vibration signal detection of generator[J].Proceedings of the CSEE，2016，36（15）：4266—4273.

Effect of stator interturn short circuit position on stator vibration of generatorHE Yuling， PENG Bo， WAN Shuting（Department of Mechanical Engineering， North China Electric Power University， Baoding 071003， China）Abstract： This paper analyzes the effect of the relative position of static airgap eccentricity and stator interturn short circuit on the stator vibration characteristic of generator via theoretical analysis， numerical simulation， and experimental study. Firstly， the detailed expressions of the stator magnetic pull per unit area with stator interturn short circuit location information are deduced， and the effect of short circuit position on magnetic pull is obtained. Then， the finite element model of example generator is set up to calculate the stator magnetic pull under normal condition， the static airgap eccentricity fault， and the composite fault （composed by static airgap eccentricity & stator interturn short circuit） with different shorted positions. Finally， the stator vibration signals of MJF306 type fault simulating generator at different stator short circuit positions are measured， which has the consistent result with the theoretical analysis and the numerical simulation. It is shown that， the stator vibration amplitude is associated with short circuit position when the generator under static airgap eccentricity & stator interturn short circuit composite fault. The shorted position is more near the min airgap position， the bigger the vibration amplitudes of each harmonic component. On the contrary， the shorted position is more far away the min airgap position， the smaller the vibration amplitudes of each harmonic component.Key words： fault diagnosis； turbo generator； stator vibration； static airgap eccentricity； stator interturn short circuit作者簡介： 何玉灵（1984—），男，博士，副教授。电话：（0312）7525043；Email：heyuling1@163.com

通讯作者： 万书亭（1970—），男，教授，博士生导师。电话：（0312）7525026；Email：13582996591@139.com