大跨度钢拱桥H型吊杆水平抗风索耦合系统扭转自振特性分析
2018-05-31汪志昊徐凯赵洋
汪志昊 徐凯 赵洋

摘要: 将水平抗风索对钢拱桥H型刚性吊杆的约束作用简化为水平弹簧的弹性支承作用,推导了一对水平抗风索的等效扭转弹簧弹性支承刚度计算公式,基于建立的H型吊杆水平抗风索耦合系统扭转振动理论模型,相应提出了耦合系统扭转自振特性求解理论方法,并通过有限元法验证了该方法的准确性;分析了抗风索位置、刚度参数对H型吊杆扭转自振特性的影响规律,据此提出了水平抗风索对H型吊杆第1阶扭转模态振动控制的参数设计方法。研究表明:抗风索安装位置不同,其等效扭转刚度对耦合系统扭转自振特性的影响程度也不同,且抗风索位置决定了耦合系统扭转自振频率增长极限值;抗风索等效扭转刚度决定了吊杆扭转振型结点个数;当仅考虑H型吊杆第1阶扭转振动模态控制时,宜将抗风索设置在吊杆中心位置处,此时随着抗风索等效扭转刚度的逐渐增大,吊杆第1阶扭转自振频率将超越第2阶,相应扭转振型在抗风索位置处的振型节点坐标逐渐趋于0,即吊杆变为几乎完全独立的两段。该文研究成果可为H型吊杆的水平抗風索减振优化设计提供重要依据。关键词: 水平抗风索;钢拱桥; H型吊杆; 等效扭转刚度; 扭转自振特性
中图分类号: TU311.3; TU312+.1文献标志码: A文章编号: 10044523(2017)04062010
DOI:10.16385/j.cnki.issn.10044523.2017.04.013
引言
制作和养护方便的H型刚性吊杆,在钢拱桥中应用较为普遍。然而,这种具有钝体截面形式的开口薄壁钢结构杆件,长细比大,阻尼小,且扭转基频偏低,在风荷载下易发生风致扭转颤振等多种有害振动,严重影响桥梁正常运营甚至危及桥梁整体安全[12]。工程界常采用调谐质量阻尼器[34]、气动措施[5]或水平抗风索[67]等方法抑制H型吊杆的风致振动。其中水平抗风索减振措施,通过抗风索将各吊杆串联形成索杆耦合系统,使各吊杆运动相互牵连,增加吊杆整体刚度,提高吊杆自振频率从而抑制吊杆振动。2006年中国某钢桁架拱桥遭遇台风袭击后,桥上多根H型吊杆发生强烈扭转振动,导致吊杆上下端翼缘板普遍破坏,最严重的几乎断裂,事后采用了水平抗风索减振抑振[6],国外也早有类似的应用实例[7]。虽然抗风索在H型吊杆振动控制已有应用,但相关理论研究偏少,已有抗风索减振主要集中于斜拉索的辅助索[89]减振领域。据目前所调研的公开发表文献所示,未发现有关H型吊杆水平抗风索(简称:抗风索)耦合系统自振特性的解析或半解析方法,且相应的抗风索参数优化设计方法也尚未建立。
本文提出了求解H型吊杆水平抗风索耦合系统扭转自振特性的理论方法,结合所建立的H型吊杆水平抗风索耦合系统扭转振动理论模型和提出的抗风索位置处吊杆扭转振动相容连续性条件,可求解耦合系统扭转自振频率和吊杆扭转振型,通过与有限元结果对比验证了方法的准确性。此外,通过抗风索参数分析,明确了抗风索位置、刚度参数对H型吊杆扭转自振特性的影响规律,得到了抗风索对吊杆前2阶扭转振动模态的优化布置与刚度参数取值。最后,提出了抗风索对H型吊杆第1阶扭转振动模态控制的参数优化设计方法。
1H型吊杆抗风索耦合系统扭转振动理论模型〖*2〗1.1H型吊杆抗风索耦合系统为提高细长H型吊杆的自振频率,实桥工程一般采用1道水平抗风索串接多根吊杆,本文初步研究以风振问题尤其突出的最长吊杆与抗风索组成的耦合系统作为研究对象,分析抗风索对单根H型吊杆扭转自振特性的影响规律。H型吊杆与桥面及拱肋一般均采用高强螺栓连接,边界条件处于铰接和固结之间,与固结更为接近。为简化计算,将H型刚性吊杆简化为受轴向拉力的两端固结梁,水平抗风索对吊杆的扭转刚度贡献简化为一对水平弹簧的等效扭转弹性支承作用,由此建立的H型吊杆水平抗风索耦合系统如图1所示,其中位于X1位置的一对水平抗风索采用水平弹簧弹性支承描述,相应4个弹簧弹性支承刚度记为k1,k2,k3,k4,由此组成的等效扭转弹簧记为S(图1虚线所示)。以弹性支承位置X1处为分割点,吊杆全长L被分为2段,长度分别记为L1和L2。各段吊杆扭转角位移用i(x,t)表示,其中Xi-1 图1H型吊杆水平抗风索耦合系统 Fig.1The coupled system with Hsection hangers and horizontal windresistant cables第4期汪志昊,等: 大跨度钢拱桥H型吊杆水平抗风索耦合系统扭转自振特性分析振 动 工 程 学 报第30卷1.2H型吊杆扭转振动微分方程 H型吊杆属开口薄壁杆件,根据符拉索夫开口薄壁约束扭转理论[10],取图1中x方向H型吊杆微元段dx,其扭转受力[1112]如图2所示: 图2H型吊杆微元扭转受力 Fig.2Torsional force in the microunit of a Hsection hangerT=Ts+Tω Ts=-GJi(x,t)x Tω=E′Cω3i(x,t)x3 TP=-PIPAi(x,t)x fI=-ρIP2i(x,t)t2(1)式中T,Ts,Tω,TP与fI分别为截面总扭矩、自由扭转扭矩、约束扭转扭矩、轴向力产生的扭转方向的扭矩与截面扭转惯性力;G为剪切弹性模量;J=∑13bs3[13]为自由扭转惯性矩,b和s分别为截面线段长度、宽度;E′=E1-μ2[10]为H型吊杆折算弹性模量,E和μ分别为杨氏弹性模量、材料泊松比;Cω=32t124[14]为翘曲扭转常数,和参数与图1相同;P为轴向力(拉力为正);IP为吊杆极惯性矩;A为吊杆截面面积;ρ为吊杆材料密度。 通过图2吊杆扭转受力分析,可得吊杆微元扭转平衡方程Tω+Tωx+Ts+Tsx+TP+TPx-
Ts-Tω-TP=fI(2)将式(1)代入式(2)可得各段吊杆扭转振动微分方程E′Cω 4i (x,t)x4i -(GJ + PIP A)2i (x,t)x2i =
-ρIP 2i (x,t)t2(3)式中E′Cω表示约束扭转刚度,GJ为自由扭转刚度,t为时间。
1.3水平抗风索等效扭转弹簧刚度
图3给出H型吊杆在抗风索位置处的横截面受力。由图可知,可将同一截面处4个水平弹簧等效为单个扭转弹簧。令S为一对水平抗风索的等效扭转弹簧刚度,扭转角记为θ。H型吊杆受到抗风索的弹性支承作用力为:F1=F3=kδx3
F2=F4=kδx1(4)式中k=2E1A1l为单侧水平抗风索弹性支承刚度,E1,A1与l分别为抗风索材料杨氏弹性模量、抗风索截面面积和抗风索长度;δx1,δx2与δx3为吊杆在抗风索弹性支承方向位移,有δx1=δx3=δx2,且δx2=2sinθ。
图3H型吊杆横截面受力
Fig.3Crosssectional torsional force of a Hsection hanger
则H型吊杆在抗风索位置处受到弹性支承作用的等效扭转弹簧平衡方程为Sθ=(F1+F3)=(F2+F4)=2kδx2(5)θ较小时,有θ≈sinθ,式(5)化简可得抗风索等效扭转弹簧刚度S=2E12A1l(6)1.4H型吊杆扭转模态自振频率与振型求解
由结构动力学分离变量法,吊杆扭转角位移i(x,t)可以表示为n,i(x,t)=θn,i(x)ejωnt(7)式中n为吊杆扭转振动阶次(n=1,2,3,…);j=-1为虚数单位;n,i(x,t)和θn,i(x)分别为第i段吊杆的第n阶扭转振动角位移和转角模态位移函数(i=1,2);ωn为H型吊杆水平抗风索耦合系统第n阶扭转自振圆频率。将式(7)代入式(3)可得θn,i(x)=An,isin(cLi)+Bn,icos(cLi)+
Cn,isinh(dLi)+Dn,icosh(dLi)(8)式中c=[(a4+g44)12-g22]12,d=[(a4+g44)12+g22]12,a4=ω2ρIPE′Cω,g2=GJ+PIPA-1E′Cω。An,i,Bn,i,Cn,i和Dn,i为第i段吊杆的第n阶扭转振型实常数。
令θn(x)为整段吊杆第n阶转角模态位移函数,有θn(x)=θn,1(x)·(x≤X1)+
θn,2(x)·(x>X1)(9)参考中间弹性支承连续梁弯曲振动存在的位移、转角等相容连续性条件[15],提出H型吊杆在抗风索位置X1处的扭转振动相容连续性条件分别为:扭转角,扭转角变化率,双力矩与总扭矩,相应表达式分别为:n,1(XD1,t)=n,2(XU1,t)(10)
′n,1 (XD1,t) = ′n,2 (XU1,t)(11)
E′Cω ″n,1 (XD1,t) = E′Cω ″n,2 (XU1,t)(12)
E′Cω n,1 (XD1,t)-(GJ + PIP A) ′n,1 (XD1,t) =
Sn,2 (XU1,t) + E′Cω n,2 (XU1,t)-
(GJ + PIP A) ′n,2 (XU1,t)(13)式中 ′n,i(x,t),″n,i(x,t)与n,i(x,t)分别表示n,i(x,t)对x的第1阶、第2阶与第3阶导数;XU1和XD1分别表示吊杆在抗风索位置处的上、下侧截面。
将式(7)代入式(10)~(13)定义的扭转振动相容连续性条件,化简得到:θn,1 (L1 ) = θn,2 (0)
θ′n,1 (L1 ) = θ′n,2 (0)
θ″n,1 (L1 ) = θ″n,2 (0)(14)
E′Cω θn,1 (L1 )-(GJ + PIP A)θ′n,1 (L1 ) =
Sθn,2 (0) + E′Cω θn,2 (0)-(GJ + PIP A)θ′n,2 (0) 吊杆两端固结边界条件,扭转角n,i(x,t)与扭转角变化率 ′n,i (x,t)皆为0[11],相应表达式为:x=0 n,1 (0,t)=0→θn,1 (0)=0
′n,1 (0,t)=0→θ′n,1 (0)=0
x=L2 n,2 (L2 ,t)=0→θn,2 (L2 )=0
′n,2 (L2 ,t)=0→θ′n,2 (L2 )=0(15)将式(8)代入式(15)可得:Bn,1+Dn,1=0Dn,1=-Bn,1
cAn,1+dCn,1=0Cn,1=-cdAn,1
An,2sin(cL2)+Bn,2cos(cL2)+
Cn,2sinh(dL2)+Dn,2cosh(dL2)=0
An,2ccos(cL2)-Bn,2csin(cL2)+
Cn,2dcosh(dL2)+Dn,2dsinh(dL2)=0(16)式(18)代入式(14),并與式(16)联立写为矩阵形式RΦ=0(17)式中R为系数矩阵,
R=R11R12
R21R22,R11=0101
cd010
0000
0000,R12=0000
0000
sin(cl2)cos(cl2)sinh(dl2)cosh(dl2)
ccos(cl2)-csin(cl2)dcosh(dl2)dsinh(dl2),R21=sin(cl1)cos(cl1)sinh(dl1)cosh(dl1)
ccos(cl1)-csin(cl1)dcosh(dl1)dsinh(dl1)
-c2sin(cl1)-c2cos(cl1)d2sinh(dl1)d2cosh(dl1)
-(αc3+βc)cos(cl1)(αc3+βc)sin(cl1)(αd3-βd)cosh(dl1)(αd3-βd)sinh(dl1),R22=0101
c0d0
0-c20d2
(αc3+βc)ε(βd-αd3)ε。其中,α=E′CωLGJ,β=(1+PIPGJ)L;ε=SLGJ为抗风索等效扭转弹簧无量纲刚度;Φ为待定参数向量,表示为Φ=[An,1 Bn,1 Cn,1 Dn,1 An,2 Bn,2 Cn,2 Dn,2]T式(17)若存在Φ≠0,则需满足detR=0(18)式(18)中仅有ωn一个未知量,通过MATLAB软件利用弦截法进行数值计算可得到H型吊杆抗风索耦合系统各阶扭转自振圆频率ωn的数值,将ωn代回式(17)中可得Φ,再将Φ带入式(8)即可得到各段吊杆扭转振型,求解全过程如图4所示。
图4H型吊杆抗风索耦合系统扭转自振特性求解流程图
Fig.4The calculation flowchart to solve the torsional dynamic characteristics of coupled system with Hsection hanger and windresistant cables
图5H型吊杆横截面尺寸(单位:mm)
Fig.5Crosssectional dimension of a Hsection hanger(Unit:mm)
2有限元分析与验证〖*2〗2.1H型吊杆与抗风索基本参数某大跨度钢桁架拱桥H型吊杆原型截面如图5所示,基本参数如表1所示。水平抗风索采用fpk=1860 MPa,7s15.2 mm规格钢绞线,弹性模量E1=1.95×105 MPa,泊松比γ=0.3,密度ρ1=8600 kg/m3。由于抗风索(钢绞线)初张力对吊杆动力特性影响极小[16],本文暂时忽略初张力影响,张拉应力统一取为0.75fpk。
2.2H型吊杆抗风索耦合系统有限元模型
吊杆壁厚与特征尺寸比值很小,有限元模型(图6)采用SHELL63壳单元;为模拟吊杆轴力,吊杆边界条件处理为高强螺栓区一端固结,另一端释放轴向自由度并施加轴向荷载模拟轴力几何刚度对扭转自振频率的影响。抗风索采用LINK10杆单元模拟,通过设置初应变实常数模拟抗风索初张力,锚固端边界条件设为固结。实桥工程抗风索与吊杆一般采用索卡连接,有限元建模忽略两者的接触摩擦作用,以共节点方式处理。
表1H型吊杆基本参数
Tab.1Basic parameters of a Hsection hanger
截面几何参数取值吊杆参数/m0.5吊杆参数/m1.182吊杆长度L /m40.212截面面积A /m22.964×10-2惯性矩IZ /m43.751×10-4惯性矩IY /m47.602×10-3极惯性矩IP/m47.977×10-3自由扭转惯性矩J/m42.8065×10-6翘曲常数Cω/m6 1.310×10-4杨氏弹性模量E /(N·m-2)2.0×1011剪切弹性模量G/(N·m-2)7.692×1010材料密度ρ/(kg·m-3)7850轴向拉力(拉为正)P/kN 2107图6H型吊杆抗风索耦合系统有限元模型
Fig.6Finite element model of the coupled system with a Hsection hanger and windresistant cables2.3H型吊杆扭转模态自振频率与振型验证
由公式(6)可知,抗风索等效扭转弹簧刚度与抗风索长度、弹性模量和截面面积相关,其中较为容易改变的是抗风索长度和截面面积。分别改变抗风索长度和截面面积使得抗风索等效扭转弹簧无量纲刚度ε变化,其中截面面积通过改变抗风索根数实现。
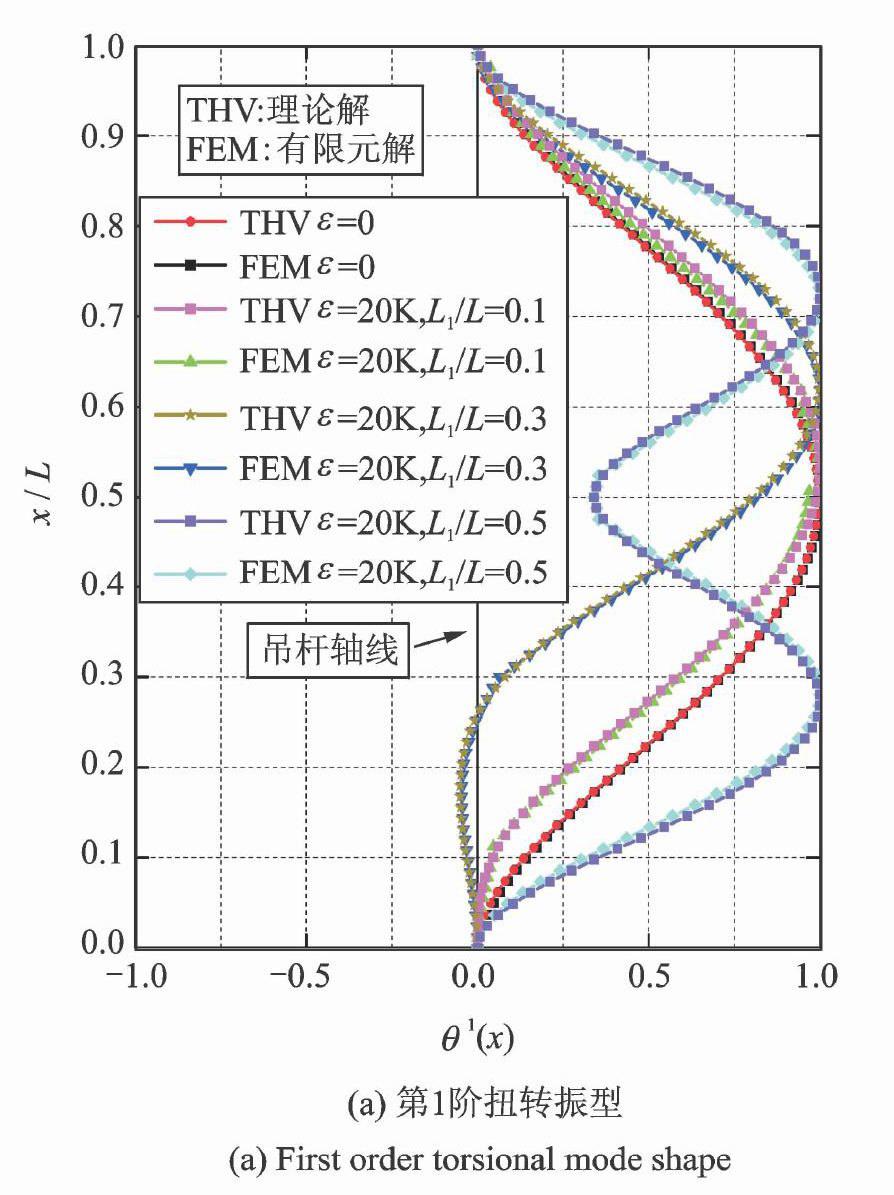
取长度l=100 m,截面面积A1=27.8 mm2(0.25根前述钢绞线)对应的抗风索等效扭转弹簧无量纲刚度K=35作为ε的基准值,分别取ε=0及ε=20K时不同抗风索安装位置L1/L=0.1,0.3,0.5的情况,计算并比较各工况下H型吊杆扭转自振频率和振型的理论解与有限元结果。吊杆前2阶扭转自振频率如表2所示,对应的各阶扭转振型如图7所示。
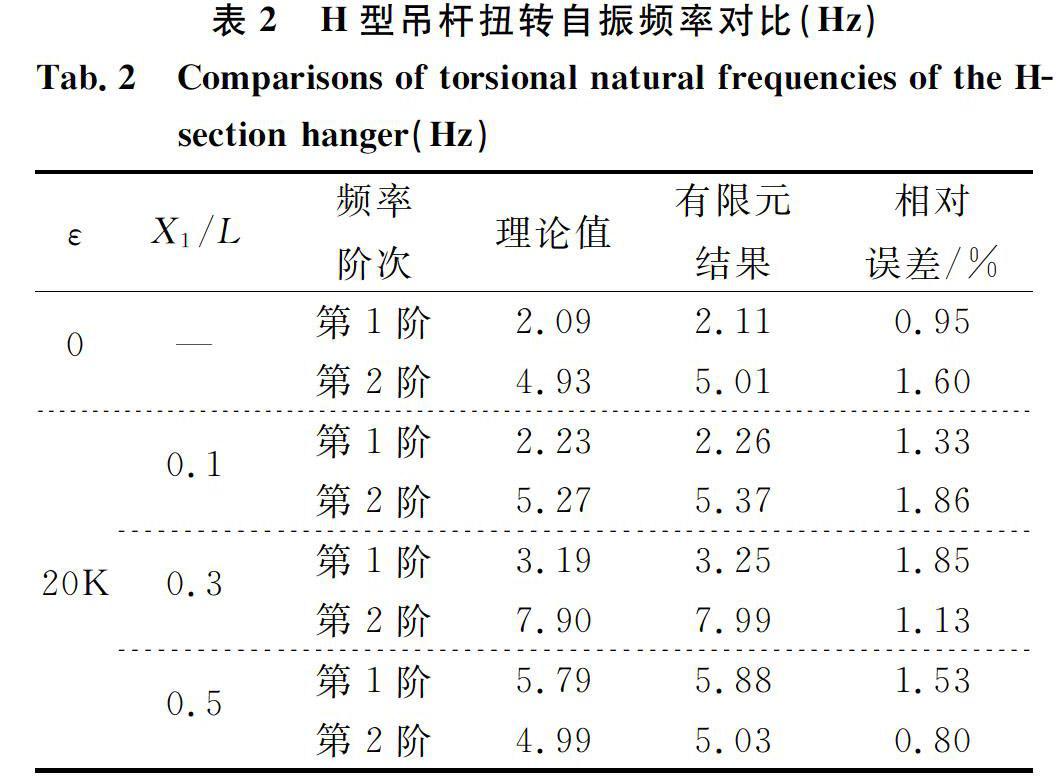
表2H型吊杆扭转自振频率对比(Hz)
Tab.2Comparisons of torsional natural frequencies of the Hsection hanger(Hz)
εX1/L频率
阶次理论值有限元
结果相对
误差/%0—第1阶2.092.110.95第2阶4.935.011.600.1第1阶2.232.261.33第2阶5.275.371.8620K0.3第1阶3.193.251.85第2階7.907.991.130.5第1阶5.795.881.53第2阶4.995.030.80
图7吊杆第1,2阶扭转振型对比
Fig.7Comparisons of firsttwo order mode shapes between theoretical values and finite element method
值得注意的是,若抗风索等效扭转弹簧无量纲刚度ε为0,则H型吊杆抗风索耦合系统退化为普通吊杆。由式(18)可得2cd([1-cos2cLcosh2dL]+
(d2-c2)sin2cLsinh2dL=0(19)公式(19)与文献[17]结果完全一致。同时,由表2可知,各工况下对比发现H型吊杆前2阶扭转自振频率理论值与有限元结果吻合良好,误差均不超过2%。由图7可见,吊杆第1和2阶扭转振型的理论解与有限元结果也高度吻合。可见,本文理论方法对求解H型吊杆抗风索耦合系统扭转自振频率与吊杆扭转振型具有较高的精度。因此,后文均基于本节H型吊杆及抗风索参数信息,采用提出的H型吊杆抗风索耦合系统扭转自振特性求解理论方法进行抗风索参数分析。
3抗风索位置、刚度参数对H型吊杆扭转自振特性影响规律3.1扭转自振频率
分析了抗风索位置、刚度参数对H型吊杆扭转自振频率的影响规律。前2阶吊杆扭转自振频率理论值与有限元计算结果见图7,不同抗风索扭转刚度下吊杆扭转自振频率最大值见表3,其中fn为H型吊杆第n阶扭转振动工程自振频率,有fn=ωn/(2π),据此可得如下规律:
(1)图8(a)可知:同一抗风索位置处,随着抗风索等效扭转弹簧无量纲刚度ε的增大,第1阶扭转自振频率均随之增大;ε不变时,抗风索安装位置越靠近吊杆端部,扭转基频变化越小,越靠近吊杆中点,其扭转基频增幅越大,存在较为明显的分区现象,在0.45≤L1/L≤0.55且ε≥10K时,吊杆扭转基频曲线斜率变化较大,且各曲线在L1/L=0.5处取得极值;在ε增大至一定值时(ε≥50K),同一抗风索安装位置处,吊杆扭转基频变化极小,并逐渐趋于稳定极限值fu1(ε=50K,500K时两曲线近乎重合)。
(2)由图8(b)可知:随着ε的增大,吊杆第2阶扭转自振频率随之增大,并逐渐趋于极限值fu2,扭转自振频率变化曲线关于L1/L=0.5对称;不同ε下,吊杆第2阶扭转自振频率取得极值时的抗风索位置(L1/L)不同,ε=K→500K时,各曲线极值对应的横坐标在L1/L=(0.3→0.35)或(0.7→0.65)两区间内,并不同于第1阶扭转自振频率只存在一个极值横坐标(L1/L=0.5);抗风索位于吊杆振型结点处对扭转自振频率无影响(L1/L=0.5时第2阶扭转自振频率保持不变)。
(3)考虑到实际工程中控制第1阶扭转振动模态,宜将抗风索设置在吊杆中心位置处;对第2阶扭转振动模态的控制,宜采用较大的抗风索扭转刚度,且其安装位置建议设置在吊杆长度的0.35或0.65处。
(4)由表3可见,吊杆第1阶扭转自振频率最大可提高为原值的3.10倍(ε=500K,L1/L=0.5);第2阶扭转自振频率最大可提高为原值的1.80倍(ε=50K,500K,L1/L=0.35,0.65),扭转自振频率大幅增加。
图8抗风索不同位置时吊杆第1,2阶扭转自振频率随ε的变化规律
Fig.8First and second order torsional natural frequencies of the hanger connected by the windresistant cables with different locations versus ε
表3吊杆前2阶扭转自振频率最大值(Hz)
Tab.3The maximum natural frequencies of the first two order torsional mode of the hanger(Hz)
εf1 f202.09 4.93 K(1.41×103)2.97 5.39 5K(7.05×103)4.49 6.87 10K(1.41×104)5.28 7.54 20K(2.82×104)5.798.7450K(7.05×104)6.34 8.86 500K(7.05×105)6.488.86自振頻率极限提高百分比
(ε=500K) 210.05% 79.66%3.2扭转振型
由3.1节可知,抗风索位于吊杆中心位置处对1阶扭转自振频率提高最大,当L1/L=0.35或0.65且ε>5 K时对2阶扭转自振频率提高最大。因此,特别针对L1/L=0.5,0.35时2个特殊位置,研究吊杆前2阶扭转振型随抗风索等效扭转弹簧无量纲刚度ε的变化规律(图9,10),可见:
(1)对吊杆第1阶扭转振型,当L1/L=0.5且等效扭转刚度较小时(ε=0,K),第1阶扭转振型表现为振型幅值最大值在0.5L,随着ε的增大,第1阶扭转振型在0.5L处的振型节点坐标逐渐趋于0,此时出现了2个振型幅值位置,分别在0.25L和0.75L处;当L1/L=0.35时,随着ε的增大,振型幅值出现反相位,且在抗风索位置L1/L=0.35处扭转角位移逐渐变为0。ε越大,抗风索对吊杆的约束作用越强,最终在此处趋于固结。
(2)对吊杆第2阶扭转振型,当L1/L=0.5时,第2阶扭转振型随着ε的增大并无变化,这与3.1节图7(b)中抗风索位于吊杆中心位置处的第2阶扭转自振频率保持不变相一致;当L1/L=0.35,随着ε的增大(ε=20 K,50 K,500 K),第2阶扭转振型与吊杆轴线有两个交点。
(3)在ε达到一定数值时,吊杆前2阶扭转振型均会由于抗风索过强的扭转约束作用而在此处趋于固结,扭转角位移为0,此时吊杆被完全分为2段。
图9H型吊杆第1阶扭转振型图
Fig.9Firstorder torsional mode shapes of the Hsection hanger图10H型吊杆第2阶扭转振型图
Fig.10Secondorder torsional mode shapes of the Hsection hanger
4水平抗风索对H型吊杆扭转模态减振参数设计由3.1小节可知,对工程中优先控制的吊杆第1阶扭转振动模态,宜将抗风索设置在吊杆中心位置处,此时扭转基频增幅可达到最优值。因此,可固定该最优抗风索位置,研究吊杆第1和2阶扭转自振频率的相关关系。吊杆前2阶扭转自振频率随ε变化规律如图11所示,可得如下规律:
(1)随着抗风索等效扭转弹簧无量纲刚度ε的增大,吊杆第1阶扭转自振频率(f1)开始增长较快、增幅较大,后期逐渐变缓并进入平台期,频率趋于稳定;由于抗风索安装位置在吊杆中点位置处,第2阶扭转自振频率保持定值并无变化,即为无抗风索时的吊杆第2阶扭转自振频率(f2)。
(2)观察吊杆第1,2阶扭转自振频率曲线,随着ε的增大,第1阶扭转自振频率在a点后超越了第2阶,此时虽然第1阶扭转自振频率在a点之后仍随抗风索扭转刚度的增大继续增加,但第2阶扭转自振频率先于第1阶出现,改变了吊杆首次出现的扭转自振频率阶次。
(3)第1阶扭转自振频率在ε大于某一阙值时不再变化,达到极限值fu1,即为1/2吊杆长度的第1阶扭转自振频率,此时吊杆在抗风索位置处趋于固结,吊杆被分为完全独立且长度相等的两段,整段吊杆的第1阶扭转自振频率即为各段吊杆扭转基频。
由于在a点后第2阶扭转自振频率先于第1阶出现(见图11)。因此,对于优先控制第1阶扭转振动模态来说,可将a点对应的扭转自振频率作为吊杆的扭转目标频率,对应的抗风索扭转刚度作为目标刚度。同时,实桥抗风索一般锚固于主拱肋或与相邻吊杆串联,其安装位置决定了抗风索长度基本为定值。从而可根据公式(6)反算抗风索截面面积,确定抗风索参数取值A1-aim=Saimlaim2E12(20)式中A1-aim为所需抗风索截面面积;Saim为抗风索扭转目标刚度,即a点(图11)对应横坐标;laim为对应的抗风索长度。
图11吊杆抗风索(吊杆中心位置)耦合系统扭转自振频率随ε的变化
Fig.11Natural frequencies of the coupled system with a hanger and midpoint windresistant cables versus ε5结论
(1)建立了H型吊杆水平抗风索耦合系统扭转振动理论模型,推导了抗风索等效扭转弹簧刚度计算公式,提出了H型吊杆在抗风索位置处的扭转振动相容连续性条件(扭转角、扭转角变化率、双力矩和总扭矩),同时结合吊杆两端边界条件,推导了H型吊杆抗风索耦合系统扭转自振特性求解理论方法,并通过有限元法验证了其正确性。
(2)H型吊杆第1阶扭转自振频率随抗风索位置、刚度的变化存在分区现象:当抗风索安装位置靠近吊杆端部时,吊杆扭转自振频率变化很小,当抗风索安装位置L1/L=0.45~0.55且等效扭转弹簧刚度ε≥10K时,扭转基频变化较大,并于吊杆中心位置处达到极限值,该值为1/2吊杆长度的第1阶扭转自振频率。吊杆第2阶扭转自振频率取得极值时的抗风索位置存在特定区间:随着抗风索等效扭转弹簧刚度的增大(ε=K→500K),取得极值时的抗风索安装位置L1/L由0.3→0.35,0.7→0.65转移。本文算例H型吊杆第1阶扭转自振频率最大可提高为原值的3.10倍,第2阶扭转自振频率最大可提高为原值的1.80倍,扭转自振频率大幅增加。
(3)建立了H型吊杆第1阶扭转模态振动控制的水平抗风索布置位置与刚度参数设计方法,即以吊杆第1,2阶扭转自振频率曲线交点作为吊杆扭转目标频率可反算抗风索参数取值。
参考文献:
[1]Keller P, Higgins C, Lovejoy S C. Evaluation of torsional vibrations in steel truss bridge members [J]. Journal of Bridge EngineeringASCE, 2015, 20(9): 04014102.
[2]陈政清, 刘慕广, 刘光栋, 等. H型吊杆的大攻角风致振动和抗风设计[J]. 土木工程学报, 2010, 43(2): 1—11.
Chen Zhengqing, Liu Muguang, Liu Guangdong, et al. Windinduced vibration and windresistant design of HSection hangers under large attack angles [J]. China Civil Engineering Journal, 2010, 43(2): 1—11.
[3]王浩, 劉海红, 陶天友, 等. TMD对列车作用下大跨钢桁架拱桥的振动控制研究[J]. 振动工程学报, 2014, 27(3): 385—391.
Wang Hao, Liu Haihong, Tao Tianyou, et al. Vibration control of longspan steel truss bridge subjected to train loading using TMD [J]. Journal of Vibration Engineering, 2014, 27(3):385—391.
[4]雷旭, 牛华伟, 陈政清, 等. 大跨度钢拱桥吊杆减振的新型电涡流TMD开发与应用[J]. 中国公路学报, 2015, 28(4): 60—68, 85.
Lei Xu, Niu Huawei, Chen Zhengqing, et al. Development and application of a newtype eddy current TMD for vibration control of hangers of longspan steel arch bridge [J]. China Journal of Highway and Transport, 2015, 28(4): 60—68, 85.
[5]刘慕广, 陈政清. 不同截面参数H型吊杆的气动性能[J]. 工程力学, 2013, 30(5): 221—226.
Liu Muguang, Chen Zhengqing. Aerodynamic performance of HSection hangers with different sectional parameters [J]. Engineering Mechanics, 2013, 30(5): 221—226.
