载荷时变的双层隔振系统自适应滑模控制

崔明月 刘红钊 屈重年 孙棣华

摘要： 针对实际应用双层隔振系统载荷时变的特性，设计了基于正交函数近似法的自适应滑模控制器的振动控制策略。首先，将系统的参考坐标置于名义载荷下的静态位移处，同时考虑到弹簧刚度的非线性特性，建立系统的非线性模型。其次，将系统的不确定部分用两个未知时变函数来描述，应用一系列加权正交函数的和来近似未知函数，基于滑模控制理论设计自适应滑模控制律，结合Lyapunov直接法推导正交函数序列系数的自适应更新律，同时可以保证系统的稳定性。与传统PID控制的对比仿真与实验结果表明，提出的自适应滑模控制策略能够更好地克服载荷时变的影响，提高了系统的控制性能。关键词： 主动控制； 双层隔振系统； 正交函数近似法； 自适应滑模控制

中图分类号： O328； TP183文献标志码： A文章编号： 10044523（2017）04061010

DOI：10.16385/j.cnki.issn.10044523.2017.04.012

引言

双层隔振系统具有结构简单、易于实现的优点，在车辆工程、船舶工程、航空航天等领域有着广泛的应用。双层隔振装置能够显著降低机械设备振动向外界的传递，是隔离振动和结构噪声的有效措施。然而，传统被动式的隔振方式对于低频振动，尤其是隔振装置自身固有频率附近的振动，难以进行有效隔离[1]。主动振动控制需外界供给能量，它是利用外界能量产生控制振动所需要的力。这种控制效果较好、原结构改变不大、调整方便。目前，在阻振、吸振和隔振领域，均已开展了相应的主动控制技术研究[13]。

杨铁军[3]等将CMAC神经网络与PID控制相结合设计了应用于双层隔振系统的复合控制器，实验结果表明适用于不同低频正弦激励信号下的振动控制。袁绍军、杨铁军[4]等针对常规模糊控制器量化因子难以自适应在线调整的问题，提出一种量化因子模糊自调整控制策略，应用于柴油机双层隔振系统控制，显著提高了隔振效果。C S Zhao[5]等将PID控制与模糊控制相结合应用于双层隔振系统控制。N Yagiz[6]针对七自由度汽车主动悬架的控制问题，运用反步控制策略设计了振动控制器。J M Rodriguez等[7]针对包含压电制动器的阻尼减振系统，基于微分平坦理论设计前馈控制律。然而，现有的振动主动控制方法通常只集中在削减有限模态的振动，并基于理想化的数学模型，在工程实际中的适用范围十分有限。随着现代控制技术的发展，自适应控制技术在主动振动控制中得到了越来越广泛的应用。在文献[1]中，研究者应用多点自适应有源控制策略应用于柴油机的双层隔振系统控制。文献[810]运用自适应控制理论进行主动控制研究，运用最小误差均方算法对系统误差通道进行在线辨识，取得了一定的控制效果。在文献[11]中，将自适应前馈补偿方法应用于机械耦合系统的振动控制，效果明显。遗憾的是，上述研究成果大都是以线性定常系统模型为基础，且没有考虑隔振系统载荷与参数的时变，这与工程实际中的系统特性并不相符。

第4期崔明月，等： 载荷时变的双层隔振系统自适应滑模控制振 动 工 程 学 报第30卷由于滑模控制器具有鲁棒性强、可靠性高与结构简单的优点，已在主动隔振系统中得到广泛应用。曾强洪等[12]提出应用滑模变结构控制实现隔振系统和混沌系统投影同步的新方法，在保持原有隔振系统隔振性能的前提下有效地消除了线谱。刘延斌等[13]基于系统的动力学模型，综合运用反演控制设计方法、自适应以及滑模控制技术，制定了系统的低频主动控制策略。在文献[14]中，针对带有电流变液智能阻尼器的半主动汽车悬架模型，运用滑模变结构方法设计了半主动悬架滑模控制器。在文献[15]中，设计了系统逆模型与滑模控制策略相结合的车辆悬架主动控制控制新方法。但是，上述研究都没考虑系统载荷时变的影响，并且所设计控制器不具有自适应性，这不利于其在实际工程中的应用。

鉴于此，针对实际工程中双层隔振系统载荷时变的特性，建立系统的非线性模型，提出一种正交函数近似方法与滑模控制相结合的复合自适应控制策略。运用正交函数近似方法对系统的不确定部分进行在线辨识，自适应滑模控制控制器在线产生控制力，并与常规PID控制算法进行对比仿真研究，结果表明基于正交函数近似法的自适应滑模控制策略在双层隔振系统主动控制中具有更好的减振效果。

1问题描述

利用柴油机作为初级振源，采用特殊中间质量形式加入作动器，构建双层隔振系统。图1为双层隔振系统结构示意图。m1（t）为时变的隔振对象—柴油机的质量，m2为中间质量块的质量，Fg为隔振对象工作时产生的竖直方向振动激扰力，Fk表示控制器产生的主动控制力。整个模型的控制原理是通过位移传感器测得m2的位移，送入控制器，然后通过控制器控制作动器A使其产生满足一定条件的主动作动力Fk来抵消m1的振动，从而达到隔振的目的。为使问题简化，在此仅考虑竖直方向的振动，将双层隔振系统简化为一个两自由度的弹簧阻尼质量系统。

图1隔振系统模型

Fig.1Model of vibration isolation system

柴油机工作时产生的振动主要是由机座向外传播，因此，只要根据中间质量的振动信号计算出使其振动趋于零所需要的施加到中间质量上的最优控制力Fk，则向机座传播的振动就趋于零，从而达到隔振的目的。

选取隔振对象m1（t）与中间塊质量m2坐标分别为x1和x2，对于上层弹簧，采用一个非线性弹簧，其弹簧力位移之间关系为Fk1=k11（x1-x2）+k12×（x1-x2）3。k11与k12分别为弹簧k1的线性与非线性弹性系数，x1-x2为弹簧发生弹性形变的位移。

由牛顿定律可得双层隔振系统的振动方程：m1（t）1+c1（t）（1-2）+k11（x1-x2）+

k12（x1-x2）3=Fg+Fk-m1（t）g

m22-c1（t）（1-2）+c22-k11（x1-x2）-

k12（x1-x2）3+k2x2=-Fk-m2g（1）式中k2为下层弹簧的弹性系数，c1（t）为时变的上层阻尼器的阻尼系数，c2为下层阻尼器的阻尼系数。

在实际应用中，被隔振对象的质量往往是变化的，所以考虑载荷的时变性更具有工程意义。假设被隔振对象的质量m1（t）有界，且其范围可以估计。那么，m1（t）可以表示为m1（t）=m1m+Δm1（t），m1m表示m1（t）的名义值，Δm1（t）为m1（t）的不确定部分，假设其有界。定义中间质量块m2的参考位置为x2r=（-m2-m1m）g/k2（g为重力加速度），是名义载荷m1mg与中间质量块重力m2g引起的弹簧k2的位移。

定义隔振对象m1（t）的参考位置为x1r=x2r+δ0，δ0<0为静态时弹簧变形。定义状态变量1=x1-x1r，2=x2-x2r，则式（1）可变为··1=1m1（t）[-k11（1-2）-k12[（1-2+

δ0）3-δ30]-c1（t）（·1-·2）-

Δm1（t）g+Fg+Fk]

··2=1m2[k11（1-2）+k12[（1-2+δ0）3-

δ30]+c1（t）（·1-·2）-c2·2-k22-Fk]（2）若取状态变量为x=12〖〗·1·2T，系统输出y=1，控制输入u=Fk，则振动方程（2）可写为：y…=f（x，t）+g（t）u

y=1（3）式中系统参数m1和c1是时变的，f（x，t）与g（t）是未知时变的函数，由式（2）与（3）可得f（x，t）与g（t）的表达式如下：f（x，t）=11（t）[-k11（1-2）-

k12[（1-2+δ0）3-δ30]-

c1（t）（·1-·2）-Δm1（t）g+Fg]+

1m1（t）[-k11（·1-·2）-k12[3（1-2+δ0）2·

（·1-·2）-δ30]-1（t）（·1-·2）-

c1（t）（··1-··2）-Δ1（t）g+g+k]

g（t）=11（t）-[m1（t）+m2]c1（t）m2m1（t）其中，f（x，t）表达式中的··1与··2由式（2）所决定。

由系统方程（3）可以看到，由于系统函数f（x，t）与g（t）是非线性函数，从控制角度看，系统输出y=1与控制输入u之间不满足齐次性与叠加性原理，是典型的严格非线性关系。再者，系统的两个状态1与2之间不是独立的，具有强耦合性，所以式（3）所描述的双层隔振系统是一个非线性、强耦合与多变量系统，常规线性控制器已不能满足其控制要求，这就要求设计一种鲁棒性强，且具有自适应能力的非线性控制器来克服系统函数时变的影响。同时，由于系统（3）中的函数f（x，t）和g（t）是时变未知的，不能直接利用式（3）进行控制器的设计。因此，必须对式（3）所映射的系统输出y与控制输入u之间的关系进行辨识。

2正交函数近似方法的隔振系统辨识

要进行控制器的设计，必须对双层隔振系统模型（3）中的未知函数f（x，t）与g（t）进行在线辨识。下面论述利用正交函数近似法对f（x，t）与g（t）進行在线辨识的方法。

正交实函数集合zi（t），i=1，2，…，n在区间t1，t2内满足以下条件∫t2t1zi（t）zj（t）dt=0，i=j

≠0，i≠j（4）进一步地，如果此函数集合满足∫t2t1z2idt=1，则称其为正则化函数集合。若定义在区间t1，t2内的实函数集合zi（t），i=1，2，…，n满足下式[16]∫t2t1ω（t）zi（t）zj（t）dt=0，i=j

≠0，i≠j（5）则zi（t），i=1，2，…，n在区间t1，t2内为相对于加权函数ω（t）的正交函数集合。如果ω（t）>0，将正交函数集合的每一项均乘上ω（t），则任何相对于加权函数ω（t）的正交函数集合均可转换为相对于1的正交函数集合。

任意函数h（t）在区间t1，t2内，可被无限级数的正交函数集合zi（t），i=1，2，…，n展开如下式h（t）=w1z1（t）+w2z2（t）+…+

wnzn（t）+…（6）此级数被称为广义Fourier级数，其系数称为h（t）相对于zi（t），i=1，2，…，n的Fourier系数。将h（t）乘以zn（t）并在区间t1，t2内积分，同时考虑zi（t）的正交性，可得∫t2t1h（t）zn（t）dt=wn∫t2t1z2n（t）dt（7）由上式可得系数wn为wn=∫t2t1h（t）zn（t）dt∫t2t1z2n（t）dt（8）由式（7）和（8）可以证明函数h（t）在区间t1，t2内满足如下关系[16]limn→∞∫t2t1h（t）-∑ni=1wizi2dt=0（9）由式（6）～（8），函数h（t）可表示为h（t）=∑ni=1wizi（t）+ε（t）（10）式中ε（t）=∑∞i=n+1wizi为近似误差。式（10）可表示为向量的形式h（t）=WTZ（t）+ε（t）（11）式中W=w1，w2，…，wnT为系数向量。假设选取的项数n足够多，ε（t）→0，则式（11）可近似表示为h（t）≈WTZ（t）（12）在工程实际中，通常选取Fourier级数作为正交函数，Fourier级数的定义如下：

一个定义在区间[t0，t0+T]内的函数h（t），若满足Dirichlet条件，则函数h（t）可展开为如下Fourier级数[17]：

h（t）=a0+∑∞n=1[ancos2nπt〖〗T+bnsin2nπtT]（13）

式中a0=1T∫t0+Tt0h（t）dt， an=2T∫t0+Tt0h（t）·cos2nπtTdt，bn=2T∫t0+Tt0h（t）sin2nπtTdt。

其中，a0，an，bn为Fourier系数。

在使用正交函数近似法设计自适应滑模控制器时，将利用式（12）来近似估计双层隔振系统（3）的不确定项f（x，t）与g（t），其中Z（t）为已知的时变向量，并结合未知常系数向量W来拟合未知函数。其中基底函数向量Z（t）选择Fourier级数，亦即Z（t）=[1， cosω1t， sinω1t， cosω2t， sinω2t，…，

cosωnf， sinωnft]T（14）式中ωi=2πi/T；i=1，2，…，nf；nf为基底函数向量的个数。

应用正交函数近似法可以将双层隔振系统（3）中未知的时变函数f（x，t）和g（t）表示成未知常数与已知Fourier级数的组合函数，进一步通过选择适当的Lyapunov函数，可以推导出未知常数的更新律，就能够达到运用函数近似法在线辨识的目的。

3自适应滑模控制律的设计3.1控制律的设计隔振系统的振动控制的目的是根据质量块的振动位移，计算出使其振动趋于零所需要的施加到质量块上的最优控制力Fk，使质量块的振动趋于零从而达到隔振的目的。

在控制系統中，利用滑模控制器在线计算控制力Fk。根据第2节中的研究结果，先利用正交函数近似法对双层隔振结构模型的时变未知函数进行辨识。基于函数近似法的自适应滑模控制系统结构如图2所示。该控制系统充分融合了滑模控制器鲁棒性强与正交函数近似法计算简单、实时性强的优点，达到对双层隔振系统实时控制的目的。

图2函数近似法辨识的自适应滑模控制系统

Fig.2Adaptive sliding mode control system based on function approximation method定义滑动面s=+λ1+λ2y（15）式中λ1>0与λ2>0是设计参数，决定被隔振对象位移量x1在滑动面上的收敛速率。上式对时间t求导得=y···+λ1+λ2（16）将式（3）代入式（16），得=f（x，t）+g（t）u+λ1+λ2=

g（t）[f（x，t）g-1（t）+u+

g-1（t）λ1+g-1（t）λ2]（17）采用指数趋近律=-λ3sgn（s）-λ4s（18）式中λ3>0，λ4>0为设计参数，sgn（s）为符号函数定义如下sgn（s）=-1，s<0

+1，s>0为使控制系统的输出收敛至滑动面，根据式（17）与式（18），可设计双层隔振系统的滑模控制律如下u=1g^（t）[-f^（x，t）-λ1-λ2-

λ3sgn（s）-λ4s]（19）式中f^（x，t）和g^（t）分别为f（x，t）和g（t）的估计值。

由式（19）可知，当g^（t）接近于零时，控制量u会趋于无穷大，所以g^（t）必须有一个最小值的限制，假设g（t）>g>0，g为g（t）下限值。

令fa=f（x，t）g-1（t），将式（19）代入式（17），得

=g（t）[（fa-f^a）+λ1（g-1-g^-1）+

λ2（g-1-g^-1）-λ3g^-1sgn（s）-λ4g^-1s]（20）

式中g-1=1/g（t），f^a为fa的估计值。上式中函数fa，f^a，g-1及g^-1均假设为有界的未知连续函数且满足Dirichlet条件，这些函数可应用函数近似法表示如下：fa=WTfaZfa

f^a=TfaZfa

g-1=WTgZg

g^-1=TgZg（21）式中Wfa，W^fa，Wg，W^g∈Rn为时变系数向量，而Zfa，Zg∈Rn是基底Fourier函数向量。因此，式（20）可写为=g（t）[TfaZfa+λ1TgZg+λ2TgZg-

λ3W^TgZgsgn（s）-λ4W^TgZgs]（22）式中Tfa=WTfa-W^Tfa

Tg=WTg-W^Tg（23）3.2 系统的自适应律设计

为证明双层隔振控制系统的稳定性及求得W^fa与W^g的更新律，选取如下的Lyapunov函数V（s，fa，g）=12s2+12g（t）（TfaQfafa+

TgQgg）（24）式中Qfa，Qg∈Rn×n为正定矩阵。

假设控制量增益g（t）是一个变化缓慢的函数，即（t）≈0。将式（24）所示的Lyapunov函数对时间t求导，得（s，fa，g）=s+g（t）（TfaQfa·fa+

TgQg·g）（25）因为Wfa及Wg为未知的常系数向量，由式（23）可知·Tfa=-W^·Tfa

·Tg=-W^·Tg（26）将式（22）与（26）代入式（25）可得（s，fa，g）=g（t）[TfaZfa+λ1TgZg+λ2TgZg-λ3W^TgZgsgn（s）-λ4W^TgZgs]s-g（t）（TfaQfaW^·fa+

TgQgW^·g）=g（t）{[TfaZfa+λ1TgZg+λ2TgZg-λ1W^TgZgsgn（s）-λ2W^TgZgs]s-TfaQfaW^·fa-

TgQgW^·g}=g（t）{Tfa（Zfas-QfaW^·fa）+Tg[Zgs（λ1+λ2）-QgW^·g]-W^TgZg（λ3s+λ4s2）}=

g（t）{Tfa（Zfas-QfaW^·fa）+Tg[Zgs（λ1+λ2）-QgW^·g]-（WTg-Tg）Zg（λ3s+λ4s2）}=

g（t）{Tfa（Zfas-QfaW^·fa）+Tg[Zg（λ1s+λ2s+λ3s+λ4s2）-QgW^·g]-WTgZg（λ3s+λ4s2）}（27）根据式（27），可选择W^fa与W^g的更新律如下：fa= Qf-1aZfas（28）

W^·g=Q-1gZg（λs+λ1|s|+λ2s2），（t）>g>0

Q-1gZg（λ1s+λ2s+λ3|s|+λ4s2，

0>（t）≤g & λ1s+λ2s+

λ3|s|+λ4s2<0

0，0<（t）≤g & λ1s+λ2s+

λ3|s|+λ4s2≥0（29）在式（29）中，W^fa更新律的设计是为了确保g（t）的估计值g^（t）满足g^（t）>g>0（g为g（t）的下界值）。如果选择适当的g，可保证式（19）中的控制量u趋于无穷大的情况不会发生。式（21）中各时变系数向量Wfa，W^fa，Wg，W^g可由式（28）与（29）来确定。

综上所述，所设计自适应滑模控制器工作过程为：

步骤1：由实际检测到的双层隔振系统的被隔振对象的振幅y=x1-x1r，根据式（15）计算滑动面函数s；

步骤2：由式（21），（28），29）来计算系统函数的估计值g^（t）和f^（x，t）；

步骤3：由滑模控制律（36）计算出作用于中间质量上的最优控制力：u=Fk。

3.3控制系统的稳定性分析

定理：双层隔振系统模型（3）在滑模控制律（19）及自适应律（28）和（29）的作用下，隔振对象的竖直方向位移y=1收敛到零。

证明：将式（28）和（29）代入式（27）可得（s，fa，g）=-g（t）WTgZg（λ3s+λ4s2）=

-g（t）g-1（t）（λ3s+λ4s2）=

-（λ3s+λ4s2）≤0（30）Lyapunov函数V（s，fa，g）是一个关于时间t的单调非增函数，所以V（s，fa，g）≤V（0）<∞，由式（25）可知s∈L∞，fa∈L∞，g∈L∞。因为

（s，fa，g）=-（λ3s+λ4s2）≤-λ4s2（31）

根据定积分性质，不等式两边同时积分，得∫∞0s2dt≤-1λ4∫∞0（s，fa，g）dt=

1λ4（V（0-V（∞））<∞（32）故s∈L2，所以s∈L2∩L∞。再者，由式（22）可知∈L∞，由Barbalat引理[18]，可知当t→∞时，有s→0。由式（15）可知，當t→∞时，有+λ1+λ2y=0（33）此时有y=c1exp（-λ1+λ21-4λ22t）+

c2exp（-λ1-λ21-4λ22t）（34）式中c1与c2是由y的初始值所决定的常数。由上式可知，当设计参数满足λ21-4λ2>0时，当t→∞时，y→0，即双层隔振系统的隔振对象的竖直方向位移1→0。

在实际应用中，为削弱抖振，用饱和函数sat（s，δ）代替符号函数sgn（s），饱和函数定义如下sat（s，δ）=-1，s<-δ

sδ，-δ≤s<δ

1，s≥δ（35）式中δ为饱和函数边界层厚度。双层隔振系统的滑模控制律（19）就变为u=1g^（t）[-f^（x，t）-λ1-λ2-

λ3sat（s，δ）-λ4s]（36）4数值仿真

为了验证所设计的双层隔振系统主动控制方法的有效性，在相同的条件下对设计的基于函数近似法的自适应滑模控制（ASMC， Adaptive Sliding Mode Control）算法与常规PID控制算法进行对比仿真。仿真所选取的系统参数如表1所示。经反复试验，ASMC控制器参数选择如下：λ1=2.1，λ2=1.0，λ3=λ4=1.2，饱和函数边界层厚度δ=0.06。反复试验后选择一组最佳的PID控制参数：比例系数kp=1.4，积分系数ki=0.2，微分系数kd=0.06。正交函数的基函数项数选取对系统模型中的系统函数f（x，t）与g（t）的辨识精度会产生重要的影响，如果正交函数的基函数的项数选的太少，运算速度快，但辨识精度低；反之，如果项数选的多，辨识精度高，但是运算速度慢，导致控制的实时性降低。

表1系统参数

Tab.1System parameters名称符号标称值上层质量块m1（t）/kg50+9sint上层质量块不确定部分Δm1（t）/kg10中间质量块m2/kg105.42上层弹簧线性系数k11/（N·m-1）5.7×106上层弹簧非线性系数k12/（N·m-3）1.6×105下层弹簧系数k2/（N·m-1）1.90×106上层阻尼器系数c1（t）/

（N·s·m-1）0.1+

0.05e-0.1t下层阻尼器系数c2/（N·s·m-1）0.1静态时弹簧变形δ0/m-0.165为了解决这个矛盾，只有在辨识精度与控制的实时性之间做一个折中，进行反复多次实验，找到二者之间一个最佳结合点。在仿真中，混合非随机激励的情况下，项数n=26，而伪随机信号激励的情况下，项数n=32。

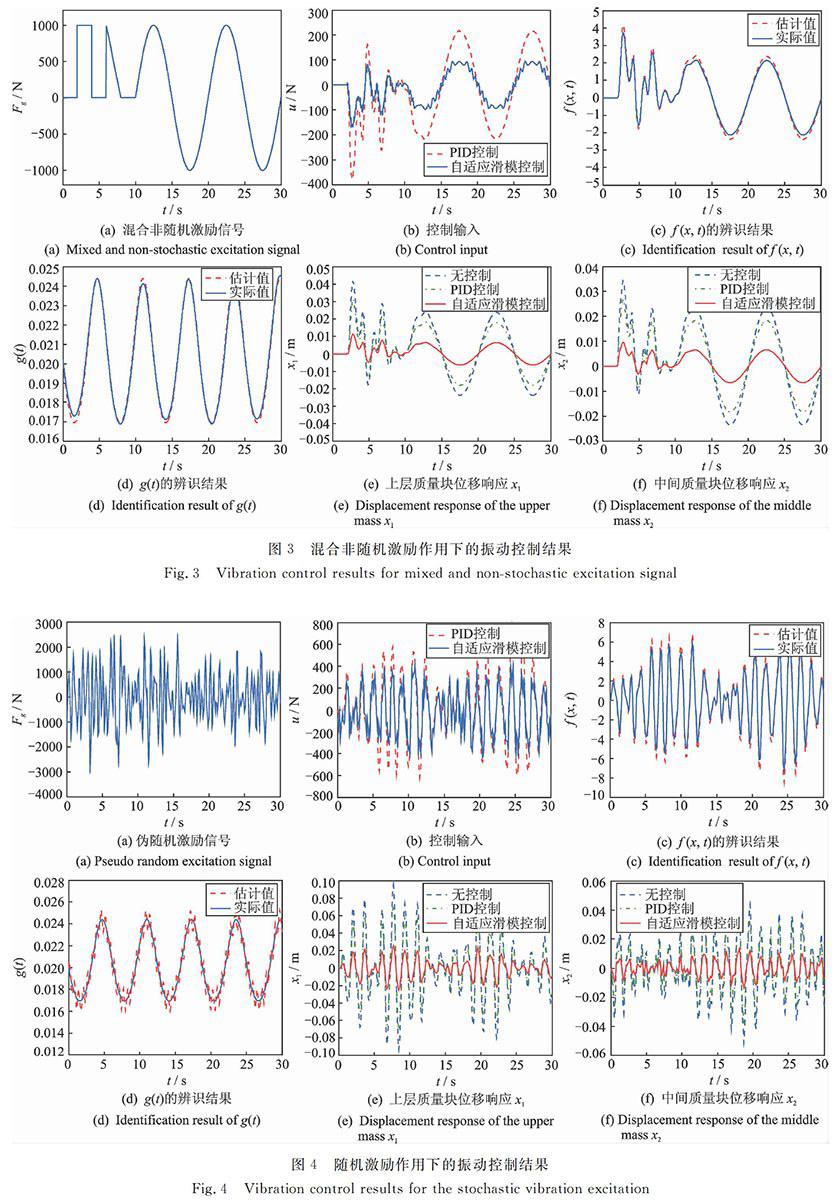
4.1混合非随机激励的振动控制仿真

在工程实际中，常见的激励信号有脉冲激励、阶跃激励、三角波以及简谐激励等，为验证文中提出的方法在各种常规激励作用下的控制效果，采用一组由方波、三角波和简谐波组成的混合信号作为系统的激励信号[1920]Fg（t）=1000，t∈[2，4）

500（8-t），t∈[6，8）

1000sin0.2π（t-10），t∈[10，18）

0，其他隔振系统在混合非随机激励作用下的控制效果如图3所示。

4.2伪随机信号激励的振动控制仿真

随机激励是振动工程领域常见的激励方式，在振动控制实验中能够充分激励隔振系统的各种模态。在保持系统物理参数与控制器参数不变的情况下，得到如图4所示的双层隔振系统在伪随机激励作用下的控制效果。

由图3（c）～（d）和4（c）～（d）可知，基于正交函数的辨识方法能够很好地辨识系统时变参数与未知载荷，对未知函数f（x，t）与g（t）具有较强的估计能力。但是，系统对未知函数的估计精度随着外激励信号的不同而不同，随机激励由于前后时刻之间的信号不相关导致其估计精度比非随机激励信号低。

由图3（e）～（f）和4（e）～（f）可知，傳统PID控制方法对系统的控制效果十分有限，而基于正交函数近似方法的自适应滑模控制方法可以使系统控制后的位移由常规PID控制时的80%～85%降低到40%以内。同时，由图3与4可以看出，系统的控制精度随着外激励信号的不同而有所不同，随机激励由于前后时刻之间的信号不相关导致其控制精度比非随机激励信号要低一些。

图3与4反映了双层隔振系统未知载荷估计和控制效果，该系统分别受到规则简谐信号和随机输入信号的激励作用，采用正交函数近似方法可以很好地估计出系统的不确定部分，辨识精度较高。由于控制系统具有不确定部分在线估计功能，所设计的自适应滑模控制方法的控制效果明显优于常规PID控制方法。图3混合非随机激励作用下的振动控制结果

Fig.3Vibration control results for mixed and nonstochastic excitation signal

图4随机激励作用下的振动控制结果

Fig.4Vibration control results for the stochastic vibration excitation5双层隔振系统实验验证

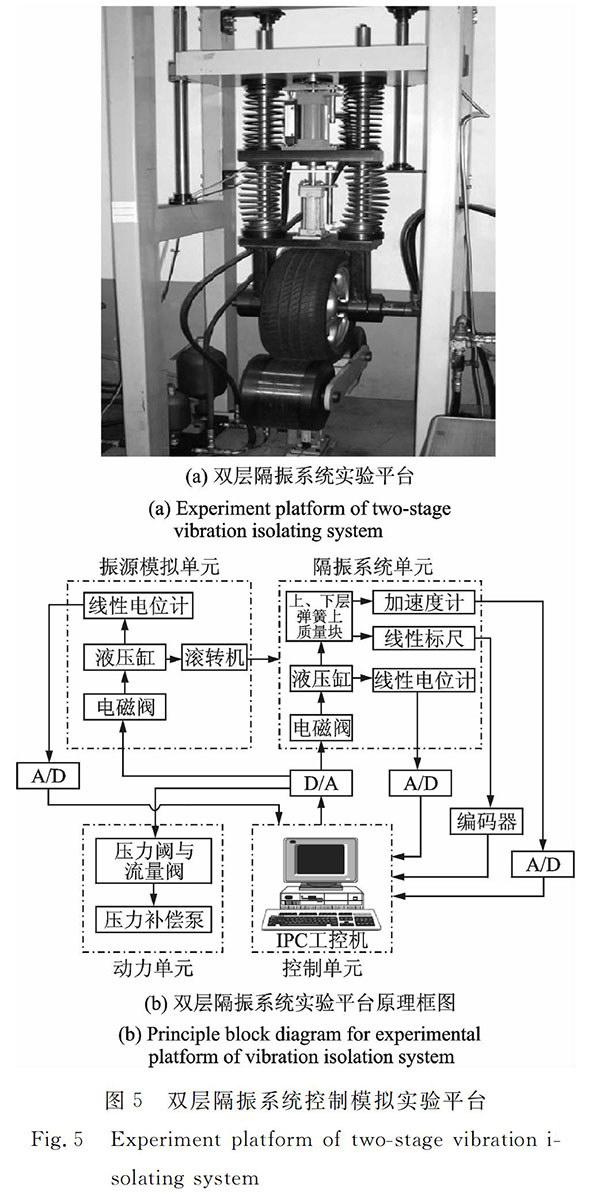
双层隔振主动控制系统的实验平台与结构原理框图如图5所示。实验装置主要有两部分组成：一个是振源模拟单元，主要模拟振源产生的激振信号，也就是迫使隔振系统振动的外激扰力；另一个是隔振系统的检测与控制单元，主要是振动信号检测与控制力产生。由IPC工业控制计算机产生的激振信号经A/D转换器送入由电磁阀、液压机与滚转机组成的激振器，模拟初级振源的振动。在未实施控制前，先由安装于下层质量的加速度传感器测量并记录下层质量的响应，以了解被动隔振的情况。实施主动控制时，由传感器测得的位移与加速度信号

图5双层隔振系统控制模拟实验平台

Fig.5Experiment platform of twostage vibration isolating system经过低通滤波及A/D转换后作为自适应滑模控制器的输入。控制器输出分别驱动两个液压缸作动器对系统进行控制。控制器硬件由工业控制计算机IPC610H以及研华PCM3718高速智能数据采集卡构成，控制软件用C++语言编制。

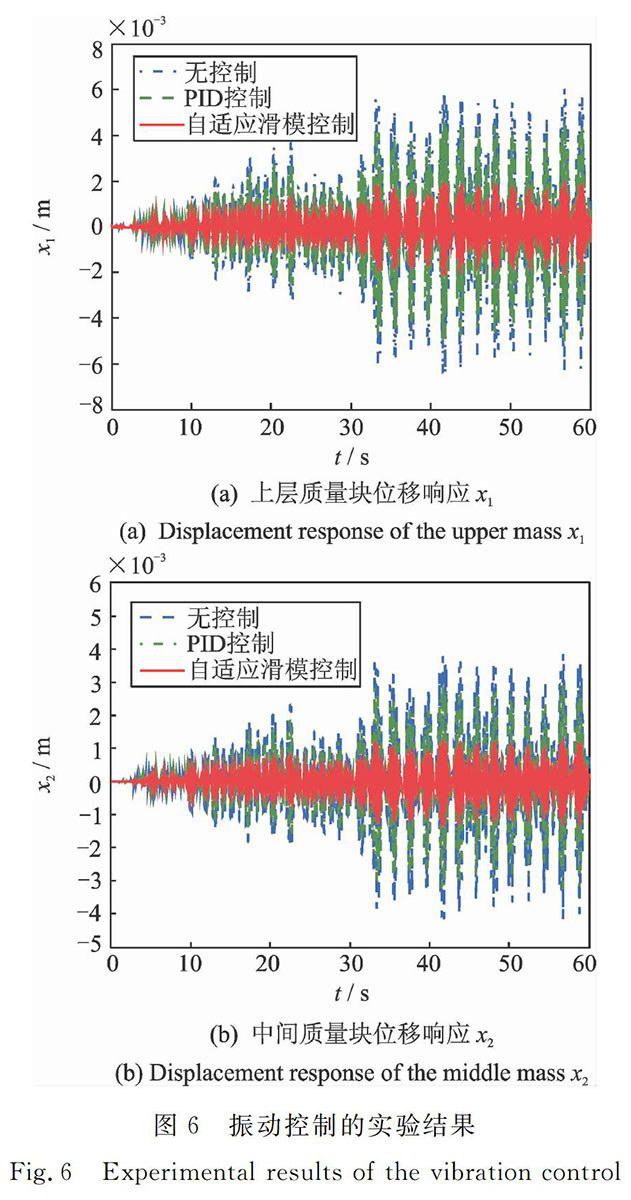
在进行振动控制实验时，由振源模拟单元产生频率为5 Hz的单位正弦信号作为初级振源输入进行主动控制模拟试验。实验平台参数如下：上层质量块m1=105 kg，上层质量块不确定部分Δm1=10 kg，中间质量块m2=55 kg，上层弹簧线性系数k11=5.7×106 N/m，上层弹簧非线性系数k12=1.6×105 N/m3，下层弹簧系数k2=1.90×106 N/m，上下层阻尼器系数c1=c2=170 N·s/m。实验中，ASMC控制器参数选择如下：λ1=2.0，λ2=1.0，λ3=λ4=1.5，饱和函数边界层厚度δ=0.08。PID控制器参数：比例系数kp=2.5，积分系数ki=0.3，微分系数kd=0.08。正交函数的基函数项数n=20。两种控制方法的实验对比结果如图6所示。

图6振动控制的实验结果

Fig.6Experimental results of the vibration control

由图6可知，施加主动控制后，应用自适应滑模控制方法能够使上下层质量块的振动衰减量达75%～80%左右，采用常规PID控制可以使质量块的振动衰减量达30%～35%左右。由此可见，所设计的自适应滑模控制策略对双层隔振系统进行控制时具有较强的抑制单频信号的能力，控制效果明显优于常规PID控制，适用于工程应用。

6结论

针对双层隔振系统载荷与参数不确定的特性，提出了将正交函数近似方法与滑模控制相结合应用于双层隔振系统有源控制的新方法。该方法利用正交函数近似法对系统的不确定部分进行在线估计，通过自适应滑模控制器在线计算控制力。仿真与实验结果都表明这种自适应滑模有源振动控制策略是行之有效的。另外，系统误差是评价一个振动控制系统控制效果的重要指标，其分析方法是振动控制评价的重要研究内容，作者正在做振动系统的误差分析与减振效果评价等方面开展相关研究。

参考文献：

[1]杨铁军，顾仲权，刘志刚，等.双层隔振系统耦合振动主动控制实验研究[J].振动工程学报，2003，16（2）： 149—152.

YANG Tiejun， Gu Zhongquan， Liu Zhigang， et al. Experimental research on active control of coupled vibration for a twostage isolation system [J]. Journal of Vibration Engineering， 2003， 16（2）：149—152.

[2]高宏伟，罗军，贾建援. 双层隔振系统主动控制的建模与仿真[J].机械科学与技术， 2005， 24（11）： 1340—1342.

GAO Hongwei， Luo Jun， Jia Jianyuan. Modeling and simulation of active control of twolayer vibration isolation system [J]. Mechanical Science and Technology， 2005， 24（11）： 1340—1342.

[3]钟民军，胡世峰，史铁林，等.双层混合隔振系统的CMAC和PID复合控制研究[J].中国机械工程，2008，19（13）： 1547—1551.

ZHONG Minjun， Hu Shifeng， Shi Tielin， et al. Study on the Compound Control of CMAC and PID to the Hybrid Two Stage Vibration Isolation System [J]. China Mechanical Engineering， 2008， 19（13）： 1547—1551.

[4]袁紹军， 杨铁军， 肖友洪， 等. 双层隔振系统量化因子模糊自调整主动控制技术研究[J]. 振动工程学报， 2005， 18（2）： 208—211.

YUAN Shaojun， YANG Tiejun， XIAO Youhong， et al. Study on scaling factor fuzzy selftuning active control technology to a twostage isolation system [J]. Journal of Vibration Engineering， 2005， 18（2）： 208—211.

[5]Zhao C S， Zhu S J， He Q W. FuzzyPID control method for twostage vibration isolation system [J]. Journal of Theoretical and Applied Mechanics， 2007， 45（1）： 171—177.

[6]Yagiz N， Hacioglu Y. Backstepping control of a vehicle with active suspensions [J].Control Engineer Practice， 2008， 16 （12）： 1457—1467.

[7]RodriguezFortun J M， Orus J， Alfonso J， et al. Flatness based active vibration control for piezoelectric actuators [J]. IEEE Transactions on Mechatronics， 2013， 18 （1）： 221—229.

[8]杨铁军，刘志刚，张文平，等.基于xRLMS算法的自适应有源隔振技术研究[J].内燃机学报， 2001， 19（1）： 92—95.

YANG Tiejun， LIU Zhigang， ZHANG Wenping， et al. Investigation in active vibration isolation based on xRLMS algorithm [J]. Transactions of CSICE， 2001， 19（1）：92—95.

[9]鲁民月， 顾仲权， 杨铁军. 简化的结构振动自适应前馈控制方法研究[J].振动与冲击， 2005，24（1）： 98—93.

LU Minyue， Gu Zhongquan，Yang Tiejun. Study on simplified adaptive feed forward control for vibration reduction of structures [J]. Journal of Vibration and Shock， 2005， 24（1）：98—93.

[10]Riyanto B. Realtime DSP implementation of active noise control for broadband noise using adaptive LMS filter algorithm[C]. Proceedings of the International Conference on Electrical Engineering and Informatics Institut Teknologi Bandung， Indonesia， June， 17—19， 2007.

[11]Landau I D， Alma M， Airimitoaie T B. Adaptive feedforward compensation algorithms for active vibration control with mechanical coupling[J]. Automatica， 2011， 47（10）： 2185—2196.

[12]曾强洪， 朱石坚， 楼京俊，等. 基于滑模控制投影混沌同步在隔振系统中的应用研究[J]. 振动与冲击， 2010， 29（12）： 114—117.

ZENG Hongqiang， ZHU Shijian， LOU Jingjun， et al. Applica tion of projective synchronization to vibration isolation system based on sliding mode control [J]. Journal of Vibration and Shock， 2010， 29 （12）： 114—117.

[13]刘延斌， 韩秀英， 马佳佳，等. 基于气动肌肉和负刚度机构的主、被动宽频隔振研究[J]. 振动与冲击， 2014， 33（24）： 179—186.

LIU Yanbin， HAN Xiuying， MA Jiajia， et al. Active and passive broadfrequency vibration isolation based on PAM and negative stiffness element [J]. Journal of Vibration and Shock， 2014， 33（24）：179—186.

[14]赵成， 胡增荣， 陈大跃. 半主动悬架的滑模变结构控制[J]. 中国公路学报， 2007， 20（3）： 109—114.

ZHAO Cheng， HU Zengrong， CHEN Dayue. Sliding mode varying structure control for semiactive suspension [J]. China Journal of Highway and Transport， 2007， 20 （3）： 109—114.

[15]Zhang H， Wang E， Ning Z， et al. Semiactive sliding mode control of vehicle suspension with magneto rheological damper [J]. Chinese Journal of Mechanical Engineering， 2015， 28（1）：63—75.

[16]Han W， Reddy B D. Plasticity： Mathematical Theory and Numerical Analysis [M]. Springer， 2012.

[17]Huang S J， Huang H Y. Adaptive sliding controller with selftuning fuzzy compensation for vehicle suspension control [J]. Mechatronics， 2006， 16（6）： 607—622.

[18]Slotine J， Li W. Applied Nonlinear Control [M]. New Jersey： PrenticeHall， 1991.

[19]邵敏強， 陈卫东， 陈前.基于随机游走和输入估计方法的振动主动控制研究[J].振动与冲击，2009，28（7）： 55—60.

SHAO Minqiang，CHEN Weidong，CHEN Qian. An active vibration control method based on random walk and input estimation algorithm[J]. Journal of Vibration and Shock， 2009， 28（7）：55—60.

[20]严济宽. 机械振动隔离技术[M]. 上海：上海科学技术文献出版社， 1986.

YAN Jikuan. Mechanical Vibration Isolation[M]. Shanghai：Science and Technology Documents Press of Shanghai， 1986.

Adaptive sliding mode control for twostage vibration

isolating system with timevarying loads

CUI Mingyue1，2， LIU Hongzhao1，2， QU Chongnian1，2， SUN Dihua3

（1.School of Mechatrionics Engineering， Nanyang Normal University， Nanyang 473061， China；

2.Oil Equipment and Intelligent Control Engineering Laboratory of Henan Province， Nanyang 473061， China；

3.College of Automation， Chongqing University， Chongqing 400044， China）

Abstract： An adaptive sliding controller is proposed in this paper for controlling a twostage vibration isolating system with timevarying loads. The reference coordinate is placed at the static position under the nominal loading so that the system dynamic equation is derived. Due to spring nonlinearities， the system property becomes asymmetric after coordinate transformation. Besides， in practical cases， system parameters are not easy to be obtained precisely for controller design. Therefore， in this paper， system uncertainties are lumped into two unknown timevarying functions. To estimate the unknown timevarying functions online， the orthogonal function approximation technique is employed to represent the unknown function as a finite combination of basis functions. The Lyapunov's direct method is used to derive adaptive laws for updating coefficients in the approximating series and to prove stability of the closedloop system. The simulation and experiment results demonstrate that the control performance of the present method for structure greatly compensates the effects of timevarying load sand parameter uncertainties and improves control effectiveness， in comparison with the conventional PID approach.Key words： active control； twostage vibration isolation system； orthogonal function approximation method； adaptive sliding mode control作者简介： 崔明月（1974—），男，博士，讲师。电话：（0377）63525159；Email：cuiminyue@sina.com