结构等间距布置对圆柱壳结构振动性能的影响

谭路 纪刚 周其斗 张纬康 刘文玺

摘要： 为研究圆柱壳结构等间距结构振动性能的一般规律，以有限元法对多个等间距加肋圆柱壳模型的振动响应进行了计算，对其均方法向速度级传递函数进行了分析，并采用波数谱分析方法将壳体振动在波数域上进行了波形分离与量化，分别对壳体轴向与周向的一般振动特性进行了总结，从波动的视角解释了其机理。研究表明：肋骨的布置形式与结构参数仅在结构波长与肋间距相当的中高频才对壳体振动产生较大影响，并使得振动在频域上表现为交替存在通带与止带的特征。肋骨间距增大使得通带向低频偏移，肋骨厚度增大使得通带处的结构波衰减增大。关键词： 结构振动； 圆柱壳； 等间距； 波数谱

中图分类号： U661.44； O427文献标志码： A文章编号： 10044523（2017）04060307

DOI：10.16385/j.cnki.issn.10044523.2017.04.011

1概述

结构等间距布置的圆柱壳是航天工程与海洋工程领域的常见结构[1]，如等间距加肋圆柱壳、等间距分舱圆柱壳。由于航天飞行器与水下航行器在实际应用中对结构振动性能提出了较高要求，因此开展圆柱壳结构等间距结构振动性能研究对优化结构的振动与声辐射特性具有重要意义。

等间距结构的振动特性研究多集中于20世纪八、九十年代，主要由国外少数学者D J Mead[13]，G Maidanik[45]，B R Mace[67]等开展，这些研究以解析法为主要计算方法，重点对一维等间距梁结构[811]与二维等间距加肋板[1216]的振动特性进行了研究。这些研究得出的主要结论有两点：（1）等间距结构在振动时，结构波的传播需满足布洛赫理论，即任意相隔周期间距的两点A和B的状态向量（包含六个自由度的位移与相应受力的信息）幅值A，B之比恒定，相位差恒定，幅值與相位的变化可通过传播常数μ来表示[1718]B=eμ×A=eμr+jμi×A（1）传播常数通常可用复数形式表达，其中实部μr为衰减常数，描述结构波在传播中的衰减情况，虚部为相位差常数μi，描述了结构波在传播中的相位变化情况。（2）简单等间距结构（如等间距简支支撑梁、单向等间距加肋板）的振动在频域上有交替存在通带与止带的特征，其中通带代表结构波能自由传播时的频带，即衰减常数为0，止带代表随传播距离的增大结构波幅值成指数衰减的频带，即衰减常数不为0[1920]。上述研究多针对简单结构进行，针对圆柱壳结构等间距加肋的相关研究较少。而目前关于加肋圆柱壳结构振动性能的研究多将其作为一个整体进行研究，尚未有研究深入分析肋骨布置形式对壳体振动的影响，且并未从物理意义上解释清楚结构等间距布置影响圆柱壳结构振动性能的机理。

本文以等间距加肋圆柱壳作为一般等间距结构布置圆柱壳的具体化对象，采用有限元方法计算获得壳体振动响应，以此为输入获得壳体均方法向速度级传递函数。为识别结构振动的各简谐波分量，从波动的视角解释结构变化引起振动响应变化的机理，应用波数谱分析方法得出壳体的法向速度振动功率波数谱，通过对均方法向速度级传递函数与波数谱的分析，总结获得结构等间距布置对圆柱壳结构振动性能的影响规律及其机理。其中有限元计算方法与传递函数理论不再赘述，重点介绍波数谱分析方法。

2圆柱壳的波数谱分析理论[*2]2.1振动的波形分离应用有限元方法计算获得圆柱壳的振动响应，假设在圆柱壳两端存在无限长的柱屏[21]，则壳体的振动响应在全域可表示为w（x，θ）=wR+jwI，x∈[0，l]

0，x[0，l] （2）式中x和θ分别为圆柱壳的轴向与周向坐标；wR和wI分别为壳体法向位移实部与虚部；l为圆柱壳长；j=-1为虚部单位。分别对wR和wI在周向进行傅里叶级数展开，并在轴向进行傅里叶变换，得：wR=1〖〗2π∑∞n=0{∫+∞-∞[ARn（kx）cosnθejkxx+

BRn（kx）sinnθejkxx]dkx}

wI=12π∑∞n=0{∫+∞-∞[AIn（kx）cosnθejkxx+

BIn（kx）sinnθejkxx]dkx}（3）式中kx和n分别为轴向波数与振动沿周向的谐波数。藉此，圆柱壳上的振动场被分解为具有不同波数的简单行进波的叠加，ARn，BRn，AIn和BIn即代表这些简单波幅值的大小。

第4期谭路，等： 结构等间距布置对圆柱壳结构振动性能的影响振 动 工 程 学 报第30卷2.2法向速度振动功率波数谱

将式（2）中壳体法向位移变换为法向速度，并将速度的平方在圆柱壳表面上积分，得到整个圆柱壳以法向速度表达的振动功率，简称为壳体的法向速度振动功率

Etv=ρ0c0ω22∫l0∫2π0[wR2+wI2]rdθdxr=a（4）

式中ρ0和c0分别为流体的密度与声速；a为圆柱壳半径。式中乘上声阻抗ρ0c0，是为了将量纲变换为功率单位而引入，它不会改变振动功率的频率特性。本文中的流体均指空气。将式（3）代入式（4），并通过巴赛瓦（Parseval）等式进行简化，可得[22]：Etv=aρ0c0ω2∫+∞0 ARn（kx）2+

AIn（kx）2dkx，n=0

aρ0c0ω2∫+∞0 ARn（kx）2+AIn（kx）2dkx+

∑∞n=1aω2ρ0c02∫+∞0 ARn（kx）2+

AIn（kx）2+BRn（kx）2+

BIn（kx）2]dkxn≠0（5）因为总的法向速度振动功率也可表示为各波数为（n，kx）的波分量的法向速度振动功率的叠加，即：Etv=∑∞n=0∫+∞0Ev（n，kx）dkx，kx≥0（6）因此，根据式（5）和（6）可得法向速度振动功率单边谱Ev（n，kx）：Ev（n，kx）=aρ0c0ω2ARn（kx）2+

AIn（kx）2，n=0

aρ0c02ω2ARn（kx）2+

AIn（kx）2+BRn（kx）2+

BIn（kx）2，n≠0（7）进一步，与周向谐波数为n相对应的结构振动（下文简称为n阶振动）的法向速度振动功率为：

Env=∫+∞0Ev（n，kx）dkx=

aρ0c0ω2∫+∞0 ARn（kx）2+

AIn（kx）2dkx，n=0

aρ0c0ω22∫+∞0 ARn（kx）2+

AIn（kx）2+BRn（kx）2+

BIn（kx）2dkx，n≠0（8）

3等间距加肋圆柱壳轴向波数谱分析

以周向n=0阶的振动模式为例，对圆柱壳轴向的振动特性进行分析。选取不同间距的等间距加肋圆柱壳作为分析模型，圆柱壳壳厚6 mm，舱壁厚30 mm，肋骨厚20 mm，高300 mm，如图1所示。

图1等间距加肋圆柱壳结构示意图

Fig.1Periodic ribbed cylindrical shell三个等间距加肋圆柱壳的肋骨间距分别为500，600，700 mm。模型全部采用钢材料，其杨氏模量为2.05×105 N/mm2， 密度为7.80×10-6kg/mm3，泊松比为0.3。

为方便分析，在圆柱壳左端施加环形均匀的径向激励，激励幅值为1 N（如图1所示）。此时，圆柱壳振动以周向n=0阶的振动模式为主。

图2等间距加肋圆柱壳均方法向速度级传递函数频率曲线

Fig.2Mean square velocity level transmission function of periodic ribbed cylindrical shell图2为三个模型的壳体均方法向速度级传递函数（激振力幅值为1 N时的壳体均方法向速度级）频率曲线。由于激励源处结构振动较强，为防止结构整体振动特征被湮没，仅选取距激励端两个肋间距之后的所有壳体节点振动响应计算壳体均方法向速度级传递函数。易见：三个模型的均方法向速度级传递函数在低频时相似，在中高频有较大区别。其物理机理为：低频时结构波长较长，肋骨布置形式对壳体总振动影响较小，随着频率增高，结构波长变短，肋骨布置形式对壳体振动的影响才体现出来；同理可以推论，由于舱壁间距较大，因此舱壁布置形式将对更低频段壳体振动产生影响。

为解释产生上述现象的原理，以肋骨间距为600 mm的圆柱壳模型为例，对其谱峰频率为391，469，637，862 Hz处的壳体振动在轴向上进行波数谱分析。

图3等间距加肋圆柱壳在典型频率处的周向n=0阶法向速度振动功率波数谱

Fig.3The normal velocity vibration power wavenumber spectrum of periodic ribbed cylindrical shell in typical frequencies corresponding to n=0圖3为典型频率处壳体周向为n=0阶的法向速度振动功率波数谱，其中壳体轴向无因次波数为12lkx/π，易见：（1）各典型频率处，壳体轴向振动波数谱的谱峰波数相同，根据结构振形可知，谱峰处对应的壳体振动结构波长均为1/m（m为正整数）倍肋间距；（2）在469，862 Hz，等间距圆柱壳主要轴向振动无因次波数对应的结构波长分别为1/1倍与1/2倍肋间距，与结构振形相符，如图4所示；（3）在391，637 Hz，虽然壳体轴向振动的主要结构波长分别为1/0.5，1/1.5倍肋骨间距（见图4），但由于肋骨两侧壳体振动的相位并非恒定相反，因此391 Hz时波数谱上显示主导肋间振动的波长为1倍肋骨间距，而637 Hz时主导肋间振动的波长分布在1/1～1/2倍肋间距区间；（4）肋骨的等间距布置使得壳体在轴向上以波包形式振动。

图4典型频率下的等间距加肋圆柱壳结构振形

Fig.4Vibration shapes of periodic ribbed cylindrical shell in typical frequencies通过壳体轴向波数谱分析可知，在各典型频率处，壳体的肋间轴向振动依次以1，2，3，4倍半波振动为主。根据等间距结构振动理论可知，通过振形判定结构振动处于通带需满足两个条件：（1）结构波能自由传播，结构波幅值随传播距离增大并无明显衰减；（2）等间距结构的子结构（等间距加肋圆柱壳的子结构为相邻肋骨间壳体及两端各自1/2厚度的肋骨）近似以整数倍半波振动为主。因此，可以判定上述典型频率所在的谱峰频段依次为第一至第四通带，通带之间为止带。

根据上述分析结论，对图2分析可知：（1）三个模型在中高频均显现出波峰波谷交替现象，这是由等间距加肋圆柱壳的振动在频域上交替存在通带与止带的特性引起的；（2）肋间距不同的壳体，对同一通带其主要轴向结构波波长为相同倍数的肋间距。因此对同一通带，肋间距越大，则对应的结构波波长越长，使得通带向低频偏移。图中已标记出各模型轴向振动主要结构波波长为1/1.5倍肋间距的谱峰。虽然通带的偏移并未使得普峰值减小，但却改变了壳体的结构振动频率特性。（3）由于低频段波峰波谷产生的原因并非由通带与止带引起，因此各肋间距不同壳体的低频波峰波谷并无偏移。

4等间距加肋圆柱壳周向波数谱分析

选取如图1所示等间距加肋圆柱壳结构，去除两端端盖后作为分析模型，肋骨间距为600 mm。在模型左端施加垂直的简谐点激励，激励幅值为1 N，若将此种激励在周向上进行空间域的分解，可当作多种周向阶数模式的环形径向激励的叠加，且各模式激励的幅值相当，有利于后续对壳体各周向阶振动的特性进行分析。同理，若圆柱壳在端部添加端盖，在垂向激励下，壳体响应则以周向n=1阶的振动模式为主，不利于各周向阶振动模式的比较分析，因此模型不加端盖。

图5等间距加肋圆柱壳周向为n=0，3，6，9阶的法向速度振动功率

Fig.5The nomal velocity vibration power of periodic ribbed shell corresponding to n=0，3，6，9

图5为等间距加肋圆柱壳周向为n=0，3，6，9阶法向速度振动功率频率曲线，易见：（1）在较宽频带内，壳体各周向阶振动均对总振动有较大贡献，并非以单一周向阶振动为主，表现为多模式振动的特征；（2）对任意周向阶振动，等间距圆柱壳在频域上均表现有通带与止带交替存在的特征；（3）图中标记A，B，C，D分别为各周向阶法向速度振動功率频率曲线的四组谱峰，其相应壳体轴向振动主要结构波长分别为1/0.5，1/1，1/1.5，1/2倍肋骨间距，由图可知，周向振动阶数升高，其相应的低阶通带向低频偏移，高阶通带的频率范围则变化不大；（4）结构总振动是各周向阶振动的叠加，对不同的激励方式，结构各周向阶振动对总振动的贡献不同，由于各周向阶振动对应的低阶通带频率范围不一致，因此结构总振动显现出的低阶通带与止带特征不同。

5肋骨结构参数对等间距加肋圆柱壳结构振动特性影响研究5.1肋骨尺寸对壳体振动特性的影响为方便从机理上理解肋骨参数对壳体振动的影响，采用矩形截面的肋骨，其主要几何参数为厚度与高度。由于肋骨径向强度与肋骨截面的面积近似成线性关系，因此为保证肋骨径向强度，需在保证肋骨截面面积不变的条件下对肋骨几何参数进行研究。

以三个肋骨截面面积相同但肋骨尺寸不同的加肋圆柱壳为例，对其结构声学性能进行对比分析。三个模型的主尺度均与图1中的等间距加肋圆柱壳相同，肋骨间距为600 mm，仅肋骨尺寸不同，肋骨高度分别为150，300，450 mm，肋骨厚度分别为12，6，4 mm。令肋骨的高度与厚度之比为无因次肋骨尺寸参数Rdim1，即各模型的无因次肋骨尺寸参数为12.5，50，112.5。

以图1中激励为例，对不同肋骨尺寸的等间距加肋圆柱壳结构振动性能进行对比分析。计算时模型采用自由边界条件。选取距激励端两个肋间距之后的所有壳体上的节点振动响应计算圆柱壳的均方法向速度级传递函数。

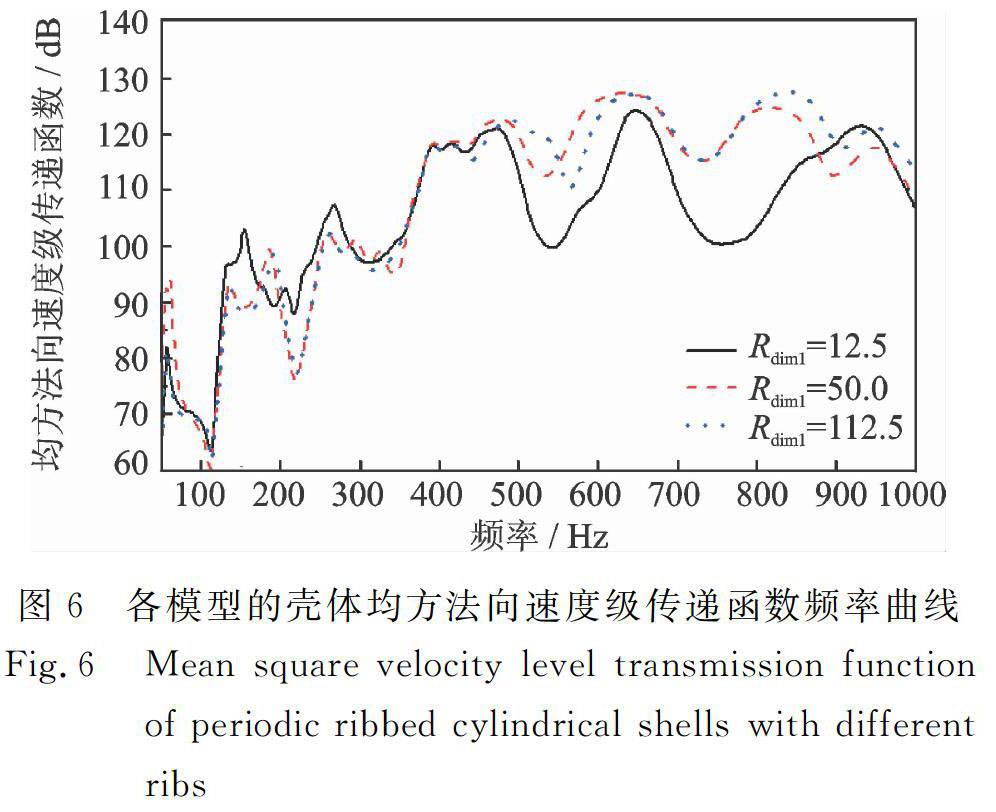
图6各模型的壳体均方法向速度级传递函数频率曲线

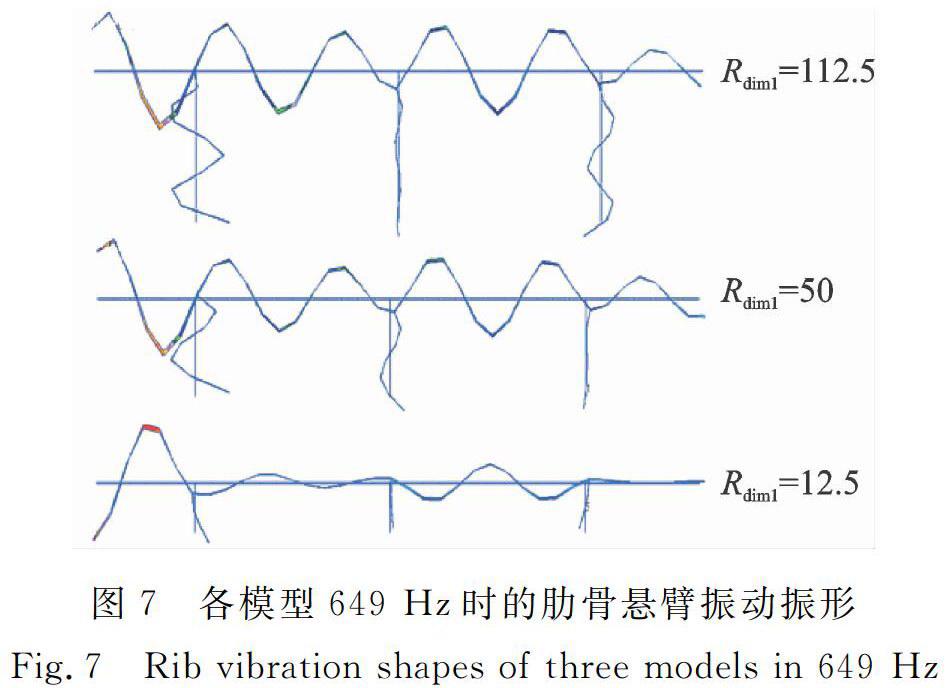
Fig.6Mean square velocity level transmission function of periodic ribbed cylindrical shells with different ribs图6为各肋骨截面面积相同但尺寸不同的圆柱壳模型的均方法向速度级传递函数频率曲线。易见：（1）肋骨尺寸的变化使得各曲线在中高频发生了较大的变化，即其对等间距加肋圆柱壳振动的影响主要体现在通带与止带频段内。（2）肋骨尺寸变化主要影响了壳体通带与止带的振动大小，对其频率特性影响不大。（3）由于各种类肋骨截面面积相同，径向强度近似，因此产生上述影响主要是由于不同肋骨对加肋处壳体的转动导纳影响不同。壳体振动引起的肋骨悬臂振动将反作用于壳体，使得壳体在加肋处的转动导纳降低。对理想无阻尼情况，在通带内结构波仍能无衰减的传播，加肋处壳体转动导纳降低并不能加大结构波的衰减，但却能使整体结构波的幅值降低，因此降低加肋处壳体转动导纳有利于抑制壳体振动。（4）Rdim1=50与Rdim1=112.5的模型的曲线变化不大，其原因为两肋骨在该频率下均做高阶悬臂振动，其对加肋处壳体的转动导纳影响相近。但对肋骨高度较小，厚度较大Rdim1=12.5的模型，其肋骨做一阶悬臂振动，反而使得壳体的转动导纳降低幅度较大，对振动的抑制较为明显，如图7所示。（5）截面矮厚型的肋骨相较于截面高薄形的肋骨对抑制壳体振动较优，但并非肋骨越矮越厚则越好，例如对同样做一阶悬臂振动的肋骨，截面高薄形肋骨对壳体转动惯量的增量较大，使得加肋处壳体的转动导纳更小，更有利于抑制壳体的振动。

图7各模型649 Hz时的肋骨悬臂振动振形

Fig.7Rib vibration shapes of three models in 649 Hz5.2肋骨截面形状对壳体振动特性的影响

工程实际中常用肋骨的截面除矩形外还有T形，该种肋骨截面形状可在保证肋骨径向强度的基础上有效节省圆柱壳内部空间。以三个肋骨截面面积相同但肋骨截面形状不同的加肋圆柱壳为例，对比分析具有矩形截面和T形截面肋骨的圆柱壳的结构振动性能。

三个模型的主尺度均与图1中的等间距加肋圆柱壳相同，肋骨间距为600 mm，仅肋骨截面不同，其中矩形截面肋骨厚12 mm，高150 mm；T形截面肋骨有两种，一种T形截面肋骨腹板厚11 mm，高100 mm，翼板厚11 mm，宽64 mm；另一种T形截面肋骨腹板厚7.3 mm，高150 mm，翼板厚7.3 mm，宽96 mm。令T形肋骨腹板的高度与厚度之比为无因次T形肋骨尺寸参数Rdim2，即2种T形肋骨的无因次T形肋骨尺寸参数为9.1，20.5。

以图1中激励为例，对不同肋骨尺寸的等间距加肋圆柱壳结构振动性能进行对比分析。计算时模型采用自由边界条件。选取距激励端两个肋间距之后的所有壳体上的节点振动响应计算圆柱壳的均方法向速度级传递函数。

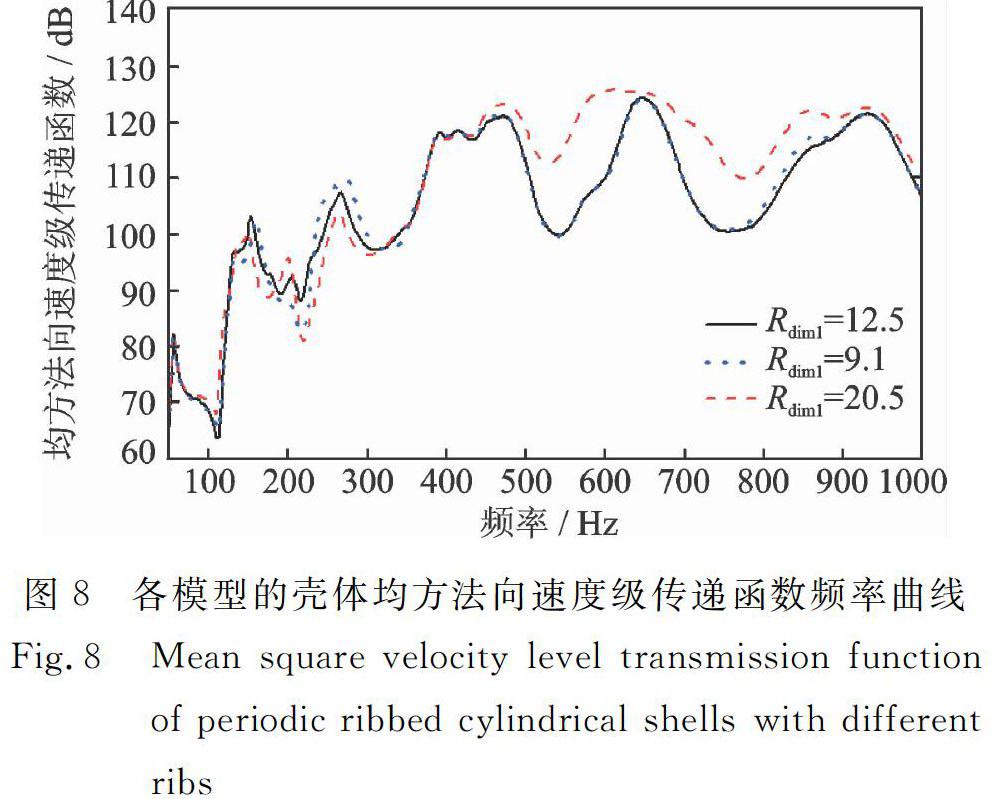
图8为具有矩形与T形截面肋骨的圆柱壳的均方法向速度级传递函数频率曲线。易见：（1）肋骨变化对等间距加肋圆柱壳振动的影响主要体现在通带与止带频段内，且具有矩形与T形截面肋骨的圆柱壳壳体振动具有相似的频率特征，但振动大小不同。（2）矩形截面Rdim1=12.5的肋骨相比于T形截面Rdim2=20.5的肋骨更有利于抑制壳体的振动，其原因为当两肋骨的高度相同时，由于T形截面肋骨腹板较薄，易做高阶悬臂振动，对加肋处壳体的转动导纳影响反而较小。（3）矩形截面Rdim1=12.5的肋骨对壳体振动的影响与T形截面Rdim2=9.1的肋骨近似，说明当两肋骨厚度均较大时，其在较宽频段内均做一阶悬臂振动，此时肋骨对加肋处壳体转动导纳的影响相近，但T形截面肋骨更有利于节省圆柱壳内部空间。（4）同为T形截面的Rdim2=9.1的肋骨相比于Rdim2=20.5的肋骨更有利于抑制壳体的振动，其原因与矩形截面肋骨对壳体转动导纳的影响规律相似，T形截面肋骨同样是矮厚型更有利于抑制壳体结构振动。

圖8各模型的壳体均方法向速度级传递函数频率曲线

Fig.8Mean square velocity level transmission function of periodic ribbed cylindrical shells with different ribs6结论

本文以等间距加肋圆柱壳作为一般等间距结构布置圆柱壳的具体化对象，对其轴向与周向振动的一般性规律进行了研究，并讨论了肋骨间距与肋骨尺寸对壳体振动特性的影响，得出主要结论如下：

（1）肋骨布置形式及厚度参数对壳体振动的影响主要体现在结构波波长小于肋间距的中高频，低频时影响不大。

（2）在中高频段，等间距结构布置使得壳体振动具有交替存在通带与止带的特征。在通带，结构波能自由传播，结构整体振动较强，壳体在轴向上通常以波包形式振动，且肋骨两侧的壳体振动相位并不恒定。

（3）壳体各周向阶振动在频域上同样交替存在通带与止带，但各自对应的通带止带频率范围不同。总振动的通带频率范围为各周向阶振动通带频域范围的叠加，对不同的激励方式，由于结构各周向阶振动对总振动的贡献不同，使得结构总振动显现出的通带与止带特征不同。因此，通过调整激励方式可调节通带的频率范围，尤其是低次序通带的频率范围。

（4）肋骨间距增大，则通带向低频偏移，可通过此规律人为调节壳体的结构振动频率特性。

（5）肋骨尺寸与形状的变化对壳体振动的频率特征影响较小，但对壳体在通止带处的振动大小有较大影响。在保证肋骨径向强度不变的条件下，矮厚型的矩形或T形截面肋骨更有利于抑制壳体振动。

参考文献：

[1]陈美霞，张聪，邓乃旗，等.波传播法求解低频激励下水中加端板圆柱壳的振动[J].振动工程学报，2014，27（6）：842—851.

Chen Meixia，Zhang Cong，Deng Naiqi，et al.Analysis of the low frequency vibration of a submerged cylindrical shell with endplates based on wave propagation approach[J].Journal of Vibration Engineering，2014，27（6）：842—851.

[2]Mead D J.A general theory of harmonic wave propagation in linear periodic systerms with multiple coupling[J].Journal of Sound and Vibration，1973，27（2）：235—260.

[3]Mead D J.Plates with regular stiffening in acoustic media： vibration and radiation[J].The Journal of the Acoustical Society of America，1990，88（1）：391—401.

[4]Maidanik G，Dickey J.Velocity distribution on unloaded finitely and regularly ribbed membranes[J].Journal of Sound and Vibration，1991，149（1）：43—70.

[5]Maidanik G，Becker K J.Potential for the presence of additional stop bands in the modal response of regularly ribbed cylinders[J].Journal of the Acoustical Society of America，1998，104（2）：700—707.

[6]Mace B R.Periodically stiffened fluidloaded plates， I： response to convected harmonic pressure and free wave propagation[J].Journal of Sound and Vibration，1980，73（4）：473—486.

[7]Mace B R.Periodically stiffened fluidloaded plates， II： response to line and point forces[J].Journal of Sound and Vibration，1980，73（4）：487—504.

[8]Mead D J.Wave propagation and natural modes in periodic systems：Ⅰ. monocoupled systems[J].Journal of Sound and Vibration，1975，40（1）：1—18.

[9]Mead D J.Wave propagation and natural modes in periodic systems：Ⅱ. multicoupled systems， with and without damping[J].Journal of Sound and Vibration，1975，40（1）：19—39.

[10]Sen Gupta G.Natural flexural waves and the normal modes of periodicallysupported beams and plates[J].Journal of Sound and Vibration，1970，13（1）：89—101.

[11]Roy A K，Plunkett R.Wave attenuation in periodic structures[J].Journal of Sound and Vibration，1986，104（3）：395—410.

[12]Mead D J，Zhu D C，Bardell N S.Free vibration of an orthogonally stiffened flat plate[J].Journal of Sound and Vibration，1988，127（1）：19—48.

[13]Mead D J，Parthan S.Free wave propagation in twodimensional periodic plates[J].Journal of Sound and Vibration，1979，64（3）：325—348.

[14]Maidanik G，Dickey J.Response of regularly ribbed fluid loaded panels[J].Journal of Sound and Vibration，1992，155（3）：481—495.

[15]Ichchou M N，Berthaut J，Collet M.Multimode wave propagation in ribbed plates： part I， wavenumberapsce characteristics[J].International Journal of Solids and Structures，2008，45：1179—1195.

[16]Ichchou M N，Berthaut J，Collet M.Multimode wave propagation in ribbed plates： part Ⅱ， predictions and comparisons[J].International Journal of Solids and Structures，2008，45：1196—1216.

[17]Ohlrich M.Forced vibration and wave propagation in monocoupled periodic structures[J].Journal of Sound and Vibration，1986，107（3）：411—434.

[18]Mead D J.Wave propagation in continuous periodic structures： research contributions from Southampton， 1964—1995[J].Journal of Sound and Vibration，1996，190（3）：495—524.

[19]Mead D J.A new method of analyzing wave propagation in periodic structures； applications to periodic Timoshenko beams and stiffened plates[J].Journal of Sound and Vibration，1986，104（1）：9—27.

[20]Mead D J，Yaman Y.The response of infinite periodic beams to point harmonic forces： a flexural wave analysis[J].Journal of Sound and Vibration，1991，144（3）：507—530.

[21]WANG C，LAI J C S.The sound radiation efficiency of finite length acoustically thick circular cylindrical shells under mechanical excitation I： Theoretical analysis [J].Journal of Sound and Vibration，2000，232（2）：431—447.

[22]谭路，纪刚，张纬康，等.采用波数域方法分析细长柱壳的振动与声辐射特性[J].海军工程大学学报，2013，25（3）：66—71.

TAN Lu，JI Gang，ZHANG Weikang，et al.Slender cylindrical vibration and radiation by use of wavenumber domain approach[J].Journal of Naval University of Engineering，2013，25（3）：66—71.

Influence of periodic arrangement of structures on structural

vibration characteristics of cylindrical shell

TAN Lu， JI Gang， ZHOU Qidou， ZHANG Weikang， LIU Wenxi

（Dept. of Naval Architecture and Ocean Engineering， Naval Univ. of Engineering， Wuhan 430033，China）

Abstract： Based on the shell vibration response by the finite element method， the mean square velocity level transfer functions of the different cylindrical shells with periodic ribs are obtained. And by using the wavenumber spectrum analysis method， the vibration of the shell is separated and quantified in the wavenumber domain. Then the general vibration characteristics of the shell in the axial and circumferential direction are summarized， and the mechanism of that is explained from the perspective of the wave. Comparing and analyzing the mean square velocity level transfer functions and wavenumber spectrums of different shells， it can be found that the vibration of shell has alternately pass band and stop band only when the structural wavelength is similar to the rib spacing. While the rib spacing increases， the pass band offset to the low frequency. And while the thickness of the rib increases， the propagation attenuation of the structure wave in the pass band is enhanced.Key words： structural vibration； cylindrical shell；periodic；wavenumber spectrum作者簡介： 谭路（1989—），男，博士研究生。电话：15527355418；Email：512425568@qq.com