MT Occam反演的CPU/GPU异构混合并行算法研究

刘 羽,熊壬浩,肖 熠

(桂林理工大学信息科学与工程学院,广西桂林541004)

大量实际计算经验表明,电磁法正反演计算量大,非常耗时,计算速度难以满足当前地质勘查的要求。文献[1]利用单台主流PC机对101×50网格、20观测频率、21测点的二维航空电磁法数据进行正演模拟,耗时4.0～4.5h。文献[2]采用曙光TC5000A单节点对34×34×33网格、16观测频率、25测点的三维MT数据进行反演,运行时间长达47.6h。影响计算速度的主要因素有:①显式的雅可比矩阵计算耗时太多;②当采用有限单元法求解正演响应时,密集的剖分网格会形成巨大的系数矩阵导致计算量陡增;③有些反演方法采用自适应算法求取正则因子,导致迭代次数和总体计算量增加。围绕电磁法计算速度的提升方法,国内外地球物理工作者做了很多算法上的改进[3-5],特别是在并行计算方面,进行了很多探索。2006年,谭捍东等[6]基于频率划分,采用MPI平台实现了大地电磁三维正演的并行计算;同年,刘羽等[7-8]基于频率和拉格朗日乘子划分,在并行计算机(PVM)平台上,实现了二维MT Occam并行反演;陈露军[9]实现了基于MPI的井地三维电磁数值模拟;2009年,SIRIPUNVARAPORN等[10]利用频率划分方式实现了包含垂直磁场转换函数的三维数据空间并行反演;2010—2012年,胡祥云等将并行计算应用于二维大地电磁正演,然后扩展到三维数据空间反演,取得了较好的并行效果[2,11]。

前述并行计算成果均采用了消息传递模型和基于频率划分的大粒度并行方法,当观测频率数较少时,此种方式不具备可扩展并行性,计算性能难以通过增加节点数得到相应提高。例如,文献[6]在4节点集群上获得2.42的加速比(2D prism模型);文献[2]和文献[8]在8节点集群上分别获得5.69和5.65的加速比;文献[10]在8节点和16节点集群上分别获得4.5和7.3的加速比(采用PCG求解器)。可见,要想获得更高计算性能,仅靠扩大集群规模很难奏效。

本文将传统的CPU集群扩展为CPU/GPU异构集群,以MT Occam反演为例,基于不同粒度并行分量的挖掘,实现计算任务的不同层次映射,从而在大粒度并行的基础上进一步提升计算性能。首先给出MT Occam反演的理论方法,然后分析反演方法的并行特征和现有并行方法存在的性能瓶颈,并针对性地提出混合并行方案,利用2种规模的5个理论模型进行了反演测试,给出了方案的实际效果,最后讨论了方案的适用性并给出结论。

1 反演方法

MT Occam反演目标函数可表示为[12-13]:

(1)

式中:μ为拉格朗日乘子;d为观测数据向量;m为模型参数向量;F(m)为模型正演响应;W为归一化矩阵;‖∂m‖2为模型粗糙度,对二维构造,同时考虑了模型的横向和垂向光滑问题,∂=[∂y,∂z]T,其中∂y和∂z分别表示横向和纵向相邻的模型参量的粗糙度矩阵;X2为d与F(m)的拟合差,表示为:

(2)

在迭代寻优中,需要在每一步使用局部线性化[2]。设当前模型为mk,则mk+1的响应为:

(3)

式中:Δm=mk+1-mk为模型的修改量;Jk=(∂F/∂m)k为模型mk处的雅可比矩阵。将(3)式代入(1)式对m求导置零,可得到以μ为变量的模型迭代表达式:

(4)

式中:dk=d-F(mk)+Jkmk。μ值通常使用扫描法或者一维搜索法求得,其取值应使得残差平方和‖Wd-WF[mk+1(μ)]‖2最小。

MT Occam反演是迭代算法,通过不断修改给定的初始模型,使其逐步趋近真实模型。每次迭代通过综合判断拟合差和粗糙度来找出最优解,满足一定条件时,输出模型并结束计算。

2 并行性分析

如前所述,反演迭代计算之间严格顺序依赖关系,无法直接并行实现,因此并行计算只能在一个迭代步内进行。一个迭代步包含模型正演响应F(m)、雅可比矩阵Jk、叉积矩阵、楚列斯基(Cholesky)分解、拉格朗日乘子μ等主要计算项,不同计算项通常具有不同的并行特征,因而需要采用不同的并行策略。

2.1 粗粒度及细粒度并行性

MT Occam反演的一个迭代步内,含有粗粒度和细粒度并行性。非常耗时的雅可比矩阵计算和运行次数极多的模型正演响应计算都是针对频率分别进行的,各频率计算之间无数据耦合,容易基于频率划分实现大粒度并行。当采用扫描方式求取拉格朗日乘子时,μ值点预先按固定间隔选取,其计算相互独立,也可以实现大粒度分解。μ值一维搜索方式下,采用黄金分割法寻找凹区间,新μ值点的确定依赖前点,属于迭代方式,无法直接并行,但可以在正演响应计算部分以分频方式实现并行计算。

细粒度并行性分布于反演过程中不同的计算项。例如,一个频率的模型正演响应计算,需要采用高斯消元法求解形如ax=b的大型线性方程组,其中a为有限单元刚度阵,b为常数项,x为待求向量,消元过程中的行操作可以分解,形成极细粒度计算任务,这些计算可以通过解耦实现并行处理。雅可比矩阵计算也具有同样的特征。此外,每次迭代中,需要完成多个矩阵叉乘运算和多次Chelosky分解,这些部分也都具有极细粒度的并行性。

2.2 传统并行方式的性能瓶颈及解决方案

基于频率和μ值扫描点的分解具有天然的并行性,粒度也可以通过任务组合加以调整,适合消息传递模式下的大粒度并行,是电磁法正反演传统并行计算的主要分解方式,文献[2]、文献[6]和文献[10]都采用了频率划分策略,文献[8]则结合采用了频率划分和μ值扫描点划分。但一般来说,电磁法勘探中的观测频率数有限,通常不会超过40个,反演中μ乘子扫描点数一般也不会超过30个,因此,基于频率和μ值扫描点的大粒度分解方式并行度是受限的[14]。以f表示程序中的串行部分,T1为串行执行时间,假定并行工作由N份大小固定的工作tu组成,每份工作可以与其它工作并行执行,但不再继续细分(一个包含N个观测频率的模型正演及偏导数计算就具有此种特征),则在一个含有p个处理机的并行机上执行程序的时间可以表示为:

(5)

公式(5)中N实际为并行度,当P超过这一并行度时,并行运行时间便不再减少。这暴露出MT Occam反演传统并行方式的性能瓶颈:

1) 当并行度较低时,增加处理机数没有意义。

2) 由于并行度并非远大于处理机数,很难保证所有处理机能几乎平均地分配计算任务,这容易导致短板效应,降低效率。

由此可见,在消息传递模式下,MT Occam反演的并行计算性能由于并行度受限而难以提高。

要继续减小并行计算时间Tp,必须细分tu,即充分利用算法中的细粒度并行性。但不同并行特征的计算只有适应计算机集群的体系结构才能获得最佳的计算效率[15]。在消息传递模式下,tu的细分没有意义,因为计算每个细粒度任务需要进行繁杂的通信,每一次的通信都包含启动时间和传输时间,因此计算/通信比会很小,程序的运行效率非常低下,极端情况下甚至会带来灾难性后果。因此,细粒度并行不适合消息传递模式,需要运行在共享内存架构上,这需要对传统结构进行扩展。

由于对细粒度并行的良好支持,GPU的通用计算技术(GPGPU)发展极为迅速并得到广泛应用[16-17]。CPU和GPU能够容易地构成混合异构系统,利用传统消息传递模型、OpenMP编译制导和最新GPU编程接口CUDA可以实现混合并行算法,从而灵活处理具有不同并行特征的计算问题。由于MT Occam反演中存在的层次并行特征,本文采用异构混合并行方案来解决反演中不同粒度的并行计算,利用GPU与CPU的协同工作,实现系统整体计算能力的最大化。

3 混合并行方案设计

图1给出了混合并行模型框架,硬件自上向下分别是集群、节点和GPU计算设备,对应的软件环境为MPI,OpenMP和CUDA。

上层分布式并行模型MPI用于实现计算的节点间并行,本文采用全局静态通信,在映射过程中由主节点进程(主进程)负责对子节点进程(子进程)进行主动发送和接收,子进程被动接收和发送,在确认主进程接收前持续阻塞状态。图2给出了MPI层主进程的通信过程的实现代码,其中nproc为子进程数。

OpenMP层对上层发送的任务继续细分,并对GPU进行管理。反演的主要计算由GPU完成,节点CPU只负责少量的串行计算,因此没有设计利用CPU多核的算法来完成GPU之外的工作,加入OpenMP层的主要目的是为将来预留GPU扩展机制。

CUDA层负责完成有限单元法计算、矩阵叉乘、Chelosky分解等具有极细粒度重复计算特征的部分。主机端需要将计算数据拷贝至设备端显存,调用Kernel函数通过多线程方式完成并行处理,CPU最后将结果拷贝回内存。

图3为MT Occam CPU/GPU并行反演简化流程:主进程读入数据、对频率分组并分发数据到各子进程;子进程接收任务,调用GPU完成模型正演和雅可比矩阵计算;主进程接收子进程计算结果并对模型正演响应和雅可比矩阵进行汇总,调用GPU矩阵算法计算叉积矩阵,针对不同的μ值,调用GPU Cholesky分解算法计算相应模型并发送给子进程;子进程接收模型数据,调用GPU计算正演响应;主进程接收模型正演响应数据,计算其拟合差和粗糙度,评判模型,确定是进入下次迭代还是输出最终模型。

图1 CPU/GPU混合并行模型框架

图2 MPI层主进程通信代码

计算流程中正演响应和雅可比矩阵利用有限单元法计算,其线性方程组通过高斯消元法求解,此部分计算占比最大,是提高计算效率的核心部分。本文针对其系数矩阵的二维等带宽压缩存储结构和MT Occam反演的特点,设计了高斯消元GPU算法。算法以一个线性方程组的消元过程(一个工作三角形)为计算任务映射到CUDA模型的BLOCK线程块,然后由CUDA二次映射到流处理器上完成,总的映射任务数与节点计算频率数和GPU个数相关[18]。

叉积矩阵的求取和Cholesky分解计算量相对较小,不再分发到计算节点,而由主进程调用GPU单独完成。考虑到NVIDIA公司提供的函数库已经包含了部分高效算法,本文直接调用子程序cublasSsyrk_v2计算叉积矩阵,调用设备端函数cula_device_SPOSV实现Cholesky分解。

图3 MT Occam CPU/GPU并行反演简化流程

4 理论模型试算

本文采用的异构集群配置4个节点,每个节点配置1个物理4核i5-3470 CPU,8GB DDR3双通道内存,1个具有2GB显存的GTX 680 GPU(1536个流处理单元),节点间利用千兆局域网络连接。操作系统为CentOS 6.4,开发工具采用CDK,包含支持MPI,OpenMP和CUDA的C/C++和Fortran编译器,同时提供了性能分析工具和调试工具。

4.1 反演实验模型

为了评估算法的实际运行效率,本文实验过程中设计了5个模型,在所构建的异构集群上进行试算。每个模型均有2种采样规模(即类型1和类型2),限于文章篇幅,这里只展示2个典型模型及其反演结果,即模型1(类型1)、模型1(类型2)、模型2(类型1)和模型2(类型2)。2种采样规模的4项主要参数见表1,表中Nr为测点数,Nm为模型参量,Ne为有限单元网格数,Nf为观测频率数。最大反演次数定义为20。

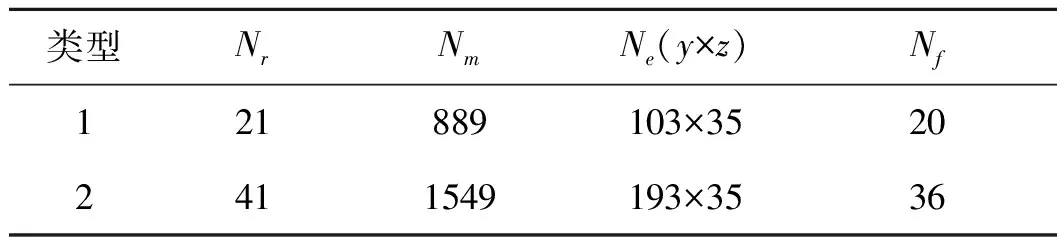
表1 理论模型参数

模型1(图4)设计为1000Ω·m基底,中部为相同电阻率的地垒,截面尺寸5.0km×12.5km,上部为100Ω·m均匀层。模型2(图5)设计为100Ω·m均匀半空间有2个不同电阻率棱镜体,上部为高阻层。

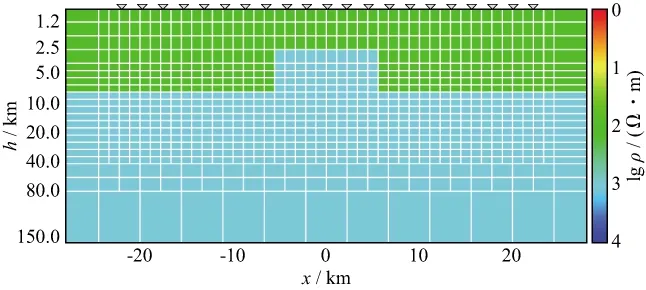
图4 反演模型1

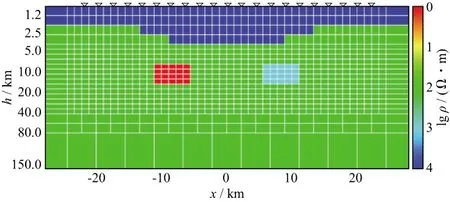
图5 反演模型2

类型1模型测点数为21,模型参量为889,有限单元网格数为103×35,观测频率数为20。类型2模型加密了各项参数,4项参数分别增加至41,1549,193×35和36。反演初始模型定义为100Ω·m均匀半空间,理论模型数据均加入5%的随机噪声。

4.2 算法测试结果

对类型1模型,分别用串行和并行算法计算5个模型的反演。定义偏差值为本次迭代串行算法所计算出的模型拟合差和粗糙度与相对应并行算法计算值之间差值的绝对值。图6给出了模型2反演过程中拟合差和粗造度的偏差值走势曲线,偏差值均不大,说明并行计算过程相对稳定。

表2给出了类型1和类型2模型串行算法和并行算法的迭代次数、计算时间和加速比的统计结果。结果表明,规模较大的模型(类型2)计算时间明显增多,但加速比也更大。个别模型出现正演次数的差异,分析原因是CPU与GPU处理器在浮点运算精度上的细微差异所致,最终反演结果没有受到影响。图7至图10展示了模型1和模型2两种规模下并行反演的结果(黑色实线为理论模型结构轮廓),对模型1来说,两种规模反演结果无太大差别,但从模型2的反演结果看,类型2与理论模型明显更为接近。

本混合并行方案反演结果正确,与纯消息传递方案相比,加速比有较大提升,说明方案合理可行。不同模型加速比有一定差异,这取决于模型规模、复杂度和映射到不同层次计算量的变化。总体而言,计算密度大的模型(如类型2)有着更大的加速比。在本文4节点环境下,类型1模型平均加速比为6.11,最高加速比为7.11,类型2模型平均加速比为16.46,最高加速比达23.49。

图6 模型2(类型1)误差曲线

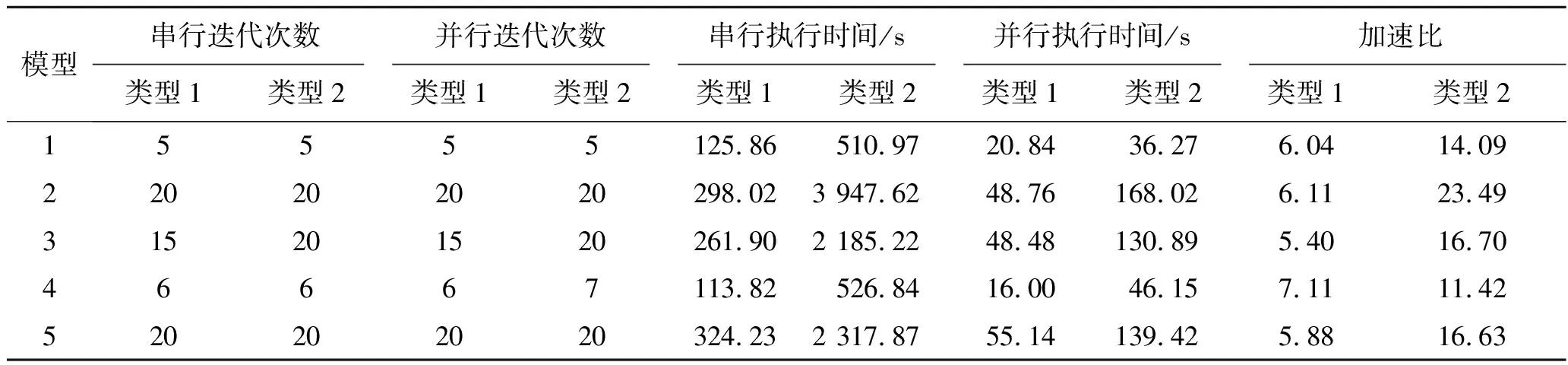
表2 理论模型反演统计表

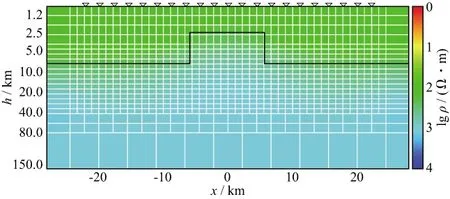
图7 模型1(类型1)反演结果

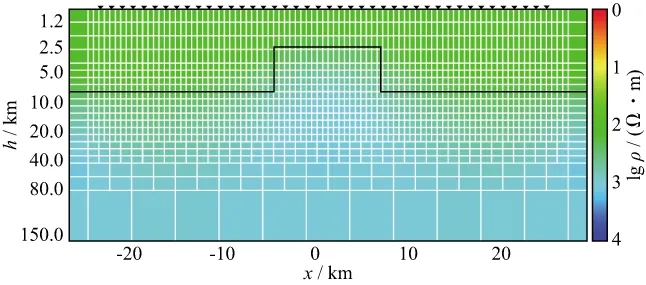
图8 模型1(类型2)反演结果

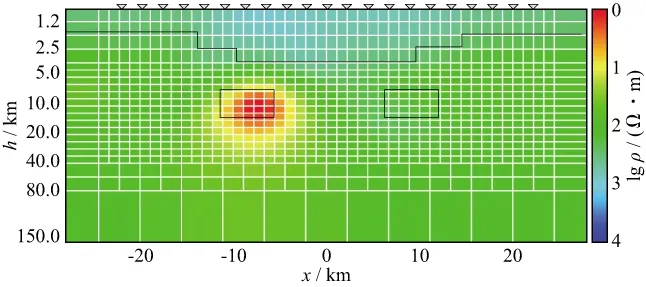
图9 模型2(类型1)反演结果

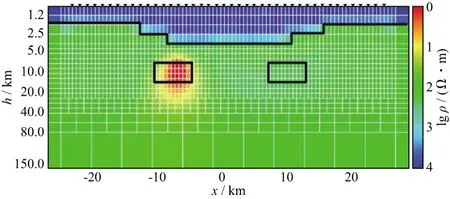
图10 模型2(类型2)反演结果

5 方案适用性分析

影响本文方案性能的因素主要源于两方面:①通信延迟。本文测试结果表明,混合模型各层均会造成一定的通信延迟。由于OpenMP层和CUDA层是共享内存方式,其延迟要远小于消息传递方式,因此,MPI层通信是主要的瓶颈。消息传递模型要求计算任务粒度尽可能大以提高通信效率,当模型较小特别是频点较少时(如类型1模型),本方案上层的任务粒度就相对较小,尽管在下层采用了GPU处理,整体计算性能仍会受到影响。②GPU计算并行度。方案中,反演过程的大量计算最终将映射到GPU的流处理器上完成,细粒度并行度便成为影响性能的因素。GPU计算要求一次将尽可能多的数据投入到运算中,当并行度不够时,流处理器(SP)资源不能得到充分利用,计算效率将会降低。由于上述2方面的影响,本文混合并行方案更适合于规模较大的模型(多测点、多频率、大密度网格)反演。

此外,系统存储性能制约了本文集群的适用范围。由于MT Occam反演对存储空间的需求较大,小规模集群通常适用于二维模型反演,测试结果表明本文设计的不同规模的多个二维模型反演完全可行。但就三维反演而言,由于有限单元节点数远远大于二维反演,其需要占用的存储空间是小型集群存储资源难以满足的,因此,如果要用于小规模三维模型反演,节点内存和GPU显存都必须增加,并对存储进行优化。

6 结论

MT Occam反演中传统的并行方法不具扩放性,计算性能的提升难以利用扩大集群规模的方式来实现。采用CPU/GPU多层次混合并行架构,通过挖掘细粒度并行分量,可以很好地弥补这一不足。线性方程组Gauss消元求解是反演过程中最为核心的计算,在GPU上实现其细粒度并行,能使极为耗时的雅可比矩阵和模型正演响应计算都得到加速,是提升反演速度的关键。矩阵叉乘、Cholesky分解也具有良好的细粒度并行性,并可直接利用CUDA并行函数库高效计算,这进一步提高了算法的综合计算性能。

本方案在4节点的小型集群上对较大模型(类型2)反演获得了平均16.46的加速比,最高达23.49,相对于纯消息传递方式有较大提高。较小模型(类型1)的反演受MPI层计算粒度和GPU层并行度的影响,平均加速比为6.11,最高为7.11,效率相对要低,但仍高于纯消息传递方式。混合并行模式下通信延迟是需要关注的问题,在我们的实验中,三层模型通信耗时最高达总计算时间的30%左右,说明数据通信已经成为本方案效率的主要制约因素,需要进行更多的优化,特别需要考虑计算与通信的重叠(overlap)。

致谢:感谢MT Occam 反演作者Steven Constable先生提供的串行源代码。

参 考 文 献

[1] 李小康.基于MPI的频率域航空电磁法有限元二维正演并行计算研究[D].北京:中国地质大学,2011

LI X K.A MPI based parallel calculation on two dimensional finite element modeling of AEM[D].Beijing:China University of Geosciences,2011

[2] 胡祥云,李焱,杨文采,等.大地电磁三维数据空间反演并行算法研究[J].地球物理学报,2012,55(12):3969-3978

HU X Y,LI Y,YANG W C,et al.Three-dimensional magnetotelluric parallel inversion algorithm using data space method[J].Chinese Journal of Geophysics,2012,55(12):3969-3978

[3] 吴小平,徐果明.大地电磁数据的Occam反演改进[J].地球物理学报,1998,41(4):547-554

WU X P,XU G M.Improvement of Occam’s inversion for MT data[J].Chinese Journal of Geophysics,1998,41(4):547-554

[4] SIRIPUNVARAPORN W,EGBERT G.An efficient data-subspace inversion method for 2-D magnetotelluric data[J].Geophysics,2000,65(3):791-803

[5] 陈小斌.大地电磁正反演新算法研究及资料处理与解释的可视化集成系统开发[D].北京:中国地震局地质研究所,2003

CHEN X B.New forward and inversion algorithms and a visual integrated system for MT data[D].Beijing:Institute of Geology,China Seismological Bureau,2003

[6] TAN H D,TONG T,LIN C H.The parallel 3D magnetotelluric forward modeling algorithm[J].Applied Geophysics,2006,3(4):197-202

[7] 刘羽,王家映,孟永良.基于PC机群的大地电磁Occam反演并行计算研究[J].石油物探,2006,45(3):311-315

LIU Y,WANG J Y,MENG Y L.PC cluster based magnetotelluric 2-D Occam’s inversion parallel calculation[J].Geophysical Prospecting for Petroleum,2006,45(3):311-315

[8] 刘羽.基于机群的二维大地电磁Occam反演的并行计算研究[D].武汉:中国地质大学,2006

LIU Y.PC-Cluster based parallel computation research on 2-D magnetotelluric occam inversion[D].Wuhan:China University of Geosciences,2006

[9] 陈露军.基于MPI的三维井地电磁场并行计算研究与实现[D].成都:成都理工大学,2006

CHEN L J.Research on parallel computation of 3-D borehole-surface EM based on MPI[D].Chengdu:Chengdu University of Technology,2006

[10] SIRIPUNVARAPORN W,EGBERT G.WSINV3D-MT:vertical magnetic field transfer function inversion and parallel implementation[J].Physics of the Earth and Planetary Interiors,2009,173(3/4):317-329

[11] 李焱,胡祥云,吴桂桔,等.基于MPI的二维大地电磁正演的并行计算[J].地震地质,2010,32(3):392-401

LI Y,HU X Y,WU G J,et al.Research of 1-D magnetotelluric parallel computation based on MPI[J].Seismology and Geology,2010,32(3):392-401

[12] CONSTABLE S C,PARKER R L,CONSTABLE C G.Occam’s inversion:a practical algorithm for generating smooth models from EM sounding data[J].Geophysics,1987,52(3):289-300

[13] GROOT-HEDLIN DE C,CONSTABLE S C.Occam’s inversion and the North American Central plains electrical anomaly[J].Journal of Geomagnetismc and Geoelectricity,1993,45(9):985-999

[14] 刘羽.MT Occam 并行反演方案及性能分析[J].武汉理工大学学报,2007,29(12):136-140

LIU Y.Parallel MT occam inversion scheme and its performance analysis[J].Journal of Wuhan University of Technology,2007,29(12):136-140

[15] 马召贵,赵改善,武港山,等.起伏地表叠前时间偏移的多级并行优化技术[J].石油物探,2013,52(3):280-287

MA Z G,ZHAO G S,WU G S,et al.Multi-level parallel optimization technique for prestack time migration from rugged topography[J].Geophysical Prospecting for Petroleum,2013,52(3):280-287

[16] JACOBSEN D A,SENOCAK I.Multi-level parallelism for incompressible flow computations on GPU clusters[J].Parallel Computing,2013,39(1):1-20

[17] 张猛,王华忠,任浩然,等.基于CPU/GPU异构平台的全波形反演及其实用化分析[J].石油物探,2014,53(4):461-467

ZHANG M,WANG H Z,REN H R,et al.Fall waveform inversion on the CPU/GPU heterogeneous platform and its application analysis[J].Geophysical Prospecting for Petroleum,2014,53(4):461-467

[18] XIAO Y,LIU Y.GPU acceleration for the gaussian elimination in magnetotelluric Occam inversion algorithm[J].Proceedings of the 4thInternational Conference on Computer Engineering and Networks,2015:123-131