矿井坑道音频电法超前探测模拟及其应用

骆 彬 张平松 胡雄武

(安徽理工大学地球与环境学院，安徽省淮南市，232001)

随着我国煤矿开采不断趋向深部，围绕煤层工作面开展的生产准备坑道在掘进过程中，常遭遇断层、陷落柱及岩溶等含导水地质构造，给煤矿生产安全造成了严重的水害威胁。目前，矿井直流电阻率法、矿井瞬变电磁法、矿井地质雷达和矿井地震波探测方法是超前预测上述含导水地质构造的主要技术手段。但经过大量实践，一些应用技术问题表现突出，如矿井直流电阻率法在数据采集时受现场地电干扰大，且电场随布极距离的增大而快速衰减；矿井瞬变电磁法易受掘进工作面周边金属类支护体的严重干扰；矿井地质雷达探测距离短且受金属干扰；矿井地震波对含水体的响灵敏度不够且现场探测施工程序繁琐等。以上问题导致这些方法在实际应用中存在数据采集质量低以及难以满足快速掘进生产需求的问题。为此，本文在矿井直流电阻率法的基础上，充分考虑其优缺点，提出矿井坑道音频电超前探测方法，拟通过建立坑道掘进前方含水断层的理论地电模型，分析视频散率的分布特征，并通过现场实践进一步检验该方法的可靠性。

1 音频电超前探测方法的理论基础

1978年Pelton利用Cole-Cole模型参数来描述岩矿石的激电特性。当供电电流较小时，岩石的激发极化效应可看作一个线性时不变系统，其频率域表达式为：

(1)

式中：R(ω)——复阻抗与频率ω相关的传递函数，Ω；

ΔU(ω)——输出复电位值，V；

I(ω)——供电强度，A。

在频率域电子导体与电解液界面上的复超电压可等效看作是单位面积上的复阻抗，于是构建一条等效电路便可模拟出电子导体与电解液界面上的阻抗，阻抗Zs表达式为：

(2)

式中： Zs(ω)——阻抗，Ω；

j——虚数；

ω——角频率，rad/s；

τ——时间常数；

c——频率相关系数。

如果将矿化岩石的一个基本结构单元简化成如图1(a)所示的结构，则可用如图1(b)所示的等效电路来模拟表示。

图1 矿化岩石某一结构单元示意图(a)和等效电路图(b)

依据Cole-Cole模型的阻抗表达式可得由岩石的激电效应引起的复电阻率的频谱表达式为：

(3)

式中：ρ(ω)——复电阻率与频率相关的传递函数，Ω·m；

ρ0——频率为零时的电阻率，Ω·m；

m——极化率。

2 含水断层的数值模拟

2.1 理论模型构建及电场方程求解

超前含水断层模型图如图2所示。假设含水断层均匀且沿走向无限延伸。

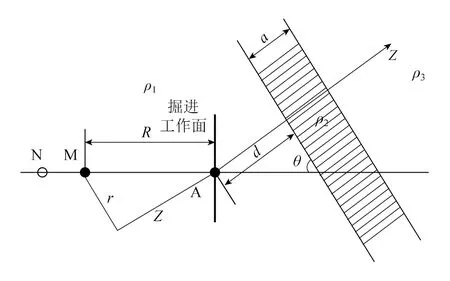
图2 超前含水断层模型图

以供电电源A为原点建立坐标系，其几何关系满足：

(4)

式中：r、z——自定义距离变量，m；

d——含水断层到供电点源A的垂直距离，m；

R——测量的异常电位距点电源距离，m；

θ——断层倾角，(°)。

且除A点以外空间内其他各点电位Ui(i=1，2，3)都满足拉普拉斯方程，可得断层靠点电源一侧岩层的中点位置P的电位为：

(5)

式中：U1——断层靠点电源一侧岩层的中点位置P的输出电位值，V；

I——供电强度，A；

ρ1——断层靠点电源一侧岩层电阻率，Ω·m；

a——断层厚度，m。

其中:

(6)

式中：Kij——自定义过程变量，i、j=1、2、3；

ρ2——含水断层电阻率，Ω·m；

ρ3——断层远离电源一侧岩层电阻率，Ω·m。

将式(3)代入式(5)，进一步可得：

(7)

式中：A(ω)、B(ω)——自定义过程函数。

则三极装置的视复电阻率的表达式为：

(8)

式中：AM、AN——分别为点电源到测量电极M和N的距离，m；

MN——测量电极M、N之间的距离，m。

进一步可得相应的视频散率(PFE)的表达式为：

(9)

2.2 模拟分析

令ρ1=ρ3=100 Ω·m，ρ2=10 Ω·m，η1=η3=0.1，η2=0.5，a=2.0 m，d=20 m，θ=60°，并取fG分别为1 Hz、10 Hz、100 Hz和1000 Hz，对应fL=fG/13。

不同供电频率条件下对应三极装置的视复电阻率分布曲线如图3所示。由图3可以看出，随着供电点A与测量电极MN的距离R增大，视复电阻率值逐渐下降，这是由于坑道掘进前方拟设含水断层所引起的；但供电频率不同时，视复电阻率曲线差异很大，总体表现出随供电频率升高，视复电阻率值减小，但曲线形态差异较小。

不同供电频率条件下对应三极装置的视频散率分布曲线如图4所示。由图4可以看出，随探测距离R增大，视频散率值逐渐递增，同样为含水断层所引起。但频率与视频散率之间的关系并非像与视复电阻率那样的单调关系，而是在频率为100 Hz附近时达到最大的视频散率，当频率过低(如f=1 Hz)或频率过高(如f=1000 Hz)，视频散率值均较小，说明利用音频电法超前探测时，应选择高频为100 Hz或其附近的频段，可获得较高的视频散率曲线。

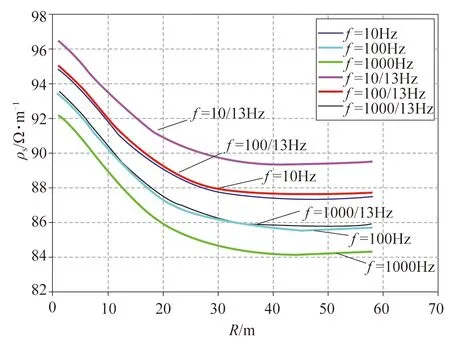
图3 不同频率的视复电阻率曲线

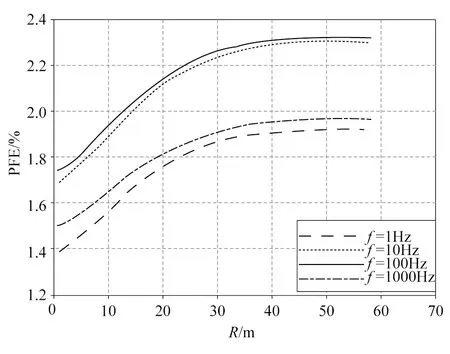
图4 不同频率的视频散率曲线

为了更好地分析超前含水断层的尺寸a、倾角θ及距离d等参数和PFE之间的关系，在上述假设参数的基础上，选择频率fG=100 Hz，除对需讨论的参数进行改变外，其他参数保持不变，分别计算相应的PFE数据。

不同断层倾角的视频散率曲线如图5所示。由图5可知，断层倾角的变换将引起视频散率值的大幅变化，如θ=10°和θ=90°对应的曲线极大值之间相差约0.3%；同时曲线的形态也出现明显的改变，在断层倾角较小时，曲线呈单峰形态，而当断层倾角较大时，曲线呈递增分布。

改变断层尺寸情况下的视频散率曲线如图6所示。由图6可知，随着断层尺寸的增大，视频散率值大幅上升，受含水断层的影响越大，电性异常越明显。

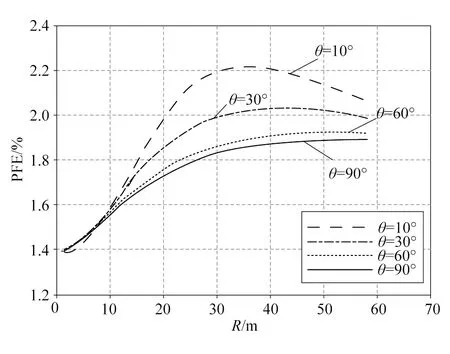
图5 不同断层倾角的视频散率曲线

图6 不同断层尺寸的视频散率曲线

改变断层与供电点距离情况下视频散率的分布曲线如图7所示。由图7可知，垂距d的改变将引起视频散率的幅值和分布形态的显著变化。d从小逐渐变大时，视频散率极大值逐渐减小，其对应的距离R逐渐增大，视频散率曲线从单峰逐渐变化为单调递增，反映含水断层随视频散率的影响逐渐增大，即电性异常变得更为显著。

综合以上分析可知，理论上而言，对于实际中不同断距、不同产状且与坑道掘进工作面不同距离的含水断层，采用音频电法进行超前探测时，其视频散率均表现出较为显著的电性异常，但异常特征会随上述参数的改变而表现不同。

图7 断层与点电源垂距不同的视频散率曲线

3 工程实践

淮北某矿回风上山坑道位于10号煤层底板，坑道顶板与10号煤层的法相距离为7～34 m，平均22 m。煤岩层总体为NW倾斜的单斜构造，其产状为8°～15°，倾角6°～15°，煤层厚度1.7～5.8 m，平均厚度3.8 m。坑道掘进施工过程中主要揭露粗砂岩、中砂岩、细砂岩。由于现有地质信息较少，其坑道掘进前方标高逐步降低，结合前期掘进资料，认为待掘坑道前方可能隐伏导水断层，存在相对高水压潜在危险。

为确保该坑道顺利安全掘进，巷道掘进过程中必须查明裂隙、断层等可能富水发育构造，防止巷道与水体导通。现场进行了音频电法超前探测试验。利用采集的128 Hz和16 Hz的视复电阻率数据计算视频散率，并按照文献中的方法进行视频散率偏移成像，获得音频电法的测试结果，如图8所示。由图8可以看出，在3次超前探测试验中共揭露了2个高频散区(即低阻异常区)，推断该段岩层裂隙发育且含水。经现场掘进揭露，2个高频散区均为岩层含水所致，在频散率变化区，部分为岩性变化，部分为岩层产状变化，局部为断层影响区。综合探采结果对比验证，可以确定本次音频电法超前探测结果是较可靠的，也进一步验证了该方法的有效性。

图8 现场音频电法探测成果图

4 结束语

随着我国煤层开采不断趋向深部，地质条件越加复杂，围绕煤层开采所进行的一系列坑道掘进均面临较大的安全威胁，其中水害是主要威胁之一。本文以音频电法理论为基础，提出音频电超前探测方法，通过对坑道掘进前方含水断层的视频散率公式的推导，模拟了视频散率与含水断层尺寸、倾角及位置等参数之间的变化关系，确定利用音频电法进行坑道掘进超前探测在理论上是可行的。通过现场的连续跟踪探测，进一步验证了该方法在解决实际问题的可靠性，能为煤矿防治水措施的制定提供技术支撑。

参考文献：

[1] 张玉军. 基于多源信息融合底板突水主控因素的定量化评价[J]. 煤矿开采，2017(2)

[2] 段中会，马丽，高阳等. 煤矿复杂地质条件精细预测预报技术及应用[J]. 中国煤炭地质，2017(9)

[3] 陈伟. 深部开采高承压岩溶水特征及突水性预测[D]. 安徽理工大学，2017

[4] 胡雄武，张平松，吴荣新等. 矿井多极供电电阻率法超前探测技术研究[J]. 地球物理学进展，2010(5)

[5] 胡雄武，张平松，严家平等. 坑道掘进瞬变电磁超前探水解释方法的改进研究[J]. 岩土工程学报， 2014(4)

[6] 段毅，许献磊. 地质雷达超前探测在常村煤矿的应用研究[J]. 中国矿业，2017(8)

[7] 王勃. 矿井地震全空间极化偏移成像技术研究 [D]. 中国矿业大学，2012

[8] 张金涛，周游，刘志民等. 超前探测巷道灾害性含导水构造的双频激电法[J]. 煤炭学报，2015(8)

[9] 胡雄武，张平松，程桦等. 井下瞬变电磁法超前探测中锚杆干扰定量评价[J]. 岩石力学与工程学报，2013(S2)