高速铁路站内绝缘节处轮轨接触阻抗研究
2018-05-31王晓明尚文斌尚文卿
王晓明,尚文斌,董 昱,尚文卿
(1.兰州理工大学电气工程与信息工程学院,兰州 730050; 2.兰州交通大学自动化与电气工程学院,兰州 730070;3.石家庄工程职业学院信息工程系,石家庄 050000)
我国高铁开通后,在京沪、沪宁、武广等线路均出现多起站内机械绝缘节和相邻钢轨间烧损现象,其中烧损现象最严重的大都发生在牵引回流切断点处;通常发生在侧线发车条件下,动车组前部和中部轮对经过绝缘节时,在轮轨接触位置可观测到放电拉弧现象,绝缘节被碳化烧损严重时会造成钢轨表面出现明显的坑洼[1-4]。
目前对绝缘节处电弧形成原因的理论分析研究相对较少,而本文提到的电接触理论多运用在分路电阻的计算研究中[5],因此本文基于国家自然基金项目中通过理论分析电弧模型成因,从而在绝缘节处设计特定灭弧装置,来从根本上解决绝缘节烧损现象这一研究课题,提出将电接触理论运用到轮轨在绝缘节处的接触电阻的计算及动态分析中,得出Mayr电弧模型的相关参数设计。为下一步分析电弧电流、电压并解决问题提供了必要前提。
1 接触电阻的理论分析基础
本文在计算接触电阻、建立轮轨动态接触数学模型中,运用基于点接触理论的轨道电路分路电阻计算方法研究中的电接触理论原理[5]。得到静态下普通线路的轮轨接触电阻计算公式如下
(1)
其中,
(2)

(3)
式中,Re为有污染膜层覆盖的导电斑接触电阻总和;Rp为无污染膜层覆盖的导电斑接触电阻总和;n表示导电斑的数目;ε表示有污染膜层的导电斑占总导电斑数的比率,ε=Se/Sr;Rme表示有膜层的导电斑互收缩电阻;Rmp表示无膜层的导电斑互收缩电阻;Rhi表示第i个导电斑的自收缩电阻;Rfi表示第i个导电斑上的膜层电阻。
2 建立轮轨动态接触模型
2.1 绝缘节处动态接触的分析及假设
在满足工程要求的前提下做出如下假设:
(1)假设所有导电斑在实在接触面积内是均匀分布的且半径均为α的圆形;
(2)视在接触斑视为半径为ra的圆形;
(3)轮对与钢轨的导电率ρ1=ρ2=ρ。
(4)
则
(5)

(6)
当λe=λ时,即轮轨间接触表面全部被污染层覆盖,此时接触电阻最大。切断点绝缘节处最可能出现电弧放电现象,本文主要在此情况下进行计算,此时接触电阻表达式如下
(7)
2.2 建立绝缘节处轮轨间实际接触面积的数学模型
在轮轨接触过程中,通过目前轮轨接触表面的大量的研究[6-16],车轮与钢轨的接触可以看成为二次曲面之间的接触。假设轮对完全与钢轨表面接触时,实际接触面积Sr的计算公式如(8)所示。
(8)
式中,H为轮轨材料的硬度。然而,当轮对经过绝缘节处时,由于轮对与绝缘节接触部分的接触斑不导电,因此实际接触面积Sr还会随着轮对继续运行而减小,此过程受列车运行速度的影响,所以用k表示钢轨上的视在接触面积Sg所占的总的视在接触面积比值。
由国际铁路联盟标准UIC510-5规定的载荷计算标准可知,车轮受到的纵向作用力由单个轮对所承载的质量Q决定,其公式如(9)所示。
(9)
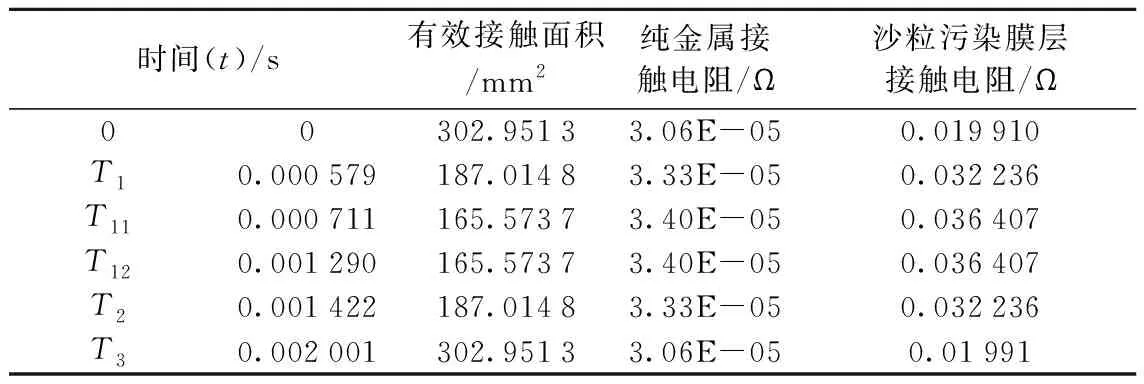
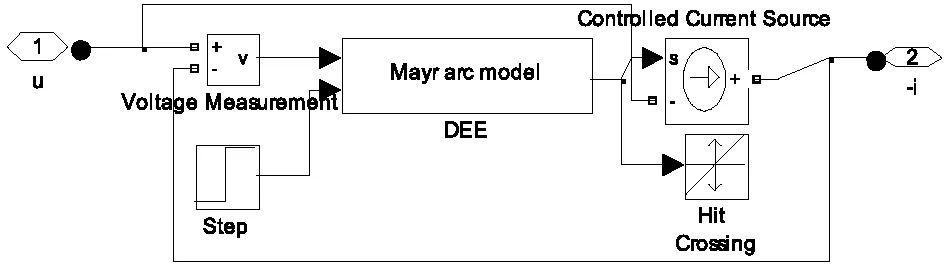
目前我国高铁绝缘节的宽度一般在6~10 mm,而根据文献[6]计算出的标准车轮和标准钢轨在对中位置处的接触斑面积为303 mm2,即视在圆形接触斑半径ra=9.82 mm。因此本文假设绝缘节的宽度d(d 图1 绝缘节处动态接触示意 其中,T1~T2时间内的动态接触示意如图2所示。 图2 T1~T2时间内绝缘节处动态接触示意 对模型中有效视在接触面积Sg的计算可建立如下所示的分段函数模型。 (10) 由式(4)、式(7)以及Sg的表达式可得接触电阻的计算表达式 (11) 本文以标准轮轨间的接触形式[6]为例,对无锡车站13号道岔[17]的切断点绝缘节处接触电阻进行动态分析计算,为研究绝缘节处烧损提供理论基础。相关参数以表1中为例进行Matlab程序设计,从而建立相关数学模型。 表1 相关参数 首先计算轮轨经由绝缘节时视在有效接触面积变化趋势。上文已经假设是在接触面半径为ra的圆形,在经过绝缘节时由于与绝缘节接触部分电阻近似为无穷大,所以需要计算圆形接触面与钢轨接触部分的面积变化情况。对上述数学模型求解得到的有效视在接触面积Sg的变化曲线如图3所示。 图3 有效视在接触面积的变化曲线 在计算接触电阻的过程中,考虑到污染膜层的不同腐蚀情况,考虑纯金属接触时,以及对不同电阻率的污染膜层完全覆盖时接触电阻大小的变化情况。图4为轮轨接触电阻动态变化曲线。 图4 轮轨间接触电阻的变化曲线 从图4可以看出,不同污染膜层下接触电阻差距很明显,尤其是沙粒污染膜层与纯金属接触的接触电阻在数量级上有明显的差距。 在实际站场绝缘节两点电位差的计算过程中,电阻计算要考虑到绝缘节前后轨道线路的距离差异,如图5中无锡站13号道岔所示绝缘节D处的电位差UD。 UD=UDAB-UDEB (12) 因此,需要计算出绝缘节前后分别加上钢轨电阻RDAB、RDEB后的电阻变化情况。经粗略计算可知RDAB=0.377 Ω,RDEB=0.315 Ω。 图5 无锡站13号道岔绝缘节示意 以污染膜层为氧化硅时为例分析一个分区所内,在机车第一个轮对经过前后电阻变化曲线如图6所示。 图6 绝缘节两端电阻的变化曲线 从图6可以看出,轮对在经过绝缘节这一短时间过程内绝缘节两端阻抗值发生了跳跃式变化,相应的电压也会有一个突变过程,从而容易产生电弧放电现象。 为了绝缘节两端电位差的计算需要,提取部分数据如表2所示。 表2 相关参数 根据表2数据可以得到图7中Mayr电弧模型的相关参数:时间常数tau=T3-T2=0.6×10-3s;在有污染膜层覆盖情况下,电弧电导的初始值为T2时刻接触电阻的倒数,即g(0)=31 s;电弧的初始冷却功率P0(0)与相应的牵引功率有关,本文拟设为1 000 W;电弧出现起始时间为T2,即t=1.4×10-3s。 图7 Mayr电弧模型 轮轨接触电阻,尤其是覆盖污染膜层后的接触电阻在轨道电路的相关计算中是不可忽略的一个参数,在电接触理论的基础上,提供了轮轨经由绝缘节这一动态过程中接触电阻的相对可靠、准确的计算理论与方法。通过建立数学模型,得到有效接触面的动态变化情况,同时考虑了不同污染情况对接触电阻大小的影响。 本文以无锡站为例分析计算了绝缘节两端电阻变化情况,为Mayr电弧模型的相关参数设计提供数据依据,为进一步进行绝缘节处电弧的仿真分析提供相应的理论基础,避免实际测量所面临的众多不便。 考虑不同站场复杂程度不一样,以及目前大多数站场已经投入运营的情况下,提出拟增设带通滤波器形式的自动灭弧装置来为牵引电流回流在绝缘节切断点处提供一个通路。即对轨道电路起到“一头堵”的作用,也不影响牵引电流回流的流通,从根本上避免发生电弧灼伤钢轨而产生的重大事故和经济损失。 [1] 杨世武,姜锡义,王星晖,等.高速铁路站内绝缘节和钢轨烧损模拟测试及研究[J].铁道学报,2013,35(10):82-88. [2] 田小丽.高速铁路站内轨道电路绝缘节烧损原因分析[J].铁道通信信号,2013,49(4):34-37. [3] 毕红军,丁志东,石先明,等.高铁站内绝缘节烧损解决方案[J].北京交通大学学报,2015,39(3):6-9. [4] 王智新,阳晋.京沪高铁电弧灼伤钢轨和绝缘节问题研究[J].铁路技术创新,2012(6):39-43. [5] 孙上鹏,赵会兵,陈德旺,等.基于电接触理论的轨道电路分路电阻计算方法研究[J].铁道学报,2014,36(3):31-36. [6] 神圣,张军,孙传喜,等.磨耗状态下机车车轮与曲线钢轨的接触分析[J].铁道学报,2012,34(6):15-19. [7] Rathod C, Wexler D, Chandra T, et al. Microstructural charac-terisation of railhead damage in insulated rail joints[C]. Materials Science Forum. Trans Tech Publications, 2012, 706: 2937-2942. [8] 陈泽深,王成国,王永菲.高速机车车辆动力学模拟中的轮轨接触模型[J].铁道机车车辆,2005(1):1-10. [9] 山本大輔,刘阳春.轮轨接触面形状与切向力特性的关系[J].国外铁道车辆,2014,51(6):40-43. [10] 肖乾,林凤涛,王成国,等.变摩擦系数条件下的轮轨滚动接触特性分析[J].铁道学报,2012,34(6):24-28. [11] 赵鑫,温泽峰,王衡禹,等.三维高速轮轨瞬态滚动接触有限元模型及其应用[J].机械工程学报,2013,49(18):1-7. [12] Vo KD,张茂帆.不同工作条件下交流、直流传动机车的接触应力、热量和磨耗对比[J].国外铁道机车与动车,2015(6):27-37. [13] 吴娜,曾京.高速车辆轮轨接触几何关系及车轮磨耗疲劳研究[J].中国铁道科学,2014,35(4):80-87. [14] 倪平涛.轮轨接触几何关系计算再研究[J].铁道机车车辆,2013,33(4):7-11,42. [15] 干锋,戴焕云,高浩.磨耗车轮踏面精确轮轨接触关系计算方法[J].交通运输工程学报,2014,14(3):43-51. [16] 高浩,戴焕云,倪平涛.考虑轮对弹性的轮轨接触点算法[J].铁道学报,2012,34(5):26-31. [17] 毕红军,赵幸,张敏慧.高铁站内绝缘节两端电位差的分析计算[J].北京交通大学学报,2013,37(5):151-156.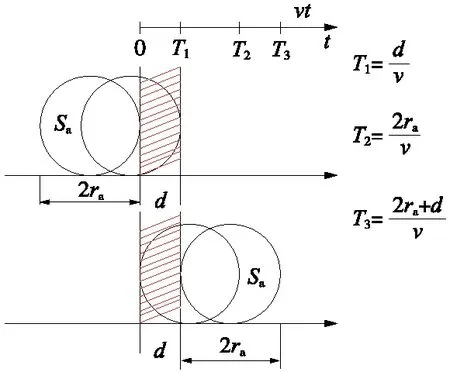
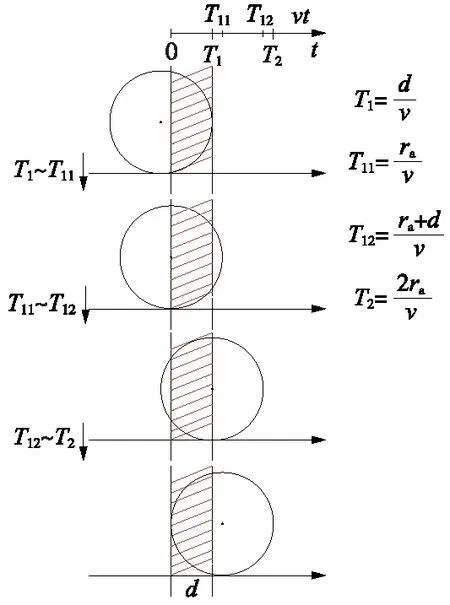
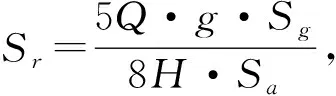
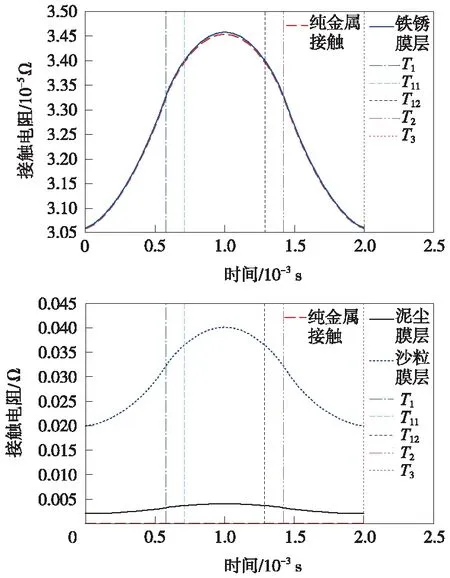
3 案例分析及数学模型求解




4 结语
