基于时间序列分析的无为县降水量预测模型的研究
2018-05-31奚立平蔡文庆吴海鹰
奚立平, 蔡文庆, 吴海鹰
(1.安徽水利水电职业技术学院,安徽 合肥 231603;2.无为县气象局,安徽 芜湖 238300)
无为县地处安徽省中南部,属亚热带季风气候区,旱涝频发,严重影响农业生产、社会经济发展等,因此利用时间序列分析法,建立降水量预测数学模型,服务于生活生产,尤其在防汛抗旱、农业生产等方面具有现实需求。
1 时间序列分析原理
降水是随时间变化的,对其观测形成一组有序的数据,称为时间序列,从“时域”角度对降水进行分析,称为时间序列分析,其基本思想是认为降水在随时间变化过程中任一时刻的变化和前期降水变化有关,利用这种关系建立适当的模型来描述它们变化的规律性,然后利用所建立的模型做出降水未来时刻的预报值估计。平稳时间序列模型主要有3种。
(1)自回归模型AR(p)。
Xt=φ1Xt-1+φ2Xt-2+…+φpXt-p+at
(1)
其中,p为模型的自回归阶数;Xt为平稳、正态、零均值的时间序列;φ为不为零的模型系数,表示时间序列中要素前后时刻间相关性大小;at为白噪声序列。
(2)移动平均模型MA(q)。
Xt=at-θ1at-1-θ2at-2-…-θqat-q
(2)
其中,q为模型的移动平均阶数;Xt为平稳、正态、零均值的时间序列;θ为不为零的模型系数,表示时间序列中要素与前期时刻白噪声间相关性大小;at为白噪声序列。
(3)自回归移动平均模型ARMA(p,q)。
Xt=φ1Xt-1+φ2Xt-2+…+φpXt-p+at-θ1at-1-θ2at-2-…-θqat-q
(3)
自回归移动平均模型ARMA(p,q)可以看成是自回归模型AR(p)的发展,即用p阶自回归模型AR(p)描述Xt所余下无法拟合的部分,用q阶移动平均模型MA(q)来描述。
2 降水量时间序列模型的建立及预测
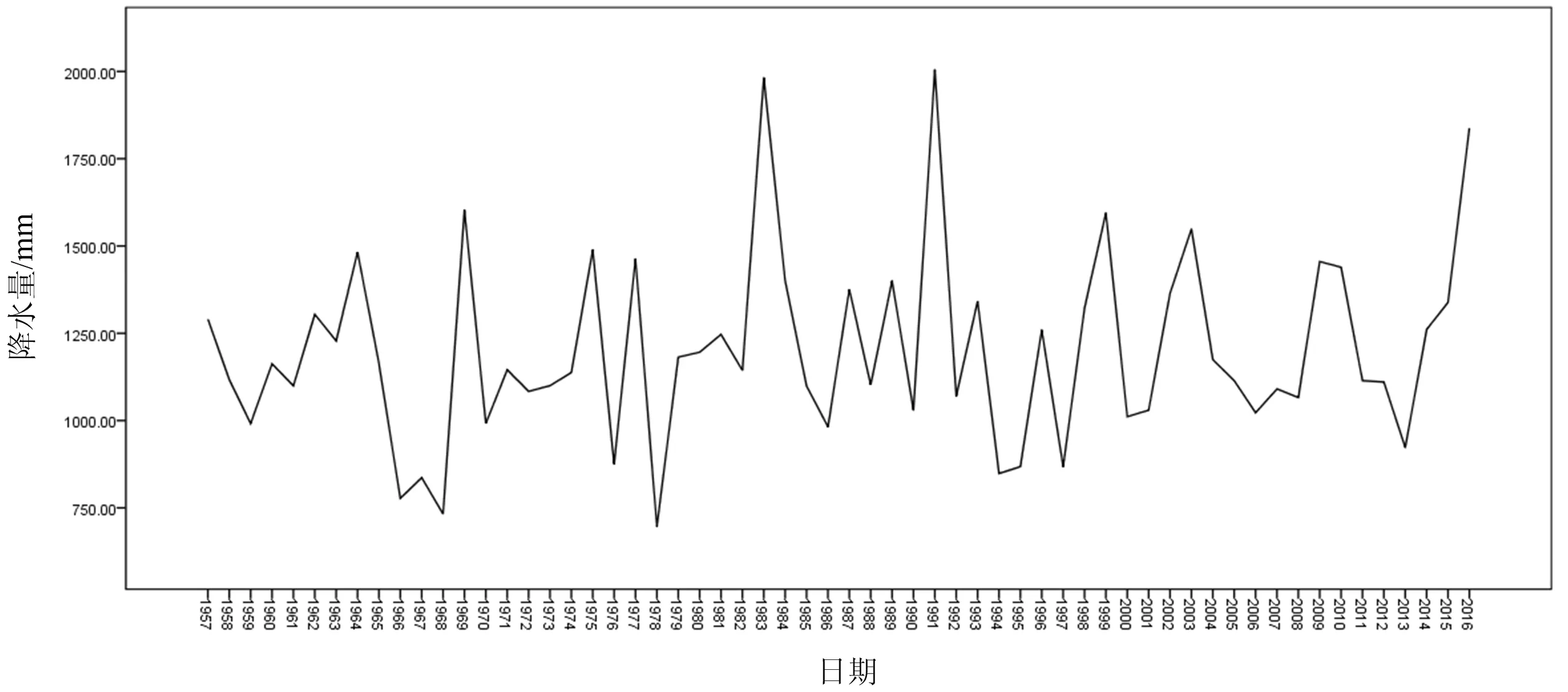
图1 无为县年降水量序列图

图2 无为县年降水量自相关系数图
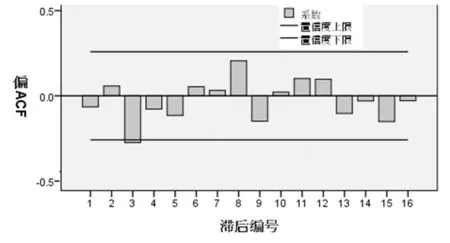
图3 无为县年降水量偏自相关系数图
利用spss 23统计软件,输入无为县1957~2016年年降水量资料,其序列图如图1所示,显然是平稳序列。
进一步对自相关性和偏自相关性进行检验,结果如图2、图3所示,由图可知,无为县年降水量序列接近于白噪声序列,反映无为县年降水量随机性强。
对序列进行1阶和2阶差分处理,其相关性仍然较弱难以建模。
为了增强序列的相关性,对降水量进行5年叠加,1957~1961年的降水量叠加作为新序列的第1个值,1958~1962年的降水量叠加作为新序列的第2个值,以此类推,得到5年叠加后的新序列,对自相关性和偏自相关性进行检验,结果如图4、图5所示,由图可知,新序列是平稳非白噪声序列。
由图4、图5可见,自相关系数在K=2之后基本都落在2倍标准差范围内,可判断其为自相关系数2阶截尾,偏自相关系数在K=1后基本上落入2倍标准差范围以内,可以判断其偏自相关系数1阶截尾,而自相关系数、偏自相关系数开始逐渐变化,且后边还有接近甚至稍大于2倍标准差的,故也可以判断其拖尾,因此,可采用MA(2)、AR(1)以及ARMA(1,2)分别进行拟合。
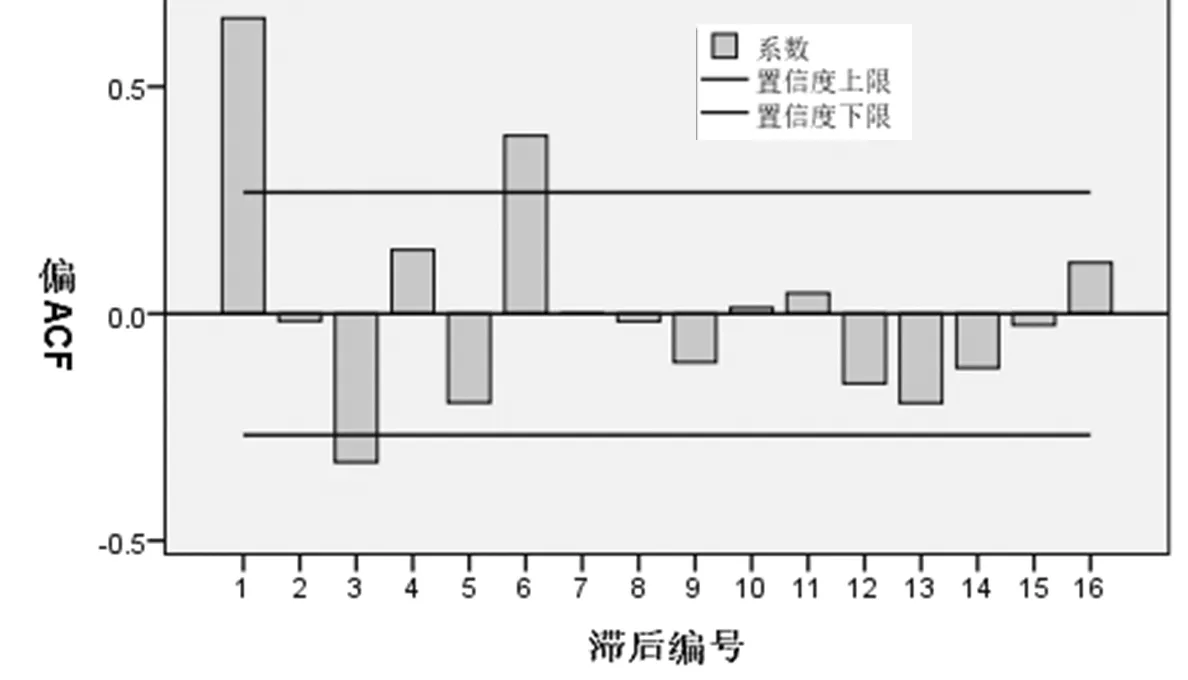
图5 无为县5年叠加降水量偏自相关系数图
尝试建立MA(2)模型,从模型统计量表1可知,平稳的R2=0.493,杨-博克斯统计量为32.520,伴随概率小于0.05,反映拟合模型的残差存在相关性,不为纯随机序列,从自相关图和偏自相关图如图6所示也能看出这一点,因此,采用MA(2)建模效果较差。

表1 MA(2)模型统计量
再尝试建立AR(1)模型,从模型统计量表2、自相关图和偏自相关图(图7)可得出与上述相似的结论,因此,采用AR(1)建模效果也较差。

表2 AR(1)模型统计量
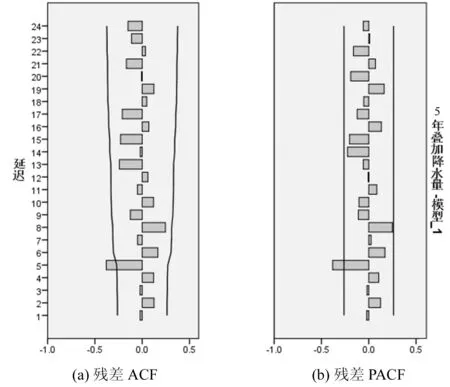
图6无为县5年叠加降水量MA(2)自相关系数与偏自相关系数图

图7 无为县五年叠加降水量AR(1)自相关系数与偏自相关系数图
最后,尝试建立ARMA(1,2)模型,模型参数如表3所列,经过t检验,自回归系数的伴随概率均小于0.05,显著非零,有统计学意义。从模型统计量表4可知,平稳的R2=0.563,杨-博克斯统计量为22.375,伴随概率大于0.05,再结合从自相关图和偏自相关图(图8)来看,反映拟合模型的残差项不存在相关性,残差序列为白噪声序列,另外,采用ARMA(1,2)拟合的模型不存在离群值,模型的拟合度较好。

表3 ARMA(1,2)模型参数

表4 ARMA(1,2)模型统计量
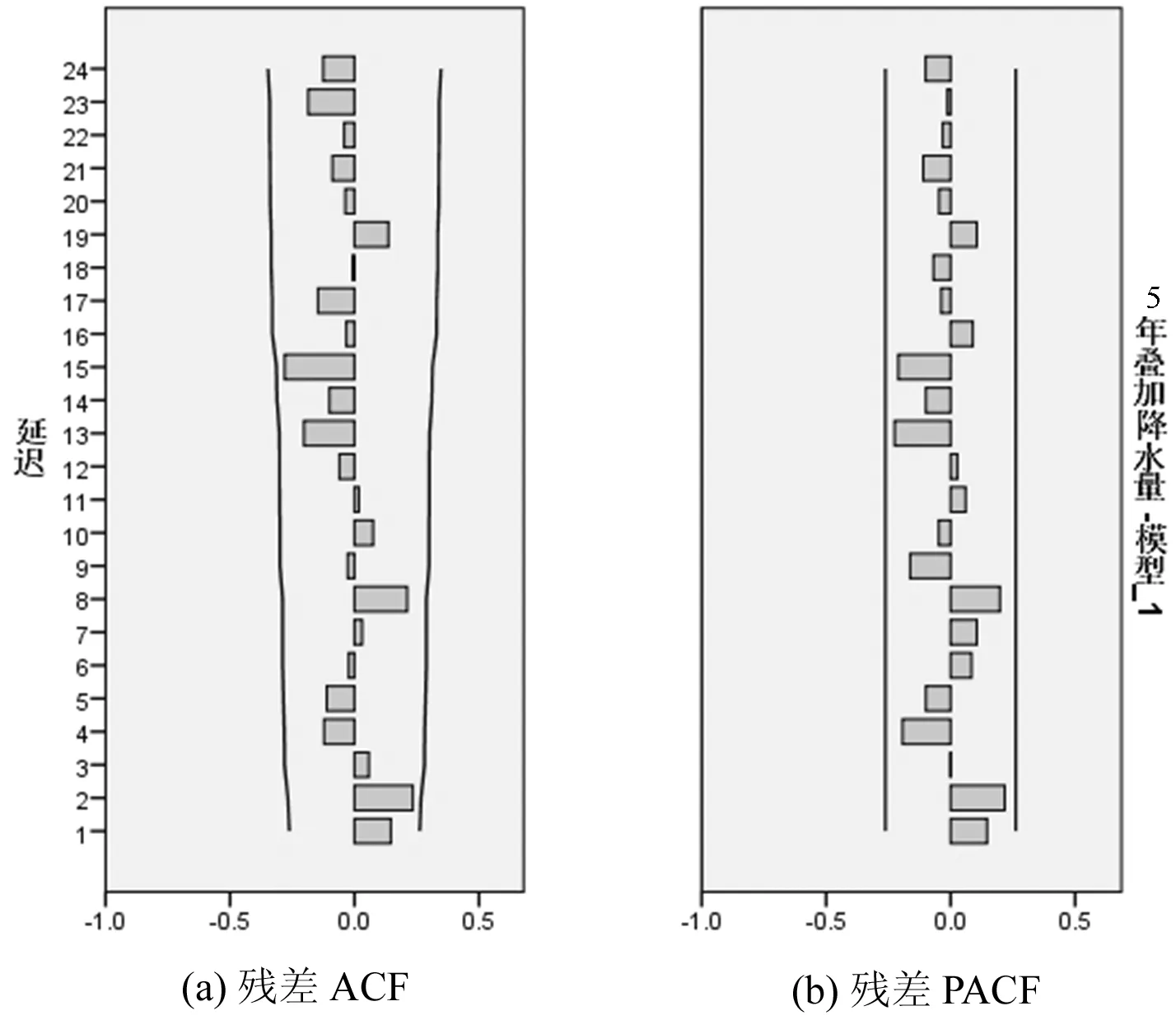
图8无为县5年叠加降水量ARMA(1,2)自相关系数与偏自相关系数图
综上可知,拟合的模型为:
Xt=-0.742Xt-1+at+1.608at-1+0.963at-2
(4)
利用上述模型对时间序列进行模拟,用拟合值与5年叠加的实测值进行对比,结果如图9所示。
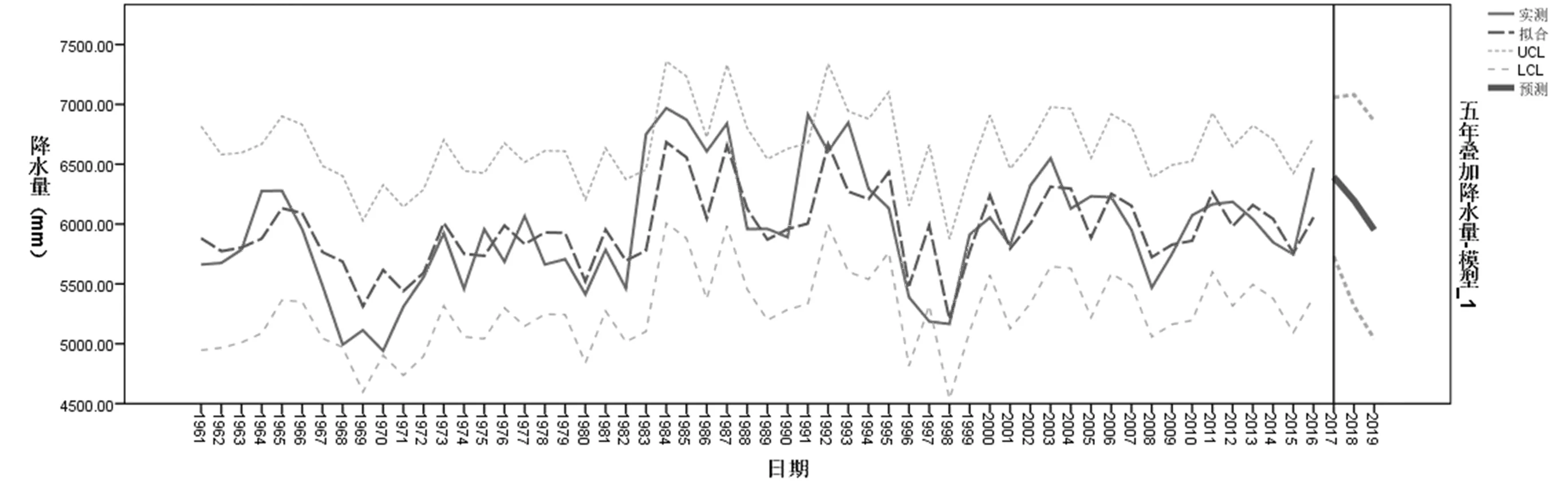
图9 无为县5年叠加降水量采用ARMA(1,2)模型拟合值与实测值对比图
由图9可见,拟合的最大相对误差约为11.3%,最近2年(2015、2016)的拟合值与实测值对比如表5所列,其相对误差分别为0.30%和-6.53%,说明模型精度较高,拟合效果良好。
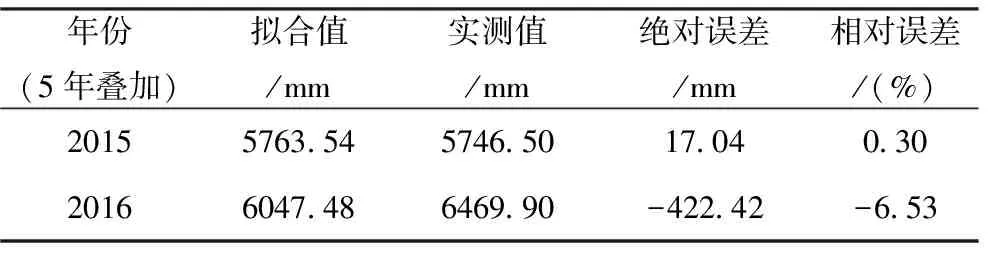
表5 2015、2016年5年叠加降水量的拟合值与实测值比较

表6 5年叠加降水量预测
利用模型对未来的值进行预测,2017、2018、2019年的预测值如表6所列。2017年至2019年的叠加降水量呈下降趋势。需要说明的是,由于分析的序列是5年降水的叠加值,所以拟合模型计算出的预测值不是某一年的降水量,而是5年累计的降水量。
3 结 论
由于无为县降水量随机性强,相关性弱,即使进行1阶和2阶差分处理,其相关性仍然较弱,因此采用五年叠加的方法增强序列的相关性,得到平稳的新序列。
根据自相关系数、偏自相关系数判断,新序列可能存在MA(2)、AR(1)以及ARMA(1,2)3种模型。其中MA(2)和AR(1)模型的伴随概率均小于0.05,从自相关图和偏自相关图,可以看出2种模型的残差序列为非白噪声序列,不采用。ARMA(1,2)模型的拟合度较好、符合要求,是选定的模型。
ARMA(1,2)模型的预测表明,无为县5年叠加降水量自2017年至2019年处于下降通道。
[参考文献]
[1] 孙明玺,吴俊卿,张志兴,等.实用预测方法与案例分析[M].北京:科学技术文献出版社,1993.
[2] 黄嘉佑.气象统计分析与预报方法(第4版)[M].北京:气象出版社,2016.
[3] 薛冬梅. ARIMA模型及其在时间序列分析中的应用[J].吉林化工学院学报,2010,(3):80-83.
[4] 何延治.基于时间序列分析的吉林省粮食产量预测模型[J].江苏农业科学,2014,(10):478-479.
