航道内船舶安全距离计算模型研究

刘 超

(安徽交通职业技术学院，安徽 合肥 230051)

航道内船舶安全距离计算是船舶在航期间需考虑的一个重要的基础性数据。在单项航道内行驶船舶,在假设航道顺直,航道长度不会限制船舶的正常航行,设定航道水深满足所有船舶正常通航,不需候潮等待,仅允许同向航行,禁止船舶在航道内进行追越活动的情况下,引入交通流理论与船舶领域概念,建立理想情况下航道内船舶最小安全间距计算模型,并对模型通过能力进行分析, 可作为船舶航行操作方式比选,航道规划、设计,航运交通管理及控制方式等参考的依据。

1 航道内船舶最小安全间距计算模型假设

船舶交通系统运行过程主要包含航道条件和船舶交通流状态两部分。在构建航道内船舶最小安全间距计算模型时,为描述问题和分析问题的方便,本模型做了一些优化和假设。其主要由航道模型和交通流模型两部分构成,具体描述如下:

航道假设条件包括航道长度、宽度、水深、弯曲半径以及潮汐等。考虑到本文的主要研究对象为非追越航道,因此对航道模型进行简化。首先,航道作顺直化处理,不存在转弯或航道交汇情况。其次,假设航道长度不会限制船舶的正常航行,同时设定航道水深满足所有船舶正常通航,不需候潮等待。最后,假定船舶在航道模型中仅允许同向航行,同时禁止船舶在航道内进行追越活动。

船舶交通流是指某水域内所有船舶运行的表现形式。船舶交通流的主要评估参数有速度、密度、到达率、船舶间距等。通常,对于交通流的评估和计算可以直观地体现出所在航道的船舶航行状态和通航情况。在这里,结合单向航道的特点,还需要考虑船舶领域在船舶局面判断中的作用。船舶领域是指船舶在航行过程中,为保证通航安全,禁止其他船舶进入的水域。安全领域的确定通常与船舶所处环境,船舶自身状况,以及航行规则有紧密联系。正由于本模型模拟航行环境仅考虑单一航向非追越航道,在确保水深条件下,船舶处于尾随状态航行,在航道内无追越和对遇局面,故无需考虑船舶左右领域安全。因此重点需要考虑船舶前后安全距离作为船舶避免碰撞局面的主要参考因素。

2 航道通过能力计算模型构建

根据航道内船舶前后安全间距的概念,与前后船舶速度差ΔV,进入时间间隔T,前船速度V及航道长度L有关。即D=f(L,V,T)。本文从船舶交通流微观特征,即船舶间函数关系角度确定最终理论运算公式。

2.1 理想情况下航道通过能力

航道理论最小安全距离,是指航道条件和交通状况都处于理想状态下,船舶在一定时间间隔下连续驶入, 其前后船舶需保持的最小安全距离[4]。在这种情况下, 航道中的船舶彼此间没有超越机会, 只能尾随行驶,直至驶出航道。以下结合航道理论通过能力,对理想状态下航道通过能力进行了分析。

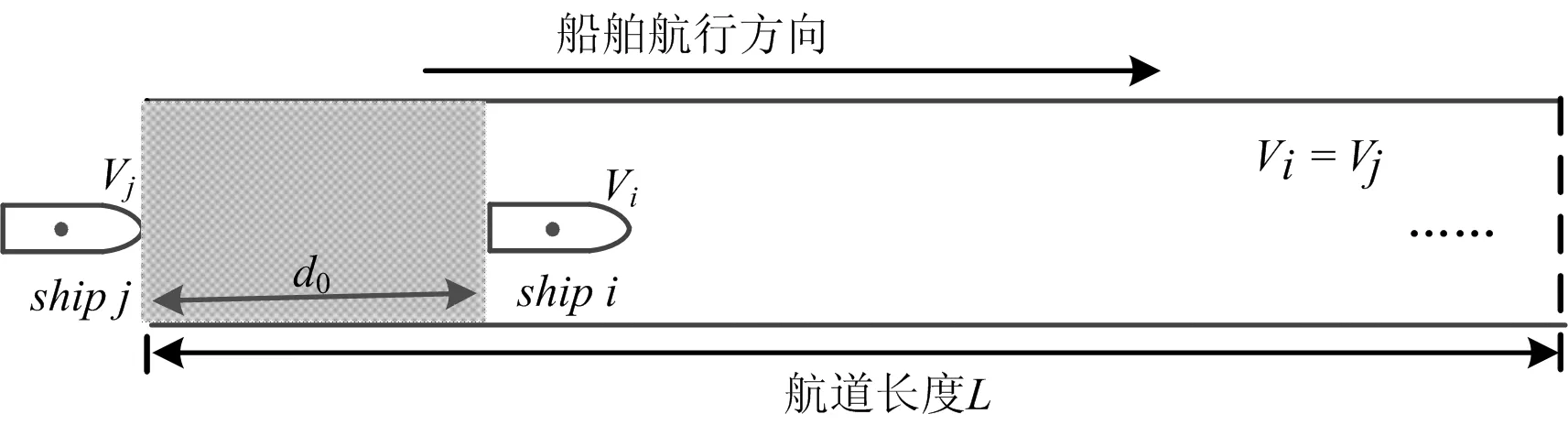
图1 理想情况下航道通过能力分析示意图

在图1所示情况下,相邻的两艘船舶构成了一个基本的单元组。设前后船舶间隔时间T驶入航道。为保证航行安全,其时间间隔至少需满足T×V≥d0。当前船Si与航道端口的距离达到最小安全间距d0时,后船Sj进入航道。因此,在保证前后船舶满足最小安全间距连续驶入的前提下,船舶驶入航道时间间隔、安全距离和设定的船舶速度构成函数关系。函数关系为:

(1)

其中,t为时间变量,每达到时间间隔Tij,后续船舶便可进入航道式(1)中,d0和V的单位分别用m和m/s表示。

2.2 模型通过能力分析

船舶到达航道时的速度差异是客观存在的,前后船舶速度差异对航道通过能力有直接的影响。当后序船舶速度小于前序船舶时,两船空间距离便随时间累积而逐渐增大,船舶在航行状态可时刻满足最小安全距离;当后序船舶速度大于前序船舶速度时,空间距离随时间累积而逐渐减小,可能缩小至安全间距以内,从而威胁船舶航行安全。

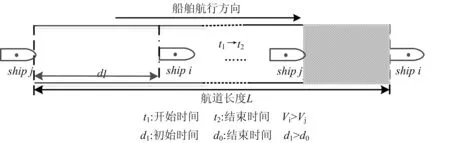
图2 速度差异下的船舶间距变化分析

如图2所示,当前船速度Vi小于后船速度Vj时,为保证船舶Si、Sj从进入航道直至驶出过程中,前后船距离始终大于等于最小安全距离d0,故相邻船舶进入航道的初始间距d1要重新设置。在前后船舶最小安全间距得到保证的情况下,每艘船都能维持船舶匀速航行状态。d1的大小可通过两艘船舶的速度和航道长度推导出来,即

t=L/V1

(2)

当前船速度大于或等于后船速度时,相邻船舶进入航道的初始间距可取最小安全间距d0。

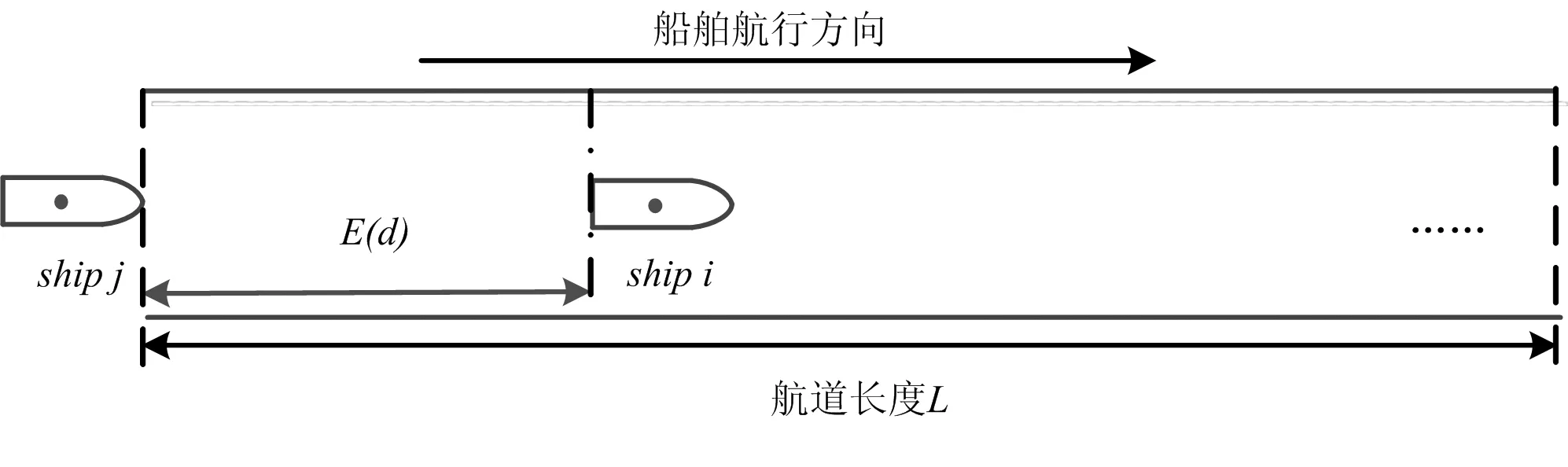
图3 结合船舶速度差异的航道通过能力分析

图3是将为相邻船舶进入航道的初始间距。当前船与航道端口的间距为E(d)时,后船可以进入航道。之后后续交通流依次按此间隔进入航道。结合公式(2)～(3),在考虑船舶速度差异影响的情况下,航道前后船舶安全距离如下表示:

(3)

在一定通航环境情况下,船舶进入航道的初始速度值趋于某一值μ,但又有所差异,交通流内船舶的船速基本服从正态分布情况。假设船舶到达航道入口的初始速度服从均值为μ,方差为σ2的正态分布,即V～N(μ,σ2)。当σ越大,相邻船舶速度差P2×(Vj-Vi)较大的可能性越大。同理,当σ越小,相邻船舶速度差L×(V1±ΔV)较大的可能性越小。可见,与L×(V1±ΔV)与σ成一定的相关性。经化简后,航道通过能力的公式可表示为:

(4)

其中,航道船舶最小安全距离D受交通流内船舶平均速度μ、速度标准差σ、航道长度L、及船舶进入航道间隔影响。

3 仿真实验分析

通过设计仿真场景,进行了一系列仿真实验,并进一步探讨和验证了该部分的计算模型。通过对仿真结果的分析,可以看出计算模型在一定程度上是合理的。

仿真模型分为两部分:船舶模型和航道环境模型。航道模型包括航道生成模块、航道运动模块和航道决策模块3个子模块。在航道生成模块中,需要考虑航道到达规律和航道间隔等参数。通过输入真实船舶交通流量进行统计分析。船舶运动模块主要用于显示船舶在航道中的航行性能。最后利用船舶决策模型的工作机制,对实时区间和最小安全距离进行了比较。航道模型的设计主要通过建立外部参数,如航道状况和水文条件的限制,船舶导航。除了在之前模型假设中提出的一些条件外,船舶交通流模型假设如下:① 每个船舶都被单独认为是一个对象,除航道间隔要求外,无其他干扰;② 在通道中,船舶的运动只在一维模型中进行,且船舶沿交通流方向直线运动;③ 一旦船舶速度的变化,变化是瞬间完成,减速后,前后船舶速度一致。

基于此假设建立模拟情景,经过实验发现最小安全距离变化与以下5个参数有关:通道长度L,船舶最大通过能力,平均速度v、速度标准差σ航道到达率λ。在通道环境设计中,平均速度v和船舶最大通过能力被视为2个显著常数,其余参数为变量。在每一次仿真试验中,采用Mont Carlo仿真方法,通过改变船舶最大通过能力,得出船舶最小安全间距的计算指标。假定的平均速度约为10节,标准偏差为插在范围从1节到3.7节。由此发现当d超过一固定值C时,航道内船舶通过能力将明显下降。故在实验中,设定C取值范围变化并进行4个样本研究,如表3所列。

表3 实验数据设计

当减速船只的数量在1天内达到80%时，每艘船舶的备用时间将显著增加，航道将过于拥挤。在保证船舶间距高于船舶最小安全距离的情况下，每天减速船只的数量的80%时的阀值可以作为其船舶通航安全间距的测算标准。

4 结束语

本文根据船舶交通流的特点和船舶的船舶干扰分析，提出了航道安全距离的计算模型。并同时设计了1组仿真实验，验证了计算模型的合理性。结果表明，计算模型的数据在一定程度上与仿真数据相吻合。同时，计算模型清晰地反映了航道内船舶间距与航道流速、航道长度等因素的关系。因此，在对于1个特定的航道进行设计规划时，可以通过数据采集和概率统计分析船只速度的特性。在此基础上，结合仿真拟合得到计算模型内部相应参数。这对航道安全间距的计算具有重要的理论指导意义。该理论模型的提出可为相关部门确定速度限制标准，提高管理水平提供一定的科学依据和决策支持。

[参考文献]

[1] 吴兆麟.海上交通工程概述[M].大连:大连海运学院出版社，1986.

[2] Fuji J and Tanaka K. Traffic capacity [J].Navigation，1971,(24):543-552.

[3] Goodwin EM. A statistical study of ship domains [J ].Navigation，1975, (28): 329-341.

[4] 董宇,姜晔,何良德.内河航道通过能力计算方法研究[J]. 水运工程,2007,(1):59-65.