无线可充电传感器网络中充电器的部署优化

王志方,郑 霖,李晓记

(1.桂林电子科技大学 信息与通信学院,广西 桂林 541004; 2.广西信息科学实验中心,广西 桂林 541004)

0 概述

无线传感器网络(Wireless Sensor Network,WSN)由部署在监测区域内的大量传感器节点和一些汇聚节点组成,是通过无线通信方式形成的多跳自组织网络系统。在WSN中,传感器节点协作地感知、采集和处理网络覆盖区域中被感知对象的信息,并发送给观察者[1-2],其中传感器节点由有限的一次性电池供电且很难更换电池[3],这使得WSN的生命周期受到影响,严重制约其发展。文献[4]在实验中采用磁谐振耦合的技术验证了无线能量传输的可行性,这为WSN中传感器节点的能量补充提供了一个解决方案。

由无线充电器充电的无线传感器网络也称为无线可充电传感器网络(Wireless Rechargeable Sensor Network,WRSN)[5-6]。WRSN中一个关键问题是无线充电器的部署问题。无线充电器很昂贵[7],并且它们的部署需要花费很多的时间和成本,如何有效地部署无线充电器,使得网络的充电代价最小化,是一个亟待解决的问题。

目前针对WRSN的研究多数为对移动充电策略的研究[8-9],而对固定天线充电器部署问题的研究并不多见。文献[10]研究在室内的环境下如何部署配有定向天线的无线充电器,使得无线充电器覆盖全部传感器节点,并提出了基于节点的贪心锥选择算法和基于对的贪心锥选择算法。文献[11]提出一种基于自适应对的贪心锥选择(APB-GCS)算法,通过迭代以贪婪地选择覆盖大多数传感器的充电器。文献[12]中假设充电器网络的布置为等边三角形,通过研究点配置和路径配置这两种形式,使用最少数量的充电器来确保放置在网络任何位置的静止或移动的标签可以获得足够的功率用于持续正常工作。文献[13]考虑数据汇点对传感器的影响,提出一种能够减少所需定向充电器数量并仍然保持良好充电效果的功率平衡感知部署方法。

上述针对无线充电器部署的研究忽略了节点的位置关系和拓扑特征,传感器节点随机地分布在指定区域中,会造成传感器节点的密度不均匀,使得充电器的数目增多。为此,本文定义室内随机非均匀环境下WSN的充电覆盖问题,寻找最少数量的固定无线充电器,其中充电器位于网格顶点处,且充电器的覆盖区域被假设为圆形。为部署传感器节点非均匀分布下最少数目的充电器,根据文献[14-15]的启发,将节点的位置关系和拓扑特征考虑到充电器的选择中,提出利用分割技术和移位策略的近似算法,并结合最小包围圆算法,设计基于k-中心点算法的聚类分区算法。

1 WSN网络模型和问题

如图1所示,给定一个无线可充电传感器网络,其中传感器节点随机的部署在长为L、宽为W的长方形区域内,负责为传感器节点进行充电的充电器位于距离长方形H的高度处。如图2所示,无线充电器配备有3D波束成形定向天线。当传感器节点位于无线充电器的充电圆锥内,即传感器节点位于无线充电器的覆盖范围内,假定传感器节点可以接收到无线充电器传输的能量。

图1 无线可充电传感器网络示意图

图2 无线充电器覆盖模型

充电范围R是指在无线充电器的范围内使得在传感器节点的功率接收率至少超过一个阈值δ,这里传感器节点i的功率接收率用Ui表示。Ui是与距离有关的参数,随着节点i与无线充电器的距离增大而减小,当传感器节点i与无线充电器的距离大于r0,此处假定其功率接收率过低,使得传感器节点的电池磁谐振耦合无法正常工作。rij为传感器节点i到无线充电器j的距离,当rij≤r0时,节点i的功率接收率Ui=μ(rij)×UFull,否则Ui=0。这里UFull是无线充电汽车(Wireless Charging Vehicle,WCV)为单个传感器节点满功率输出,μ(rij)为无线功率传输的效率,μ(rij)是关于rij的减函数,且0≤μ(rij)≤1。本文旨在使用最少数量的无线充电器对平面中的所有传感器节点进行充电,该问题定义如下:

问题1给定位于欧几里得平面U的目标传感器节点,寻找到最少数目的充电器,使得充电器能覆盖全部的传感器节点,并且每个传感器节点至少被无线充电器覆盖一次。

2 算法设计

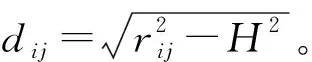
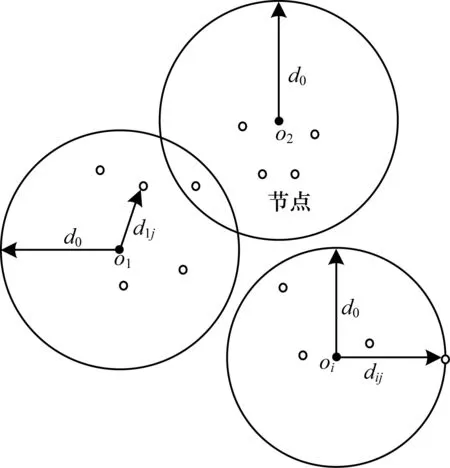
图3 无线充电器充电范围

2.1 近似算法

假设Q是覆盖N中所有点的正方形。用于问题1的分割技术的思想如下:首先将正方形Q划分为称为单元的正方形网格,每个大小为m×m,其中m为常数(见图4);然后解决每个单元的问题1;最后将所有单元的解的联合作为对原始输入的解[16]。

图4 m×m正方形网格

近似算法的具体步骤如下:

步骤1将平面U划分成正方形,边长皆为m(m>2d0),集合Q=F1∪F2∪…∪Fu,其中Fi表示有节点存在的正方形,u为节点存在的正方形的数目。

步骤2对任一集合Fi,寻找单元格中最少数目的充电器Fi(c)。

步骤3输出Q=∪Fi(c)。

因此,在所有非空单元格中,算法总时间为:

(1)

所有目标传感器节点随机分布在平面U上。本文通过移位策略,移动单元格以减少充电器的数目。

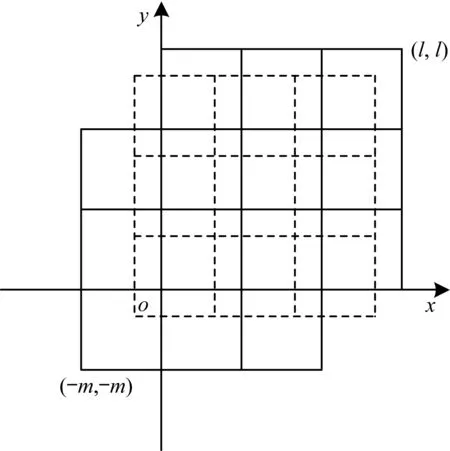
图5 移位策略示意图

下面对近似算法的近似比进行分析。每个单元格为m×m的正方形,这里假设单元格不包括上、右侧边界。假定Di为划分P(i,i)中所有单元格的最少数目充电器的并集。将划分P(i,i)中位于水平或垂直格线的所有单元格的集合成为P(i,i)的一个条块。用Hi和Vi分别表示D*中与P(i,i)的水平和垂直条块相交的所有单元格的集合。如果充电器与多个单元格相交,则它必须属于Hi或者Vi,且每个充电器最多与4个单元格相交,因此,有:

|Di|≤|D*|+|Hi|+2|Vi|

(2)

当a≠b时,一个充电器不可能既属于Va又属于Vb,即所有的集合Va,a=0,1,…,m-1都是两两不相交的。因此,有:

(3)

同理可得:

(4)

2.2 聚类分区算法

初始化移动位置集合M=Ø,聚类分区算法的具体步骤如下:

步骤1令k=1,S=Ø。

步骤2使用k-中心点算法进行分类并计算出每一类中点的最小包围圆[17]。

步骤3判断是否存在半径ri≤d0,i∈{1,2,…,k}的最小包围圆。若存在,则将这些聚类储存到集合S中,并且M=M∪S,然后从节点集N中去除类中的点,即N=N-S,判断集合S是否为空集,不满足转到步骤1,满足转到步骤4;若不存在,k=k+1,转到步骤3。

步骤4输出集合M。

已知k-中心点算法时间复杂度为O(k(n-k)2),而最小包围圆算法时间复杂度是线性的。假设第1次出现半径ri≤d0,i∈{1,2,…,k}的最小包围圆时k-中心点算法运行了k1次,此时最小包围圆内的节点数为n1,则运行总时间为:

O((n- 1)2+2·(n-2)2+…+k1·(n-k1)2)=

(5)

假设第2次出现半径ri≤d0,i∈{1,2,…,k}的最小包围圆时k-中心点算法运行了k2次,此时最小包围圆内的节点数为n2,则运行总时间为:

O((n-n1-1)2+2·(n-n1-2)2+…+

(6)

3 仿真与分析

本节展示了2种算法的仿真结果。仿真器以MATLAB和LINGO实现,仿真设置如表1所示。假设传感器节点随机部署在20 m×20 m平面中,其中距离平面2.82 m处的一组网格点间隔为1.414 m,以部署无线充电器。无线充电器的有效充电距离为3 m,即传感器节点与充电器的距离在这个范围内可以有效地补充电量,否则传感器节点的充电效率为0。

表1 仿真设置

图6和图7分别展示了当平面上随机部署传感器节点的数量为100时,2种算法得到的无线充电器的数量。其中,通过近似算法计算得到的充电器的数目为36个,而通过聚类分区算法计算得到的充电器的数目为35个。由于近似算法在移位策略中,处于左边界和上边界的点在移位之后将不再参与分区,因此会使计算出的充电器的数目上有一定的偏差。

图6 近似算法仿真结果

图7 聚类分区算法仿真结果

图8给出了近似算法、聚类分区算法和APB-GCS算法在选择充电器数量方面的比较结果。可以看出,由近似算法和聚类分区算法求得的充电器的数目比APB-GCS算法少得多,而近似算法与聚类分区算法相差不大。

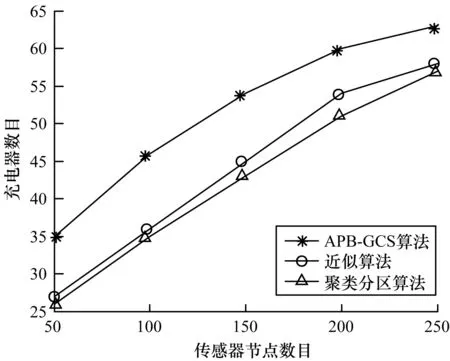
图8 本文算法与APB-GCS算法的充电器数目比较

4 结束语

本文定义无线可充电传感器网络中的充电覆盖问题,同时考虑传感器节点随机非均匀分布的特点,提出2种算法:将网络划分成网格的形式进行求解并利用移位策略减少充电器数目的近似算法,以及基于贪心算法思想的聚类分区算法。时间复杂度分析及仿真结果表明,聚类分区算法在减少充电器的数量方面性能更好,而且具有较低的时间复杂度。下一步将对充电器为传感器节点充电的时间以及WRSN中拓扑路由对充电的影响等问题进行研究。

[1] AKYILDIZ I F,SU W,SANKARASUBRAMANIAM Y,et al.Wireless sensor networks:a survey[J].Computer Networks,2002,38(4):393-422.

[2] RAULT T,BOUABDALLAH A,CHALLAL Y.Energy efficiency in wireless sensor networks:a top-down survey[J].Computer Networks,2014,67(8):104-122.

[3] RAJBA S,RAIF P,RAJBA T,et al.Wireless sensor networks in application to patients health monitoring[C]//Proceedings of IEEE Symposium on Computational Intelligence in Healthcare and E-health.Washington D.C.,USA:IEEE Computer Society,2013:94-98.

[4] KURS A,KARALIS A,MOFFATT R,et al.Wireless power transfer via strongly coupled magnetic resonances[J].Science,2007,317(5834):83-86.

[5] DAI H P,WU X B,XU L J,et al.Practical scheduling for stochastic event capture in wireless rechargeable sensor networks[C]//Proceedings of WCNC’13.Washington D.C.,USA:IEEE Computer Society,2013:986-991.

[6] DAI H P,XU L J,WU X B,et al.Impact of mobility on energy provisioning in wireless rechargeable sensor networks[C]//Proceedings of WCNC’13.Washington D.C.,USA:IEEE Computer Society,2013:962-967.

[7] 戴海鹏,陈贵海,徐力杰,等.一种高效有向无线充电器的布置算法[J].软件学报,2015,26(7):1711-1729.

[8] 胡 诚,汪 芸,王 辉.无线可充电传感器网络中充电规划研究进展[J].软件学报,2016,27(1):72-95.

[9] 刘 创,王 珺,吴 涵.无线可充电传感器网络的移动充电问题研究[J].计算机技术与发展,2016,26(3):162-167.

[10] LIAO J H,JIANG J R.Wireless charger deployment optimization for wireless rechargeable sensor networks[C]//Proceedings of International Conference on Ubi-Media Computing and Workshops.Washington D.C.,USA:IEEE Press,2014:160-164.

[11] LIAO J H,HONG C M,JIANG J R.An adaptive algorithm for charger deployment optimization in wireless rechargeable sensor networks[J].Frontiers in Artificial Intelligence and Applications,2015,274:2080-2089.

[12] HE S B,CHEN J M,JIANG F C,et al.Energy provisioning in wireless rechargeable sensor networks[C]//Proceedings of INFOCOM’11.Washington D.C.,USA:IEEE Computer Society,2011:2006-2014.

[13] LIN T L,LI S L,CHANG H Y.A power balance aware wireless charger deployment method for complete coverage in wireless rechargeable sensor networks[J].Energies,2016,9(9):695-708.

[14] PANG Y,LU Z,PAN M,et al.Charging coverage for energy replenishment in wireless sensor networks[J].IEEE International Conference on Networking,2014,43(3):251-254.

[15] 王继强.集合覆盖问题的模型与算法[J].计算机工程与应用,2013,49(17):15-17.

[16] DU D Z,KO K I,HU X.Design and analysis of approximation algorithms[M].Berlin,Germany:Springer,2011:123-136.

[17] WELZL E.Smallest enclosing disks(balls and ellipsoids)[M]//MAURER H.New Results and New Trends in Computer Science.Berlin,Germany:Springer,1991:359-370.