第五个优美不等式的一种简洁证法

安徽省芜湖市沈巷中学 (241012) 何业亮

安振平老师在文[1]提出二十六个优美不等式，其中第五个为：

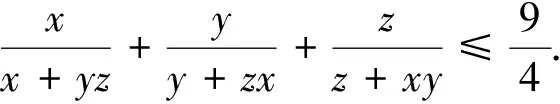
彭代元老师在文[2]中利用Schur不等式证明了该不等式，笔者认为此法有两大弊端：一是证明过程相当复杂，对思维能力和运算能力要求极高；二是条件x+y+z=1的使用，不仅给人一种“太突然”的感觉，也让人无法从中提炼出一般性的方法或技巧.本文给出第五个优美不等式问题的一种简洁证法，仅供大家参考.

证明：∵x，y，z为正实数，且x+y+z=1,

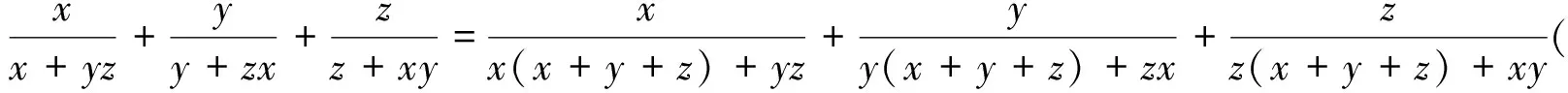
注意到安振平老师在文[3]中提出的恒等式：

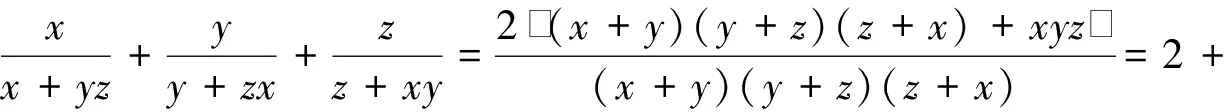
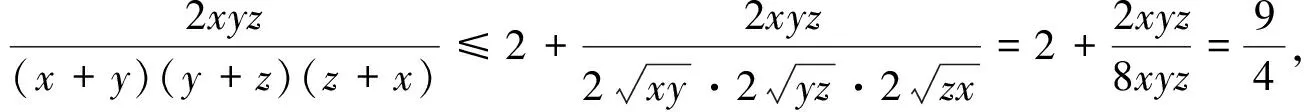
评述：利用条件1=x+y+z，在(甲)、(乙)两处实现齐次化，是此种证法的关键.笔者认为：齐次化是证明不等式的一种技巧，更是一种方法.下面给出几道题，供大家应验.

1.(第29届俄罗斯数学奥林匹克)设a，b，c∈

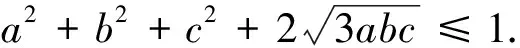
[1]安振平．二十六个优美不等式[J]．中学数学教学参考(上旬)，2010，1～2.

[2]彭代元．利用Schur不等式证明两个“优美不等式”[J]．数学教学通讯，2011(7).

[3]安振平．三个无理不等式之间的链接[J]．中学数学月刊，2011(7).