辽宁抚顺西露天矿南帮滑坡应力变化规律及影响因素分析

滕 超,王 雷,刘宝华，崔 原，贺 鑫，唐 浩

(辽宁省第十地质大队,辽宁 抚顺 113004)

0 引言

抚顺市西露天矿是一个连续开采一百多年的露天矿。长期高强度的矿山开采诱发一系列的地质环境问题,滑坡、崩塌、地裂缝等地质灾害频繁发生。2010年汛期，抚顺西露天矿南帮出现明显的地表裂缝。地表裂缝逐渐延展、贯通，形成典型的滑坡后缘圈椅状拉裂带。目前，滑坡形态平面上呈倒扇形，滑坡边界清晰，后缘以玄武岩和片麻岩不整合接触界线为界，前缘位于高程约-270～-310 m的西露天矿坑底，东侧边界受北西向F5断层控制，西侧边界呈北东向收敛。前缘和后缘高差在411.9～541.9 m，东西轴长约3 100 m，南北宽约1 500 m，滑坡体面积3.37 km2，整个滑体体积约4.52×108m3，为顺层岩质高陡边坡。滑坡后缘形成东西向贯通的高20～53 m的高陡滑坡壁、宽38～96 m的断陷洼地，垂直方向变形以沉降为主；滑坡前缘地表变形以滑坡鼓丘和鼓胀裂缝为主，垂直方向变形表现为鼓胀。伴随着矿山持续开采，滑坡的持续变形发展，局部出现解体破坏迹象，呈现出局部分层分级、分区分块破坏趋势，整体呈现顺向溃屈失稳的趋势。

对于顺层岩质边坡，受人类工程活动、地质环境条件等影响，坡体会出现上部岩层沿层面滑动，而坡底由于受阻而出现鼓出现象称为滑坡弯曲型变形即溃屈[1]。在坡脚处人工开挖形成的结构面坡度大于坡体岩层的倾角时，岩层的层面会出露于坡面上，尤其当坡体有软弱结构面存在并是连续面时，边坡容易发生顺层滑动。坡体变形发生和发育的过程，实际上是坡体内部岩土应力变化和发展的过程。通过坡体中的应力监测，监测坡体内部岩土的应力变化和分布状态，定量解析坡体变形破坏机制，认识坡体变形性质和规模，准确把握其稳定程度和发展趋势[2]。

1 应力监测系统

1.1 应力监测系统简介

本次应力监测系统主要采用土压力计和钻孔相结合的方式进行应力监测。在钻孔中，在不同深度分层埋设传感器，并且采用双向传感器联合应用的方法来测定滑坡前缘的应力状态(图1)。由于，土压力计一般埋设在土体中进行测量，本次采用在钻孔填充石英砂的方法进行测量。坡体前缘应力状态的改变通过力的传导传递给钻孔中的石英砂，传感器通过测定石英砂的应力，间接反映出坡体的应力变化情况。

本次应力监测系统中主要由TGCY-2-100A型土压力计、TGCD-2-200多通道工程测试仪、太阳能供电系统、无线传输系统以及采集控制分析软件组成。可实现无线远程自动化采集和传输，每3 小时数据自动更新。自动化采集方式可有效避免人工测试出现的误差和大量繁琐的工作。

1.2 TGCY-2-100A型土压力计的工作原理

TGCY-2-100A型土压力计采用振弦式传感器，是以拉紧的金属弦作为敏感元件的谐振式传感器。振弦一端固定，另一端连接在弹性感压膜片上。弦的中部固定有一块软铁，置于磁铁和线圈构成激励器的磁场中。在电激励下，振弦按其固有频率振动。改变振弦的张力F，可以得到不同的振动频率f，张力与谐振频率成单值函数关系。

谐振频率与振弦张力之间关系：

(1)

式中：f——谐振频率/Hz；

F——振弦张力/N；

m——振弦质量/kg；

l——振弦长度/cm。

当振荡器给出激发脉冲，继电器吸合，电流通过磁铁线圈，使磁铁吸住振弦。脉冲停止后松开振弦，振弦自由振动，在线圈中产生的感应电动势经继电器常闭接点输出。感应电动势的频率即为振弦的谐振频率，通过测量感应电动势的频率即可测量振弦张力的大小。振弦张力与传感器上部压力线性相关，即通过测量振弦的谐振频率获得传感器上部压力。

1.3 应力监测点的布设

监测数据显示，西露天矿南帮滑坡在坡体中下部的F2断层部位垂直变形速率发生明显的变化，在F2断层以南坡体垂直变形以沉降为主，在F2断层以北坡体垂直变形以抬升为主。

为掌握滑坡前缘的应力分布和变化情况，及时、准确地对西露天矿南帮滑坡变形发展趋势进行分析和预测。在滑坡体的下部，F2断层以北(上盘)，自西向东沿着矿区坐标的四条测线上共布设4个应力监测点(图2)。每个应力监测孔内由上至下每20 m按东西、南、北方向各布设一个传感器，共布设8 个传感器。

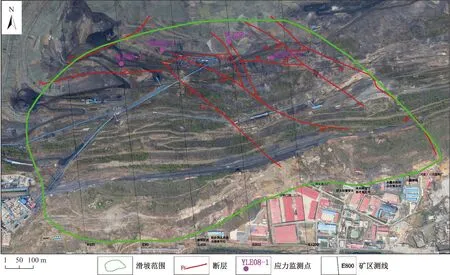
图2 应力监测系统监测点分布图Fig.2 Distribution map showing the monitoring points of the stress monitoring system

2 应力监测成果综合分析

2.1 应力监测结果分析

通过对4 个应力监测点、32 个土压力计传感器的监测成果和应力监测点钻孔地质资料的综合分析，得出结论如下：

(1)随着传感器埋置深度的增大，上覆土体自重应力增大，围压亦随之增大，应力测量值亦随深度线性增长，变化趋势一致(图3、图4)。峰值应力所对应的应变值随之增大，岩石的变形特征明显地表现出低围压下的脆性特性向高围压下的塑性特性转变的规律。

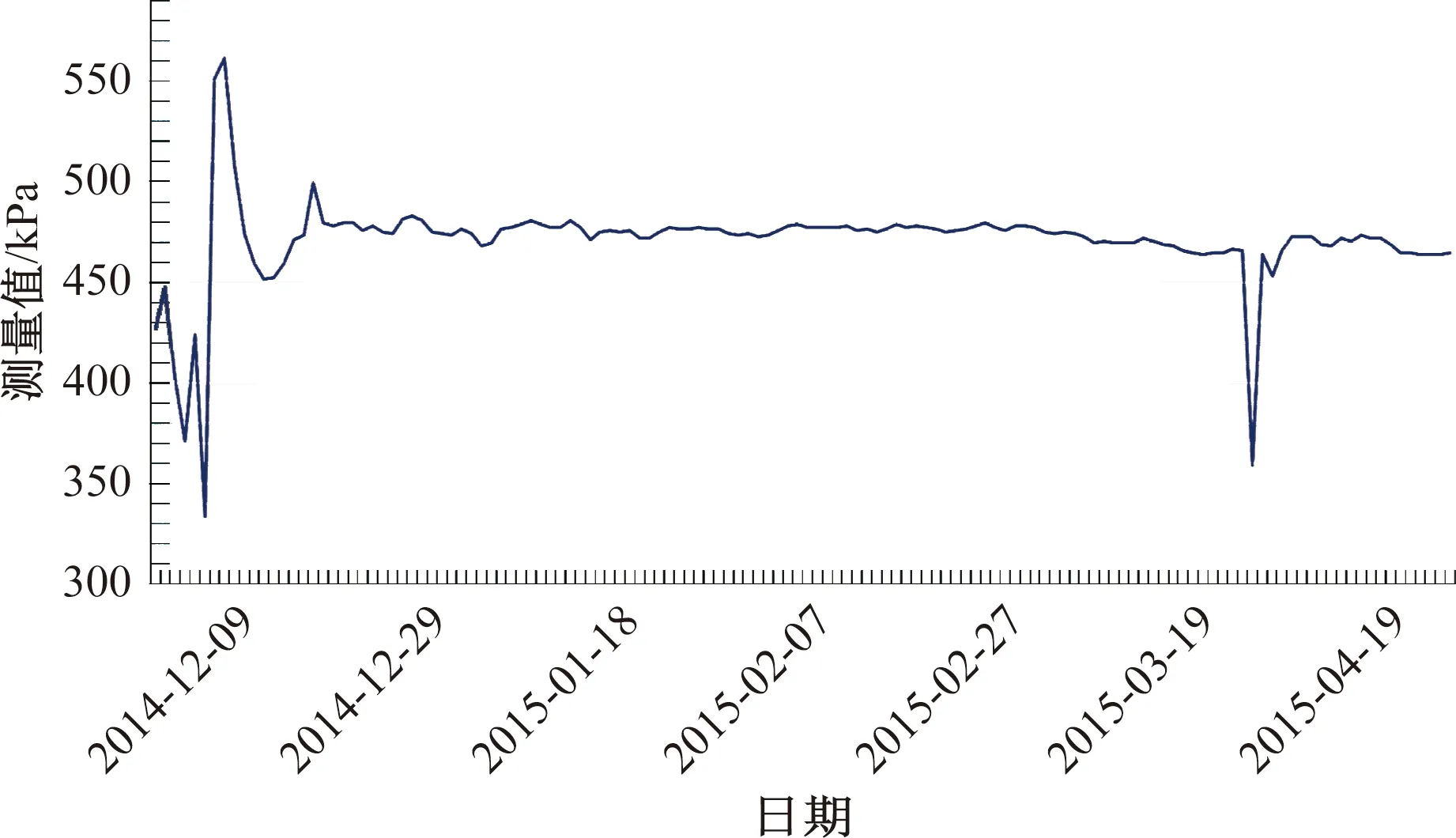
图3 YLEW0-2应力监测点1号传感器应力测量值Fig.3 The measured stress values from the No.1 transducer at YLEW0-2 stress monitoring point

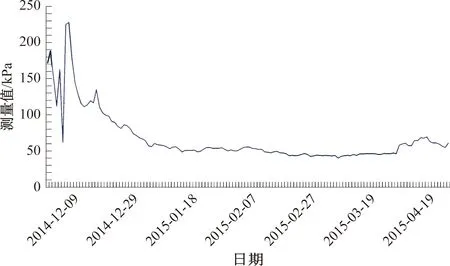
图4 YLEW0-2应力监测点3号传感器应力测量值Fig.4 The measured stress values from the No.3transducer at YLEW0-2 stress monitoring point

图3和图4是位于EW0测线-174.8 m标高处，埋深分别为80 m、60 m的南北向受力的1 号、3 号传感器的监测数据。可以看到初始时应力测量值波动较大，出现明显的震荡，推测是由于传感器在埋设过程中受扰动影响大，所以在接收数据前期出现一定程度的波动，稳定后测得的应力曲线较为平缓。80 m处应力明显大于20 m处应力，总体上从浅到深呈应力增加的趋势。

同时，由于滑坡是南北向滑动，应力测量值显示出南北向受力总体大于东西向，但是，局部由于受坑内错综复杂的断层影响，数据会出现非规律性变形趋势。

(2)岩体是在地质历史过程中形成的、已经遭受过变形破坏、具有一定成分和结构并赋存于一定地质环境中的地质体。坡体的岩体在形成过程中，受各种因素影响，形成一定的节理裂隙、断裂构造等。受滑坡变形作用的影响，坡体原有的岩体结构将会改变，一些节理裂隙发育贯穿连通，改变了岩体内部原有的应力状态。岩体中的结构面具有优势方位及岩体赋存环境的差异使得岩体具有各项异性，岩体的物理力学性质随取向性不同而具有明显方向性差异。

YLE10-1监测孔的传感器3、传感器4为同一埋深不同方向放置的两个传感器。传感器3、传感器4数据数值，变化趋势具有一致性，未能体现各向异性，反应该层位岩体完整性程度较好，节理裂隙不发育，未被滑面切割(图5)。

图5 YLE10-1监测孔的3、4号传感器测量值Fig.5 The measured values from the No.3 and No.4 transducers at YLE10-1 stress monitoring point

2.2 影响因素的分析

岩体的空间应力状态极其复杂，既取决于地区的地质、地貌发展史，同时又受岩性、局部构造、地形地貌影响。对于西露天矿南帮滑坡，其空间应力状态主要受采矿活动和降水两方面因素影响[6-8]。此外，受抚顺地区特殊地质环境条件和采矿活动的影响，还受矿震的影响。结合对地面巡查和其他变形监测数据的成果分析，得出采矿活动、降水、矿震也是影响西露天矿南帮滑坡变形发展的主导因素。

2.2.1采矿活动的影响

由于开挖卸荷，引起边坡岩体应力状态的改变，同时，岩体内的部分节理、裂隙出露地表，不仅受到物理化学风化等浅表地质作用的改造，而且容易受到人类工程活动的影响。这些都将引起边坡岩体的结构及物理力学性质发生变化，进而导致滑坡的变形破坏。这一过程是渐进的，与滑坡体不同区段所处空间位置不同、地质环境条件不同有关。不同区段空间应力状态不同。

图6 YLE10-1应力监测点3号传感器监测值突变示意图Fig.6 Graph showing the measured values of the No.3 transducer at YLE10-1 stress monitoring point

YLE10-1应力监测点位于E1000测线-203 m标高处，在该处下方-300 m标高处为同期西露天矿露天开采主工作区。在2016年4月10日之前，该监测孔内埋深在56.5 m泥化夹层部位的南北向受力的3 号传感器，应力测量值一直处于应力积累阶段，应力值不断持续小幅上升；4月10日，应力由积累阶段进入到突变阶段，坡体原有的应力平衡状态被破坏，坡体应力结构随之改变，应力测量值由60 kPa突变为-1 000 多kPa，后增大到20 000 kPa，最终传感器被剪断(图6)。此后，4月20日，埋深在76.5 m玄武岩部位南北向受力的1 号传感器出现类似现象被剪断。4月23日，2 号、4 号传感器也出现类似现象。

由图7可见，随着坑内开采深度的加大，坡体原有的应力平衡状态遭到破坏，坡体将会产生位移和形变，软弱岩层部位表现最为明显。随着变形的持续发展，其他岩层部位也会出现类似的坡体结构破坏迹象。边坡变形破坏前处于应力积累阶段，变形破坏时使集中的应力得到释放从而应力值迅速下降。边坡岩体在变形破坏过程中，岩体的内部结构和外形不断变化，应力状态随之不断调整，直至达到新的应力平衡状态。

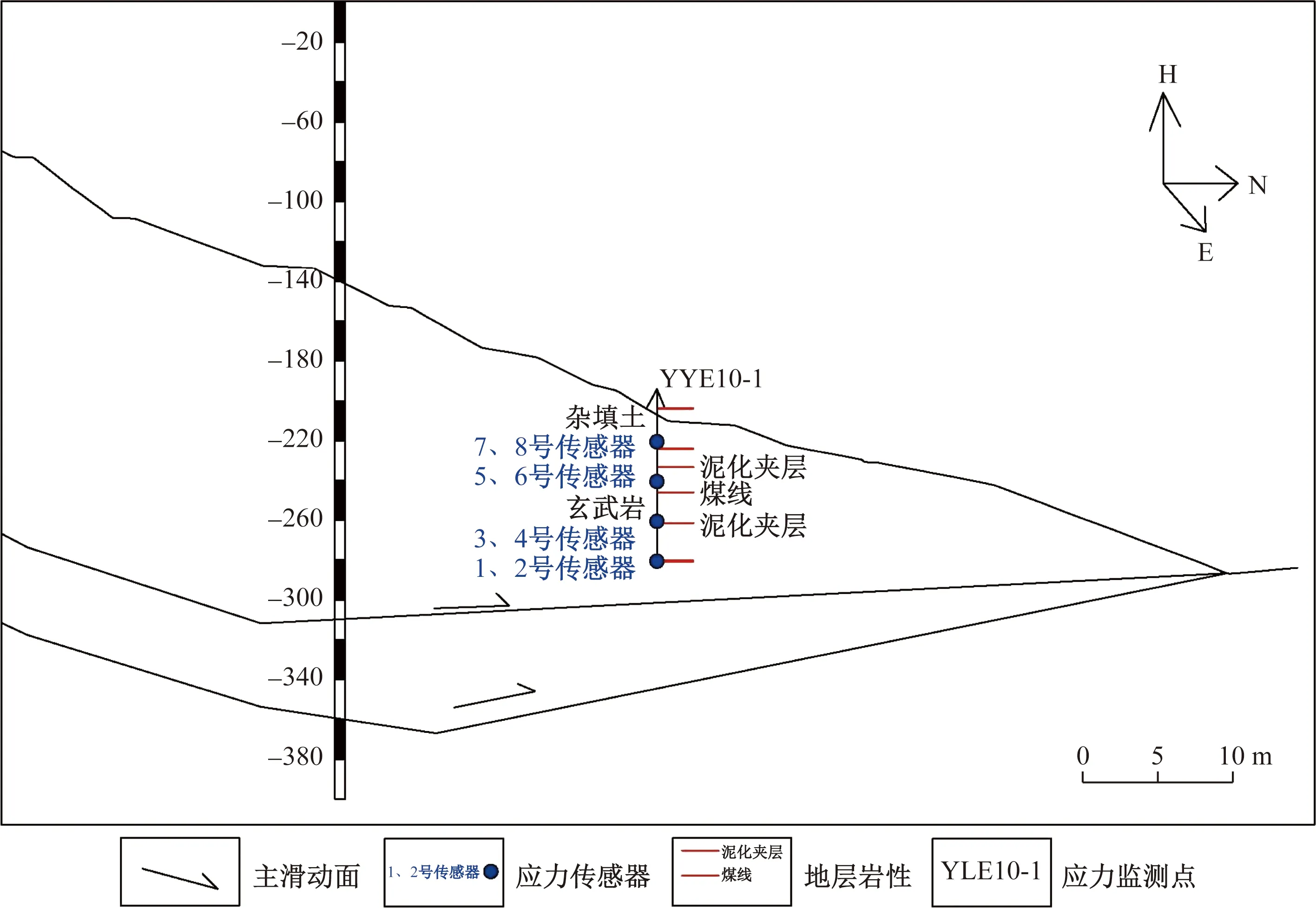
图7 YLE10-1应力监测点剖面图Fig.7 Profile map of the YLE10-1 stress monitoring point

2.2.2降水的影响

在没有降雨、降雪等外界补给水时，坡体内维持原有的地下水平衡，与此同时，坡体内应力场也维持原来分布，保持坡体的平衡。而当有外界水补给坡体时，坡体内含水量、水头等将发生改变，渗流也发生变化，应力场也发生相应改变以适应新的渗流场，达到坡体自身稳定的调整[9]。大气降水改变了坡体自重，增大了边坡的下滑力，同时降低了滑坡体的抗剪强度。因而，如图8所示，通过对EW0测线-174 m标高处的YLEWO-2应力监测点埋深80 m的1号传感器监测数据与降雨量的统计分析，得出在季节性集中降水时期应力值有明显增大现象，当边坡自身调整以适应新的渗流场、应力场以达到平衡时，应力值出现衰弱，恢复稳定。

图8 应力监测数据与大气降水的相关性曲线图Fig.8 The correlation curve graph between the monitoring stress values and the precipitation

2.2.3矿震的影响

矿震对应力监测值的影响:西露天矿边坡，工矿活动剧烈(上部为露天开采，深部为井工采)，伴随着煤炭资源的开采，采煤诱发的地质灾害频频发生，尤其是矿震。矿震给边坡岩体以突然的初始位移，使岩体受冲击而产生反常应力，岩体以本身的震动特征来决定这种应力波的传播方式。由于岩体存在有阻尼，因此激发产生的震动最终会消失。如图9所示，通过对EW0测线-174 m标高处的YLEWO-2应力监测点埋深80 m的1号传感器应力测量值与矿震数据的统计分析，得出矿震影响了应力值的变化，在发生矿震后应力值出现小幅度的下降趋势，随后逐渐恢复。矿震对斜坡稳定性的影响表现为累计和触发等两方面效应。一方面震动可通过松动斜坡岩体结构，造成破裂面和引起软弱面错位等多种方式，留下降低斜坡稳定性的痕迹。反复作用造成的后果积累，则可能最终导致斜坡失稳；另一方面，矿震产生应力波可在裂隙或软弱夹层中产生反射应力波，造成瞬时拉应力。因而当岩体中某些软弱结构面本身已具有或储有足够的剪切应变能时，应力波促使这些结构面发生破裂。同时，边坡岩体在矿震动应力作用下可因骨架的迅速变形造成空隙水压力的突然变化，从而导致岩体失稳。

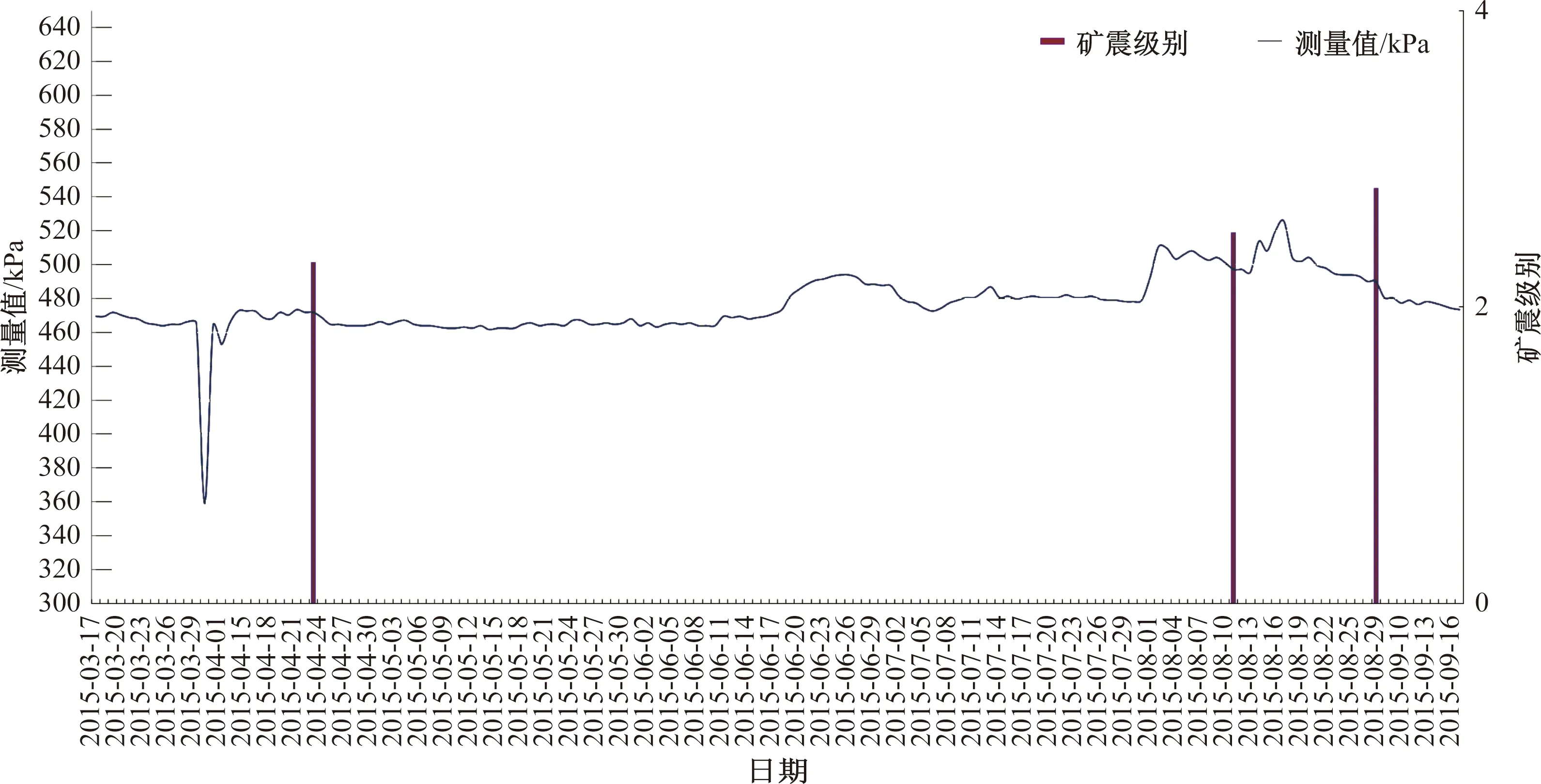
图9 应力监测数据与矿震的相关性曲线图Fig.9 The correlation curve graph between the monitoring stress values and the mine earthquake

3 数值模拟

3.1 有限元强度折减法的原理和屈服准则

建立在强度折减有限元分析基础上的边坡稳定性分析的基本原理是：将边坡强度参数粘聚力C和内摩擦角σ同时除以一个折减系数F,得到一组新的粘聚力C′和内摩擦角σ′,即：

(2)

(3)

式中：C——粘聚力/N；

σ——内摩擦角/(°)；

F——折减系数；

C′——折减后的粘聚力/N；

σ′——折减后的内摩擦角/(°)。

折减后的粘聚力C′和内摩擦角σ′作为一组新的强度参数再输入到ANSYS中进行计算，直至不收敛时计算的折减系数就是边坡的安全系。此时，边坡达到极限状态，发生剪切破坏数[10]，同时可得到临界滑动面所在的塑性区。

有限元强度折减法中岩土材料本构模型采用理想弹塑性模型。ANSYS有限元分析软件采用广义米赛斯准则(公式4)。

(4)

式中：I1代表应力张量的第一不变量；

J2代表应力偏张量的第二不变量；

∂、k代表与岩土材料内摩擦角σ和粘聚力C有关的常数[11]，取不同的数得到不同的屈服面，得到不同的安全系数。

3.2 地质建模

选取地面变形较强烈的E1200剖面进行数值模拟，把E1200剖面计算模型简化为平面应变问题。假定边坡所承受的外力不随Z轴变化，只考虑重力的作用，位移和应变都发生在自身平面内。基于真实地层情况，采用与地层分布一致的多层弹塑性理论模型，模型采用4 节点平面单元。模型的边界约束条件为：后方为y方向固定约束；底部为x、y方向固定约束；前部和顶部为自由边界。E1200剖面模型共计667 个节点，208 个单元(图10)。

图10 E1200模型Fig.10 E1200 model

3.3 数值模拟

当折减系数为0.98时，迭代过程出现不收敛，此时X方向应力和第三主应力均发生塑性变形，从坡脚贯通到坡顶(图11、图12)，表明E1200测线的稳定系数为0.98。从应力角度分析，应力沿着地层在坡脚软弱岩层处集中释放。塑性变形都发生在软弱层位置，与应力监测结果相吻合。

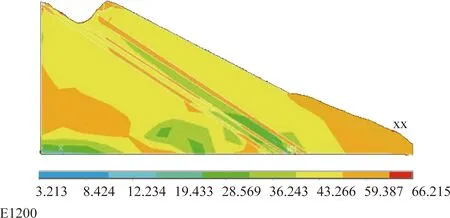
图11 E1200剖面X方向应力等值线Fig.11 stress contour in X direction of E400 profile

图12 E1200剖面第三主应力云图Fig.12 third principal stress contour of E1200 profile

4 结论

(1)本文通过在西露天矿南帮滑坡前缘埋设土压力计，监测坡体的应力变化情况，分析、预测坡体的变形发展趋势。对监测成果的分析，得出随着传感器埋置深度的增大，上覆土体自重应力增大，围压亦随之增大，应力测量值亦随深度线性增长。由于滑坡为向北滑移，南北向受力总体大于东西向受力。临近传感器变化趋势具有一致性，未能体现各向异性，反应该层位岩体完整性程度较好，节理裂隙不发育，未被滑面切割。

(2)通过对监测数据、地质环境条件、降雨量、人类工程活动等的综合分析，得出采矿活动、大气降水、矿震是影响坡体应力状态的主导因素，也是影响滑坡稳定性的主导因素。

(3)通过基于ANSYS的有限元强度折减法对地表变形较严重的E1200测线进行数值模拟，得出E1200测线的稳定系数为0.98。应力沿着地层在坡脚软弱岩层处集中释放。塑性变形发生在软弱层位置，与应力监测结果相吻合。

由于现有的应力监测点数量有限，不能形成监测网络，不能绘制应力场，不能很好地分析坡体的应力分布情况。

参考文献：

[1] 肖慧,侯克鹏,杜俊.对层状岩质状边坡不同层数溃屈失稳破坏的研究[J].科学技术与工程,2014,14(2):224-227.

XIAO Hui,HOU Kepeng,DU Jun.The study on buckling failure of different layer of layer rock mass slope[J].Science Technology and Engineering,2014,14(2):224-227.

[2] 戴志仁.岩质边坡应力场特征与参数敏感度分析[D].西安:长安大学,2007.

DAI Zhiren. Study on the characteristic of stress and the sensitivity of parameters in rockmass slope[D].Xi’an： Chang’an University，2007.

[3] PEATTIE K R, SPARROW R W. The fundamental action of earth pressure cells[J] Journal of the Mechanics and Physics of Solids, 1954,2(3):141-155.

[4] 张海丰,马保松,王福芝.被动土拱效应对土压力计匹配误差的影响[J].岩土工程学报,2016,38(2):350-354.

ZHANG Haifeng， MA Baosong，WANG Fuzhi.Influence of passive soil arching effect on matching error of earth pressure cells[J].Chinese Journal of Geotechnical Engineering,2016,38(2):350-354.

[5] TORY A, SPARROW R. The influence of diaphragm flexibility on the performance of an earth pressure cell [J] Journal of Scientific Instruments,1967, 44(9):781.

[6] 程宏,杨久林,温海民.某矿残采边坡应力场分布规律模拟研究[J].现代矿业,2011,7(7):4-6.

CHENG Hong，YANG Jiulin，WEN Haimin.Numerical simulation on the displacement field distribution of residual mining slope of a mine[J].Modern Mining,2011,7(7):4-6.

[7] 王建国.残采期抚顺西露天矿动力相应研究[D].阜新:辽宁工程技术大学,2006.

WANG Jianguo.Study on dynamic response of fushun West Open Pit Mine slope in remaining coal mining period[D].Fuxin： Liaoning Technical University，2006.

[8] 张电吉.裂隙岩质边坡渗流场与应力场耦合分析及工程应用[D].武汉:中国科学院武汉岩土力学研究所,2003.

ZHANG Dianji.Analysis and application of coupled seepage and stress fields in fractured rock slope [D]Wuhan: Institute of Rock and Soil Mechanics，The Chinese Academy of Sciences，2006.

[9] 谭超.地下水对滑坡的力学作用研究[D].成都:成都理工大学,2009.

TAN Chao. Study on groundwater to the mechanical function of landslide [D]Chengdu：Chengdu University of Technology，2009.

[10] 赵尚毅,郑颖人，时卫民，等.用有限元强度折减法求边坡稳定安全系数[J].岩土工程学报,2002,24(3):343-346.

ZHAO Shangyi，ZHENG Yingren，SHI Weimin，et al.Analysis on safety factor of slope by strength reduction FEM[J]. Chinese Journal of Geotechnical Engineering, 2002,24(3):343-346.

[11] 柳林超,梁波,刁吉.基于ANSYS的有限元强度折减法求边坡安全系数[J].重庆建筑大学学报,2009,5(2):28-35.

LIU Linchao，LIANG Bo，DIAO Ji.Using FEM strength reduction method based on ANSYS to solve slope safety coefficients[J].Journal of Chong Qing Jiao Tong University (Natural Science)， 2009,5(2):28-35.