无资料地区水文模型参数估算方法比较研究

徐长江，杨无双，汪青静，陈 华

(1.长江水利委员会水文局，武汉 430010；2.武汉大学水资源与水电工程科学国家重点实验室，武汉 430072)

0 引 言

随着科学技术的进步和人们对于防洪安全意识的提高，人们对水文预报的准确性以及时空尺度的要求越来越高，这促使了无资料地区水文模拟的研究越来越受重视。2003年针对发展中国家的无水文观测资料或者资料不全的全球重点研究计划(PUB计划)开展以来，关于无资料地区的水文模拟研究无论在理论还是应用上都取得了很多成果[1-3]。但由于流域的多样性、水文机理的复杂性、模型的局限性和资料的限制等原因，还有很多难题未解决，所以在未来相当长的一段时间内，无资料流域的水文模拟仍然是水文研究的重难点之一[4]。

Parajka[5]等人总结了PUB计划实施十年间(2003-2013年)的部分研究成果，发现大多数研究区域都集中在北美洲、欧洲和澳大利亚。作为世界上人口最多的发展中国家，我国人均水资源十分有限，所以水资源规划和管理需要更准确的水文预报，另外，地域辽阔、气候条件多变的特性也使得在许多无资料流域以及PUB科学问题方面的研究需要探索水文预报新的理论与方法[4, 6]，因此在中国开展无资料地区水文预报的研究是十分必要的。本文在PUB计划研究成果的基础上，将4种无资料地区水文模型参数估算方法应用到湘江流域，验证各方法的可行性，为其在中国无资料地区的应用提供依据与参考。

1 研究区域与数据

1.1 研究区域

湘江流域为长江流域洞庭湖水系，地处北纬24°31′～29°00′，东经110°30′～114°00′之间，位于亚热带季风气候区，降水充足，但年内分布不均，主要集中在3-7月间。流域水系发达，河网密布，干流总长度约为856 km，流域面积为9.48 万km2。本文根据实测水文资料以及流域地形特征，利用湘江流域DEM图(数字高程模型)划分子流域，从中选取了11个子流域为研究区域。

1.2 数据与处理

1.2.1 气象数据

本文研究所用气象数据是洞庭湖区水文年鉴中摘录的2006-2014年共9年的日降水、日蒸发和日径流实测数据。其中，流域内雨量站有274个站点，蒸发站有14个站点，考虑到有些雨量站和蒸发站分布在流域边界上或流域外且分布不均匀，因此利用泰森多边形法对各子流域的面雨量、面蒸发量进行了整理计算[7]，结果如表1所示。

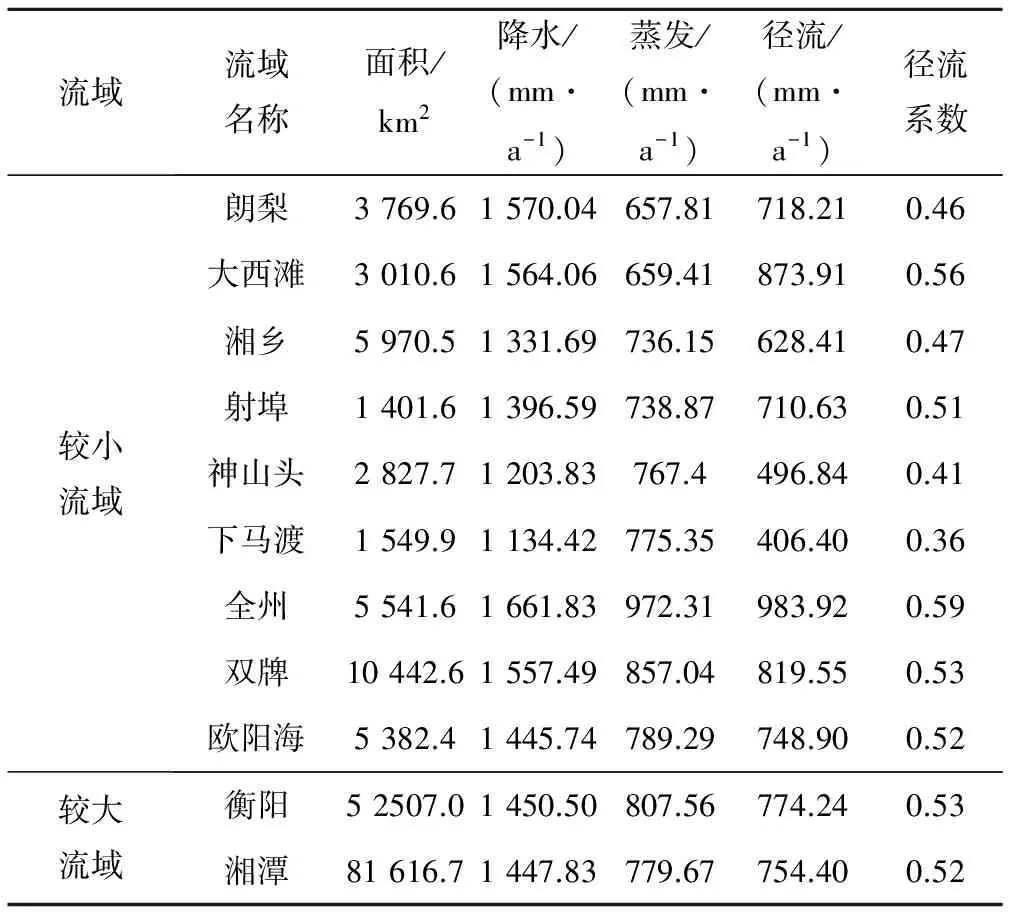
表1 流域气象特征值Tab.1 Meteorological Characteristics in Xiangjiang River Basin

1.2.2 流域下垫面特征值

流域下垫面特征值是指一个流域的坡度、植被、土壤、地形地貌、流域形状等物理性质，决定着流域的蓄水量、透水性等特性的不同，因而对流域产汇流存在着很大的影响。本文根据现有资料共选取了8种下垫面特征值，如表2所示。

2 模型与方法

2.1 新安江模型

新安江模型是在1973年由河海大学赵人俊教授领导的研究组设计的国内第一个完整的流域水文模型。该模型在国内外湿润半湿润地区的模拟效果普遍较好，应用十分广泛[9-11]。本文研究使用三水源新安江模型，共15个参数，每个参数都具有明确的物理意义[12,13]。

表2 流域下垫面特征值 Tab.2 Underlying surface characteristics in Xiangjiang River Basin

2.1.1 SCE-UA优化算法

SCE-UA(Shuffled Complex Evolution)算法是一种非常有效的解决概念性水文模型参数率定问题的全局优化算法[14-16]。该算法主要基于信息共享和自然生物进化的理念[17]，整合了全局抽样以及复合形进化等概念的优势[18]，这些特性能够确保充分利用样本信息，大大提高了算法的收敛效率[16, 19]，因此被广泛地应用于概念性水文模型参数的率定问题[20-22]。SCE-UA优化算法的参数比较多，但多数可以根据已有研究结果确定，仅有复合型个数p需要根据实际问题确定[17]。p值越大，收敛于全局平均的概率越大，但计算量也越大，反之亦然[23]。本文取经验值p=2。

2.1.2 目标函数

本文采用纳西效率系数(NSE)和水量相对误差(RE)作为模型模拟精度的评价指标。

(1)

(2)

式中：Qsim,i为模拟流量序列；Qobs,i为实测流量序列。

2.2 Sobol’敏感性分析方法

由于模型参数较多，一些不敏感参数对水文模拟的结果影响较小，本文区分出较敏感参数和不敏感参数，只对敏感参数用各移植方法进行移植，可以减少参数间的非独立性，从而降低模型的不确定性。Sobol’是一种非常有效的基于方差原理的全局敏感性定量分析方法[24]。该方法不仅能定量描述单个独立参数的敏感性，而且考虑到不同参数间相互作用对模型输出产生影响，能有效地分析非线性模型中参数之间相互作用的敏感性[25]，较局部敏感性分析更接近实际，因此近年来受到了广泛的应用[25-27]。

Sobol’方法首先将参数抽样样本转化到一个多维单元体中，将模型目标函数分解为单个模型参数与参数间相互作用的子函数之和，根据方差分解原理，模型总方差也可以分解为单个模型参数与参数间相互作用的方差之和，通过蒙特卡洛拟合求解方法对目标函数的总方差以及各子项的偏方差进行估算，最后根据各子项偏方差对总方差的贡献比例来表示模型参数及其相互作用的敏感程度[28]。

抽样方法上，本研究采用的是拉丁超立方抽样方法，与传统的蒙特卡洛抽样方法相比，该方法能够使产生的随机点更均匀地分布在采样区域内，能够有效地用采样点反映随机变量的整体分布[29, 30]。

2.3 参数移植方法

目前对无资料地区径流预报常用的方法为区域化方法。该方法是在一定范围内，将有资料流域的水文信息比如水文模型参数通过一定的方法移植到无资料流域，从而实现对无资料流域的预报，由于区域化方法能够利用流域下垫面特征值等信息，所以能够有效地降低不确定性影响，从而提高预报精度。常用的区域化方法有多元回归法、空间邻近法、流域物理特性相似法以及全局平均法[31]。

(1)多元回归法：在有资料流域，以新安江模型参数为因变量，以流域下垫面物理特征值为自变量建立多元回归方程，根据多元回归方程和无资料地区的下垫面特征值反推出模型参数值，进而达到参数移植的目的。本文通过逐步回归法建立敏感参数与流域下垫面特征值之间的关系。

(2)空间邻近法：直接以地理上相近的有资料流域的模型参数作为本流域的模型参数。本文中两个流域间的距离利用流域质心间的经纬度进行计算。

(3)流域物理特性相似法：通过比较各流域的相似性，以与无资料流域最相似流域的模型参数作为无资料流域的模型参数。本文采用下式计算流域相似度，Z的范围为0～1，越小表示两个流域越相似[32]：

(3)

式中：XG和XU分别为有资料流域和无资料流域的下垫面特征值；ΔX为某属性在各流域中最大值和最小值的差值；k为下垫面特征值个数。

(4)全局平均法：将研究区域内，各有资料流域模型参数的平均值移植到无资料流域进而进行水文模拟，本文中该方法仅针对两个较大流域使用。本文对选取的11个子流域，依次假定其中一个流域为“无资料”流域，其余为有资料流域，通过以上区域化方法将有资料流域的模型敏感参数移植到“无资料”流域，其余不敏感参数则用各有资料流域模型参数的平均值代替，检验各方法的可行性及其优劣。

3 结果与讨论

3.1 参数敏感性分析结果

不同目标函数侧重不同的径流特性，因此不同目标函数下的参数敏感性也会有所差异[27]，本文以纳西效率系数(NSE)和水量相对误差(RE)作为目标函数对新安江模型参数敏感性进行分析(图1)。

图1 不同流域各参数的一阶敏感度和总敏感度Fig.1 The first-order sensitivity and total sensitivity of each parameter in different watersheds

图1以大西滩和湘潭流域为例画出了不同目标函数下各参数的一阶敏感度和总敏感度，文中指定当一阶敏感度超过阈值(10%)时，该参数为敏感参数[27]。结果显示，当目标函数为NSE时，主要的敏感参数有KG、CG、N、NK，其中CG控制着地下水的径流过程，对洪水过程线影响较大，因此较为敏感；而KG控制着地下水占比；N和NK决定着地面汇流单位线的形状和大小，对洪峰流量的模拟都有很大影响，因此较敏感。当目标函数为RE时，主要的敏感参数有CG和KE，其中KE控制着水量平衡，是影响产流量最为重要的参数，对水量计算非常重要，因此具有较强的敏感性；而CG控制着地下退水过程的快慢，对最终的流量过程有很大影响，因此也较敏感。表3汇总了各流域敏感性参数。

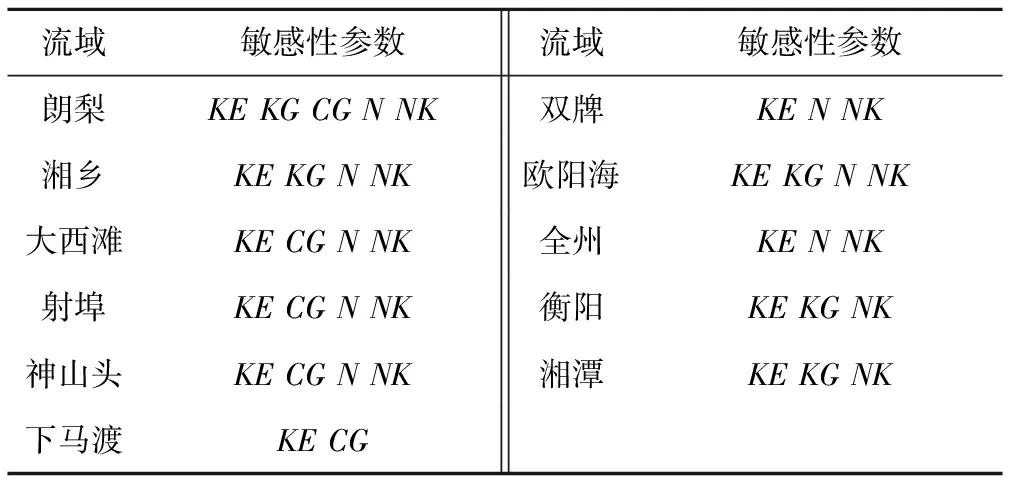
表3 各流域敏感性参数Tab.3 Sensitivity parameters of each Sub-basin

3.2 参数移植结果

3.2.1 模型率定

建立基于SCE-UA全局优化算法的三水源新安江模型，参数率定结果见表4。从表4中可以看出， 11个子流域的纳西效率系数均能达到0.75以上，说明模拟结果较好。另以大西滩站和衡阳站为例画出了2013年两个站的日流量过程示意图，图示结果也表明新安江模型能够较好地模拟大西滩站和衡阳站的流量过程，如图2和图3所示。以上结果表明新安江模型能够较准确地模拟湘江流域的降雨径流关系，可用于无资料流域水文模型参数估算方法的研究。

表4 各子流域模拟结果Tab.4 Simulation results of each sub-basin

图2 大西滩站新安江模型2013年日流量过程线Fig.2 The 2013 daily flow hydrograph by Xin'anjiang Model at Daxitan Station

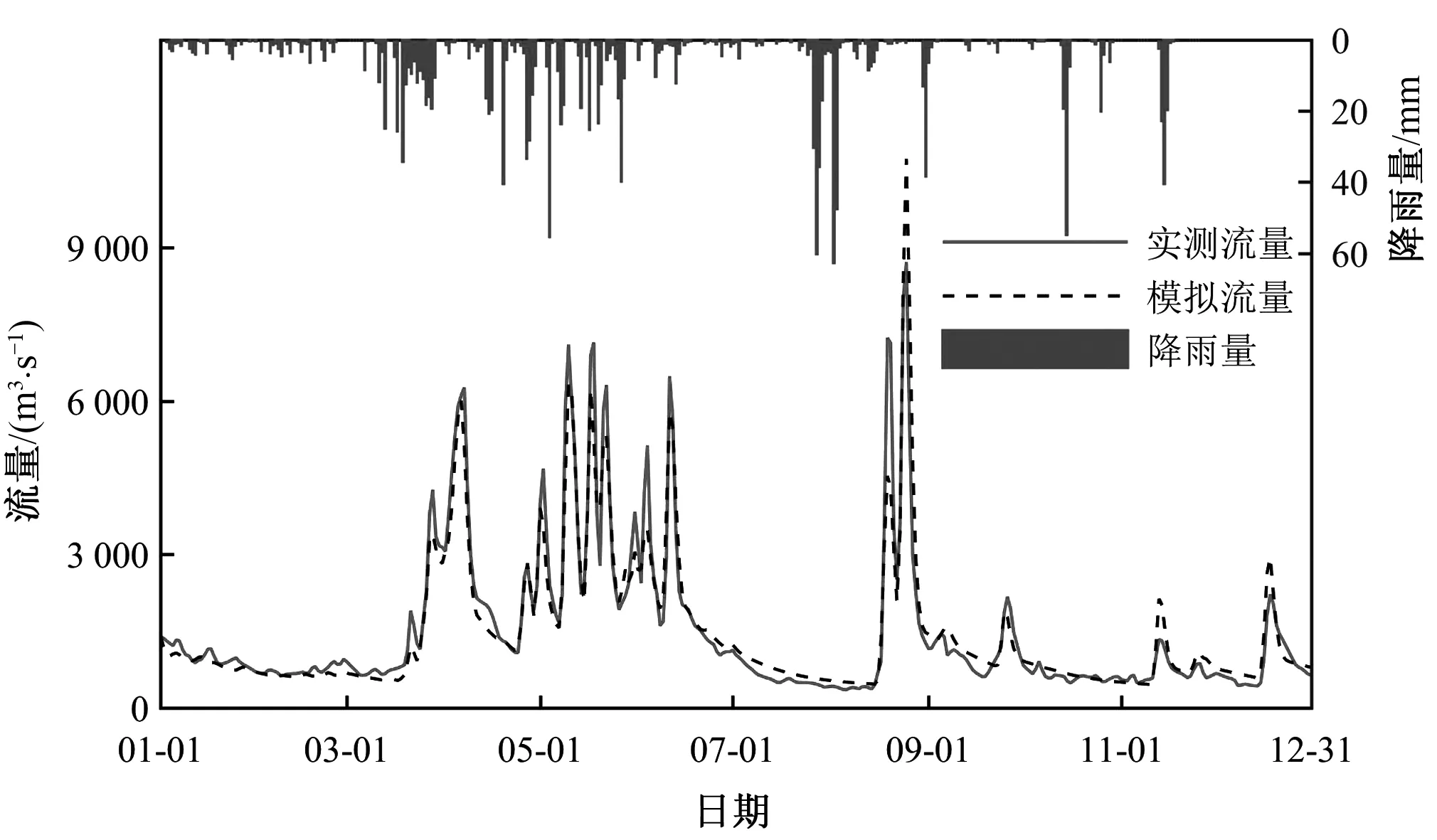
图3 衡阳站新安江模型2013年日流量过程线Fig.3 The 2013 daily flow hydrograph by Xin'anjiang Model at Hengyang Station

3.2.2 区域化方法移植结果

将建立的区域化方法应用到无资料流域，结果如表5以及图4所示。可以看出，通过参数移植，各“无资料”流域的纳西效率系数均在0.65以上，说明各区域化方法在湘江流域是适用的，且能得到较好的结果。另外对比各流域之间的结果可以看出，各区域化方法在不同无资料地区的表现存在差异，如在朗梨、射埠和下马渡3个子流域内，多元回归法应用结果最好；而在全州流域，结果正好相反；另外在湘乡、神山头、欧阳海、衡阳和湘潭5个子流域内，多元回归法和物理特性相似法的结果相似，且优于空间邻近法和全局平均法；而在大西滩流域，3种区域化方法的结果大致相同，且和实测资料模拟结果很接近。

表5 参数移植结果Tab.5 The Results of Parameter Transplant

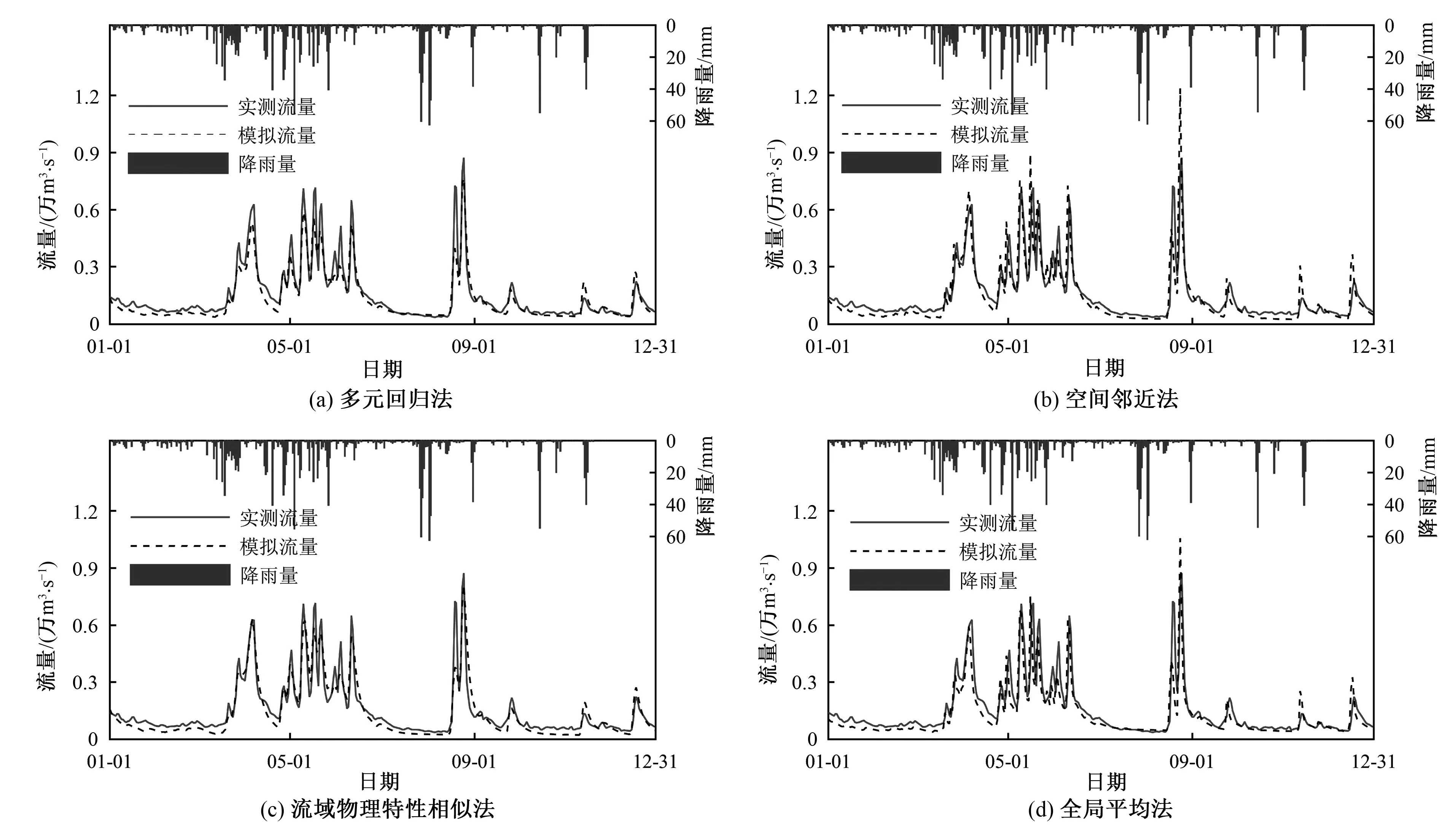
图4 衡阳站参数移植2013年日流量过程线Fig.4 The 2013 daily flow hydrograph by parameter transplant at hengyang station

4 结 语

本文在总结PUB计划研究成果的基础上，研究了空间邻近法、物理特性相似法、多元回归法和全局平均法4种无资料地区参数移植方法在湘江流域的可行性。结果表明，各区域化方法在湘江流域上是适用的，能够较好地模拟出湘江流域内不同子流域的降雨径流关系，但在不同的流域上表现各异，优劣不同。但就总体来看，多元回归法的移植效果普遍较好，空间邻近法和流域物理特性相似法次之，全局平均法较差。此外，虽然区域化方法结果较实测资料模拟结果的精度相对偏低，但对无资料地区，通过这些方法进行水文预报仍不失为一种有效的解决方法，并可为其在中国无资料地区的研究和应用提供参考。

□

参考文献：

[1] Bao Z, Zhang J, Liu J, et al. Comparison of regionalization approaches based on regression and similarity for predictions in ungauged catchments under multiple hydro-climatic conditions [J]. Journal of Hydrology, 2012, 466:37-46.

[2] Samuel J, Coulibaly P, Metcalfe R A. Estimation of Continuous Streamflow in Ontario Ungauged Basins: Comparison of Regionalization Methods [J]. Journal of Hydrologic Engineering, 2011,16(5):447-459.

[3] Zhang Y, Chiew F H S. Relative merits of different methods for runoff predictions in ungauged catchments [J]. Water Resources Research, 2009,45.

[4] 杨大文, 刘志雨, 张建云, 等. 中国的PUB科学问题和研究进展[C]∥ 全国第三届水问题研究学术研讨会. 西安, 2005:39-45.

[5] Parajka J, Viglione A, Rogger M, et al. Comparative assessment of predictions in ungauged basins-Part 1: Runoff-hydrograph studies [J]. Hydrology and Earth System Sciences, 2013,17(5):1 783-1 795.

[6] 杨大文, 夏 军, 张建云. 中国PUB研究与发展[C]∥ 第二届全国水问题研究学术研讨会. 北京, 2004:47-54.

[7] 徐 晶, 林 建, 姚学祥, 等. 七大江河流域面雨量计算方法及应用[J]. 气象，2001,27(11):13-16,51.

[8] 施 征, 包为民, 瞿思敏. 基于相似性的无资料地区模型参数确定[J]. 水文，2015,35(2):33-38.

[9] Lu H, Hou T, Horton R, et al. The streamflow estimation using the Xinanjiang rainfall runoff model and dual state-parameter estimation method [J]. Journal of Hydrology, 2013,480:102-114.

[10] 邓元倩, 李致家, 刘甲奇, 等. 基于SCE-UA算法新安江模型在沣河流域的应用[J]. 水资源与水工程学报，2017,28(3):27-31.

[11] 朱求安, 张万昌. 新安江模型在汉江江口流域的应用及适应性分析[J]. 水资源与水工程学报，2004,15(3):19-23.

[12] 王佩兰, 赵人俊. 新安江模型(三水源)参数的客观优选方法[J]. 河海大学学报，1989,(4):65-69.

[13] 赵人俊, 王佩兰. 新安江模型参数的分析[J]. 水文，1988,(6):2-9.

[14] Wang Y, Yu P, Yang T. Comparison of genetic algorithms and shuffled complex evolution approach for calibrating distributed rainfall-runoff model [J]. Hydrological Processes, 2010,24(8):1 015-1 026.

[15] 宋星原, 舒全英, 王海波, 等. SCE-UA、遗传算法和单纯形优化算法的应用[J]. 武汉大学学报(工学版)，2009,42(1):6-9,15.

[16] Duan Q Y, Gupta V K, Sorooshian S. Shuffled complex evolution approach for effective and efficient global minimization[J]. Journal of Optimization Theory and Applications, 1993,76(3):501-521.

[17] Duan Q Y, Sorooshian S, Gupta V K. Optimal use of the sce-ua global optimization method for calibrating watershed models [J]. Journal of Hydrology, 1994,158(3-4):265-284.

[18] Nelder J A, Mead R. A simplex-method for function minimization [J]. Computer Journal, 1965,7(4):308-313.

[19] Jeon J, Park C, Engel B A. Comparison of Performance between Genetic Algorithm and SCE-UA for Calibration of SCS-CN Surface Runoff Simulation [J]. Water, 2014,6(11):3 433-3 456.

[20] 马海波, 董增川, 张文明, 等. SCE-UA算法在TOPMODEL参数优化中的应用[J]. 河海大学学报(自然科学版)，2006,(4):361-365.

[21] 唐运忆, 栾承梅. SCE-UA算法在新安江模型及TOPMODEL参数优化应用中的研究[J]. 水文，2007,27(6):33-35, 74.

[22] 董洁平, 李致家, 戴健男. 基于SCE-UA算法的新安江模型参数优化及应用[J]. 河海大学学报(自然科学版)，2012,40(5):485-490.

[23] Madsen H. Automatic calibration of a conceptual rainfall-runoff model using multiple objectives[J]. Journal of Hydrology, 2000,235(3-4):276-288.

[24] Sobol I M. Sensitivity Estimates for Nonlinear Mathematical Models [J]. Mathematical Modelling and Computational Experiment, 1993,1(4):407-414.

[25] 齐 伟, 张 弛, 初京刚, 等. Sobol方法分析TOPMODEL水文模型参数敏感性[J]. 水文, 2014,34(2):49-54.

[26] Yatheendradas S, Wagener T, Gupta H, et al. Understanding uncertainty in distributed flash flood forecasting for semiarid regions [J]. Water Resources Research, 2008,44.

[27] 张小丽, 彭 勇, 徐 炜, 等. 基于 Sobol 方法的新安江模型参数敏感性分析[J]. 南水北调与水利科技，2014,(2):20-24,33.

[28] Sobol I M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates [J]. Mathematics and Computers in Simulation, 2001,55(1-3):271-280.

[29] Stein M. Large Sample Properties of Simulations Using Latin Hypercube Sampling [J]. Technometrics, 1987,29(2):143.

[30] Saltelli A. Making best use of model evaluations to compute sensitivity indices [J]. Computer Physics Communications, 2002, 145(PII S0010-4655(02)00280-12):280-297.

[31] 许崇育, 陈 华, 郭生练. 变化环境下水文模拟的几个关键问题和挑战[J]. Journal of Water Resources Research, 2013,(2):85-95.

[32] Parajka J, Merz R, Bloschl G. A comparison of regionalisation methods for catchment model parameters [J]. Hydrology and Earth System Sciences, 2005,9(3):157-171.