基于FPGA的小波变换边缘检测算法设计与实现
2018-05-28王智李扬陈鼎张晓栋陈少浩
王智 李扬 陈鼎 张晓栋 陈少浩


摘要:边缘是图像信息最集中的部分,而小波分析是近年来逐渐兴起的热门信号处理方法,其良好的时频局部分析的特性以及多尺度多分辨率思想在图像处理中具有高度的应用价值。提出了改进的小波边缘提取检测FPGA硬件结构优化算法,着重设计分析了小波变换FPGA VLSI电路结构,给出了一种9输入的并行计算电路,保证了少量像素点的边缘连续性,并在每级变换的高频运算中加入阈值截取,提取出更为精细的边缘曲线。该算法具有边缘提取计算速度快,调节阀值改变边缘提取清晰度等优点,具有广泛应用前景。
关键词:小波分析;FPGA加速计算;边缘检测
中图分类号:TP311 文献标识码:A 文章编号:1009-3044(2018)09-0261-04
Abstract: Edge is the most important part of the image information, and the wavelet analysis is emerging in recent years popular signal processing method, Its good time-frequency characteristics of local analysis and multi-scale multi-resolution ideas with high application value in the image processing. In this paper, based on the theory of wavelet transform, designed wavelet edge detection algorithm. Design based on FPGA is to focus on lifting wavelet transform VLSI circuit structure, proposes a parallel computing circuit of 9 input, guarantee a small amount of pixel edge continuity, and join threshold interception in the high frequency operation per level transform extract more elaborate edge curve. This algorithm has advantages of fast calculation, adjust edge clarity and etc, which has broad application prospects.
Key words: wavelet analysis; Accelerated computing; Edge detection
1图像边缘提取小波变换
将一个母函数进行平移、伸缩即可得到传统的小波函数,这种构造小波的方式是通过傅立叶变换完成。但在很多情况下,有些函数无法通过平移伸缩得到,因此难以用传统的小波变换对这些函数进行构造和分析。此外,传统小波变换是在实数域内作运算,在分析信号的过程中它们的小波系数也是实数。在小波变换应用层面越来越广时,就希望能在整数域内进行小波变换,即希望有“整数-整数小波变换”,小波系数为一系列整数序列,当然这种整数域内的小波变换依然必须是可逆的,具有该性质的小波变换我们称为整数小波变换,可用于构造整数小波变换,使小波分析的应用更为广泛。
提升方案通过进行预测和更新来分离信号的高低频分量,某点的信号值可根据局部信号间的相关性由其相邻的信号值经合适的预测算子来预测,预测所得到的值和真实信号的差值即为预测误差,将这个误差作为信号的高频信息,该过程即为预测环节。再将高频信息通过适当的更新算子得到低频信息,该过程即为更新环节。
以信号[X(n)]为例,其提升方案正变换过程如图1所示。下面为详细步骤介绍:
预测的目的是将数据表达的更加紧致,消除分裂后的冗余信息,是对变换的一个更新过程,并不是一个完整的等式。当[Xo(n)]完全可由[Xe(n)]预测,并且这个预测算子是相对理想的预测器时,可认为是理想预测,但在实际中,这种情况一般是不存在的。不过[Xo(n)]在和[Xe(n)]有较大的相关性时,预测后的新[Xo(n)]会具有很低的能量分布。
预测算子通常是多项式插值算式,并且预测是可逆的过程。若预测算子[p(.)]确定,就可以由[Xe(n)]和[d(n)]来恢复[Xo(n)],进而恢复[X(n)]。
综上所述,在提升方案中将实现小波变换分成了几个非常简单的步骤,这是提升小波的一大优点,其中每个步骤可以方便地找到相应的逆变换,小波逆变换即重构,就是分解的逆过程,只需改变数据的流向和运算符号就可以完成,相应的三个步骤即反预测、反更新和合并,如图2所示。
提升方案分解信号可达到和双正交小波变换相同的分解效果,因为可通过提升方案实现所有双正交小波。相比而言,提升方案是一种更加快速的算法,逆变换的实现同样比传统小波快很多。提升变换的另一个优点是其在整数域内完成变换,具有更好的实用价值。JPEG2000标准中,就通过提升算法来实现图像的二维可逆小波变换。
2 小波变换FPGA结构框架
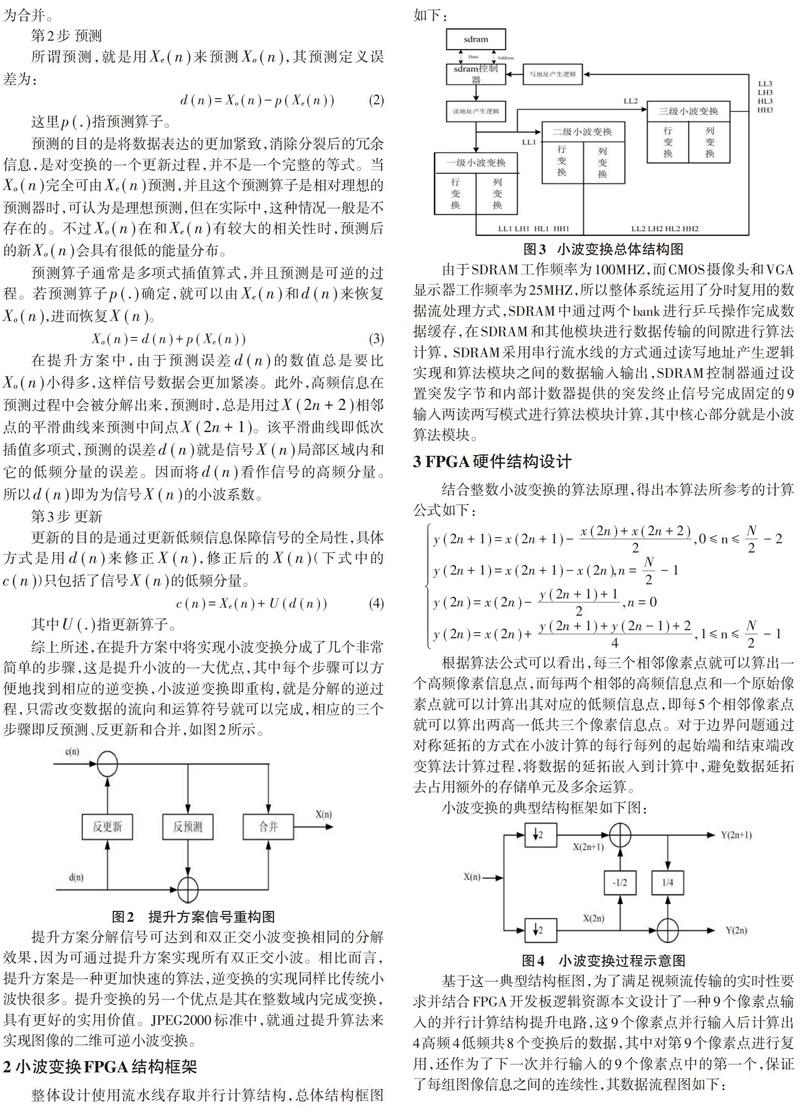
整体设计使用流水线存取并行计算结构,总体结构框图如下:
由于SDRAM工作頻率为100MHZ,而CMOS摄像头和VGA显示器工作频率为25MHZ,所以整体系统运用了分时复用的数据流处理方式,SDRAM中通过两个bank进行乒乓操作完成数据缓存,在SDRAM和其他模块进行数据传输的间隙进行算法计算, SDRAM采用串行流水线的方式通过读写地址产生逻辑实现和算法模块之间的数据输入输出,SDRAM控制器通过设置突发字节和内部计数器提供的突发终止信号完成固定的9输入两读两写模式进行算法模块计算,其中核心部分就是小波算法模块。
3 FPGA硬件结构设计
结合整数小波变换的算法原理,得出本算法所参考的计算公式如下:
根据算法公式可以看出,每三个相邻像素点就可以算出一个高频像素信息点,而每两个相邻的高频信息点和一个原始像素点就可以计算出其对应的低频信息点,即每5个相邻像素点就可以算出两高一低共三个像素信息点。对于边界问题通过对称延拓的方式在小波计算的每行每列的起始端和结束端改变算法计算过程,将数据的延拓嵌入到计算中,避免数据延拓去占用额外的存储单元及多余运算。
小波变换的典型结构框架如下图:
基于这一典型结构框图,为了满足视频流传输的实时性要求并结合FPGA开发板逻辑资源本文设计了一种9个像素点输入的并行计算结构提升电路,这9个像素点并行输入后计算出4高频4低频共8个变换后的数据,其中对第9个像素点进行复用,还作为了下一次并行输入的9个像素点中的第一个,保证了每组图像信息之间的连续性,其数据流程图如下:
根据以上结构,提升算法首先进行行变换,连续进行两次读操作,每次读9个数据,其中第一次读的第9个数据又是第二次读的第一个数据,首先计算高频,计算的结果将进行阈值截取,对于不满足阈值判定的高频数据赋0,阈值截取后的高频数据再进行低频计算,两次读共算出8高频8低频共16个数据,算完后再两次写数据将计算结果送回SDRAM存储。
行列变换都通过在读地址产生逻辑中定义横纵坐标读取数据,但是根据计算方式的不同讀取方式也不相同,行变换对图像逐行读取,而列变换首先读取第一行的前9个像素,再读取第二行的前9个像素,当读完最后一行的前9个数据后,再开始读第一行的9到18这9个数据,计算方式为竖向计算,计算电路依然使用图2-3、2-4的结构,由于列运算模块会使用一组寄存器专门存储当前的高频运算结果供下一组低频运算使用,因而列计算数据输入相互独立,相比图2-5的区别是每个计算模块的数据输入为独立的三根数据线。
行列计算结果通过写地址产生逻辑在SDRAM中存储,由于SDRAM的一个bank地址空间为[222],足够存储多幅640*480(系统级验证所采用的分辨率)大小图像,因而bank内部的地址读写实质上依然采用了乒乓方式,S为一帧图像像素点数目,当算完一帧后,数据存入SDRAM地址S到2S-1的范围内,二级变换后,又存到0到S地址范围内,覆盖原图像,以此类推。存储过程如下图所示:
根据上图可知,当需要进行多级变换时,只需要将LL部分读出,通过算法控制模块复用行列算法计算核,当正变换完成后就进行逆变换,逆变换为正变换的反操作,只需改变数据流向并将算法符号取反即可完成。
通过以上介绍可知,本文设计的硬件电路结构主要采用了流水线并行的办法,根据行列变换原理结合芯片资源进行设计,相比滤波器卷积的方式,计算量降低了一半,在提升算法中只用到了相乘和累加,而乘法都是2的倍数,用移位代替,实现过程中都是原位计算节省片上存储,并且提升小波的过程都是整数到整数的变换,易于硬件实现,相比依赖于傅里叶变换传统小波算法,优点较为突出。
4 FPGA软件优化设计
当存满一帧图像后,将图像数据输入算法模块进行算法运算。算法控制模块明确了算法的运行步骤,整体步骤是在初始化工作完成后先进行正变换的行列变换,再将算法中用到的计数器清零之后改变数据流向和运算符号,进行逆变换的列行变换,状态转换图如下:
再对提升小波的正变换进行设计,正变换的整体过程是对一帧图像完成行变换后再进行列变换,行列变换计算方式不同,分别调用了行列变换算法核。存取方式整体采用两读两写的模式,行列变换通过提供突发终止信号每次读9个数,这里要注意的是由于行列运算的不同(上一节已经提到),行计算步骤为“读、算、读、算、写、写”,列运算为“读、读、算、算、写、写”。由于采用的图像分辨率为640*480,加入了一个判断,如果在行首或者行尾的话,按照公式中的边界公式执行运算,两组数据共计算出8高8低共16个数据,存储后通过写地址产生模块写回SDRAM。
将以上步骤循环往复,可以完成计算一个行的小波变换,然后再进行下一行的小波变换,依次进行之后,当计算完480个行变换之后,这时一帧图像的行变换就结束了,接下来就可以开始列变换,下图为行列变换的状态转化图:
当行列变换完成之后,即第一级的小波正变换结束,本系统共需要进行三级的变换,即对以上的变换再进行两次,这里需要说明的是,第二次要变换的图像分辨率为320*240,做一次正变换可以将原始图像横竖划分为4份,左上角的部分为整个图像的低频区域,与其对称的右下角的图像为整个图像的高频区域。如果再要进行一次正变换的话,只需要对上一级正变换完的图像的左上角的低频区进行行变换即可,所以需要变换的图像分辨率为320*240.依此类推,第三次需要变换的图像分辨率为160*120。
三级正变换结束之后,接着就是小波变换的逆变换,逆变换在步骤上和正变换是一样的,区别在于公式的不同,所需变量的不同,其他的步骤都是相同的。通过每级不同的阈值设置,待三级的逆变换结束之后,就可以看到最后图像的边缘效果。
系统的验证平台采用ALERA公司的Cyclone IV 系列的EP4CE6F17C8开发板。算法的读写模块和正变化及逆变换模块共用同一个模块,缩小了FPGA逻辑资源的使用。以下表格是FPGA内部资源使用情况:
5 算法RTL级仿真结果及分析
系统仿真在计算机上实现完成,平台使用的是英特尔core i5处理器,仿真图如下:
图中sdram_dout即为txt文件图像数据输入,sys_data_in即为算法计算结果,之后将计算结果输出到一个txt文件上,再在MATLAB上合成图像,验证RTL级算法代码可行性。RTL级代码设计的变换级数为3级,下图左为原图,右为RTL代码边缘提取结果图:
进行了硬件电路的设计介绍以及算法各模块的设计仿真,最后给出了RTL代码的仿真边缘提取结果,从结果可以看到,小波的边缘效果连续并且通过阈值截取提出较为精细的边缘线条。
通过FPGA硬件模块并行处理的算法加速,很大程度上减少了图像经过小波变换计算的时间,通过用MATLAB仿真和FPGA硬件加速计算的结果对比可以明显看出差别:
有以上表格可见,当FPGA的工作频率在100MHz的情况下,对于不同分辨率图像进行小波变换边缘计算所耗费的时间,与MATLAB计算仿真所耗费的时间相比还是快了很多,在两个数量级以上。更关键的是,FPGA这个计算速度受到了SDRAM读写速度的限制,在将计算好的图像数据写入或者读出SDRAM的时候花费了大量的时间,如果刨除SDRAM读写的速度问题,可以更大程度上缩小小波变换边缘检测计算的时间。
参考文献:
[1] 鲍书朋.人工视觉假体系统设计[D].郑州大学,2014.
[2] Zrenner E. Will retinal implants restore vision Science,2002,295(8):1021-1025.
[3] 赵璨.应用于视皮层假体的图像处理系统的初步研究[D].重庆大学,2010.
[4] 谢程程.视觉假体图像处理策略及编码研究[D].上海交通大学,2011.
[5] Dagnelie G. Psychophysical evaluation for visual prosthesis[J]. Biomedical Engineering 2008, 10(1): 339.
[6] 李晟.视觉假体装置模型建立及视觉信息处理研究[D].上海交通大学,2011.
[7] 任秋实.视觉假体的研究进展与面临的挑战[A].生命科学,2009,21(2),235-240.
