库水位骤降作用下库岸滑坡形成机理研究

(1.上饶市鸿安水利水电勘测设计咨询有限公司，江西 上饶 334000；2.瑞昌市水利局，江西 瑞昌 332200)

20世纪以来，中国相继建设了一大批大型水电工程，其中大部分位于西南山区，如锦屏、二滩、小湾。大坝建成蓄水后，数百米的水位突升会严重威胁坝后库岸边坡的稳定性。此外，周期性的水位波动也会加重对边坡稳定的威胁。库岸边坡一旦失稳发生滑动，将会酿成不可预估的灾害。例如，1958年法国马尔帕塞水电站发生库岸滑坡，导致了下游区数百人员的伤亡[1-2]。2003年，发生在三峡库区的千将坪滑坡造成了20多人的伤亡以及长江航运的中断，经济损失严重[3]。因此，研究库岸边坡在库水位作用下的响应机制对其防灾减灾具有非常重要的意义。

根据朱冬林等[4]的调查结果，库岸滑坡主要发生在两个时期，即初次蓄水时期和库水骤降时期。巴亚东等[5]等研究了水位变化作用下，折线型黄土滑坡的失稳模式。贾逸等[6]研究了库水位升降对库岸边坡的影响。然而，针对库水位变化作用下，库岸边坡岩体饱和-非饱和转化以及渗流应力集中效应的研究相对较少。

本文结合非饱和土理论和有限元计算，考虑不同库水位工况作用下，库岸边坡渗流场及稳定的演化特征。并根据计算结果，分析库水位骤降对库岸边坡作用的机理。

1 基本计算理论

1.1 饱和-非饱和渗流理论

受到水电站调度的影响，水库水位周期性的波动造成库岸边坡岩土材料随时处于饱和-非饱和状态，其渗流特性与岩土材料的饱和度有很大关系。然而，基于质量守恒方程和达西定律可以得到如下所示的二维饱和非饱和渗流Richards方程[7]：

(1)

式中kx、ky——水平和垂直方向上的饱和土体渗透系数,m；

ρw——水的密度,kg/m3；

g——重力加速度,m/s2；

mw——比水容量，其物理含义是θω对基质吸力(ua-uw)偏导数取负数，见式(2)：

(2)

式中ua-uw——土体的基质吸力,Pa。

基于有限单元法可对式(2)进行计算，计算边界条件包括水头边界条件和流量边界条件，可参考罗红明[8]、刘新喜[9]等研究成果。此外，基质吸力作为一个重要的参数，对非饱和土体的工程性质具有重要影响，其基本的特征可以用土-水特征曲线来形容，主要反映基质吸力和含水率以及渗透系数的关系。通常来说，其关系可以通过经验公式拟合确定，常见的拟合模型包括Garder[10]、Van Genuchten[11]和Fredlund&Xing[12]等模型。本文选择较为常用的Fredlund&Xing模型，其计算公式如下所示：

(3)

式中Se——有效饱和度，Se=(θ-θr)/(θs-θr)；

h——基质吸力水头,m；

m、n、a——拟合参数；

同时本文对复杂圆弧点云进行了拟合。取直径为38 mm，直径偏差范围为0～0.5 mm的半段圆弧工件进行实验，如图3(a)所示为半段圆弧工件边缘外轮廓点云图，共包含98个边缘轮廓点。复杂圆弧点云中，噪声点较多且存在误差较大的点，同时点云并没有覆盖整个圆弧。如图3(b)所示为半段圆弧工件边缘外轮廓空间圆弧拟合图像。利用本文拟合优化法，对上述点云进行8次拟合，平均迭代数为3 026 次，拟合结果如表2所示。

θs——饱和含水率；

θr——剩余体积含水率；

θ——体积含水率。

1.2 边坡稳定计算

基于上述有限元方法可以确定边坡在库水位变化条件下的渗流场，同时，本文假设土体满足Mohr-Coulomb强度准则条件，然后基于简化Bishop法和简化的Janbu法确定边坡的稳定系数。

2 计算实例分析

2.1 计算模型

图1所示为一均质土坡，其材料计算参数[13]见表1。假设该边坡的初始蓄水位为25.00m，不同的水位下降工况见表2。基于Fredlund&Xing模型并参考经验取值(a=6.37;n=12.9;m=2.24)拟合确定基质吸力、渗透系数和含水量的关系(见图2)。

表1 计算参数

表2 水位运行工况

图2 土壤-水特征曲线

2.2 计算结果及分析

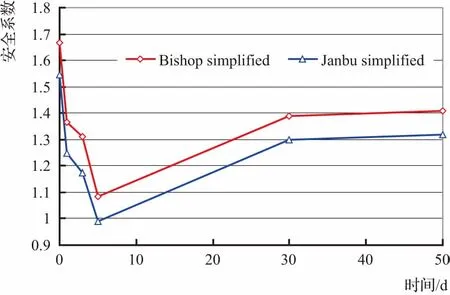
图3 工况1边坡安全系数演化过程

工况1的计算结果如图3所示。从图3中可以看出，库水位骤降能够明显威胁边坡的稳定，并且随着水位的不断下降，安全系数越来越低，但是随着库水位波动情况不断趋于平缓，安全系数会不断上升，直到逐渐稳定。

工况2的计算结果如图4所示。在该工况下，边坡的稳定趋势和工况1基本相似，但是存在两点明显差异。首先，水位第一次下降后，边坡在工况2条件下的安全系数(1.364，毕肖普算法)小于工况1条件下的安全系数(1.002，毕肖普算法)，即表明水位骤降速率越大，越能威胁边坡稳定；其次，由于工况2在第1～第3天存在一个稳定期，即水位没有波动，导致后期在相同水位波动情况下，工况2的安全系数明显高于工况1的条件，这表明库水位对边坡威胁存在一个累加效应。这也是导致工况2存在一个尖峰的原因。这为水电站调蓄带来了一个新思路：在相同时间、相同调度水位的情况下，期间保持水位尽量平稳过渡、降低调度速率，能够大大提高库岸边坡的稳定性能。

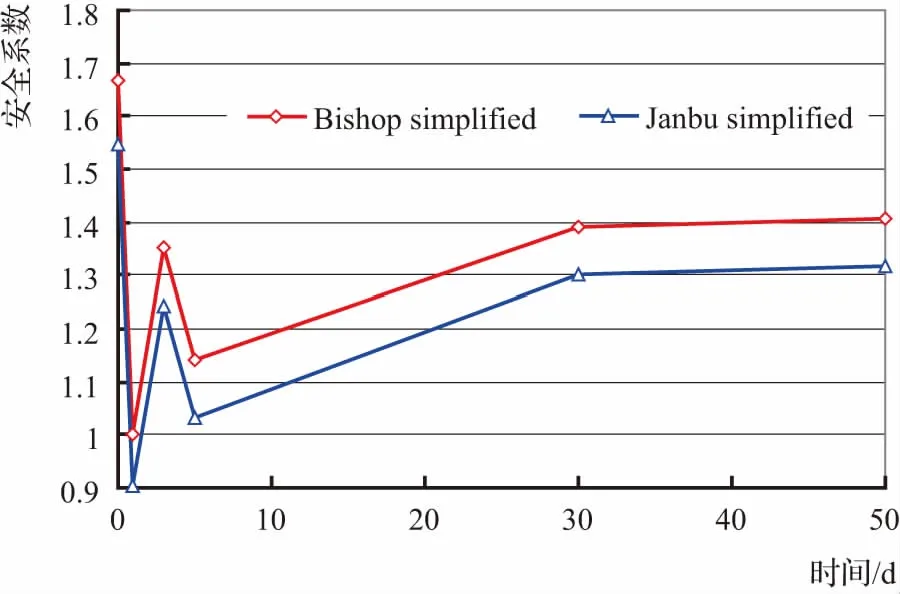
图4 工况2边坡安全系数演化过程

3 机理讨论分析

边坡滑动面孔隙水压的时空分布特征如图5所示。当库水位发生骤降后，边坡内部的孔隙水压会大幅度提高，而且孔隙水压的增加程度会随着水位波动的速率增大而增大，就是水位骤降速率越快，边坡的稳定性系数也越低的原因。同时，从图5中可以看出，随着水位不断下降，孔隙水压会不断升高，直到水位趋于稳定，并且经过一定的时期，孔隙水压才会逐渐消散。该结论能够很好揭示库水位对边坡的威胁存在累加效应的原因，这是由于在该水位稳定期间，为孔隙水压的消散提供了一个时机，减小了孔隙水压的积累。

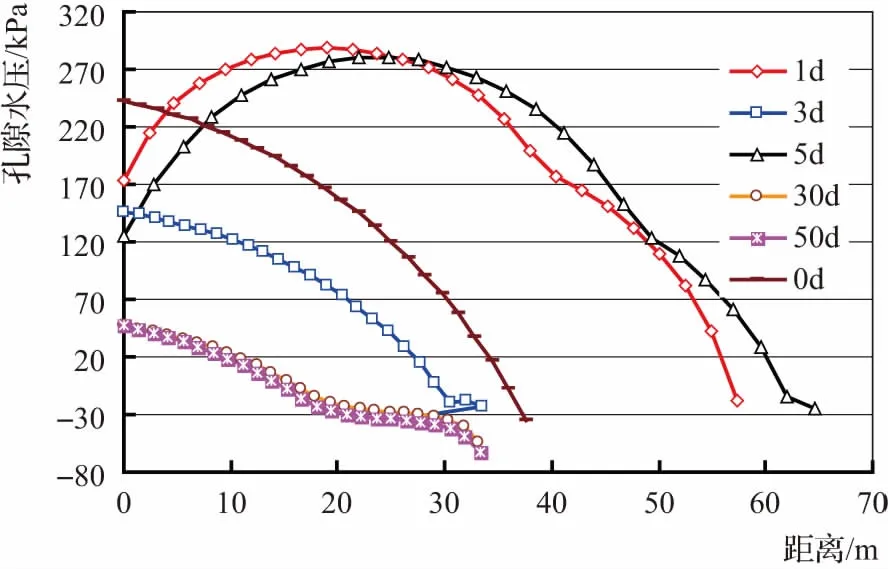
图5 孔隙水压时空演化特征

如图6所示，当水位发生骤降时，由于水头差会导致沿着滑动面方向形成一股渗流拖拽效应，并且水位骤降越快，渗流拖拽效应越明显，渗流拖拽效应也会随着库水位的稳定逐渐消失。值得注意的是，渗流拖拽效应不仅体现在增加额外的下滑力，还可能发生渗透破坏，导致边坡颗粒流失，由此带来边坡结构的改变。

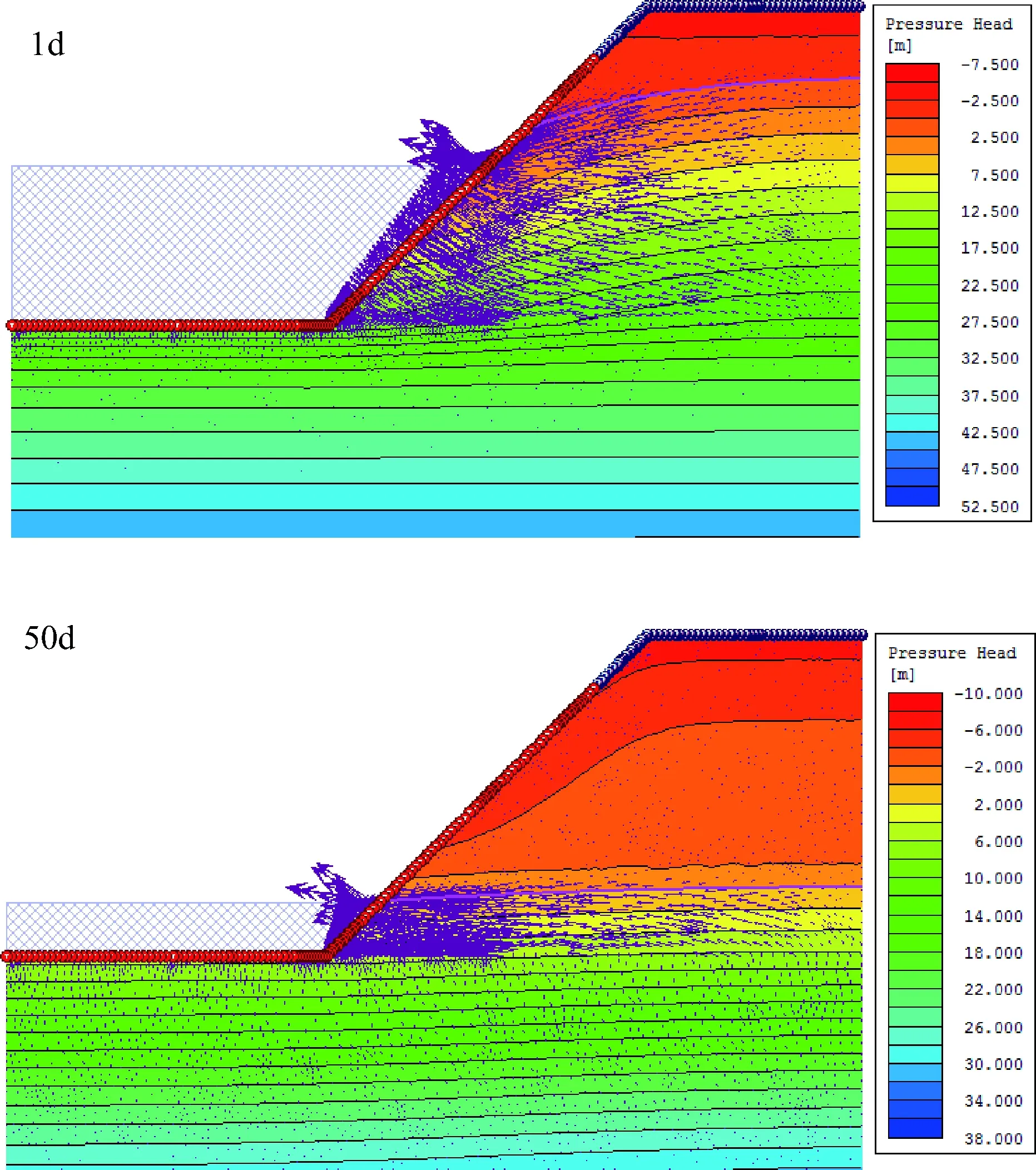
图6 边坡内部渗流方向演化特征

从应力状态来看，边坡在库水位骤降作用下，会引起边坡内部应力场的调整，从而适应当前荷载状态。边坡内部的剪切应力状态会随着库水位的骤降不断提高，并且会形成一个剪应力集中区域,如图7所示。从图7可以看出，一般应力集中会首先出现在滑动面剪出口，当该集中的剪应力超过边坡岩土材料抗剪强度时，就会导致该区域发生相对变形，从而造成局部破坏。如果库水位不断变化，该应力集中区域会逐渐向上、向内扩张，最终发生整体失稳。随着库水位波动逐渐稳定后，边坡的应力集中程度逐渐降低至正常值。

图7 剪应力时空演化特征

4 结 论

库水位下降会严重影响库岸边坡的稳定。本文基于饱和-非饱和土理论，采用有限元渗流分析，并结合边坡稳定系数计算的Bishop法和Janbu法，针对两种不同工况，确定了边坡在库水位骤降作用下的渗流和稳定演化过程。通过研究得出如下结论：

a.库水位下降会使得边坡的稳定系数降低，并且下降速率越快，稳定系数降低越多。此外，在水位下降过程中若存在水位平稳过渡区，边坡的安全系数能够有效得到提高。

b.库水位下降威胁边坡稳定的机理主要体现在孔隙水压激增，并且存在一个累加效应。此外，水位下降后带来的水头差引发了渗流拖拽效应，甚至可能导致渗透破坏。同时，库水位变化后，会在剪出口形成一个应力集中区域，并且随着库水位不断的波动，该应力集中区域会向坡体内部和上部扩张，最终诱发边坡整体失稳。

[1] Londe P.The Malpasset dam failure[J].Engineering Geology,1987,24(1-4):295-329.

[2] Petronio L,Boaga J,Cassiani G.Characterization of the Vajont landslide (North-Eastern Italy) by means of reflection and surface wave seismics[J].Journal of Applied Geophysics,2016(128):58-67.

[3] 殷跃平,彭轩明.三峡库区千将坪滑坡失稳探讨[J].水文地质工程地质,2007,34(3):51-54.

[4] 朱冬林，任光明，聂德新,等.库水位变化对水库滑坡稳定性影响的预测[J].水文地质工程地质，2002(3)：6-9.

[5] 巴亚东,杨秀娟,闫林,等.水位变化时折线型均质黄土岸坡失稳过程试验研究[J].水利与建筑工程学报,2016,14(3):182-185.

[6] 贾逸,任光明.某库岸滑坡在水库运行条件下稳定性的动态变化[J].水利与建筑工程学报,2011,9(5):24-30.

[7] 荣冠,张伟,周创兵.降雨入渗条件下边坡岩体饱和非饱和渗流计算[J].岩土力学,2005,26(10):1545-1550.

[8] 罗红明,唐辉明,章广成,等.库水位涨落对库岸滑坡稳定性的影响[J].地球科学:中国地质大学学报,2008(5):687-692.

[9] 刘新喜,夏元友,练操,等.库水位骤降时的滑坡稳定性评价方法研究[J].岩土力学,2005,26(9):1427-1431.

[10] Gardner W R.Some steady-state solutions of the unsaturated moisture flow equation with application to evaporation from a water table[J].Soil Science, 1958, 85(4):228-232.

[11] Genuchten M T V.A closed-form equation for predicting the hydraulic conductivity of unsaturated soils.[J].Soil Science Society of America Journal,1980,44(44):892-898.

[12] Fredlund D G,Xing A.Equations for the soil-water characteristic curve[J].Canadian Geotechnical Journal,1994,31(4):521-532.

[13] 童富果.降雨条件下坡面径流与饱和-非饱和渗流耦合计算模型研究[D].宜昌：三峡大学,2004.

[14] Yin,Y.,Huang,B.,Wang,W.,et al.Reservoir-induced landslides and risk control in three gorges project on yangtze river,china[J].Journal of Rock Mechanics and Geotechnical Engineering,2016,8(5):577-595.

[15] 王明华,晏鄂川.水库蓄水对库岸滑坡的影响研究[J].岩土力学,2007,28(12):2722-2725.

[16] 康锋,陶春洁,李志强.水位降落期堤防上游边坡抗滑稳定初步研究[J].水利建设与管理,2016,36(5):22-24.

[17] 李世娟.小型水库土石坝稳定分析[J].水利建设与管理,2015,35(3):27-29.