流态软土管道的流动试验及其本构方程

马誉鑫,殷德顺



流态软土管道的流动试验及其本构方程

马誉鑫,殷德顺*

河海大学力学与材料学院, 江苏 南京 210098

为解决盾构出土、基坑开挖等工程中高含水量软土在管道中的运输问题，本文参照高聚物流体管道流动性质，设计适用于流态软土管道流动性质的仪器，并通过分析管道中流动的高含水量软粘土，发现其剪切粘度符合幂律关系；通过对不同长径比流态软土的剪切应力-应变率曲线的拟合，得到含水量与剪切速率的拟合公式，拟合曲线的指数均在0.25左右，方程系数均比较接近。该方程能够用于计算流态软土的剪切应力，为工程应用提供方便。

管道; 软粘土; 流动试验; 本构方程

随着近年来中国经济的发展，国家对于环境保护的意识不断增强，地方上各部门的监管强度日益提高，大量高含水量流态软土作为建筑废弃物，不能随意倾倒与丢弃，因而软粘土的运输便成为了一个重要问题。管道运输不仅能减少污染，还能提高输送效率，也有助于缓解交通紧张等问题。因此，软土地区隧道及深基坑开挖、淤泥清理过程中，需要充分掌握管道中软土的力学特性，以便更高效地进行泥土管道运输。

对于管道运输而言，研究多集中在淤泥和污泥等方面。肖海文[1]研究了大管径排水管道的清淤效果，并对其输送效率进行了分析。吴淼[2]通过对城市污泥的流变特性和输送特性试验分析污泥在管道中的阻力损失与输送距离及流量之间的关系。陈志平[3]研究了管道中的污泥输送，但污泥中的含水量过高，与以往的软土管流不同。张晓斌和冯民权[4,5]研究了利用小型污泥流动试验装置，对脱水污泥流动阻力特性进行探讨。但研究对象的淤泥和污泥的含水量在80%以上，其研究仪器不能直接应用于工程中所面临的高含水量土体的研究。所以有必要设计软粘土管道流动试验来研究流态软土管道运输。

软土管道运输距离往往较长，研究软土在管道运输中的流动性质能够为其如何降低阻力提供依据，鉴于软土力学性质的复杂性和目前工程上出现的众多问题，有必要充分掌握软土在管道中流动的力学性质并进行本构方程的相关研究，为工程提供运输效率较优的参数，控制较少的参数达到更高效地进行软土管道运输的目的，为研究流态软土的力学模型提供依据。

基于固体力学基础的土体力学模型有很多种类，如经典的库伦摩尔模型、邓肯-张（双曲）模型、超弹性模型等。相比较而言，以流体力学为基础的本构模型就相对稀少很多。1970年美国地质地貌学家Johnson[6]提出有关于泥石流的运动模型，并基于宾汉粘性流模型建立了泥石流运动方程[7]。国内外许多学者基于该模型对泥石流的运动方程进行了研究和改进。日本泥石流学家Takahashi教授[8]，通过对平均粒径为0.15 mm微粒的水槽实验，实验中对剖面垂直方向的速度分布进行了研究，提出用膨胀流来模拟泥石流Liu[9]基于前人提出的流变模型，将其为两部分并进行修正。Pudasaini[10]提出了一种广义两相泥石流模型，考虑了粒子间流体动量的作用。Luna[11]基于超孔隙水压力和极限平衡的物质夹带过程提出了一维泥石流模型。Kalyon[12]和Kaftori[13]开展了非牛顿流体阻力特性的研究。陈育民[14]根据其对土体进行液化后扭剪试验提出：在零有效应力状态下，饱和砂土呈现剪切稀化非牛顿流体的性状，可以用幂律函数来描述剪切稀化状态下的剪应力—剪应变关系。关于流态软土本构方程的研究并不多，因此研究流态软土管道运输的本构方程具有十分重要的工程意义。

为了研究流态软土在管道运输中的流动性质，本文设计了用于研究软粘土管道流动性质的仪器，采用实际工程中常用的软土作为试验对象，研究了软土剪切流动的本构方程，旨在为软土输送管道的运行参数优化提供依据。

1 试验设计

软粘土管道流动试验借鉴了高分子聚合物研究仪器以及其研究剪切流动的方法。根据流体力学的相关理论，设计试验分析软土流动状态下的剪切应力和剪切应变率关系。

试验装置由压力容器、活塞、不同长径比管道、土压力传感器等部分组成。为了研究软土在管道中的流动性质，设计了总共三种不同长径比管道。试验筒（压力容器）如图1所示。

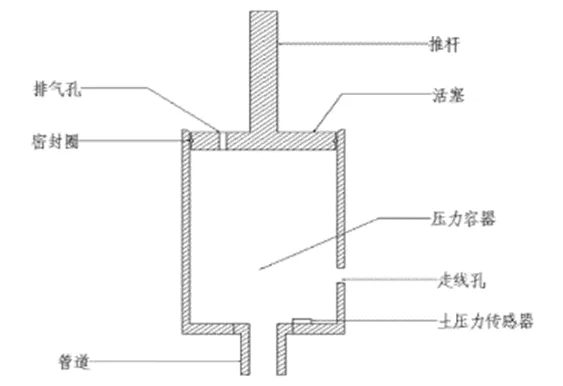
图 1 试验筒结构示意图

试验仪器主体为表层镀锌的圆柱形铁质筒体容器，主尺寸为：内径199 mm，高380 mm。筒体侧壁下侧开有直径10 mm的圆孔，让传感器可以走线。压力容器底部的中心有直径为70 mm的孔，孔壁上有螺纹，可以接不同直径管道，试验管道长度内径尺寸分别为20 mm，36 mm，52 mm，长度均为110 mm，对应管道长度下的长径比分别为5.5，3.06，2.12。

试验中采用伺服机进行等应变加载方案将软粘土挤出，加载速率分别为10，20，30，40，50，60 mm/min。伺服机的加载速率即为流态软土在管道中的平均流速。配制的软土含水量分别为40%，45%，50%，55%。试验土样取自南京秦淮河河床，除杂后通过干燥、研磨和筛分等过程后得到。

试验中，通过土压力传感器测得管道入口处土体压强差△，管壁处的软土剪切应力为：

式中τ为软土剪切应力，kPa；表示管道长度，mm；D表示管道直径，mm。

2 试验结果与分析

2.1 剪切应力与剪切粘度关系

试验所用的具有一定含水量的软土，是由研磨过筛后细小的粘土颗粒加水配制而成，基本上是呈非沉降性的均质浆体。殷德顺[15]等人的试验研究表明，流态土属于剪稀流体，其粘度会随流动速度增加而减小。流速比较低时，曲线的减幅较大，说明软土的粘度会很高，所受到的阻力也会比较大。利用软土剪切流变曲线，可以进一步得到软粘土剪切粘度随剪切速率变化的曲线，如图2所示。

从图2中可以看出，随着剪切速率的增加，软土剪切粘度下降明显。在开始段剪切速率较低时，软土剪切粘度随剪切速率迅速下降，随着剪切速度进一步增加，曲线下降幅度趋缓，说明其剪切应力破坏了软土的原有结构，流动阻力变小，软土表现的流动性更佳，当流速继续增大到一定数值时曲线与横坐标趋于平行，说明软土管道流动的阻力最终逐渐趋于稳定。

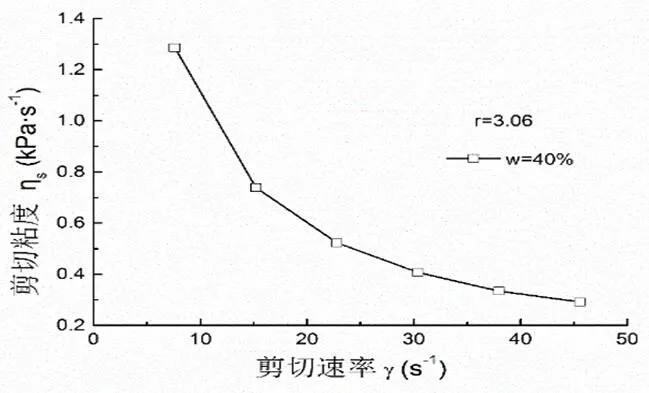
图2 长径比为3.06时的剪切粘度-剪切速率曲线

2.2 软粘土剪切粘度谱

剪切粘度是影响粘性流体管道流动性能的重要参数。软粘土的剪切粘度，即为软粘土在流动过程中所受到的剪切应力与剪切速率的比值。因为软粘土是假塑性流体，其流动行为具有剪切变稀的特性，通常需要利用剪切粘度与剪切速率的关系曲线，即剪切粘度谱来全面反映软粘土管道中的流动特性。

长径比为3.06时软粘土的剪切粘度谱如图3所示，长径比为5.5时软土剪切粘度谱对数图像如图4所示。从图中可以看出，同一含水量下的软土，其剪切粘度随剪切速率的增大而减小。含水量较低时，软粘土剪切粘度较高，剪切速率对软粘土剪切粘度有较大的影响。含水量较低高时，剪切速率对软粘土剪切粘度的影响比较小。当软粘土含水量增大到55%左右时，软粘土剪切粘度-剪切速率曲线趋近于一条水平直线，说明高含水量下软粘土剪切速率对剪切粘度影响非常有限。在相同剪切速率时，软粘土剪切粘度随含水量的增大而显著减小。而且，在低剪切速率下，这种现象更加明显。其剪切粘度对数曲线为相互平行的直线，与高聚物的剪切粘度对数曲线相互平行的结果相吻合。

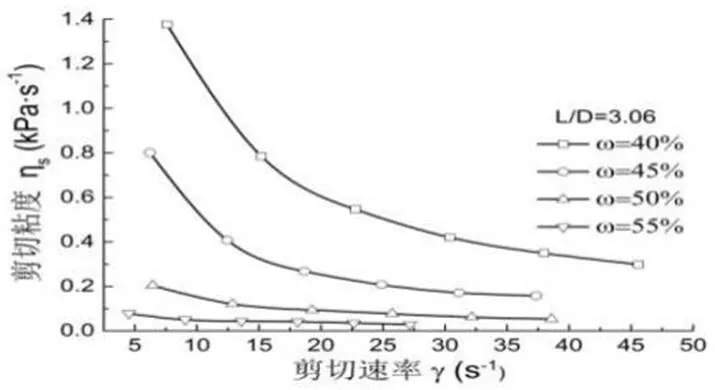
图3 长径比为3.06时的软粘土剪切粘度谱

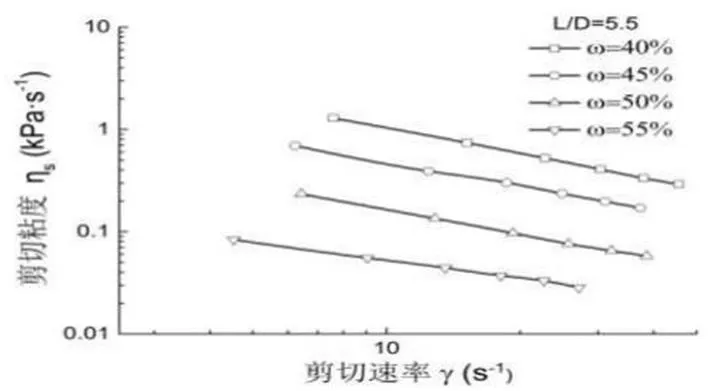
图4 长径比为5.5时的软粘土剪切粘度谱对数图像

2.3 软粘土剪切流动本构方程

根据对高含水量软粘土特性概述的理论分析，可以得出软粘土的主要流动特性：软粘土基本上是呈非沉降性的均质浆体流动，且具有明显的粘弹性流变特性，可以视为非牛顿流体。在某一长径比输送管道中，对应于不同的含水量，软粘土有着截然不同的剪切应力-应变率曲线。这就导致了描述流态软粘土流动特性的方程过多，不利于计算。由试验得到的流态软土剪切粘度-应变率曲线（图2）可以看出，试验所研究的高含水量软粘土属于非牛顿流体，符合非牛顿流体的特性，需要通过构建一个本构方程来验证试验得到的曲线，笔者通过比较各种模型的拟合效果，最终选择并建立了幂律流变模式的三参数方程，用以表征不同含水量的流态软土剪切应力-应变率关系。

幂律流变模型的本构表达式为：=()(3)

式中为剪切应力，为剪切粘度，为剪切速率，为非牛顿指数。

笔者将即软粘土剪切粘度视为随剪切速率变化的函数，将不同含水量软粘土剪切粘度-剪切速率曲线对数图像在轴上的截距0视为随含水量变化的函数，利用幂律流变模型描述流态软土的剪切应力—应变率关系。

假设剪切应力与剪切速率的拟合关系式为：=ae-1·(4)

式中系数，为常数，的指数-1，表示为曲线的斜率，其中为非牛顿指数。随着值的增大，非牛顿效应减弱，材料的粘弹性也减弱。为了将简化各条拟合曲线以得到一个含参数较少的关系式，笔者利用剪切粘度谱来进行计算，将近似平行的四条软粘土剪切粘度-剪切速率曲线作平行处理后，得到指数的平均值。不同长径比下本构方程拟合结果见表1，取其中三条曲线进行拟合，剩下的一条进行验证，发现其拟合结果较好。

表1 拟合结果

3 结论

为了研究软粘土管道流动力学性质，笔者从流体力学研究角度出发，利用改进毛细管试验仪得到的软粘土流动试验仪器，研究了流态软土剪切流动特性及其本构方程，得到如下结论：

（1）高含水量软粘土是一种非牛顿流体，软粘土剪切粘度随剪切速率的增大而迅速降低，软粘土剪切粘度—剪切速率的对数曲线近似直线，且不同含水量下的软粘土剪切粘度—剪切速率的对数曲线近似平行。

（2）通过分析管道中流动的高含水量软粘土，发现其剪切粘度符合幂律关系，其剪切应力—应变率曲线符合幂律流变模型，通过对不同长径比软粘土的剪切应力-应变率曲线的拟合，得到了两参数拟合公式，参数只有含水量与剪切速率。

（3）对于不同长径比的情况，笔者拟合出的曲线的指数均在0.25左右，方程的系数均比较接近，符合实际，具有一定的通用性。通过与试验结果的比对分析，能够发现此拟合公式的拟合结果具有较好吻合度，能够被用于计算软粘土的剪切应力，为工程应用提供了方便。

[1] 肖海文,朱林海,翟俊,等.一种新型大管径排水管道清淤装置[J].中国给水排水,2013,29(20):140-144

[2] 吴淼,赵学义,潘越,等.城市污泥的特性及管道输送技术研究[J].环境工程学报,2008,2(2):260-265

[3] 陈志平,谢淮明,宋旭,等.脱水污泥管道输送阻力计算模型对比研究[J].中国给水排水,2016,32(3):101-103

[4] 张晓斌,冯民权,张丽.污泥壁面滑移特性检测研究[J].西安理工大学学报,2011,27(2):200-204

[5] 张晓斌,冯民权,谭未,等.污泥在排污直管内的流动阻力特性研究[J].西北农林科技大学学报:自然科学 版,2013,41(9):214-220

[6] Johnson A, Rahn P. Mobilization of debris flows[J]. Zeitschrift fur Geomorphologie, 1970,9:168-186

[7] Johnson A. A model for grain flow and debris flow[R]. Denver:U. S. Department of the Interior U. S. Geological Survey, 1996

[8] Takahashi T. Debris flow on prismatic open channel[J]. Journal of the Hydraulics Division, 1980,106(3):381-396

[9] Liu KF, Huang MC. Numerical simulation of debris flow with application on hazard area mapping[J]. Computational Geosciences, 2006,10(2):221-240

[10] Pudasaini SP. A general two‐phase debris flow model[J]. Journal of Geophysical Research: Earth Surface, 2012,117(F3):1-28

[11] Luna BQ, Remaître A, Van Asch TW,. Analysis of debris flow behavior with a one dimensional run-out model incorporating entrainment[J]. Engineering geology, 2012,128(2):63-75

[12] Kalyon DM. Apparent slip and viscoplasticity of concentrated suspensions[J]. Journal of Rheology, 2005,49(3):621-640

[13] Kaftori D, Hetsroni G, Banerjee S. The effect of particles on wall turbulence[J]. International Journal of Multiphase Flow, 1998,24(3):359-386

[14] 陈育民,高星,刘汉龙.砂土液化流动变形的简化方法[J].岩土力学,2013,34(6):1567-1573

[15] Yin D, Duan X, Zhou X,. Time-based fractional longitudinal-transverse strain model for viscoelastic solids[J]. Mechanics of Time-Dependent Materials, 2014,18(1):329-337

The Flow Experiment and Constitutive Equation of Flow Soft Clay in Pipeline

MA Yu-xin, YIN De-shun*

210098,

To solve the convey problem for soft clay in pipeline in shield tunnel excavation and deep foundation pit excavation etc. This paper referred to the flow properties of high polymers in pipeline to design the instrument to suit for the transportation of flow soft clay in pipeline and find the according relationship between shear viscosity and power law by way of flow analysis on high water soft clay. The fitting formula of water content and shearing rate was gotten from simulation of the shear stress and strain rate curve of soft clay at different draw ratios, the exponential ofwas about 0.25, the coefficients of equations were relatively close. The formula could be used to calculate the shear stress of soft clay and provide a convenience for the engineering application.

Pipeline; soft clay; flow experiment; constitutive equation

TU411

A

1000-2324(2018)03-0514-04

2017-04-12

2017-05-06

马誉鑫(1994-),男,硕士研究生,主要研究方向为软土的力学与工程特性. E-mail:yuxinma@hhu.edu.cn

Author for correspondence. E-mail:yindeshun@hhu.edu.cn