日立ARIETTA60超声成像系统成像功能的一种预防性维护方法
2018-05-26任莉莉杨曦杨佳王宏权蔡兴文
任莉莉,杨曦,杨佳,王宏权,蔡兴文
丰都县人民医院 a.设备科;b.内分泌科;c.泌尿外科;d.功能科室,重庆 408200
引言
医学超声成像系统是开展诊疗活动的重要设备,很多医院为确保其安全有效地运行,进行整机除尘、连接件检测、电气安全检测、图像质量评价等等预防性维护工作[1-3]。其中,图像质量评价借助专门的仿组织体模完成盲区、分辨率、探测深度、测量偏差等等客观数据的检测[4-5],而成像结果有无偏差仍是主观判断。若成像部件出现老化或其他的问题,检测的客观数据前后结果一致,检测者肉眼也没有发现的明显差异,认定超声成像系统没有问题,无法及时维护维修,使得小问题扩大,增加后续的维护维修成本,同时,影响诊断结果。我们以日立ARIETTA 60超声成像系统为研究对象,建立其成像功能的预防性维护模型,实现成像结果客观的检测,希望及时客观地维护处理超声成像系统。即发现超声图像的信噪比呈正态分布,建立3组正常成像的超声图像信噪比数据为配对样本组的配对样本t检验模型,对某时段的信噪比数据组进行检测,若检测结果显示检测样本与配对样本属于同一总体则说成像功能正常,若结果表明不属于同一总体则说明成像功能可能出现问题,需要进一步检查维护。
1 方法
1.1 信噪比
信噪比是客观评价图像质量的常用指标之一,该指标越高表示原始信号越多,噪声越小,图像质量越好,越有利于诊断,其公式如下:

其中,f(i,j)是不含噪声的原始图像,g(i,j)是图像中噪声,Row×Col表示图像行列,SNR的单位是db[6-8]。我们获得的超声图像都是含有噪声的h(i,j),即:
h(i,j)=f(i,j)+g(i,j),对公式(1)作如下变化:
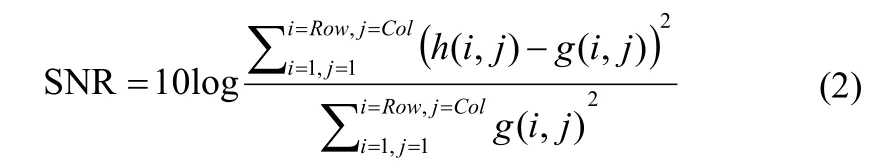
噪声估计使用经典小波变换的硬阈值法,即将图像进行小波变换,将小波系数的绝对值与所选定的阈值λ进行比较,小于或者等于阈值的收缩值为零,大于阈值则保持变,其公式如下:
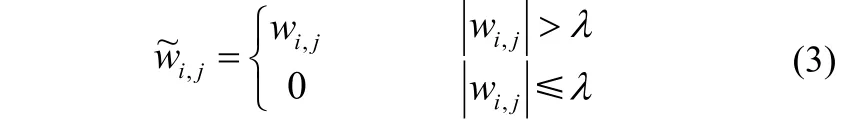
其中,是估计噪声标准差,是最高分辨级I-1的小波系数,“median”表示序列按照大小顺序排列后的中值[9]。将处理的小波系数进行逆变换估计原始图像f(i,j),再与我们直接取得含有噪声的图像h(i,j)相减得g(i,j),即g(i,j)=h(i,j)-f(i,j)。
编译平台为Matlab 2010a。日立ARIETTA 60超声成像系统生成的超声图像含有检查区域和黑色区域,黑色区域是我们所不需要的,所以我们需要对分析的区域进行选择。在Matlab平台上,使用GUI工具箱制作能读取超声图像、选择感兴趣区域、以公式(1)和(2)为基础计算信噪比,并且能在Windows系统下运行的应用程序。
1.2 统计检验模型
超声成像系统是以一种固定方式成像,但成像过程受到被检查者的体质、检查部位、天气、操作者的手法等相互独立随机因素的影响,使得成像过程随机化,超声图像是一个随机结果,用同一公式估算的信噪比也是一个随机变量。在实际情况中,由相互独立的随机因素综合影响形成的随机变量服从正态分布[10],所以我们假设日立ARIETTA 60超声成像系统生成超声图像的信噪比呈正态分布,即所有信噪比是一个总体,且是一个随着时间延长,个体不断增多的总体(时间越长,检查的人次越多,生成的超声图像越多,得到信噪比个体越多,总体随之不断增大)[11-12]。
1.2.1 样本
我们希望能在时间轴上检测日立ARIETTA 60超声成像系统成像功能的运行情况,所以以某天前15个超声图像的信噪比为1个样本,以便能准确找到出现故障的时间,回忆当天的情况找出故障原因。按照上述方法分别抽样2017年3月22日、2017年3月30日和2017年3月31日的超声图像信噪比,分别记为A、B、C组。其中,信噪比的计算必须由同一人进行,否则会因为人为因素影响结果。
1.2.2 模型建立
检验平台为SPSS 17。Kolmogorov-Smimov检验(简称KS检验)能描述两个独立统计样本的相似性[13],检测数据是否符合正态分布。在SPSS软件上检测3组数据是否呈正态分布,若检验结果大于等于0.05,则说明数据组是正态分布;若小于0.05,则说明数据组不是正态分布。经过检验分析,3组数据都符合正态分布,说明日立ARIETTA 60超声成像系统的超声图像信噪比呈正态分布,可以建立以此3组数据为配对样本组的配对样本t检验模型,检测某时段的抽样样本与配对样本组是否属于同一总体来判断此期间成像功能是否出现问题。若检测结果大于等于0.05,则抽样样本与配对样本组属于同一总体,说明信噪比分布一致,成像结果的分布一致,成像过程一致,即设备一直按照某种随机规律成像,并没有受到不良因素破坏成像过程,换言之就是成像功能在期间一直正常;若检测结果小于0.05,说明不属于同一总体,信噪比分布规律不一致,成像结果分布一致,成像方式不一致,即有可能成像功能出现问题,需要进一步检查设备。
1.2.3 模型验证
抽样本设备2017年7月15日的信噪比为正常样本,记为D组。由于我院2016年12月底购买,至今无任何故障问题,所以抽样同一厂家同一系列不同型号的日立ARIETTA 70超声成像系统2017年3月10日的信噪比样本作为故障组,记为E组。分别将D、E组分别与配对样本组进行配对样本t检验,以验证模型是否可行。若D组的所有检验结果大于等于0.05,且E组的检查结果不是所有都大于等于0.05,即是正常样本与配对样本组服从同一正态分布,是同一总体,成像过程相同,故障样本与配对样本组不属于同一总体,成像过程不相同,检测结果与抽样事实完全相符说明本模型可行,能通过检测指出成像过程是否出现问题。若检测结果出现其他情况,说明与事实不完全相同,本模型不可行。
2 结果
2.1 信噪比结果
读取超声图像的显示情况,见图1。选取计算区域放大,并显示计算结果的图像,见图2。其中,图2所示结果与后序统计的数据无关。估算的ARIETTA60超声成像系统图像信噪比的结果,见表1。
2.2 检验结果
用KS检验ARIETTA 60超声成像系统图像信噪比与正态分布相似度的结果,A、B、C三组的结果分别为0.838、0.540和0.982。结果远远大于0.05,表明ARIETTA 60超声成像系统生成超声图像的信噪比呈正态分布,可以使用正常运行下生成超声图像的信噪比作为模板,将某时段的图像信噪比进行配对样本t检验,检测是否属于同一总体来说明设备是否一直正常运行。

图1 载入后界面
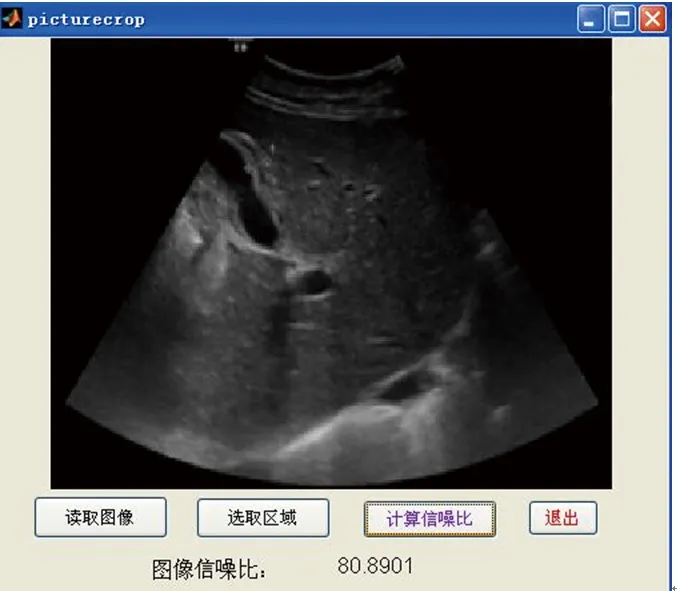
图2 选取计算区域及结果
将3组数据两两进行配对样本t检验。若检验结果大于等于0.05,说明数据组都来源于同一总体;若小于0.05,说明数据组不来源于同一总体。A组与B组为0.754,A组与C组为0.795,B组与C组为0.825。表明这3组数据是属于同一总体,进一步证实ARIETTA 60超声图像信噪比是呈正态分布,说明可以用检测时段的信噪比与正常情况下的样本进行检测方法来判断设备的运行情况是否正常。
验证组的信噪比估算结果,见表2。与配对样本组的检测结果,见表3。结果表明,D组与配对样本组属于同一总体,与事实相符;E组与配对样本不属于同一总体,也事实相符;说明本模型能用于检测ARIETTA 60超声成像系统成像功能是否正常。

表1 ARIETTA60超声成像系统图像信噪比估算结果

表2 验证组的信噪比结果

表3 验证组与配对样本组的检验结果
3 结论与讨论
上述结果表明,可以建立统计检验模型对ARIETTA 60超声成像系统的成像功能进行预防性维护,但是必须有至少3个以上正常运行的配对样本组,才能保障检测结果的准确度,尽可能地不出现第二类错误。其中,E组与B、C组符合同一正态分布的原因可能是由于两台设备都属于同一生产厂家同一系列的产品导致,或者是超声图像信噪比的分布相似度比较高所致,需要进一步研究分析。早在2003年,高洪青[14]的研究中就表明统计检验模型可以用于监测设备运行情况,且有很多相应的后续报道。本文与胡蜂等[15]、侯澍旻等[16]的研究报道所提的KS检验的相似度模型相比,提出是否属于同一总体的检验模型要更加准确。且本方法无需借助仿生组织体模进行检测,节约一笔不小的支出和后续对仿生组织体模的维护费。此模型有一定的局限性,目前只针对日立ARIETTA 60超声成像系统,要同一个人对信噪比进行统计。本文所提的方法为超声系统成像的预防维防提供一种新思路,希望在后期的努力,和各位同行的帮助下能改善其局限性。
[参考文献]
[1] 赵坚.超声诊断仪器的预防性维护与故障解决方案[J].中国医药导报,2015,(16):165-168.
[2] 周嫱.超声诊断仪的预防性维护探讨[J].中国医疗设备,2013,28(11):156-157.
[3] 王功华,张平.超声诊断仪器的预防性维护[J].中国医疗设备,2012,27(1):104-106.
[4] 姬军,潘美玲,张春霞.超声图像的质量评价[J].医疗卫生装备,2012,31(12):4.
[5] 官辉煜.超声图像质量检验系统设计的评估[J].中国医疗器械信息,2010,16(11):36-42.
[6] Pauluzzi DR,Beaulieu NC.A comparison of SNR estimation techniques for the AWGN channel[J].IEEE Trans Commun,2002,48(10):1681-1691.
[7] Romero-Laorden D,Villazón-Terrazas J,Martínez-Graullera O,et al.Strategies for hardware reduction on the design of portable ultrasound imaging systems[M].Stamford:InTech, 2013.
[8] 陆玉婧.超声图像降噪去斑算法研究[D].昆明:云南大学,2014.
[9] 孙延奎.小波变换与图像、图形处理技术[M].北京:清华大学出版社,2012:156-157.
[10] 盛骤,谢式千,潘承毅.概率论与数理统计[M].北京:高等教育出版社,2008:147.
[11] 周勇,肖冰.基于OMP算法的超声图像重建特性研究[J].计算机技术与发展,2017,27(7):135-139.
[12] 郑渊悦,徐铭恩,王玲.改进权值非局部均值超声图像去噪[J].中国图象图形学报,2017,22(6):778-786.
[13] 吴善元,王兆军.非线性统计方法[M].北京:高等教育出版社,1996:144-150.
[14] 高洪青.基于概率模型的设备状态自适应评估与预测技术[D].西安:西安交通大学,2003.
[15] 胡峰,吴波,胡友民,等.基于概率神经网络和KS检验的机械状态监测[J].振动与冲击,2008,27(4):56-57.
[16] 侯澍旻,李友荣,姬水旺等.基于KS检验的智能故障诊断方法研究[J].振动与冲击,2006,25(1):82-85.
