汽车主减速器弧齿锥齿轮参数化设计方法研究

王科银，苗振华，刘仲阳，寇满

（1.湖北汽车工业学院汽车工程学院，湖北 十堰 442002；2.吉林大学汽车工程学院，吉林 长春 130012；3.海马（郑州）汽车有限公司，河南 郑州 450016；4.郑州宇通客车有限公司，河南 郑州 450016）

1 概论

汽车单级主减速器具有结构紧凑简单，体积和质量较小，而且制造成本便宜等优点，因此被广泛应用于主减速比i0≤7.6的各种中、小型汽车上。在现代汽车驱动桥上，“格里森”（Gleason）制或“奥利康”（Oerlikon）制螺旋锥齿轮是被应用最为广泛的主减速齿轮种类，即本文所研究的弧齿锥齿轮。本研究的重要意义在于，借助CATIA计算机辅助设计技术实现对弧齿锥齿轮全部参数化精准建模，比之前的传统方法提高了设计工作效率、设计质量并且缩短了产品开发周期，这对锥齿轮设计产品系列化具有非常重要的工程实际意义。

2 弧齿锥齿轮主要结构参数

弧齿锥齿轮主要结构参数如表1所示：

3 弧齿锥齿轮理论方程

3.1 弧齿锥齿轮球面渐开线方程

弧齿锥齿轮的球面渐开线MP点的齿廓的直角坐标参数化方程为：

表1 弧齿锥齿轮主要结构参数

式中：

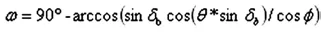
ω--矢径对Z轴的夹角，σ--矢径在XOY平面的投影与X轴的夹角，σ=θ-φ δb--基锥角

θ--发生面与基锥底圆切点的展开角

φ--矢径在 XOY平面的投影与其相应的发生面与基锥的切线投影夹角

3.2 齿轮大端面齿顶圆和齿根圆方程

大端齿顶圆方程为：

式中：

δa--顶锥角，即矢径与Z轴的夹角σ--矢径在XOY平面的投影与X轴的夹角大端齿根圆方程为：

式中：δf--根锥角，矢径与Z轴的夹角

σ--矢径在XOY平面的投影与X轴的夹角

然后，我们可以根据式（3-2）和式（3-3）两式在CATIA环境中运用公式和函数命令创建点，然后用样条线连接各点可以得到弧齿锥齿轮大端面的齿槽轮廓。

3.3 齿轮小端面齿廓方程

图1 螺旋角示意图

节线上任意一点的螺旋角的计算公式为：

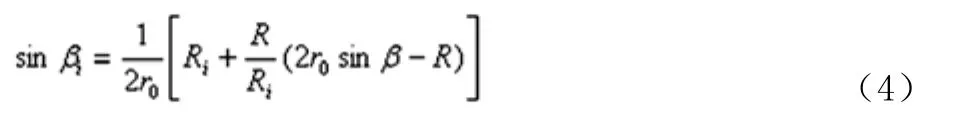
式中r0为刀盘半径。

3.4 弧齿锥齿轮齿形线方程

齿顶锥的齿形线方程：

式中，R为矢径

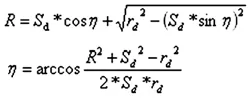
η--偏角

δa--齿顶角

δf--齿根角

λ--矢径在XOY平面的投影与X轴的夹角

然后根据上述方程编辑公式，再通过CATIA的law命令建立弧齿锥齿轮渐开线与齿形线的关键点，最后利用GSD模块（创成式外形设计）里面的样条线（spline）命令将关键点进行连接，进而可以得出齿形曲线轮廓，再分别于大小端面齿顶、齿根圆处倒圆角和修剪，即可得到轮齿齿槽曲线。

4 基于CATIA的参数化实体建模

4.1 输入弧齿锥齿轮各参数

在CATIA 中输入弧齿锥齿轮参数值和公式如下表2所示（以从动大齿轮为例）：

表2 弧齿锥齿轮参数表

4.2 创建基本曲线

4.2.1 创建齿轮定位草图

进入CATIA的GSD模块，绘制弧齿锥齿轮的定位草图，来作为轮齿大、小端面的草图定位，尺寸约束引用已经输入的参数值，如图2所示：

图2 定位草图

b.创建齿轮大、小端面基本圆

在(a)步绘制的定位草图基础上创建大、小端所在平面，大端面基本圆尺寸约束的参数化公式由内到外为：

“df/cos(delta)/2”、“db/cos(delta)/2”、“d/cos (del ta)/2”、“da/cos(delta)/2”,

小端面基本圆尺寸约束的参数化公式由内到外为：

“(df-2*bf*sin(delta_f))/cos(delta)/2”、“(db-2*bb*sin(delta_b))/cos(delta)/2”、“(d-2*b*sin(delta))/cos(delta)/2”、“(da-2*ba*sin(delta_a))/cos(delta) /2”。

最终生成弧齿锥齿轮大、小端面基本圆草图，如图 3所示：

图3a 齿轮大端面基本圆草图

图3b 齿轮小端面基本圆草图

c. 创建弧齿锥齿轮球面渐开线曲线

单击“公式”，输入大、小端面基本圆公式“r1=db/cos(delta)/2”、“r2=(db-2*bb*sin(delta_b))/cos(delta)/2”，单击“规则”图标，定义大端渐开线曲线方程x1，y1，

即：

“x1=r1*cos(PI/2*t)+r1*PI/2*t*sin(PI/2*t)”、“y1=r1*sin(PI/2*t)-r1*PI/2*t*cos(PI/2*t)”。

同理，定义小端渐开线曲线方程x2、y2，

即：

“x1=r2*cos(PI/2*t)+r2*PI/2*t*sin(PI/2*t)”、“y2=r2*sin(PI/2*t)+r2*PI/2*t*cos(PI/2*t)”

得弧齿锥齿轮大、小端面渐开线如图4所示（红色圆圈内部分）：

图4 弧齿锥齿轮齿轮大、小端渐开线曲线图

最后，镜像大小端齿轮渐开线曲线并修剪和接合所得曲线，得到大小端齿槽的轮廓曲线如图5所示：

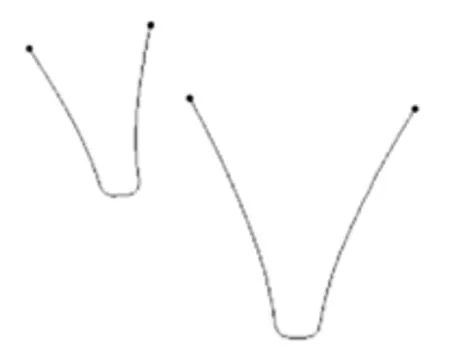
图5 弧齿锥齿轮大、小齿端齿槽齿廓曲线图

d.创建齿形间轮廓曲面

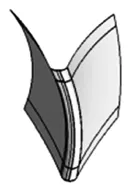
图6 齿轮齿槽曲面图

4.3 创建弧齿锥齿轮原始毛坯

进入CATIA“零件设计”绘制旋转体草图如图7所示：

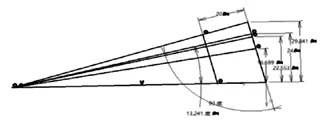
图7 毛坯旋转体草图

以上步中的毛坯草图为旋转轮廓，以定位草图斜边为旋转轴，单击确定，结果如图8所示：

图8 弧齿锥齿轮毛坯实体图

4.4 最终模型的生成

图9 齿槽轮廓曲面阵列后的模型

阵列齿槽曲面得到如图9所示的模型。

用阵列后的齿槽曲面对实体分割得到如图所示的齿轮模型。

图10 完成建模后的弧齿锥齿轮零件模型

同理可以得到参数化的主动弧齿锥齿轮模型如图 11所示：

图11 完成建模后的主动弧齿锥齿轮零件模型

5 结语

本文对汽车单级主减速器中的重要零件——主、从动弧齿锥齿轮参数化建模方法进行了研究。通过对弧齿锥齿轮的参数化建模，得到的参数化的弧齿锥齿轮模型可以通过修改参数而得到新的齿轮模型，极大的缩短了设计周期，对工程实际应用具有重要的意义。

参考文献

[1] 肖生发.汽车构造[M].北京:北京大学出版社,2012.

[2] 张云杰,刘鹏,乔建军.CATIA V5中文版入门与提高[M].北京:清华大学出版社,2012.

[3] 闻邦椿.机械设计手册[M].北京:机械工业出版社,2010.

[4] 邓效忠.魏冰阳.锥齿轮设计的新方法[M].北京:科学出版社,2012.

[5] 王裕清,武良臣.弧度锥齿轮接触区理论与切削过程分析[M].北京:煤炭工业出版社,2004.6.

[6] 朱孝录,等.齿轮传动设计手册「M].北京:化学工业出版社,2004.