一种优化网络生存时间的移动传感节点覆盖调度算法

杨海波，陈友荣，刘半藤，祝云凯，苏子漪

（1.浙江树人大学信息科技学院，浙江 杭州 310015；2.浙江杭佳科技发展有限公司，浙江 杭州 310015）

1 引言

在无线传感网（wireless sensor network，WSN）中，节点的能量约束限制了网络覆盖、生存时间等基本功能。网络高覆盖能确保从传感节点收集的数据准确表示监控区域。根据感知对象的不同，网络覆盖可分成目标覆盖、栅栏覆盖和区域覆盖。其中，目标覆盖要求传感节点能覆盖到所有目标点。当目标点遍布于监测区域且数量足够多时，目标覆盖问题可转换成区域覆盖问题。栅栏覆盖要求传感节点能完整覆盖一条直线。当直线数量足够多时，栅栏覆盖问题也可转换成区域覆盖。区域覆盖问题是网络覆盖的基本问题之一，可应用到环境监测、智慧工厂、入侵检测等多个领域[1-3]。同时，网络生存时间是指WSN从整个网络收集数据的有效工作时间。网络生存时间越大，则WSN的寿命越长，其应用成本越短，因此在环境监测等应用领域，WSN的设计应保持令人满意的区域覆盖和持续几个月或几年时间收集所需的感测数据（如温度），并传输给基站[4,5]。

目前许多研究侧重于同构无线传感网（所有传感节点具有相同的性能，如安装有相同的传感器、其位置都静止或都可以移动）的网络覆盖问题，如参考文献[6]考虑每一个传感节点的数据感知具有方向性，建立和采用列生成法求解生存时间优化模型。参考文献[7]建立和求解最小工作传感节点个数和最大网络覆盖的优化模型，确定每一个传感节点的工作调度。参考文献[8]将监测区域分成多个网格，每一个网格的传感节点选择成为簇头和成员，并采用一种权值计算式和提出传感节点的移动选择算法。参考文献[9]提出最大每一个移动传感节点的覆盖率和最大所有移动传感节点覆盖率的多目标优化模型，并求解该优化模型获得最优解。总之，参考文献[6,7]考虑传感节点的位置固定不变。参考文献[8,9]考虑所有传感节点都可移动。而且参考文献[6-9]考虑同构传感节点，但是在一些特殊应用中，传感节点存在感知范围、能量等方面的异构。

随着无线传感网应用领域的不断扩大，同构无线传感网已经不能满足实际应用的需要，如在无线传感网的典型应用——环境监测中，需要监测大气温度、湿度、光照强度等环境信息。显然每个传感节点不可能同时安装所有传感器，需要考虑安装有不同类型的传感器，即感知半径不同的异构传感节点。因此一些学者研究异构传感节点的覆盖问题，如参考文献[10]提出一种基于多重覆盖算法的异构节点调度算法。该算法建立覆盖率最大和工作节点数量最小的多目标优化模型，采用差分进化算法求解获得最优方案。参考文献[11]将覆盖问题转换成多个直线的覆盖问题，并建立直线覆盖的传感节点移动优化模型。采用线性求解算法求解获得最短移动路径。但是参考文献[10,11]是集中式方法，其计算量随着传感节点个数的增加而急剧增大。参考文献[12]根据邻居覆盖集合的信息，提出传感节点的调度，从而最小覆盖监测区域且保证网络连接。参考文献[13]根据邻居节点的不同位置，采用冗余方法对自身节点进行判断。如果判断冗余，则关闭冗余节点。虽然参考文献[12,13]是分布式方法，但是这些算法都没有考虑网络生存时间，也没有考虑当枢纽传感节点失效时覆盖盲区的修复问题。同时参考文献[10-13]只是考虑异构静态传感节点的调度，没有考虑异构传感节点的移动性，容易出现能量空穴问题，因此部分学者考虑异构传感节点的移动，研究异构移动传感节点的覆盖问题，如参考文献[14]根据传感节点的数量，判断每一个网格的负载，负载高的网格中部分传感节点向负载低的网格移动。参考文献[15]在位置进化中考虑异构传感节点间的虚拟力，提出虚拟力导向差分算法，从而优化覆盖率。参考文献[16]考虑监控区域内存在覆盖盲点，提出一种能耗最小和感知覆盖最大的覆盖洞修补算法，获得异构传感节点的移动规划路径。但是参考文献[14-16]都是集中式算法，其算法计算量较大，一般只适合传感节点数量较少的网络，而且只是考虑所有传感节点具有移动性，需要配置移动设备和大功率的电池，大大增加了无线传感网部署的成本。

综上所述，目前同构静态或移动传感节点的覆盖优化算法没有考虑传感节点的异构性。异构静态传感节点的覆盖优化算法同样存在能量空穴问题。异构移动传感节点的覆盖优化算法主要偏向于假设所有传感节点具有移动性，具有较大的硬件成本，且侧重于集中式方法，较少涉及分布式算法。因此在上述参考文献的基础上，为降低系统的硬件成本，考虑环境监测等应用中同时存在异构静态传感节点和少量移动传感节点。当网络启动后，静态传感节点的分布不均匀造成覆盖盲区，或者当网络运行一段时间后，部分静态传感节点因能量耗尽而死亡，造成网络覆盖盲区时，利用传感节点的移动，提出一种优化网络生存时间的移动传感节点覆盖调度算法（coverage scheduling algorithm，CSA）。在CSA中，静态传感节点根据邻居静态传感节点的信息，发现静态传感节点的覆盖盲区和估计移动传感节点的停留位置，广播通知移动传感节点。同时建立移动传感节点的移动优化模型，分布式求解该优化模型，获得异构移动传感节点的分布式移动策略，修补覆盖盲区，从而保证最大网络覆盖，尽可能提高网络生存时间和降低算法的时间复杂度。

2 网络模型和算法设计

在CSA中作出如下假设。

（1）在二维的无线传感网中，同时存在静态传感节点、移动传感节点和静态sink节点。移动传感节点可移动到监控区域的任一位置。

（2）传感节点的感知覆盖异构，即每一个传感节点的感知覆盖半径不一致。

（3）传感节点通过 GPS、北斗等卫星定位模块或其他定位算法，获知自身的位置坐标。

（4）静态传感节点可处于工作状态或者睡眠状态。处于工作状态的传感节点定时感知数据，并将数据发送给sink节点。

（5）传感节点具有相同的通信半径和初始能量，且采用如下数据发送和接收能耗计算式计算自身能耗。

其中，Efa表示节点数据发送能耗，Ejie表示节点数据接收能耗，Dataij表示传感节点i需要发送给邻居传感节点j的数据量，Eelec表示数据处理能耗参数，εfs表示数据发送能耗参数，dij表示传感节点i到邻居传感节点j的距离。

传感节点随机分布在监测区域内且需要获知自身的位置，如图1所示。每一个传感节点具有不同的感知半径。当网络运行后，静态传感节点分析周围邻居传感节点的位置和剩余能量状态，判断是否存在覆盖盲区。采用少量的移动传感节点修补覆盖盲区，从而提高感知覆盖和网络生存时间。但是CSA仍需要解决以下3个问题：静态传感节点如何根据邻居传感节点的位置、剩余能量等信息，判断其周围是否存在覆盖盲区，并估计移动传感节点的停留位置；如何根据停留位置，建立移动传感节点的覆盖调度模型；如何分布式求解覆盖调度模型，从而移动传感节点可移动到合适位置，修补覆盖盲区，提高网络生存时间。这3个问题的具体解决如下。

2.1 停留位置计算

当网络运行后，主要存在两种覆盖盲区的生成情况。一种是传感节点的能量耗尽，则其负责的覆盖区域出现覆盖盲区，此时直接将该传感节点的位置作为移动传感节点的停留位置。另一种是由于传感节点位置分布的随机性，传感节点部署后出现覆盖盲区，此时采用如下方法确定移动传感节点的可选停留位置。

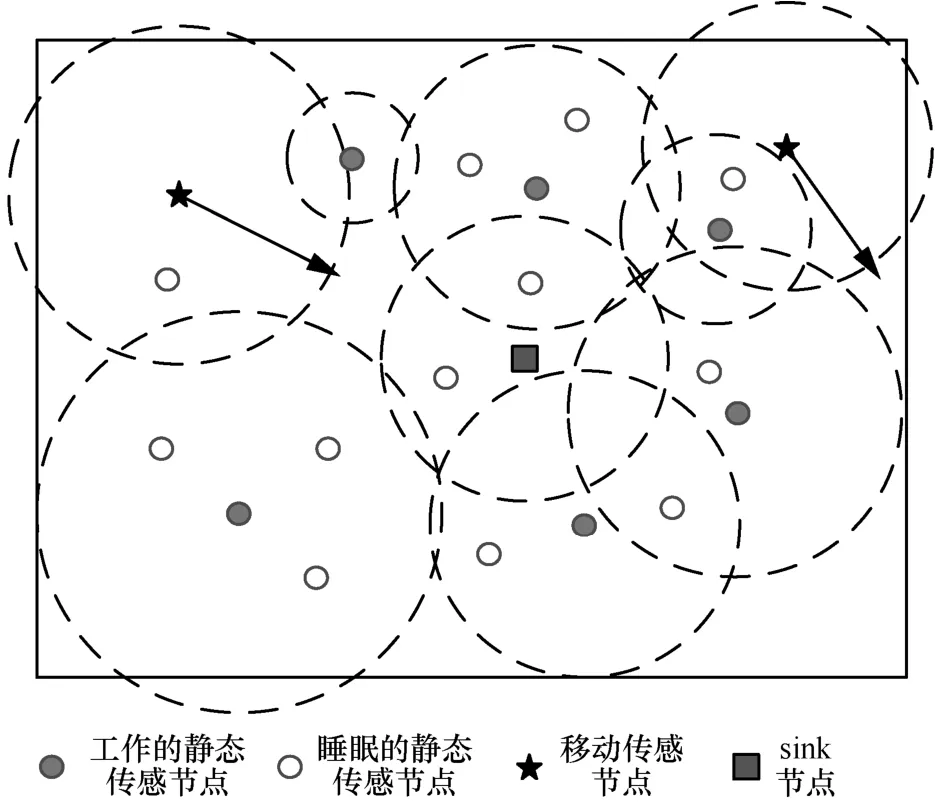
图1 CSA原理

当传感节点部署后，通过与邻居传感节点通信，获知邻居传感节点的位置、感知半径等信息，如图2所示。根据自身感知半径，在自身感知圆弧上确定间隔相同的Nhu个点位置，其中Nhu表示圆弧上计算点个数，选择感知半径相交的邻居传感节点位置，并计算Nhu个点是否被邻居传感节点覆盖。即：

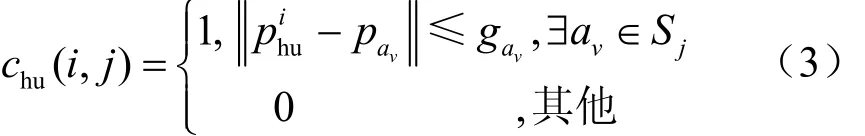
其中，chu(i,j)表示与自身节点j的圆弧上第i个点是否被邻居传感节点覆盖的标识符。表示覆盖，否则表示不覆盖。表示圆弧上第i个点的位置，表示邻居传感节点av的位置坐标，表示邻居传感节点av的感知半径，Sj表示与自身节点j的感知半径相交的邻居传感节点集合，表示两位置的距离。根据Nhu个点的状态，合并所有标识符为0的相邻位置，可获得多个未覆盖的弧及其两端点位置。

如果静态传感节点存在未覆盖的弧，其两端顶点为A和B，坐标分别为和则图2中C点的坐标满足以下计算式：

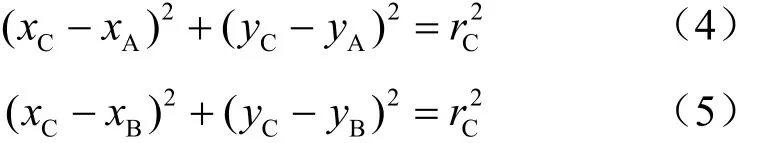
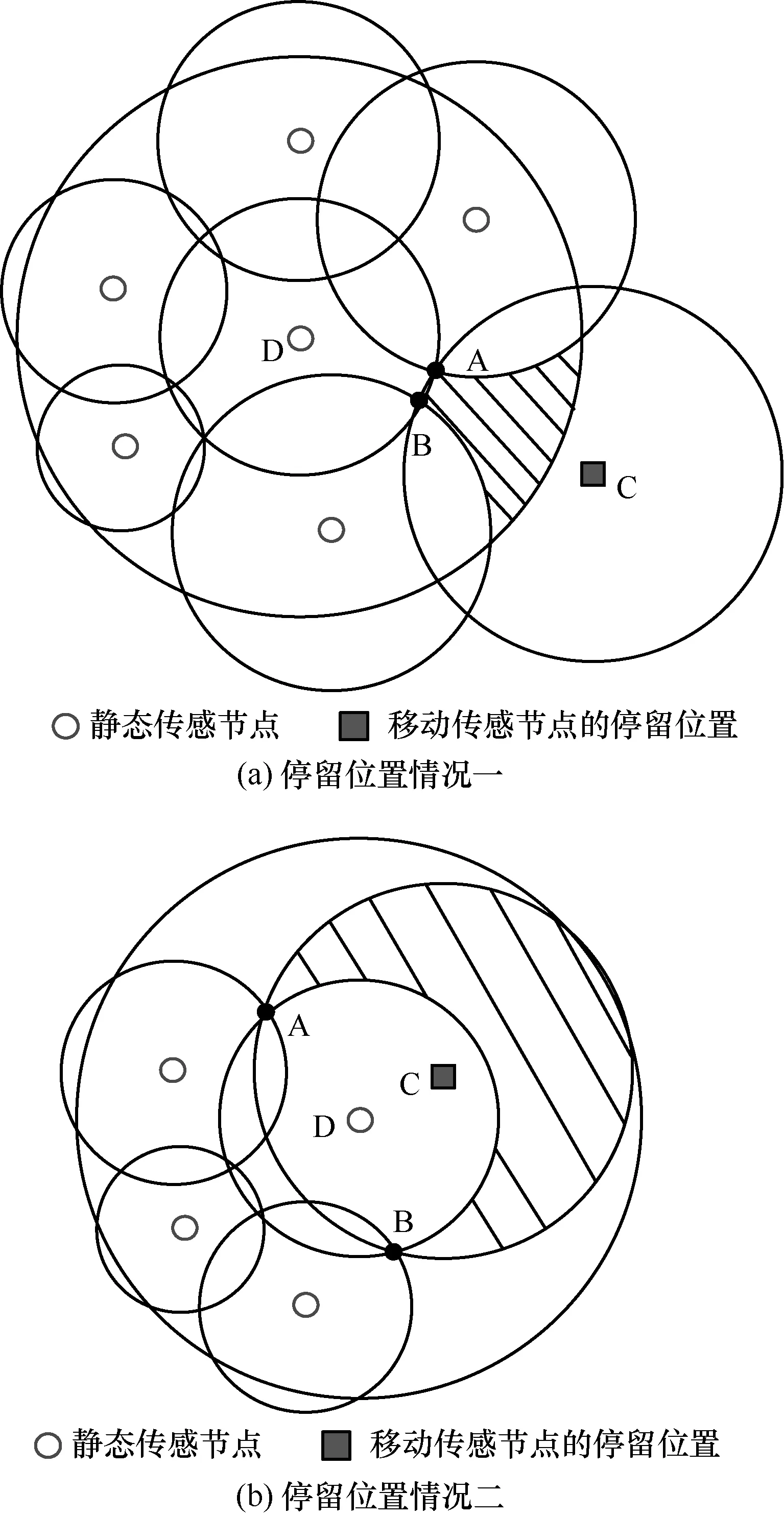
图2 静态传感节点的移动传感节点停留位置选择

其中，rC表示圆C的半径。式（4）减式（5），可得：

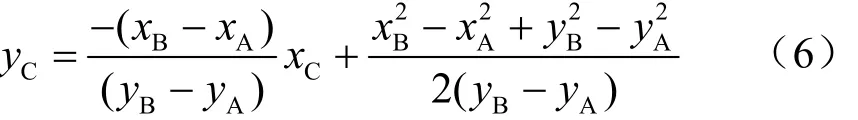
将式（6）代入式（4），并令，求解得：

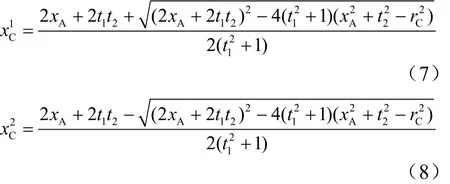
根据式（6）可得和，即C点的两种可能性和 (根据两点可选坐标，分别计算到自身圆点D的距离且

当自身节点未覆盖弧的角度0 ≤θL≤ π ，则选择作为自身节点期望的移动传感节点位置，否则选择作为自身节点期望的移动传感节点位置。如果存在多个不连续的未覆盖弧，则分别计算这些弧所对应的移动传感节点位置，即可估计移动传感节点的位置。

2.2 覆盖调度模型建立

当覆盖盲区不能被静态传感节点覆盖时，此时需要移动传感节点移动修复该区域。令当前移动传感节点的数量为Nm，移动传感节点的初始位置为pm=(xm,ym)，新的停留位置则移动传感节点新的位置区域覆盖率增量Δc overp为：

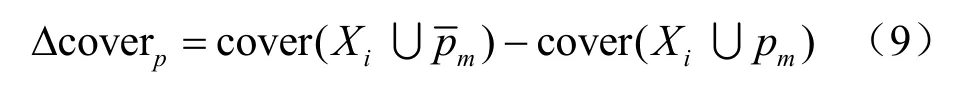
其中，Xi表示负责计算停留位置的传感节点i和其处于工作状态邻居传感节点的位置集合，表示根据Xi中传感节点位置的区域覆盖率。为方便计算覆盖率，如图 3所示，以传感节点i的自身位置为中心，将周围区域分解成多个网格。如果该区域网格中心在处于工作状态的传感节点的感知覆盖区域内，则该网格被覆盖，即：

其中，cgv(Xi)表示集合Xi下网格gv是否被覆盖的标识符，则区域覆盖率的计算式为：

其中，ngrid表示网格的个数。

移动传感节点从初始位置移动到新位置的路程为：

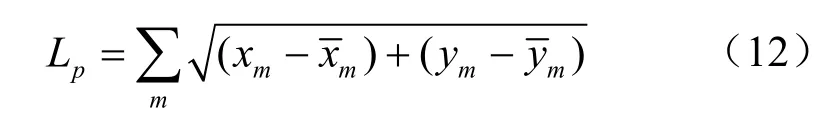
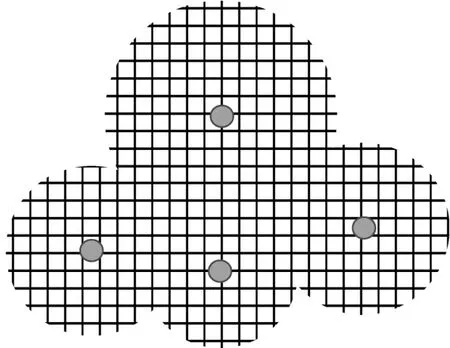
图3 传感节点的覆盖计算方法

需要让所有移动传感节点新的位置区域覆盖率增长最多且移动路程最短，则获得如下目标函数：

根据上述的多目标问题，建立以下优化模型：

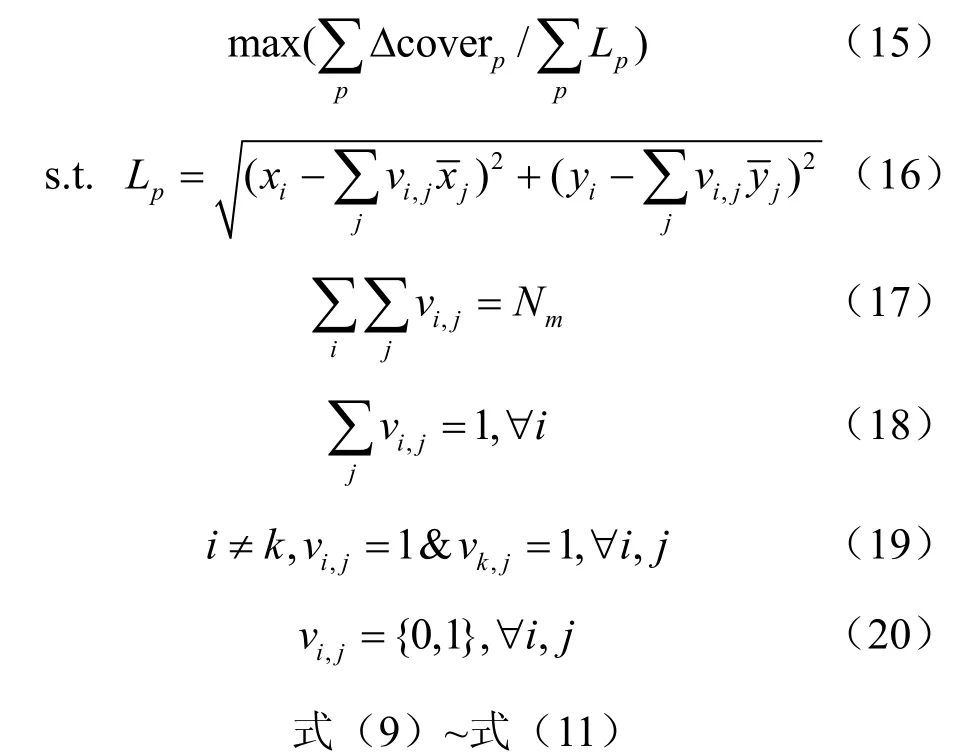
其中，vi,j表示一个移动传感节点i是否移动到该集合中位置j的标识符。当时，该节点将移动并停留在该位置上，否则不移动。式（16）表示移动传感节点从当前位置移动到新位置的路程，式（17）表示当前移动传感节点的数量为Nm，式（18）表示同一个移动传感节点只能移动到某一个固定位置，式（19）表示不同的移动传感节点不能移动到同一个位置，则移动传感节点的覆盖调度问题转化成匹配问题。

2.3 算法设计

覆盖调度模型——式（15）可采用遗传算法、粒子群算法等人工智能算法求解该优化模型，但是上述算法是集中式算法，需要能收集所有传感节点的算法处理中心，且计算量较大，因此采用包括静态传感节点和移动传感节点的启发式方法求解该优化模型，获得较优方案，具体 CSA设计如下。

设第i类生产设备的第k台机器在一个工作日内用于生产第j种零件的时间为xikj(k=1,2,…,pi)．类似地，对每一台设备，被分配用于生产所有零件的工作时间总和为1，即有约束条件:

在CSA中，静态传感节点、移动传感节点和sink节点分别执行各自不同的算法。sink节点定时发送盲区计算分组和路由信息分组，并通过多跳传输收集所有传感节点的感知数据。静态传感节点完成程序初始化后，监听不同的分组，并判断属于不同的情况，执行不同的程序，是一个事情驱动的算法。如图4所示，具体实现步骤如下。

步骤 1 网络启动后，设置定时时间。定时时间到后发送包含自身位置、感知半径、剩余能量等状态信息的节点信息分组。

步骤 2 接收所有邻居传感节点的位置、感知半径、剩余能量等状态信息，存储到邻居传感节点的状态信息表中。

步骤3 如果接收sink节点的盲区计算分组，则根据所有邻居静态传感节点的位置，判断其弧是否全覆盖，如果其弧未全覆盖，计算未覆盖弧中连续子弧的数量NL和每一个子弧的两个端点位置坐标，根据式（7）、式（8）计算移动传感节点位置的两种可能，根据子弧的角度确定每一个子弧所对应的移动传感节点位置。计算需要移动传感节点停留的可选位置坐标和位置权重，向未盲区计算的邻居传感节点转发盲区计算分组。

步骤 4 如果接收到邻居传感节点的能量失效分组，获知该邻居传感节点的位置、感知半径等信息。计算需要移动传感节点停留的位置坐标和位置权重。

步骤 5 如果存在到移动传感节点的路径且需要发送停留位置，则将包含有停留位置、权值等信息的移动传感节点请求分组多跳传输给移动传感节点。

步骤 6 如果接收到移动传感节点的路由查询分组，则记录到该移动传感节点的路径。判断路由查询分组的跳数。当完成m跳后，则不转发该分组，否则转发该分组。

步骤 7 如果接收到移动传感节点的位置确认分组或位置取消分组，则广播通知其周围的其他静态传感节点。

步骤 8 如果接收到静态传感节点的位置确认分组，则考虑该位置停留移动传感节点。如果接收到静态传感节点的位置取消分组，则考虑该位置没有停留移动传感节点，重新判断其弧是否全覆盖。如果其弧未全覆盖，更新移动传感节点位置和其权值。

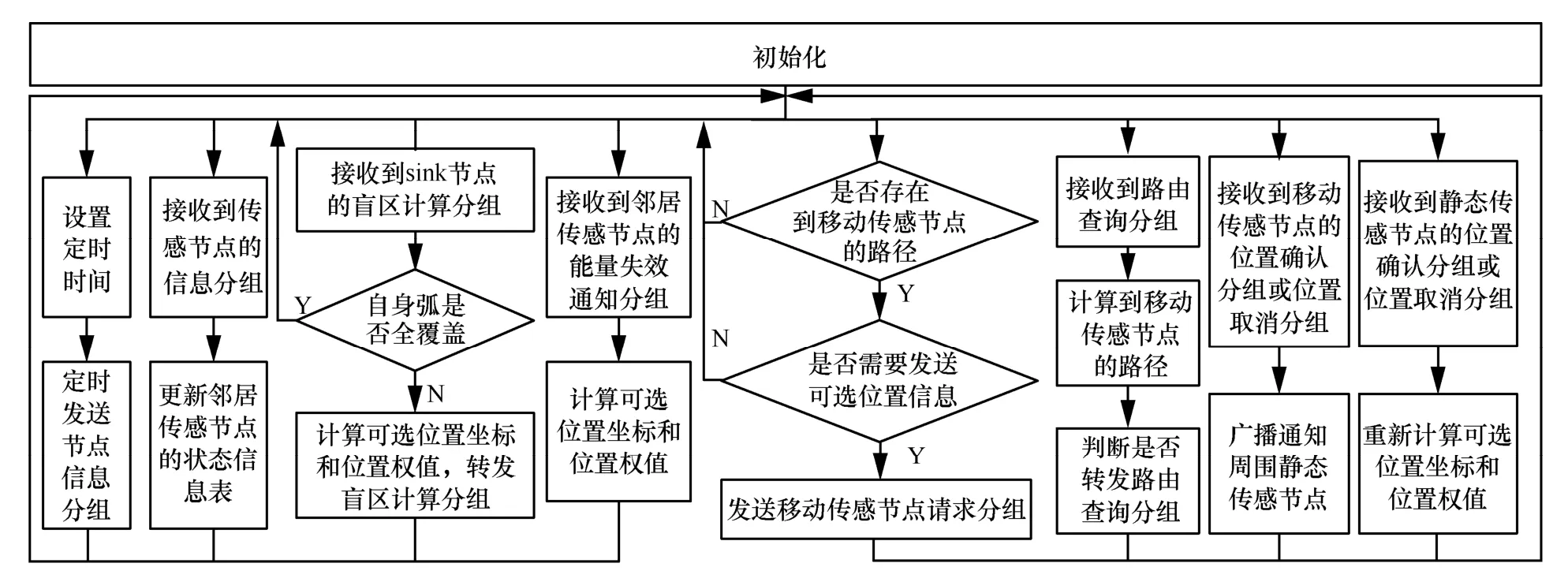
图4 CSA的静态传感节点的工作流程

网络启动后，移动传感节点根据静态传感节点的位置信息分组，选择并移动到目标位置。如图5所示，具体实现步骤如下。

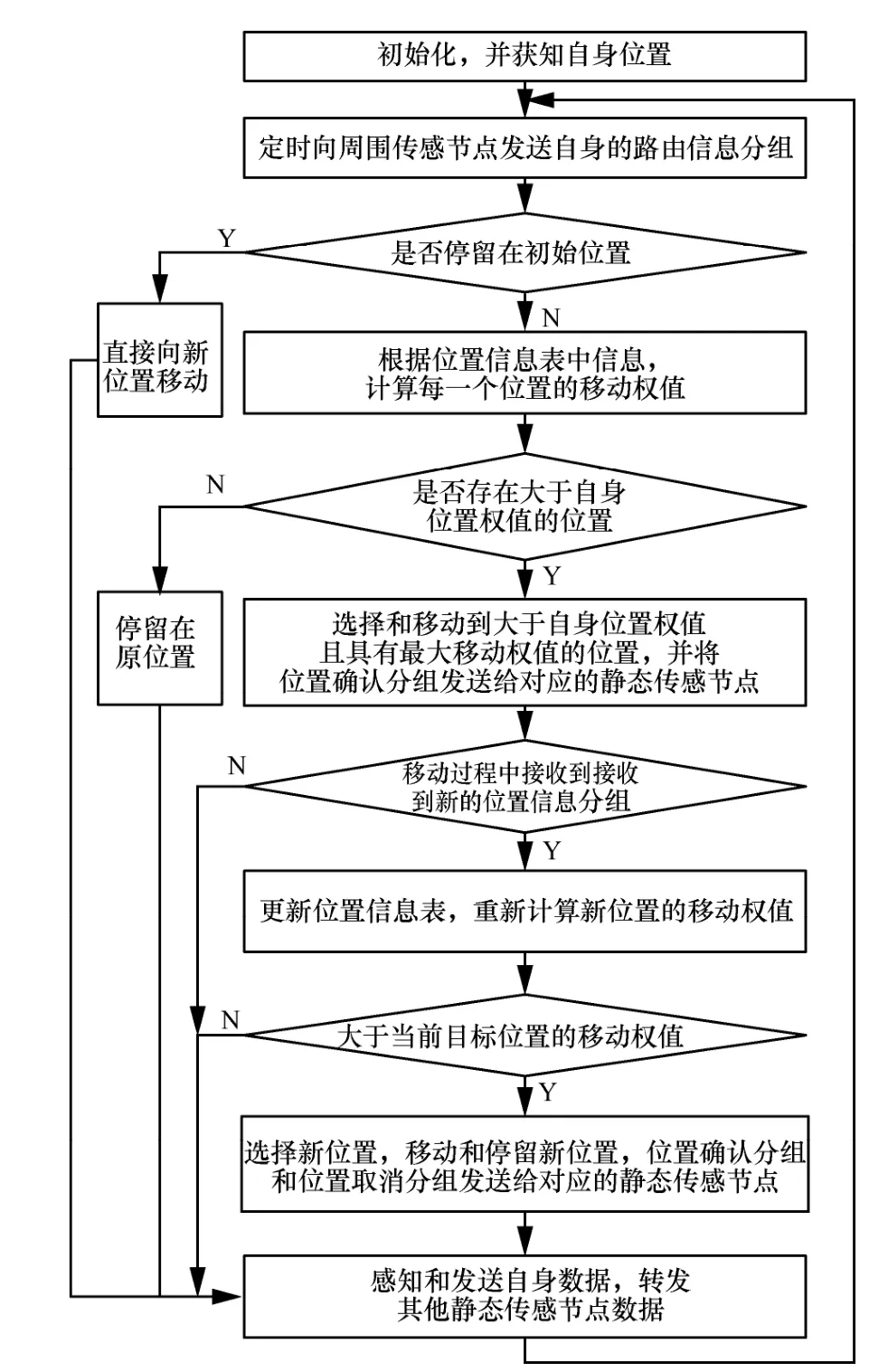
图5 CSA的移动传感节点的工作流程

步骤1 初始化，并获知自身位置。

步骤2 定时向周围传感节点发送自身的路由信息分组。

步骤 3 如果接收到传感节点的停留位置坐标和位置权重，则将该分组信息添加到可选位置信息表中。

步骤4 如果停留在初始位置，则直接向该位置移动，跳到步骤5，否则根据位置信息表中的信息，计算每一个位置的移动权值并比较自身位置的位置权值。如果存在大于自身位置权值且具有最大移动权值的位置，选择和移动到该位置，并将位置确认分组发送给对应的静态传感节点，否则仍停留在原位置。如果在移动过程中接收到新的位置信息分组，则更新位置信息表，重新计算新位置的移动权值其中Li′表示已经移动的距离，表示当前最新位置到可选位置信息表中的距离。如果大于当前目标位置的移动权值，则选择新位置作为移动目标位置，将位置确认分组和位置取消分组发送给对应的静态传感节点。

步骤 5 移动和停留在当前目标位置，感知和发送自身数据，转发其他静态传感节点数据。

如图4和图5所示，CSA算法是一个分布式算法，其时间复杂度分析主要是分析静态传感节点和移动传感节点的时间复杂度。静态传感节点主要是根据每一个邻居传感节点的信息，计算可选位置坐标和位置权重，即其时间复杂度为，其中ni表示传感节点i的邻居传感节点个数。移动传感节点主要是根据接收到的静态传感节点停留位置信息分组，选择和移动到目标位置，即其时间复杂度为，其中np表示移动传感节点接收到的期待停留位置个数，因此CSA算法对时间复杂度的要求不高。在消息交互过程中，由于静态传感节点的状态信息和路由查询、移动传感节点路由信息等信息可整合到路由算法的消息分组中，且位置确认分组、位置取消分组、能量失效分组等消息分组是根据发生的事件选择发送，因此CSA的消息开销不大。

3 算法仿真

3.1 仿真参数选择和比较算法

在仿真中，只考虑无线传感网感知数据的无线通信能耗，不考虑信息分组传输能耗、数据计算能耗等其他能耗。根据上述算法分析，采用MATLAB R2014a软件，编写M语言程序仿真实现不考虑移动传感节点算法（Mno）、MNode[8]、MGrid[14]和CSA 4种算法，并比较各算法性能参数。其中，MNode算法让移动传感节点选择最近的失效节点位置作为其停留位置。MGrid算法将监控区域划分成多个大小相同的网格，让移动传感节点选择存在覆盖盲区的网格中心停留。即在仿真实验中随机均匀产生[50 m, 150 m]区间的静态传感节点感知半径，随机均匀产生监控区域内传感节点的位置分布，选择分布式贪婪算法（disturbed greedy algorithm，DGA）[8]调度静态传感节点的工作状态，选择分布式Bellman_Ford算法[17]作为传感节点的数据路由算法，考虑移动传感节点可移动修复覆盖盲区，并采用以下参数实现算法仿真，输出网络生存时间、区域覆盖率、存活静态传感节点个数、平均静态传感节点能耗等性能参数值：监测区域的长和宽均为1 000 m，传感节点的最大通信半径为200 m，移动传感节点的感知半径为 200 m，传感节点个数为100，一次数据收集周期的传感节点感知数据量为1 Mbit，初始能量Einital为1 000 J，数据处理能耗参数Eelec为50 nJ/bit，数据发送能耗参数εfs为100 pJ/(bit·m2)，圆弧上点个数Nhu为 50。其中定义一个数据收集周期（data collection period，DCP）表示 sink节点收集完监控区域内处于工作状态的所有传感节点1 Mbit数据所需要的时间。x%区域覆盖的网络生存时间定义为网络启动后，传感节点保持x%以上区域覆盖的DCP个数。区域覆盖率定义为处于工作状态的静态传感节点和移动传感节点覆盖面积和监控区域面积的比值。存活静态传感节点个数定义为网络启动到当前时间，处于工作和睡眠状态的静态传感节点个数。平均静态传感节点能耗定义为静态传感节点的总能耗与静态传感节点个数和 DCP个数的比值。

3.2 仿真结果分析

采用第 3.1节的仿真参数和移动传感节点个数20，分别计算Mno、MNode、MGrid和CSA 4种算法的区域覆盖率和存活静态传感节点个数，获得图6和图7。

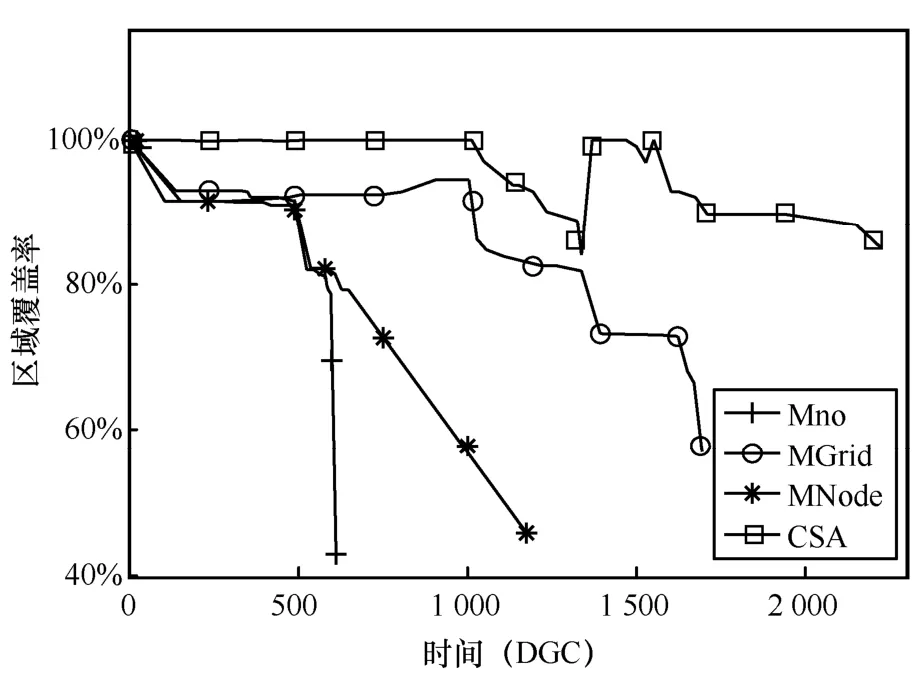
图6 区域覆盖率的变化曲线

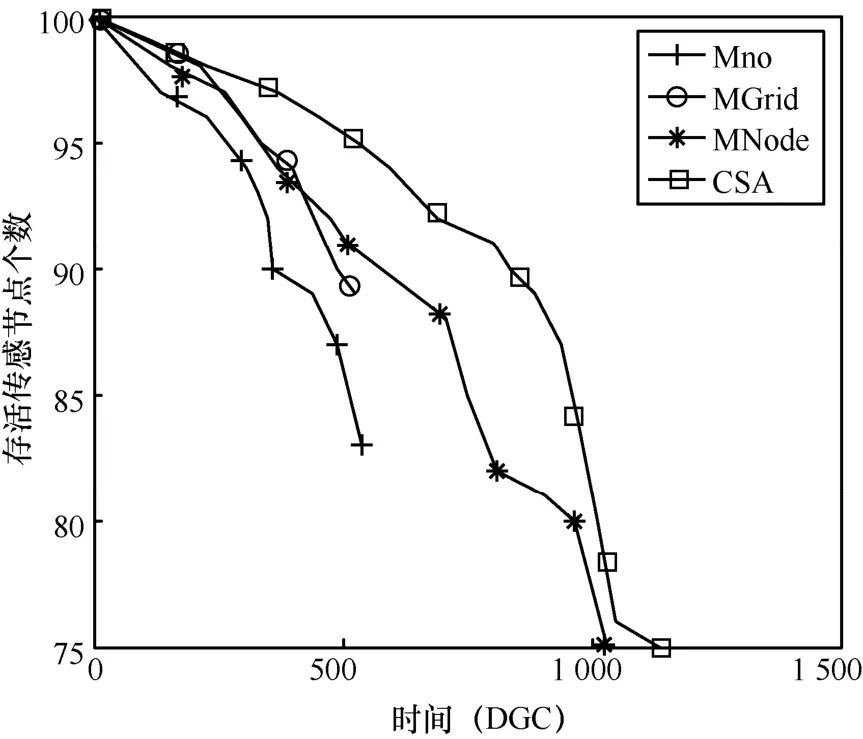
图7 存活静态传感节点个数的变化曲线

CSA保持相同区域覆盖率的 DCP个数高于Mno、MNode和MGrid算法，如图6所示。这是因为在移动传感节点的调度中，CSA让移动传感节点停留在失效节点的位置，修复因节点失效引起的覆盖盲区，让移动传感节点停留在静态传感节点计算的可选位置，修复因节点位置分布出现的覆盖盲区，尽可能让移动传感节点停留在合适的位置，同时在保证最大化覆盖的情况下提高网络生存时间。Mno算法没有考虑移动传感节点，没有移动传感节点的修复功能，因此相同区域覆盖率的DCP个数最低。MGrid算法只是选择网格中心的位置，可选位置有限，MNode算法选择失效节点的位置，只是考虑覆盖盲区出现的一个方面。因此，Mno、MNode和MGrid算法的网络生存时间比CSA算法的网络生存时间低。而且由于移动传感节点移动覆盖的效果较好，当覆盖率第一次下降时，通过移动修复，其网络覆盖率重新达到100%。因此其覆盖率曲线是上下起伏。

随着 DCP个数的增加，静态传感节点因能量耗尽而死亡，因此各个算法的存活静态传感节点个数随之下降，如图7所示。但是除了一小段时间，MNode的存活静态传感节点个数高于其他3个算法，在大多数时间内，CSA算法因移动传感节点停留在适合的位置，调度静态传感节点工作，其平均节点能耗较少，存活的传感节点个数大于Mno、MNode、MGrid算法。

最后，选择移动传感节点个数5、10、15、20、25、30，随机产生10个均匀分布的拓扑结构。在仿真过程中，由于静态传感节点随机分布，静态传感节点的初始位置没有覆盖整个监控区域，Mno、MNode、MGrid算法只考虑到局部信息，较难覆盖整个监控区域。虽然CSA能修复传感节点分布的覆盖盲区，但是很难与上述3个算法比较。因此计算Mno、MNode、MGrid、CSA算法的 90%区域覆盖的网络生存时间和平均节点能耗，取其平均值作为仿真结果值。

保持90%以上的区域覆盖下CSA的网络生存时间比Mno、MNode和MGrid算法的网络生存时间长，如图8所示。Mno算法没有考虑移动传感节点。在MNode算法中，移动传感节点选择距离最近的能量失效节点移动。在MGrid算法中，移动传感节点选择距离最近且具有覆盖盲区的网格中心位置移动。这3个算法只是考虑覆盖的某一个方面，而CSA同时考虑能量失效节点和传感节点分布所引起的覆盖盲区，让移动传感节点选择合适的停留位置停留，从而其网络生存时间略高于Mno、MNode和MGrid算法。

图8 90%区域覆盖的网络生存时间比较

图9 90%区域覆盖的平均静态传感节点能耗比较

如图9所示，Mno算法只考虑静态传感节点工作，其平均静态传感节点能耗较高，MGrid算法的移动传感节点停留位置不够理想，网络生存时间相对较短，其平均静态传感节点能耗较高。MNode和 CSA算法的平均静态传感节点能耗较低。当移动传感节点个数为20、25和30时，网络中移动传感节点数量较多，CSA充分利用移动传感节点修复两种覆盖盲区，网络生存时间较高，其平均静态传感节点能耗小于MNode算法。因此90%区域覆盖下，CSA的平均静态传感节点能耗小于Mno、MNode和MGrid算法的平均静态传感节点能耗。

4 结束语

本文提出了一种优化网络生存时间的移动传感节点覆盖调度算法（CSA）。首先，提出算法假设。提出移动传感节点覆盖调度的基本原理，具体包括停留位置的估计、覆盖调度模型建立和启发式求解方法。其次，提出CSA的实现，包括sink节点、移动传感节点和静态传感节点的实现步骤。最后给出算法的仿真参数，采用分布式Bellman_Ford算法实现数据路由，采用DGA算法实现静态传感节点的覆盖调度，仿真比较Mno、MNode、MGrid算法和CSA的性能。

总之，相比 Mno、MNode和 MGrid算法，CSA提高了区域覆盖率和静态传感节点存活个数。不管移动传感节点个数如何变化，在保持相同的区域覆盖率下，CSA提高了网络生存时间和降低了平均静态传感节点能耗。但是CSA只是选择启发式算法求解覆盖调度模型，其移动传感节点的位置选择只是当前移动方案的较优解，因此下一个阶段目标是采用分布式最优化方法求解覆盖调度模型，获得移动传感节点的停留位置选择最优方案。

参考文献：

[1]卓琨, 张衡阳, 郑博, 等.无人机自组网研究进展综述[J].电信科学, 2015, 31(4)： 134-144.ZHUO K, ZHANG H Y, ZHENG B, et al.Progress of UAV Ad Hoc network： a survey[J].Telecommunications Science, 2015,31(4)： 134-144.

[2]魏颖琪, 林玮平, 李颖.物联网智能终端技术研究[J].电信科学, 2015, 31(8)： 146-152.WEI Y Q, LIN W P, LI Y.Study on key technologies of intelligent IoT device[J].Telecommunications Science, 2015, 31(8)：146-152

[3]肖清旺, 王锦华, 朱易翔.物联网智能终端设备识别方法[J].电信科学, 2017, 33(2)： 3-8.XIAO Q W, WANG J H, ZHU Y X.Intelligent terminal device identification method of internet of things[J].Telecommunications Science, 2017, 33(2)： 3-8.

[4]CASTILLO I D, TOBAJAS F, ESPER CHAIN R, et al.Hardware platform for wide-area vehicular sensor networks with mobile nodes[J].Vehicular Communications, 2016, 3(1)： 21-30.

[5]冯剑, 王平阳, 王琳, 等.基于能量获取的无线通信系统研究[J].电信科学, 2015, 31(2)： 124-131.FENG J, WANG P Y, WANG L, et al.Research on energy harvesting communication system[J].Telecommunications Science, 2015, 31(2)： 124-131.

[6]SINGH A, ROSSI A.A genetic algorithm based exact approach for lifetime maximization of directional sensor networks[J].Ad Hoc Networks, 2013, 11(3)： 1006-1021.

[7]IDREES A K, DESCHINKEL K, SALOMON M, et al.Distributed lifetime coverage optimization protocol in wireless sensor networks[J].The Journal of Supercomputing, 2015, 71(12)：4578-4593.

[8]AHMED M K, WALID O.Mobility-assisted minimum connected cover in a wireless sensor network[J].Journal of Parallel and Distributed Computing, 2012, 72(7)： 827-837.

[9]BARA A A, ENAN A K, SUAT O, et al.A multi-objective disjoint set covers for reliable lifetime maximization of wireless sensor networks[J].Wireless Personal Communications, 2015,81(2)： 819-838.

[10]李明.基于差分算法的异构无线传感器网络多重覆盖节点调度方案[J].传感技术学报, 2012, 25(6)： 826-830.LI M.A weighted multiple coverage node scheduling scheme based on differential evolution algorithm for heterogeneous sensor networks[J].Chinese Journal of Sensors and Actuators,2012, 25(6)： 826-830.

[11]杜晓玉, 孙力娟, 郭剑, 等.异构无线传感器网络覆盖优化算法[J].电子与信息学报, 2014, 36(3)： 696-702.DU X Y, SUN L J, GUO J, et al.Coverage optimization algorithm for heterogeneous WSN[J].Journal of Electronics & Information Technology, 2014, 36(3)： 696-702.

[12]KHEDR A M, OSAMY W.Minimum connected cover of a query region in heterogeneous wireless sensor networks[J].Information Sciences, 2013, 223(2)： 153-163.

[13]孙力娟, 魏静, 郭剑, 等.面向异构无线传感器网络的节点调度算法[J].电子学报, 2014, 42(10)： 1907-1912.SUN L J, WEI J, GUO J, et al.Node scheduling algorithm for heterogeneous wireless sensor networks[J].Acta Electronica Sinica, 2014, 42(10)： 1907-1912.

[14]NUDURUPATIA D P, SINGHA R K.Enhancing coverage ratio using mobility in heterogeneous wireless sensor network[C]//International Conference on Computational Intelligence： Modeling Techniques and Applications (CIMTA), Sept 27, 2013, Kalyani, India.Piscataway： IEEE Press, 2013：538-545.

[15]李明, 石为人.虚拟力导向差分算法的异构移动传感网络覆盖策略[J].仪器仪表学报, 2011, 32(5)： 1143-1150.LI M, SHI W R.Virtual force-directed differential evolution algorithm based coverage-enhancing algorithm for heterogeneous mobile sensor networks[J].Chinese Journal of Scientific Instrument, 2011, 32(5)： 1143-1150.

[16]刘军, 程良伦, 王建华, 等.一种混合异构传感网的覆盖洞修补算法[J].控制与决策, 2015, 30(11)： 2080-2084.LIU J, CHENG L L, WANG J H, et al.A coverage hole repair algorithm for hybrid heterogeneous sensor networks[J].Control and Decision, 2015, 30(11)： 2080-2084.

[17]陈友荣, 王章权, 程菊花, 等.基于最短路径树的优化生存时间路由算法[J].传感技术学报, 2012, 25(3)： 406-412.CHEN Y R, WANG Z Q, CHENG J H, et al.Lifetime optimized routing algorithm based on shortest path tree[J].Chinese Journal of Sensors and Actuators, 2012, 25(3)： 406-412.