基于用户移动网络接入位置的高效分布式相似矩阵计算方法

王源，江昊，吴明，姚冬桂，张毅，羿舒文，汪海，吴静

（1.武汉大学电子信息学院，湖北 武汉 430072；2.武汉船舶通信研究所，湖北 武汉 430070；3.武汉技师学院，湖北 武汉 430051）

1 引言

近年来，大数据的处理和运用在各行各业逐渐占据重要位置，从大数据中获取的海量信息为人们提供着生活体验的全方位改善。随着数据量的不断增大，数据处理过程对软硬件的需求也随之增加，人们越来越迫切地需要找到能够适应大规模数据的高效处理方式。

在实际的大数据处理中，对不同的数据来源有不同的处理方式，而在众多的数据来源中，用户移动网络接入数据是一种具有代表性的包含多维属性的数据，其最主要的意义之一就是用于对用户的兴趣和习惯进行分析和挖掘。利用用户移动网络接入数据，可以构建用户网络图，根据获得的用户网络图可以进行社区发现[1]。在网络中，如果两个节点间相连，就认为它们相似——这就是社区发现[2]，连边的权重则区分了用户与用户间不同的相似程度。随着社交网络规模的逐渐扩大，人与人之间的联系日益密切，在这些大的网络中寻找相似点间的社区和子集变成了资源密集型作业[3]。由于社区发现基于用户之间相似度实现，过程中必然涉及相似矩阵计算，例如余弦相似度的计算中使用的矩阵乘法需要大量的 I/O开销和内存开销，为整个计算流程带来了极大的时间复杂度。

传统矩阵乘法的时间复杂度是O(n3)，1969年Strassen[4]利用分治算法，将时间复杂度降至O(n2.8074)，Strassen算法的这一优化在现实实践中得到了广泛的应用。这些算法现在已经被封装成成熟的程序包，比如 Jampack[5]和 JAMA[6]。在此基础上，近年来也有不少学者在不断地尝试创新和优化，Duc等人[7]提出了一种基于 Strassen算法的并行化实现，能够在一定程度上减少运行时间，但是却增大了递归深度。Scripps等人[1]提出了一种基于Jaccard因子的社区发现并行算法，取得了良好的效果。然而，由于矩阵乘法本身的计算复杂性，通过对矩阵乘法过程优化获得运算效率提升的难度不断增大，如果能够结合应用场景和数据特征对矩阵乘法的计算复杂度进行一定的优化，则能够在特定的场景下获得更好的效果。

一方面，在实际的应用场景（如习惯发现、协同过滤、兴趣推荐）中进行社区发现时会有大量无关用户之间的连边，这些连边在社区发现过程中将被剔除，但却会在相似矩阵计算过程中给系统带来不必要的资源消耗；另一方面，用户移动网络接入数据在实际使用中会根据场景需要进行筛选，只留下与研究目标关联性较强的信息，忽略其他信息，而这些被忽略的信息也许能够以先验知识的形式为后期工作提供便捷。

针对以上问题，本文将对基于用户移动网络接入数据进行社区发现过程中的相似矩阵计算方法进行优化，提出一种基于用户移动网络接入位置的分布式相似矩阵计算方法，利用先验地理位置信息对用户进行划分，只对相近用户进行相似度计算以减少数据冗余，从而实现更高效的相似矩阵计算方法，并与现有算法进行效率和效果比对，证明其在实际应用中有更为出色的性能。

2 多种场景下的矩阵运算相关研究

矩阵运算在数据挖掘领域有着广泛的应用，如图像处理、文本挖掘[8]、推荐系统和生物信息学等[9]。不同的应用领域和应用场景对矩阵的运算需求有所不同，其优化方向和方式也大相径庭。

在推荐系统、用户兴趣和习惯发现领域，矩阵运算普遍应用于根据用户属性矩阵挖掘用户的相似度，其中包括皮尔逊相似度、余弦相似度在内的相似度度量方法均涉及矩阵乘法。在图像处理领域，图像本身就是由像素组成的矩阵，在去噪、模糊图像处理等过程中更无可避免地使用到矩阵乘法等。在图像处理、文本挖掘等领域，已有许多研究工作者尝试将新的技术应用到矩阵乘法中，以提升其在各自领域的效率。Reza等人[10]将输入矩阵分割并将它们存储在独立的数据节点并触发各节点上的CUDA核，以提升整体计算效率。Malysiak 等人[11]提出了一种在多个装有GPU的节点上进行分布式矩阵乘法的方法。Giza-Belciug等人[12]针对本体映射的相似矩阵乘法提出了一种并行优化算法。然而，在用户兴趣和习惯发现领域，却尚未提出有针对性的矩阵乘法计算策略优化方案。

与此同时，随着数据量的增大，单节点的硬件资源已无法高效地满足数据处理需求，大量分布式解决方案也被提出，其中最有代表性的就是Apache的开源项目Hadoop。Hadoop在数据挖掘领域有着广泛的应用价值，包括用户聚类和社区发现领域，Zhang等人[13]、Mann等人[14]和Shahrivari等人[15]都尝试将 Hadoop应用于K-means算法中，Lu 等人[16]和Song等人[17]则将Hadoop应用于KNN（K-nearest neighbor）算法中。针对目前高维数据矩阵乘法中所存在的问题，孙远帅等人[9]介绍了两种利用Hadoop进行并行矩阵乘法计算的方法：一种是内积法；另一种是外积法。内积法充分利用了MapReduce的并行性，但同时也大大增加了 Shuffle传输的中间数据量[9]。外积法比内积法的 MapReduce 实现少了很多中间数据，但损失了并行粒度[9]。针对上述问题，笔者提出了一种新的分块计算方法，能够通过调整子块的维度实现较好的性能表现。

上述解决方案较原始的矩阵处理方法而言都有一定的性能提升，在各个领域也都有不错的表现，但都着眼于改进矩阵乘法的过程以提升其性能，而均未考虑到应用中数据本身的特殊性及其所包含的信息。如在用户兴趣和习惯发现领域，计算用户相似矩阵时，如果对所有数据进行计算，所消耗的资源会随着用户量或特征维度的增加不断增加。而事实上，用户行为数据中包含大量时间和空间信息，如果能够对这些信息加以适当的利用，就有可能为计算带来一定的帮助。

综上，在实际的应用中，不同应用场景对矩阵运算提出了不同的需求，如果可以根据不同的背景和需求进行有针对性的矩阵运算方法设计，将能够为其性能和效果带来更进一步的提升。

3 基于用户移动网络接入位置的相似矩阵计算方法

3.1 用户访问行为分析

用户行为中存在一定的长尾特性和指数分布特性，现有的许多工作都对这些特性进行了分析和证明[18-21]。在移动网络的访问过程中，用户的访问行为存在一定的随机性[22]，本文对用户访问的位置和内容进行了统计，统计出了用户访问过的内容数和位置数，具体如图1所示。

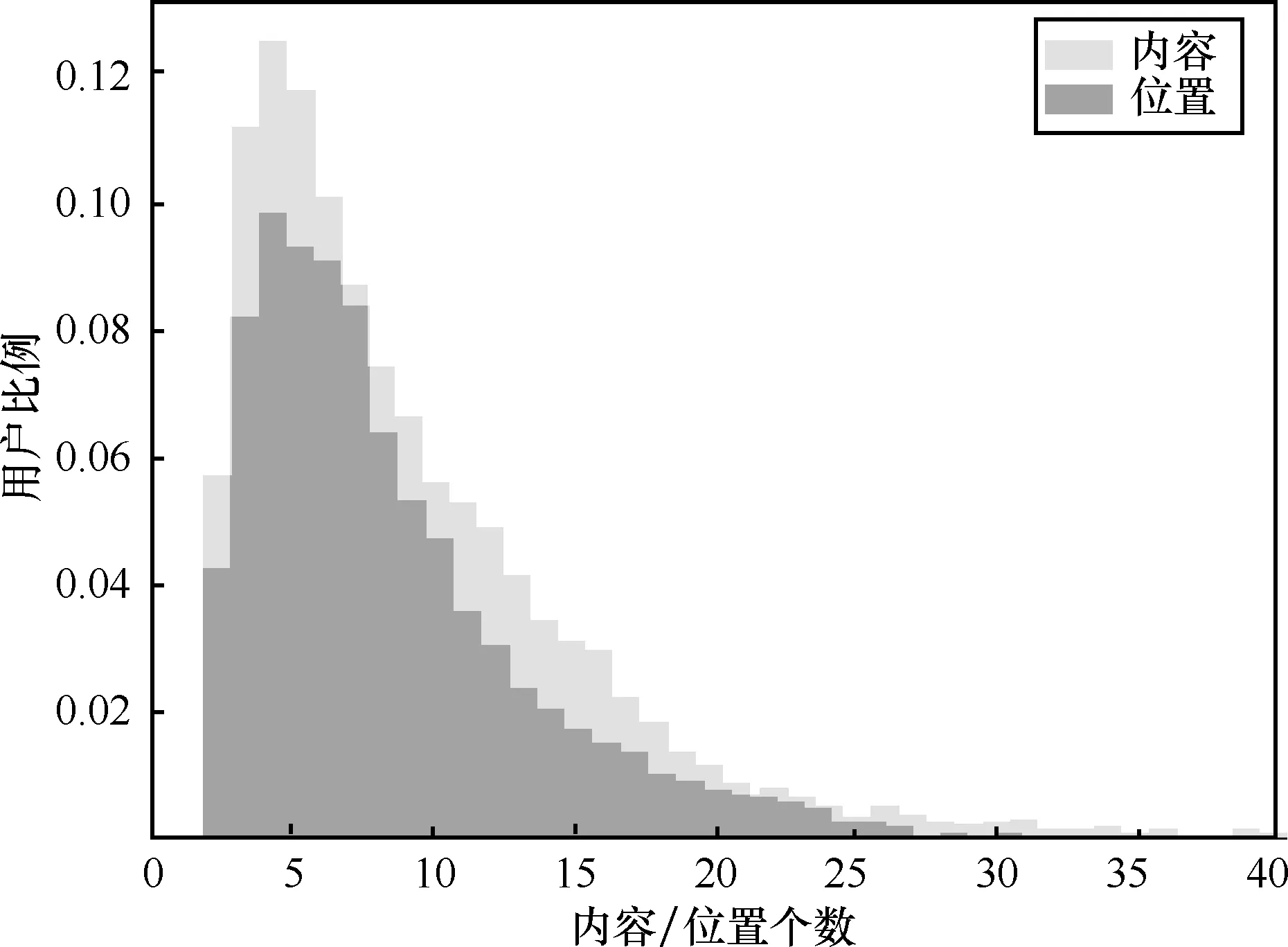
图1 用户访问的内容数和位置数统计

从图1中可以看出，大部分用户的访问内容和位置都在5个左右，且绝大部分用户访问的位置和内容都在10个以内。值得一提的是，用户访问的位置与内容相比具有更强的局限性。基于这种特性，可以认为用户在访问过程中位置相对固定，内容也相对固定，那么距离较远的用户产生关联的可能性也就越小，也就是相似度越小。

为了说明用户访问位置和用户访问内容之间的相关性，本文以用户间的 JS散度（Jensen-Shannon divergence）作为用户访问行为相似程度的度量，JS散度定义如式（1）所示：

其中，JS(⋅)对于所有PA、PB有JS( ⋅)∈ ( 0,1)，KL(⋅)表示KL散度（Kullback-Leibler divergence），其定义如式（2）所示：

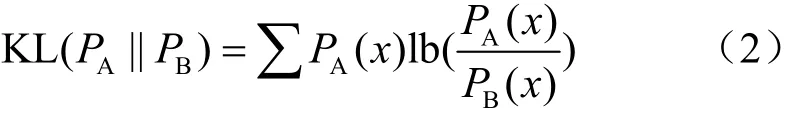
其中，PA、PB分别为用户A和用户B的访问内容分布。本文定义，且有 JS D∈ ( 0,1 0 0)，计算了两两用户间的内容分布JSD值，并绘制所有用户中的JSD值分布和使用本文用户划分方法划分后的一个用户分块中的JSD值分布，具体如图2所示。

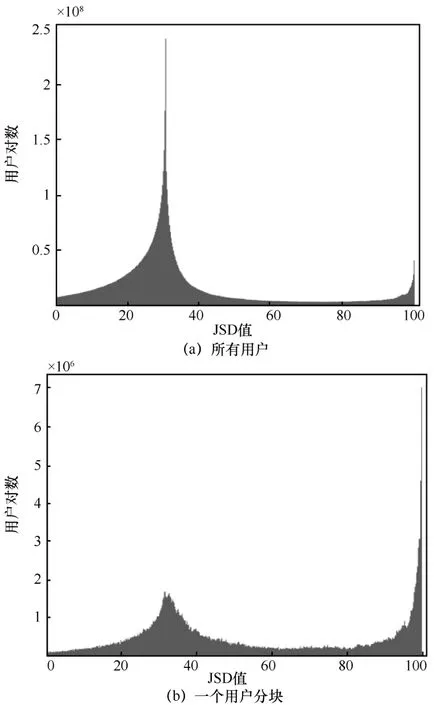
图2 用户间JSD值分布

由图2中可以看出，图2（a）中的峰值出现在JSD值为30左右时，而图2（b）中的峰值出现在JSD值为100时，根据JSD的定义可知，越大的JSD值意味着越强的相似度，显然，图2（b）中的用户相较于图2（a）中的用户展现出更强的相似性，故经过划分后的用户块中的用户在访问的内容分布上有更强的相似性，而从全局的角度来看，大部分用户之间的访问内容分布相似度较低。

在社区发现的过程中，相似度过低的用户之间的连边属于无效连边，即这条连边的存在与否对最终结果几乎没有影响，反而会降低运算效率。于是，本文基于用户访问位置相对固定的特性，根据用户的位置对用户进行预先划分，并依据划分结果对相邻的用户进行相似度的计算，以提升计算效率。

3.2 方法架构

为提升相似矩阵的计算效率，同时有效利用系统中的计算资源，本文基于分布式计算框架对相似网络计算方法进行了设计，其架构如图3所示。

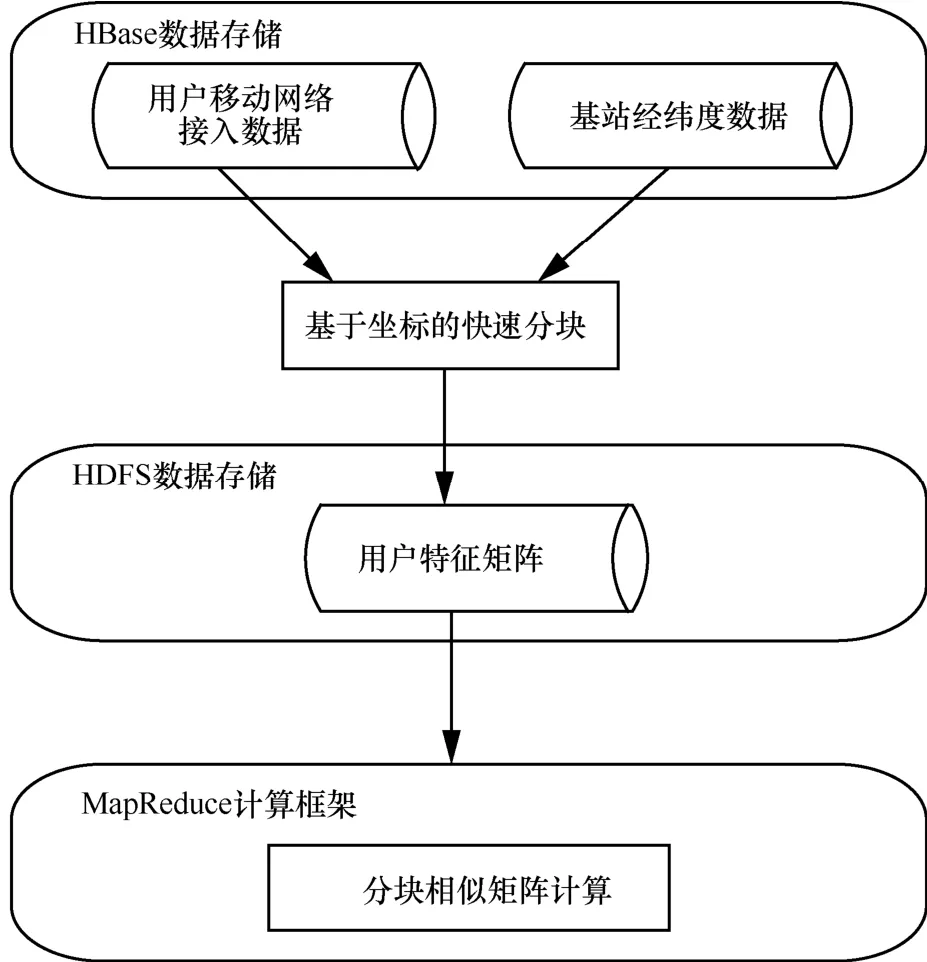
图3 基于用户移动网络接入位置的相似矩阵计算方法架构

整个架构和工作流程分为4个部分，分别是HBase数据存储、基于坐标的快速分块、HDFS数据存储和MapReduce计算框架。HBase中存储原始用户移动网络接入数据和基站经纬度数据。原始用户移动网络接入数据以用户的每一条移动网络接入记录为数据库中的一行，列包括用户ID、记录开始时间、记录结束时间，所访问基站的LACID和cellID、所访问基站的坐标以及所访问的内容URL。其中，所访问基站的坐标由基站的经纬度换算得来。基站经纬度数据则以每一个基站为一行，列包括基站的LACID和cellID、基站的经纬度信息，开始计算之前将会根据基站经纬度数据计算出基站的直角坐标。

基于坐标的快速分块策略是根据计算得到的基站直角坐标对基站进行块划分，具体划分方法见第3.3.1节，划分后得到基站分块，然后根据用户对不同块中基站的访问时长，将用户划分至访问时长最长的块中，得到用户分块。

HDFS上存储的是基于坐标的快速分块策略得到的用户分块结果文件，存储形式为三元组，即用（x,y,n）来表示第x行第y列的值为n。为了提升存储和传输效率，HDFS只存储矩阵中不为0的元素，对于稀疏矩阵而言，能够大大减少存储所需的空间和传输带宽。

计算时首先进行数据预处理，将基站的经纬度信息转换成直角坐标。接着对格式化的用户访问矩阵进行基于坐标的快速分块，即先将基站根据坐标分块，然后依此对用户进行分块。分块后得到的用户特征矩阵以三元组的形式存储在 HDFS上。最后根据划分结果进行基于MapReduce的用户相似矩阵计算，得到最终的相似度矩阵。

3.3 关键技术

3.3.1 基于坐标的快速分块策略

基于坐标的快速分块策略基本步骤如图4所示。首先根据基站的位置将基站划分入不同的网格中，如图4（a）所示，其中圆点表示基站，具体先根据基站所属行政区面积及所需的分块大小决定分块个数，并确定基站集合：{b1,b2,…,bn}，然后根据坐标值的范围结合所需分块个数确定划分节点，根据划分节点对基站直角坐标进行截取或转换，生成其所在块编号，具有相同编号的基站属于同一块，否则属于不同块。而属于不同块的基站编号之间的差值即可反映两基站所属块的邻近关系，不同的差值表示不同的方位上的距离。例如本文中基站直角坐标范围为（9 700 172.203 65，8 738 234.211 33）到（9 806 113.083 42，8 884 126.448 06），所需划分块个数为600个，故将坐标截短为（9 700, 9 806）到（8 738, 8 884），对x、y坐标以5为间隔划分，若x＜9 705，则x被划分到9 700，若9 705≤x＜9 710，则x被划分到9 705，以此类推，同样地，若y＜8 743，则y被划分为8 738，若8 743≤y＜8 748，则y被划分为 8 743，以此类推，则总共可划分的块数为。最后将x和y的划分结果合并生成基站的块编号，如基站（9 705,8 738），则其块编号为97058738，至此，所有基站拥有其块编号，块编号本身同时表征着基站之间的位置关系，得到划分块集合：{c1,c2,…,cm}。

接着根据用户对不同基站的访问时长，将用户划分至访问总时长最多的块，如图4（b）所示，其中圆点表示基站，它们分别属于不同的块，用户与基站的连线表示用户对基站的访问，连线的粗细程度表示用户在该基站的访问总时长，连线越粗表明用户对该基站的总访问时长越长。本文对用户的移动数据接入记录数据进行汇总整理，生成用户访问矩阵，在本文提出的相似矩阵计算方法中，强调用户的位置序列，故生成用户访问矩阵时对同一用户不同时段的访问情况进行无序叠加，得到用户xi访问基站时长的序列为{t1,t2,…,tk}，其中tj表示用户访问第j个基站的总时长，基站划分完毕后，根据用户所访问基站所在的块，计算每个块中的访问时长，并据此将用户定位到访问时长最长的块中。假设基站b1,b2,b3,b4,b5∈ci，那么用户xj对块ci的访问总时长则为：Ti=t1+t2+t3+t4+t5，依次获得用户对所有m个块的访问集合{T1,T2,…,Tm}，从中找出时长最长的块c，即用户所处的块。如图4（b）所示，用户访问次数最多的块是阴影部分，故将该用户划分到阴影块。

图4 基于坐标的快速分块策略基本步骤

最终生成用户的块划分结果如图4（c）所示，将用户定位到各个块中后，计算时只计算用户与其所在块及其周边8个块内用户之间的相似度。

3.3.2 分块相似矩阵计算方法

本文使用MapReduce框架作为相似矩阵计算的实现框架，其流程为：在map阶段将矩阵数据进行整理，根据规则将所需计算的用户及其周边8个块内的用户数据输入同一个reduce中，而在reduce中则对这些用户两两计算相似度，并输出最后的结果，算法伪代码如下。

输入：划分后用户完整访问矩阵，用户分块信息。

在map阶段输入划分后的用户完整访问矩阵和分块信息，首先处理分块信息，将分块信息作为静态变量，保存在一个HashMap数据结构中，其中将块的编号 BlockNum作为HashMap中的键，其对应的值为该块中的所有用户UserNum，然后处理用户访问矩阵，矩阵中的每一行即相似矩阵计算时的特征向量，其中还包含了该用户所在的块和该用户的编号。由于每一个用户需要和他所在块周围的8个块中的所有用户计算相似度，所以为了在 reduce阶段能够让需要计算相似度的用户特征向量分到同一个reducer中，每一个用户的特征向量会为所有需要与其计算相似度的用户输出一次。例如用户x有n个需要计算相似度的用户，那么对于用户x的map阶段将会产生n个输出，每一个输出的key为用户x的编号加上需要与x计算相似度的用户的编号组成的复合键，value则为用户x的访问向量。

由于map在处理不同的用户访问记录时，输出key值的顺序是不同的，例如，假设用户x和y之间需要计算相似度，那么在处理用户x的访问记录时，针对y的输出key值是（y，x），而在处理用户y的访问记录时，针对x的输出key 值是（x，y），故本文重新设计了 MapReduce中的key值比较算法，让map阶段key为（x，y）和（y，x）的输出能够被放入同一个reducer中。

在reduce阶段将完成对用户相似度的计算，其中每一个reducer处理的是两个用户的相似度计算。用HashMap暂存其中一个用户的特征向量，另一个用户则直接从HashMap中取相对应的值进行相似度计算即可。

3.3.3 高效存储及传输策略

本文中的数据存储策略分为原始数据存储和中间数据存储策略。原始数据存储策略将数据存储在分布式数据库HBase中，通过针对性的表存储结构设计实现数据的高效存取；中间数据存储则采用 Hadoop分布式文件系统（HDFS），通过设计文件中数据的存放方式及文件的备份机制，实现中间数据读写的低 I/O开销。

原始数据存储采用分布式数据库 HBase。HBase是Hadoop生态系统中的一个高可靠、高性能、列式存储、可伸缩的分布式数据库[23]。相较于传统数据库而言，HBase对于超大规模数据集有更为优良的存储表现和读写性能，特别是对于不强调数据间关系、对联合查询等没有需求的格式化数据存储有非常明显的优势。

用户移动网络接入数据是一种格式化数据，本文针对其特征设计存储格式，将数据存储到HBase中。存储方式见表1，为提升HBase性能，数据采用单列族存储方式，列族中列名即字段名称。值得一提的是，HBase数据表中的 RowKey（行键）设计，由于本文数据处理部分将对属于同一用户的网络接入数据进行合并处理，故RowKey以用户UID开头，后加上数据起始时间，以实现同一用户的数据存储在同一个RegionServer上，并按时间排序。

表1 HBase表存储方式

相较于传统文本数据输入方式而言，在数据处理时，直接从HBase中取出相应的字段输入而无需再次对数据进行分解，极大提升了程序效率。同时，使用本文的RowKey设计方式，可以有效地利用HBase的高效RowKey查询性能，提升程序运行过程中的数据访问效率。

考虑到MapReduce的适配性，中间数据存储采用 HDFS，将输出文件以 block的形式直接存放在HDFS的各个DataNode节点上，考虑到节点间数据传输的网络时延，结合DataNode节点的资源负载情况，将生成的中间数据以多副本形式存储，根据节点数量，对n个节点的集群将副本数设为n，在进行新一轮数据处理时，各DataNode节点可高效拉取本地备份的副本数据，降低网络开销，提升运行效率。

在实际应用中，用户的访问情况呈明显的聚集性，单个用户的访问范围有限，故在相似矩阵计算过程中产生的中间数据多为稀疏矩阵，针对此特性，本文将中间数据以三元组[24]的形式存储，将矩阵中的非零值以其行号和列号为标识存储，即以(x,y,n)表示第x行第y列的值为n，显然以这种存储方式存储稀疏矩阵可以极大地节省存储资源。

现有的基于MapReduce的分布式矩阵乘法算法中，基本采用两种map输出方式，一种为行（列）式输出，另一种则为点式输出。

在行（列）式输出方式中，对于矩阵P、Q：

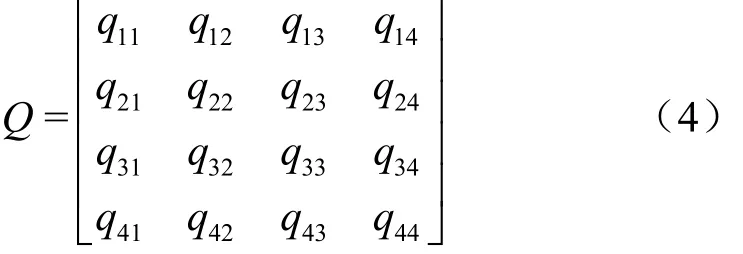
计算P×Q时将在map阶段对P、Q分别做如下划分：

将P的每一行和Q的每一列作为map的输出，在reduce中，则将行与列相乘得到结果矩阵中的对应元素。

而在点式输出方式中，则会对P、Q中的每一个元素进行划分，如下所示：

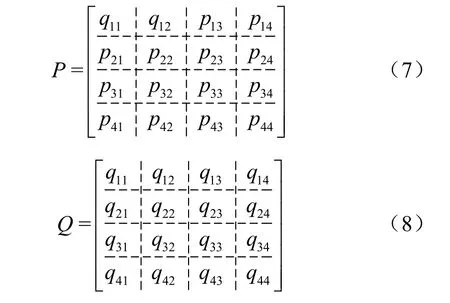
将P、Q中的每一个元素作为map的输出，而在reduce中依然将输出结果所对应的P中行的所有元素和Q中列的所有元素放到一起计算出最终结果，与行（列）式输出方式不同的是，点式输出方式在数据传输到reduce阶段时，已经包含了矩阵乘法中元素与元素间的对应关系，即已经知道p11与q11相乘、p12与q12相乘等，而无需再做判断。

点式输出的优势在于 reduce阶段的工作量小，因为在map输出数据中已经包含了其数据计算的对应关系，在reduce阶段只需根据这种关系进行计算即可；而行（列）式输出的优势则在于map的输出次数少，I/O开销小。在实际应用中，由于矩阵乘法并不涉及大量串行计算而只需简单的并行数乘，其主要开销集中于数据获取阶段和结果生成阶段的数据传输，数据传输时产生的I/O开销将会对效率产生更大的影响，故本文选用行（列）式输出以更好地提升其效率。

4 实验分析

4.1 数据集

本文采用浙江省金华市2014年11月21日—12月13日的用户UDR（usage detail record）数据作为原始数据集，为消除实验结果中的不确定因素和随机性，本文筛选了上网记录数较多的用户，分别是上网记录100条以上的70 099个用户、150条以上的49 031个用户、200条以上的20 846个用户、300条以上的18 479个用户、350条以上的14 566个用户、400条以上的11 827个用户和500条以上的3 468个用户。

用户接入数据和基站位置字段含义见表2，实验中使用uid作为用户的标识，lacID和cellID作为用户访问矩阵中不同基站的标识，同时根据数据流起止时间计算用户的上网时长，url为截短后的访问内容地址，以此区分用户对不同内容的访问次数。而在基站信息表格中，基站由 lacID和cellID唯一标识，根据基站所在位置经纬度换算成直角坐标，对基站进行分块。

表2 用户接入数据和基站位置字段含义

本文选取用户访问内容特征作为相似矩阵计算特征，从理论角度来看，内容特征与位置特征本身存在一定的联系，例如人们在家里经常访问娱乐相关的内容，而在办公区域则主要浏览工作相关的内容；同时，如图 2所示，有相同位置特征的用户在访问内容分布上也呈现出一定的规律性，例如，在同一间办公室的职员会互相分享有价值的内容，故这些职员的访问内容分布会呈现出相似性。从实际应用角度来看，内容特征反映了用户之间的兴趣维度，在用户的访问行为研究和应用中，该特征被广泛地应用于各种场景，如兴趣发现、推荐系统、D2D[25]、流量卸载、边缘缓存和计算[26]等，故对用户内容特征相似度计算的研究对实际的应用有极大的价值。

4.2 实验配置及流程

所有的实验均在由 4台服务器搭建的Hadoop集群上完成，其中一台服务器作为Hadoop集群的NameNode，装有64位CentOS 6.5操作系统，磁盘容量为1 TB，内存为48 GB，配有双核CPU6；另3台服务器作为Hadoop集群的DataNode，装有64位CentOS 7.0操作系统，磁盘容量为3.6 TB，内存为128 GB，配有双核CPU8。

实验中，本文所提出的算法将首先对用户进行划分，对于划分过的用户，只计算用户及其相邻块（包括自己所在的块）中用户之间的相似度。而对比实验中不对用户进行划分，计算所有用户两两间的相似度，相似矩阵计算过程则借用参考文献[9]中所提出方法的思想，实现方案在第 4.4节介绍。相似度矩阵计算完成后，将两种实验结果应用于Louvain社区发现算法，实验结果将在第4.6节介绍。

4.3 参数选择对效果的影响

经分析发现，移动网络用户的活动范围多在10 km左右，而其访问基站的个数也大多集中在5个左右，故选取10 km作为实验中块划分的距离。

考虑到分块的大小为 10 km，且计算时用户将与周边8个块内的用户计算相似度，实际的计算范围为 30 km，远大于用户的活动半径，本文采用以访问总时长最长的块作为用户所在的块的划分方式，可以在不影响计算准确性的前提下提升计算效率。

4.4 对比实验设计

为保证公平性，本文实验中的所有算法均使用MapReduce框架在分布式环境下实现。本文对比实验设计参考文献[9]中所提到的方法，由于本文介绍的基于地理位置的分布式相似矩阵计算方法采用行（列）式输出方式，故对比实验采用第3.3.3节介绍的点式输出方式，同时在70 099个用户的实验中，由于用户数据量过大，故采用分块矩阵乘法以遵循对比实验所采用方案的设计思想，达到对比效果。

4.5 性能指标

本文以用户访问矩阵作为输入，用户相似矩阵作为输出，以从输入到输出的程序运行时长作为实验的效率对比标准。在一致性方面，将两种计算方法生成的相似矩阵输入 Louvain社区发现算法，对比两种社区发现结果，定义未将用户进行分块的社区发现结果为划分前社区发现结果，用户分块后的社区发现结果为划分后社区发现结果。将划分前社区发现结果中，在同一社区内的两位用户之间的连边作为社区内边数记录，而将划分后社区发现结果中的社区内连边和划分前社区发现结果中的社区内连边的交集作为“好边”记录，以“好边”相连的用户则作为正确用户记录，若无“好边”与之相连则为错误用户。

4.6 实验结果分析

实验分别对两种方法的性能和结果一致性进行了对比。如图 5所示为不同用户数划分前后相似矩阵计算耗时，显然，划分前的计算耗时随着用户数的增加呈指数形式增长，而划分后的计算耗时随着用户数的增加呈线性增长。例如在3 468个用户的实验中，未划分时相似矩阵计算耗时106 s，划分后相似矩阵计算耗时42 s；在20 846个用户的实验中，未划分时相似矩阵计算耗时约30 min，划分后用时约8 min；在70 099个用户的实验中，未划分时相似矩阵计算耗时约360 min，划分后用时约14 min，两者相差达25倍之多。不妨以方阵为例对这个现象进行分析，普通矩阵乘法的复杂度为O(n3)，而对于进行了划分之后的相似矩阵计算，假设划分为m个块，每个块和周围8块之间计算相似度，那么计算复杂度为，令，那么复杂度可化简为，其中k≥1，由于m可以随着n值变化而调整，令k为常量，故划分后的相似矩阵计算耗时关于n呈线性增长。值得一提的是，在70 099个用户的相似矩阵计算过程中加入了矩阵分块处理步骤，而实验表明，在如此大规模的矩阵计算中，即使进行了矩阵分块，由于分块带来的巨大传输需求对分布式集群的资源消耗巨大，导致最终的计算成本依然居高不下。显然，在相似度矩阵的计算效率上，本文所提出的方案有明显的优势，不难看出，随着用户数的增大，数据量不断增长，本文所提出的方案的优势也更加显著。

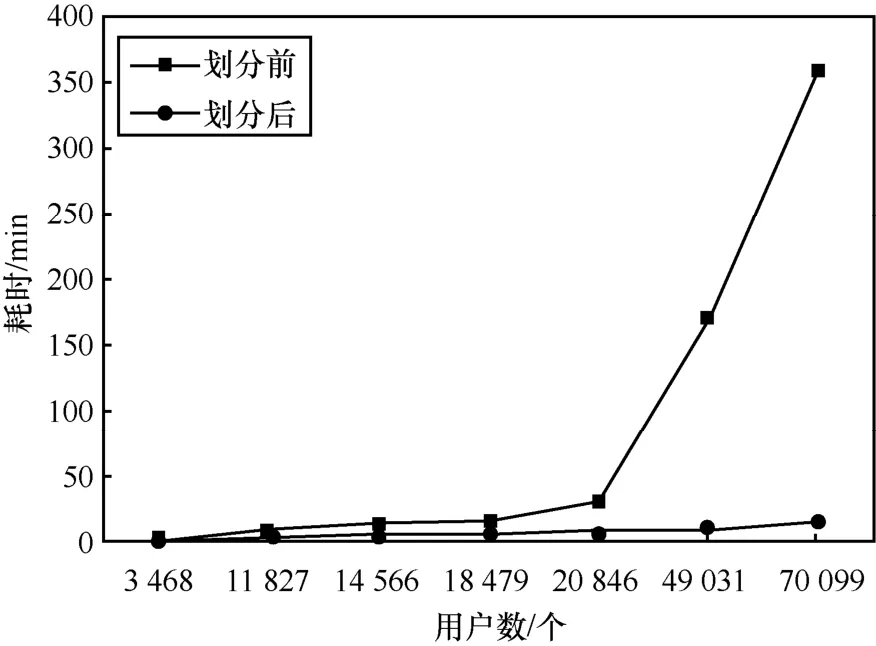
图5 不同用户数划分前后相似矩阵计算耗时

划分前后的社区发现结果准确度对比见表 3和表4，本文选取3 468个用户和20 846个用户的社区发现结果进行对比。

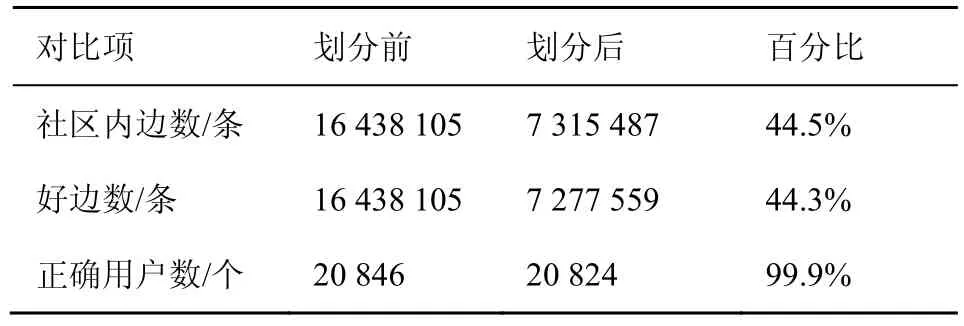
表3 20 846个用户划分前后社区发现效果对比

表4 3 468个用户划分前后社区发现效果对比

可以看出，无论是在20 846个用户还是3 468个用户的对比实验中，划分后的社区内连边数较划分前的社区内连边数都减少了近一半，而用户正确率均在95%以上，在20 846个用户的实验中，正确率甚至高达 99.9%。显然，本文所提出的相似矩阵计算方法相较于原始计算方法而言，在社区发现结果上几乎没有性能和效果的影响。

图6绘制了不同用户社区访问内容分布的热力图，可以看出，基于本文所提出的相似矩阵计算方法所获得的用户社区在访问内容分布上有明显的差异，说明该方法能够对用户内容特征实现良好的区分。

图6 不同用户社区访问内容分布

5 结束语

本文针对目前用户移动网络接入数据分析中最为常用的一种分析需求（社区发现）在面对大规模数据计算时出现的效率低下问题进行了研究，针对其主要的性能瓶颈（相似矩阵计算）进行了优化设计，提出了一种基于地理位置的分布式相似矩阵计算方法。方法利用用户移动网络接入数据中具有的先验位置信息，对用户进行基于地理位置的划分，并根据划分的结果，对用户间进行有选择性的相似度计算。相较于传统的相似度计算方法，本方法在效率上有了极大的提升，而在社区发现结果上与划分前相比达到了99.9%的一致性，整体上表现出了较为出色的性能。

根据不同数据类型的特点，有针对性地利用数据的先验知识对数据进行简单的预处理将能够为数据的后续处理带来极大的效率提升，如何将这种思想应用到更为广泛的领域中是未来需要思考的问题。

参考文献：

[1]SCRIPPS J, TREFFTZ C.Parallelizing an algorithm to find communities using the Jaccard metric[C]//IEEE International Conference on Electro/Information Technology, June 8-12,2015, London, UK.Piscataway： IEEE Press, 2015.

[2]HURLEY N, DURIAKOVA E.Reformulations of the map equation for community finding and blockmodelling [C]//IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining, August 25-28, 2015, Paris,France.Piscataway： IEEE Press, 2015.

[3]RESTREPO A, SOLANO A, SCRIPPS J, et al.High-performance implementations of a clustering algorithm for finding network communities[C]//IEEE International Conference on Electro/Information Technology, May 6-8, 2012, Indianapolis, USA.Piscataway： IEEE Press, 2012.

[4]GUNTHER J H, HOFFMAN K H.Numerische mathematik [M].Berlin： Springer, 1991.

[5]STEWART G W.Jampack： a Java package for matrix computations[EB].2017.

[6]JOE H, CLEVE M, PETER W.JAMA： a Java matrix package[EB].2017.

[7]NGUYEN D K, LAVALLEE I, BUI M, et al.A general scalable parallelizing of strassen’s algorithm for matrix multiplication on distributed memory computers[C]//ACIS International Conference on Computer and Information Science, July 14-16, 2005, Washington, DC, USA.Piscataway： IEEE Press, 2005.

[8]LIN C, HUANG Z H, YANG F, et al.Identify content quality in online social networks[J].IET Communications, 2012, 6(12)：1618-1624.

[9]孙远帅, 陈垚, 官新均, 等.基于Hadoop的大矩阵乘法处理方法[J].计算机应用, 2013, 33(12)： 3339-3344.SUN Y S, CHEN Y, GUAN X J, et al.Approach of large matrix multiplication based on Hadoop[J].Journal of Computer Applications, 2013, 33(12)： 3339-3344.

[10]REZA M, SINHA A, NAG R, et al.CUDA-enabled Hadoop cluster for sparse matrix vector multiplication[C]//IEEE International Conference on Recent Trends in Information Systems, July 9-11, 2015, Kolkata, India.Piscataway： IEEE Press,2015.

[11]MALYSIAK D, KOPINSKI T.A generic and adaptive approach for workload distribution in multi-tier cluster systems with an application to distributed matrix multiplication[C]//IEEE International Symposium on Computational Intelligence and Informatics, November 19-21, 2015, Budapest, Hungary.Piscataway： IEEE Press, 2015.

[12]GIZA-BELCIUG F, PENTIUC S G.Parallelization of similarity matrix calculus in ontology mapping systems[C]//Roedunet International Conference-Networking in Education and Research,September 24-26, 2015, Craiova, Romania.Piscataway： IEEE Press, 2015.

[13]ZHANG R, WANG Y.An enhanced agglomerative fuzzyk-means clustering method with MapReduce implementation on Hadoop platform[C]//International Conference on Progress in Informatics and Computing, May 16-18, 2014, Shanghai, China.Piscataway： IEEE Press, 2014.

[14]MANN K S, KAUR N.Cloud-deployable health data mining using secured framework for clinical decision support system[C]//International Conference and Workshop on Computing and Communication, October 15-17, 2015, Vancouver, BC,Canada.Piscataway： IEEE Press, 2015.

[15]SHAHRIVARI S, JALILI S.Single-pass and linear-timek-means clustering based on MapReduce[J].Information Systems, 2016(60)： 1-12.

[16]LU S, TONG W, CHEN Z.Implementation of theKNN algorithm based on Hadoop[C]//International Conference on Smart and Sustainable City and Big Data, July 26-27, 2015, Shanghai,China.Birmingham： IET Press, 2015.

[17]SONG G, ROCHAS J, BEZE L, et al.Knearest neighbour joins for big data on MapReduce： a theoretical and experimental analysis[J].IEEE Transactions on Knowledge & Data Engineering, 2016, 28(9)： 2376-2392.

[18]MIEGHEM P V, BLENN N, DOERR C.Lognormal distribution in the digg online social network[J].European Physical Journal B, 2011, 83(2)： 251-261.

[19]MAHANTI A, CARLSSON N, MAHANTI A, et al.A tale of the tails： power-laws in internet measurements[J].IEEE Network, 2013, 27(1)： 59-64.

[20]ZHOU C, JIANG H, CHEN Y, et al.TCB： a feature transformation method based central behavior for user interest prediction on mobile big data[J].International Journal of Distributed Sensor Networks, 2016, 12(9).

[21]WU L, JIANG H, ZHENG H, et al.Long tail and small world characteristic of mobile internet traffic dynamics[C]//IEEE International Conference on Systems, Man and Cybernetics, October 5-8, 2014, San Diego, CA, USA.Piscataway： IEEE Press, 2014.

[22]WU L, LI Y, ZHOU C, et al.Statistic analysis of data access behavior in the mobile internet[C]//IEEE/CIC International Conference on Communications in China, August 12-14, 2013,Xi’an, China.Piscataway： IEEE Press, 2013.

[23]ZHANG N, ZHENG G, CHEN H, et al.HBaseSpatial： a scalable spatial data storage based on HBase[C]//IEEE International Conference on Trust, Security and Privacy in Computing and Communications, September 24-26, 2014, Beijing, China.Piscataway： IEEE Press, 2014.

[24]王荣.基于三元组表表示的稀疏矩阵的快速转置算法及其改进[J].现代电子技术, 2008, 31(22)： 78-79.WANG R.Improvement on fast transposition algorithm to sparse matrix expressed by triple list [J].Modern Electronics Technique, 2008, 31(22)： 78-79.

[25]AFSHANG M, DHILLON H S, CHONG P H J.Fundamentals of cluster-centric content placement in cache-enabled device-to-device networks[J].IEEE Transactions on Communications, 2015, 64(6)： 2511-2526.

[26]ZHOU B, CUI Y, TAO M.Stochastic content-centric multicast scheduling for cache-enabled heterogeneous cellular networks[J].IEEE Transactions on Wireless Communications,2016, 15(9)： 6284-6297.