正弯矩作用下外伸端板连接钢管混凝土节点的承载力计算

王冬花，亓 萌,2

（1.安徽工商职业学院 会计学院，安徽 合肥 231131；2.合肥工业大学 土木与水利工程学院，安徽 合肥230009）

端板连接钢管混凝土组合节点［1］是钢-混凝土组合梁与钢管混凝土柱通过端板和单边高强螺栓连接而成，主要连接形式有外伸端板连接和平齐端板连接两种类型.组合节点区区域楼板内设置连续抗剪栓钉和贯穿钢筋来保证组合节点的组合效应.有研究表明［2］此类组合节点具有良好的半刚性，其施工快捷方便、受力性能和抗震性能好，且造价较低.

近年来国内外学者对外伸端板连接的钢-混凝土组合梁与H型钢柱连接组合节点进行了试验研究，并提出了负弯矩作用下此类节点的抗弯承载力简化计算方法［3-6］.目前对外伸端板连接钢-混凝土组合梁与钢管混凝土柱组合节点的试验和理论研究较少见，仅澳大利亚Loh等［7］、中国王静峰等［8］开展了端板连接钢管混凝土组合节点的拟静力试验研究，针对正弯矩作用下外伸端板连接钢管混凝土组合节点的可能失效模式，提出对称荷载和非对称荷载作用下组合节点的力学模型和各组件承载力简化计算方法，给出了正弯矩作用下外伸端板连接组合节点的抗弯承载力计算公式，并通过试验结果进行了验证.

1 正弯矩作用下组合节点的力学模型

端板连接钢管混凝土组合节点的拉力主要由螺栓承担，压力主要由钢梁上翼缘、柱腹板壁、混凝土楼板局部受压承担.在非对称荷载作用下，除对称荷载作用下的受力外，还受到节点域腹板剪力作用.

外伸端板连接组合节点，在对称荷载（正弯矩M1）和非对称荷载（正弯矩M1和M2，其中M1＞M2）作用下组合节点的力学模型见图1.通过组合节点的力学模型，可以获悉其拉、压组件和受力关系.

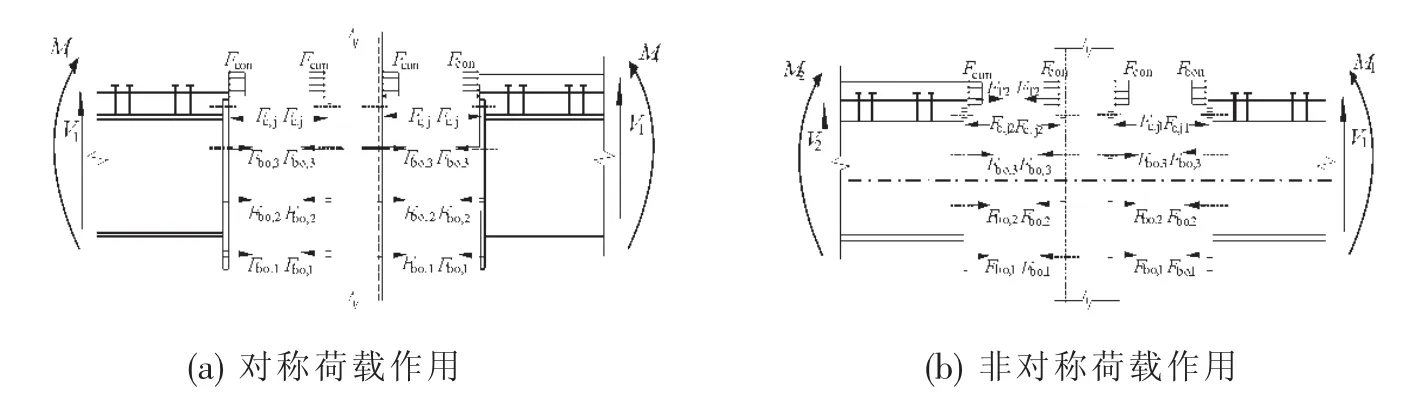
图1 力学模型

2 正弯矩作用下组合节点的抗弯承载力

为了得到正弯矩作用下该组合节点的抗弯承载力计算公式，假设有n排单边螺栓连接此组合节点，根据6种不同的塑性中和轴的位置进行了以下划分.

第一种情况（见图2）：钢梁下翼缘上第一排至第m-1排螺栓全部受拉，第m排螺栓只有部分受拉，其内力没有达到极限抗拉承载力Fbo,c.

在此情况下，钢梁腹板的受压区高度满足式（1）：

式中：lm为第m排螺栓中心至混凝土楼板与H型钢梁翼缘相接触的距离，xc,bw,i为第i排螺栓受拉时，H型钢梁腹板相对受压区高度，Fc,j为正弯矩作用下连接抗压承载力，Fbo为螺栓的抗拉承载力，hs1为混凝土楼板的总高度，tbf为H型钢梁翼缘的厚度，tbw为H型钢梁腹板的厚度，f′y,bw为考虑剪力影响的H型钢梁腹板强度，按式（2）确定：

式中：fy,bw为H型钢梁腹板的屈服强度，τxy为H型钢梁腹板内的剪应力，按式（3）计算：

式中：V为作用在连接处剪力，hbw为H型梁腹板的高度.

Fcon为混凝土楼板与柱翼缘接触处的局部抗压承载力，按式（4）计算.

式中：fcu为钢管柱混凝土立方体抗压强度；hs1,cf为钢管混凝土柱与混凝土楼板相接触处的厚度，bcf为钢管柱截面宽度，β为混凝土局部受压强度的增大系数，建议取1.25.

H型钢梁腹板受压区边到腹板上翼缘的距离即实际相对受压区高度为：

式中：pb为第一排单边高强螺栓到组合梁下翼缘上表面的距离，hb为H型钢梁截面高度，p为螺栓各排的间距.在此情况，受压的是1～m排螺栓，第m排螺栓的抗拉承载力Fbo,m应按式（6）计算：

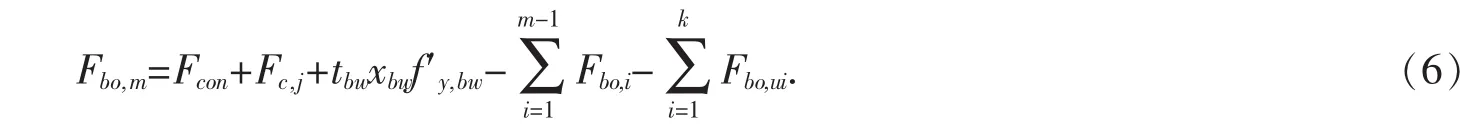
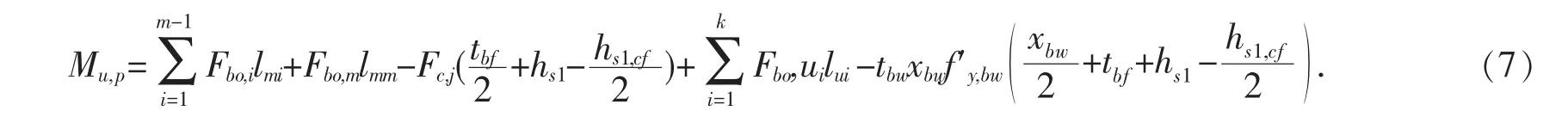
正弯矩作用下此类组合节点的抗弯承载力为：式中：lmi为混凝土楼板受压区中心至第i排螺栓中心的距离，i=1,2,…,n；lui为混凝土楼板受压区中心至第i排外伸出H型钢梁下翼缘高强螺栓中心的距离，i=1,2,…,n.

第二种情况（见图3）中和轴位于钢梁腹板内，第一排至第m排螺栓全部受拉.

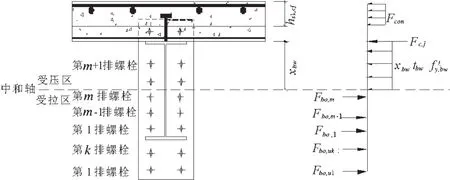
图3 第二种中和轴位置

此种情况在实际工程中较为常见，塑性中和轴位于H型钢梁腹板内，部分螺栓位于受压区内.组合节点的受力平衡方程为：

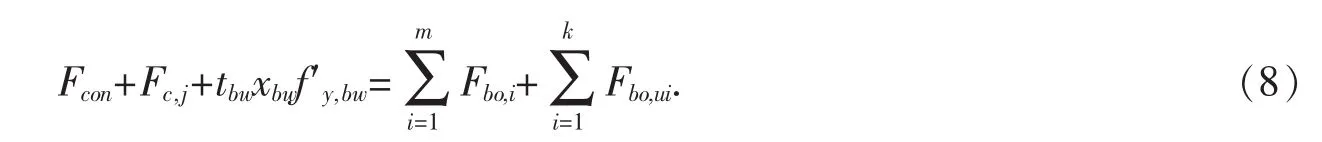
根据平衡条件，钢梁腹板的受压区高度为：

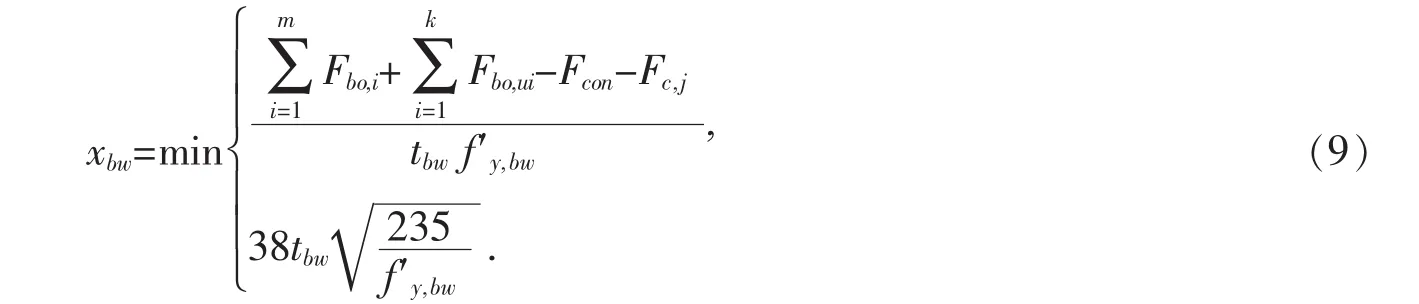
此时对H型钢梁上方的受压混凝土楼板中心求矩，则此组合节点的抗弯承载力：

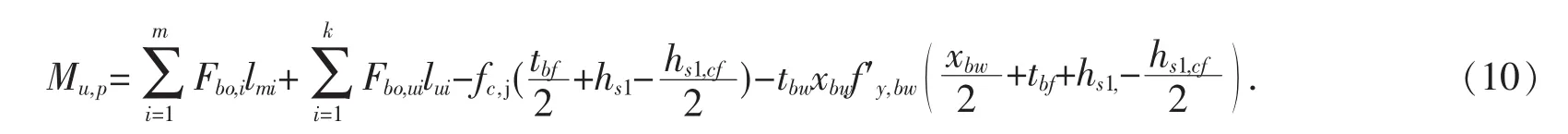
第三种情况（见图4）：位于H型钢梁上翼缘下方的螺栓全部受拉，塑性中和轴位于H型钢梁腹板内.

此种情况出现在螺栓的抗拉承载力较低或混凝土楼板过厚时，实际工程中较少发生.此时位于H型钢梁上翼缘下方螺栓都是处于受拉区域，且内力都达到了其极限抗拉承载力.在此情况下，受力平衡方程为：

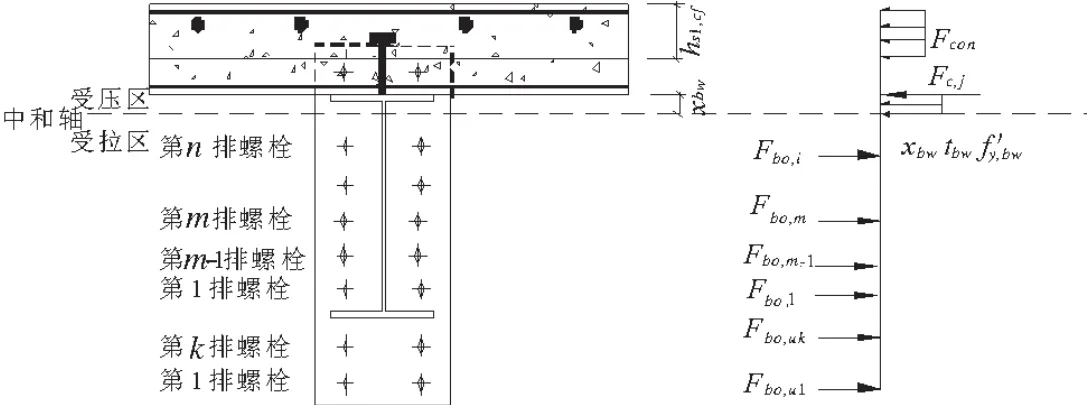
图4 第三种中和轴位置

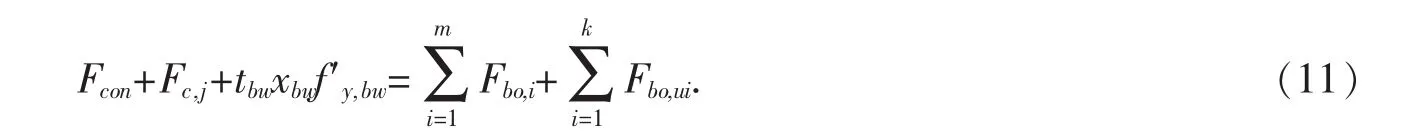
钢梁腹板的受压区高度为：

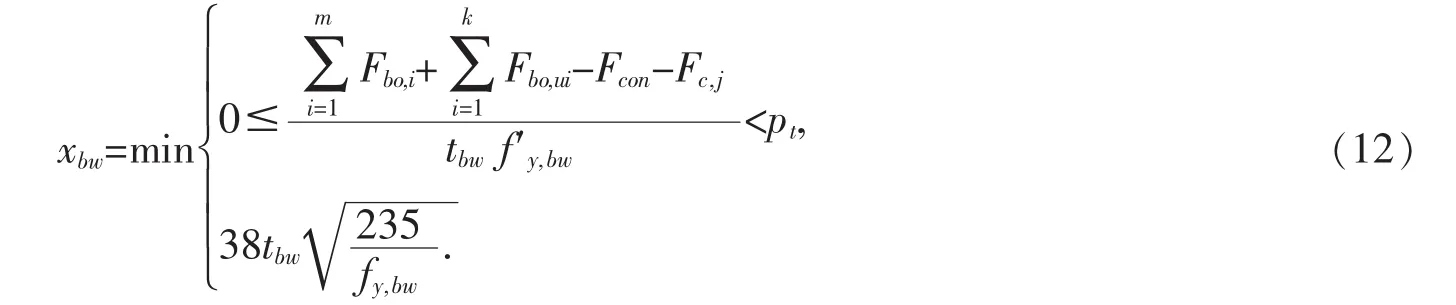
式中：pt为H型钢梁上翼缘下表面至第n排螺栓的距离.

在此情况下，对受压区混凝土楼板中心求矩，则此类组合节点的抗弯承载力为：

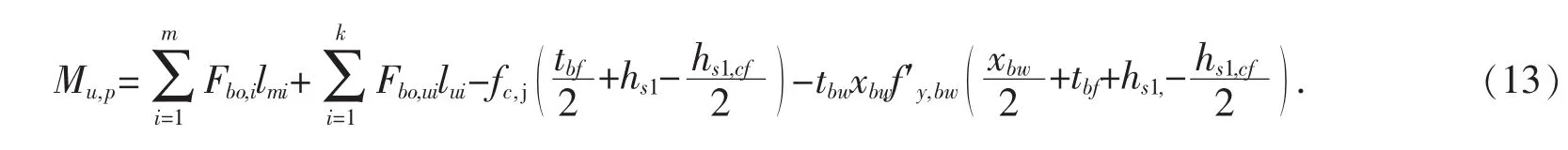
第四种情况（见图5）：中和轴位于钢梁上翼缘.

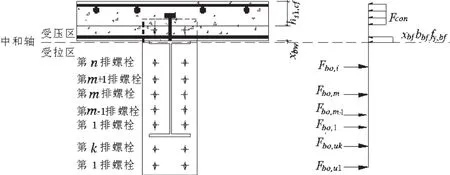
图5 第四种中和轴位置

此种情况出现在螺栓的抗拉承载力较低或混凝土楼板过厚，在实际工程中极少发生.此时位于H型钢梁上翼缘下方螺栓都是处于受拉区域，且内力都达到了其极限抗拉承载力.

钢梁上翼缘所承受压力按下式确定：

此时所有螺栓均位于受拉区，则：

式中：fy,bf为梁翼缘屈服强度，bbf为钢梁翼缘宽度.则钢梁上翼缘的受压区高度为：

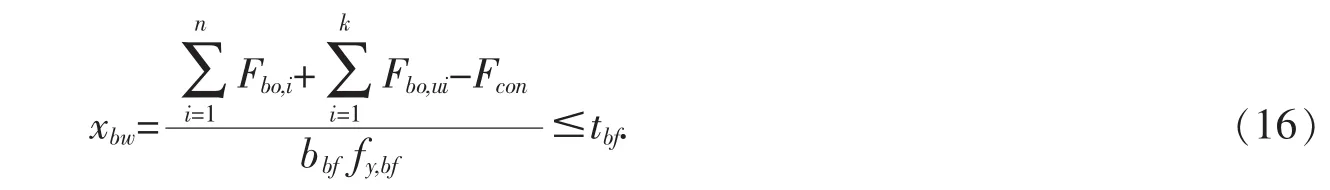
在此情况下，对受压区混凝土楼板中心求矩，则此类组合节点的抗弯承载力为：

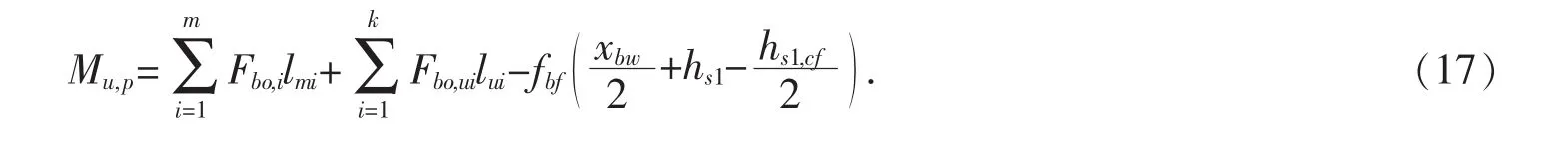
第五种情况（见图6）：中和轴位于钢梁上翼缘上方的混凝土楼板内.

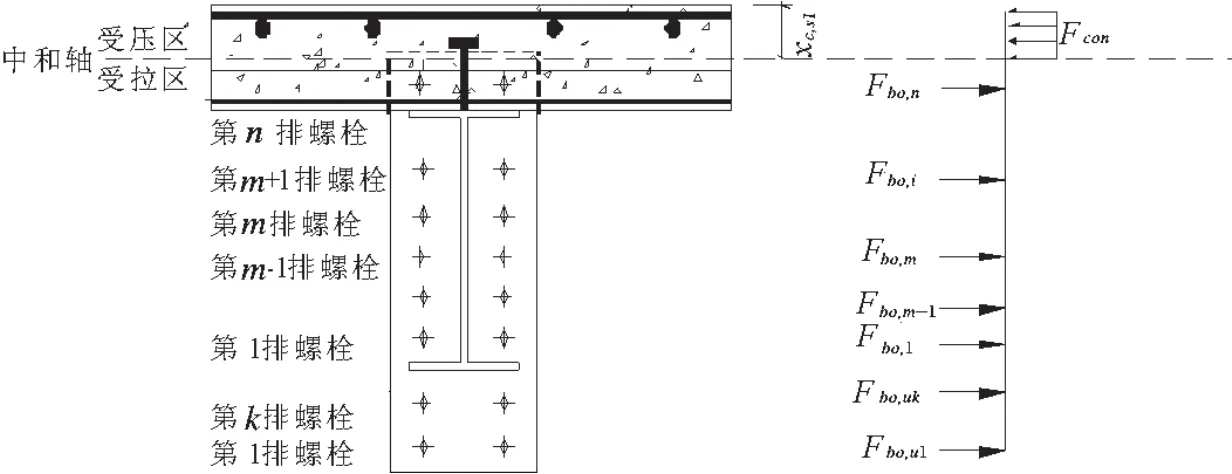
图6 第五种中和轴位置

在实际工程相对于第三、第四种塑性中和轴位置来说更为少见，只有在螺栓的抗拉承载力极低或混凝土楼板特别厚才会发生，位于中和轴下方螺栓全部处于受拉区域，且内力都达到了其极限抗拉承载力.

此时受力平衡方程为：

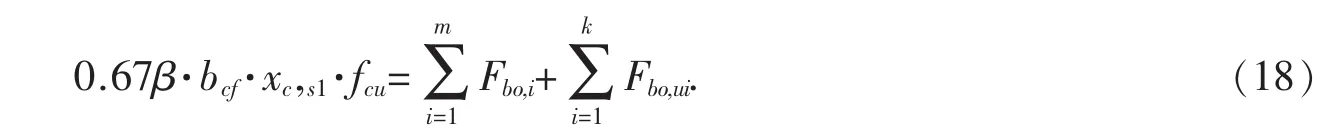
由此可计算混凝土楼板相对受压区高度，xc,s1为：

在此情况下，对受压区混凝土楼板中心求矩，则此类组合节点的抗弯承载力为：

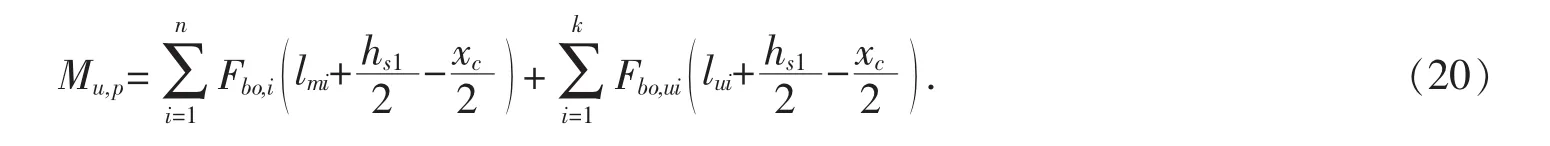
第六种情况（见图7）：中和轴位于钢梁下翼缘.这种情况只有在螺栓的抗拉承载力极强得情况下才会发生，H型钢梁下翼缘下的螺栓全部处于受拉区域，此时受力平衡方程为：

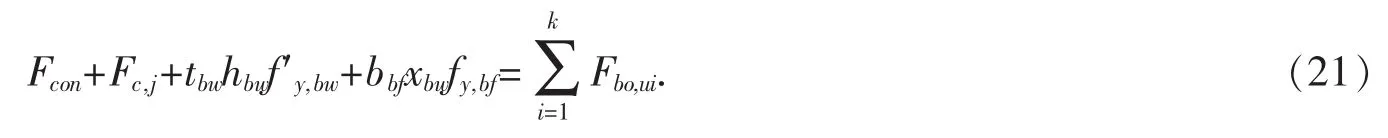
式中：hbw为H型钢梁腹板高度.

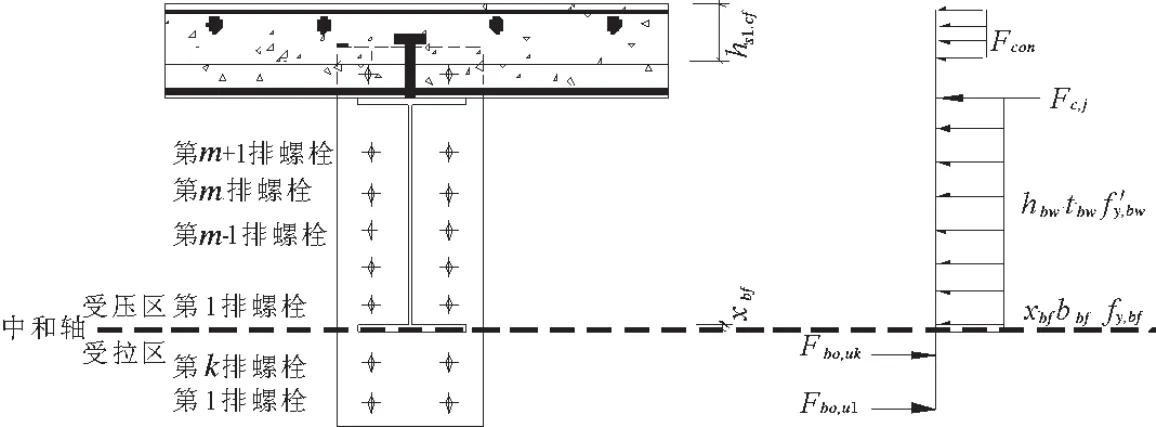
图7 第六种中和轴位置

钢梁上翼缘所承受压力Fc,bf为：

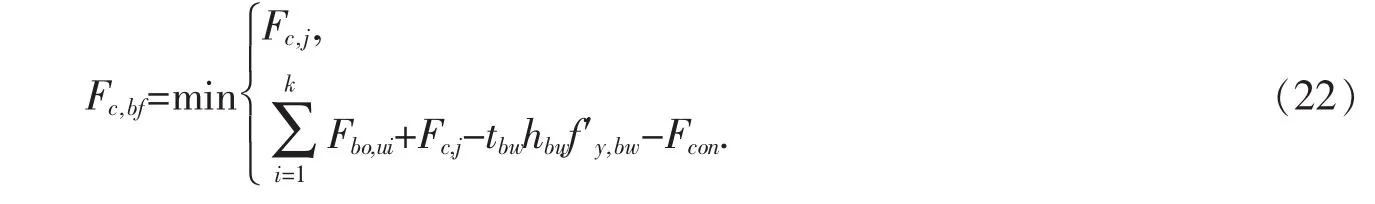
则钢梁下翼缘的受压区高度为：

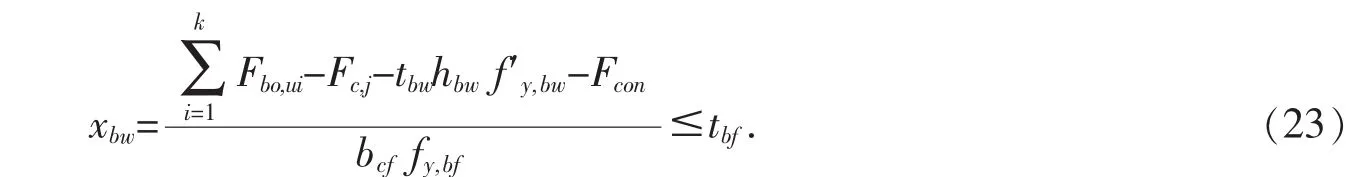
在此情况下，对受压区混凝土楼板中心求矩，则此类组合节点的抗弯承载力为：

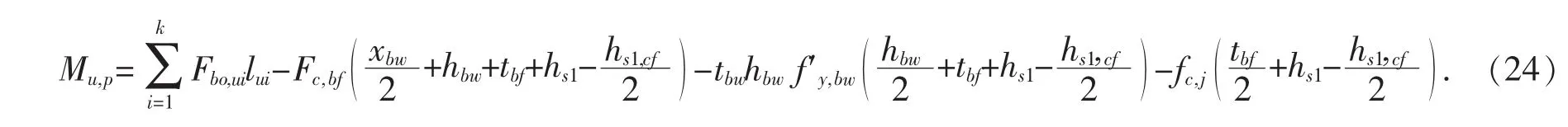
3 试验验证

对比了外伸端板连接钢管混凝土组合节点在正弯矩作用下抗弯承载力计算公式和2榀带楼板平齐端板连接钢管混凝土组合节点试验［8］结果.试件的详细尺寸信息见图8.试验采用10.9级M20单边螺栓，单边螺栓性能及其构造见文献［8］.试件具体安装见文献［2］.试验程序采用美国ATC-24加载制度.主要量测了组合节点侧向位移、柱水平位移、柱端水平荷载，核心节点区楼板内纵向钢筋、H型钢梁、端板和钢管的应力分布.

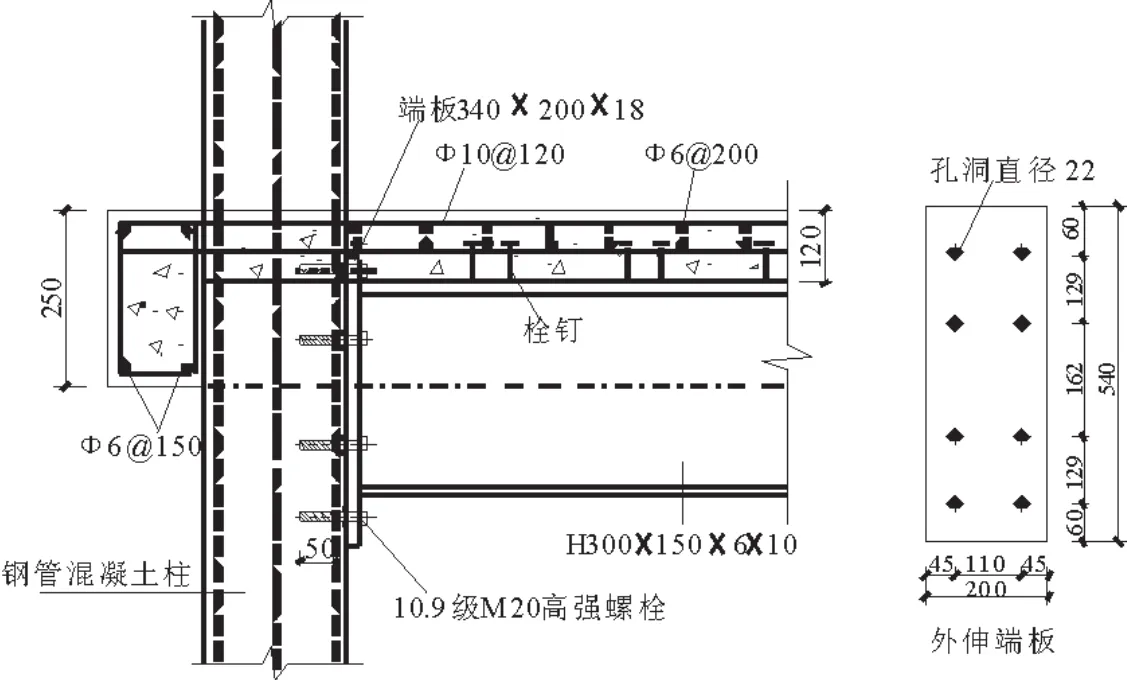
图8 试件尺寸详图

计算结果与试验结果对比如表1所示.从表1可以看出，试验值比计算值大16%～26%，说明所得简化计算方法的具有一定得准确性，且偏于保守.

表1 试验结果与计算结果比较

4 结语

基于力学平衡原理，利用塑性分析方法，考虑不同塑性中和轴位置，获得了在正弯矩作用下此类组合节点的承载力计算方法.并将其与试验结果进行了比较，从比较的结果可以看出，本文所提的简化计算方法具有一定得准确性，在外伸端板连接的钢管混凝土组合框架设计中可以应用此公式.如果不考虑楼板影响，该方法也可以计算端板连接钢管混凝土框架节点的抗弯承载力.

［1］Nakashima M,Bruneu M.English edition of preliminary reconnaissance report of the 1995 Hyogikerr Nanhu earthquake［R］.Toyko:The Architectural Institute of Japan,1995.

［2］姜涛．半刚性钢管混凝土组合框架节点的抗震性能及设计方法［D］.合肥：合肥工业大学，2012.

［3］石文龙．平端板连接半刚性梁柱组合节点的试验与理论研究［D］.上海：同济大学,2006.

［4］董硕.正弯矩作用下平齐端板连接组合节点的实验研究［D］.南京：南京工业大学,2006.

［5］Liew J Y R,Teo T H，Shanmugam N E,et al.Testing of steel-concrete composite connection and appraisal of results［J］.Journal of Constructional Steel Research,2000,56(2):117-150.

［6］Li T Q,Nethercot D A,Choo B S.Behavior of flush end-plate composite connections with unbalanced moment and variable shear/moment ratios--II.Prediction of moment capacity［J］.Journal of Constructional Steel Research,1996,38(2):165-198.

［7］Loh H Y,Uy B,Bradford M A.The effects of partial shear connection in composite flush end plate joints:Part I-experimental study［J］.Journal of Constructional Steel Research,2006（62）:378-390.

［8］王静峰，龚旭东，姜涛，等.钢管混凝土边柱与组合梁端板连接的抗震试验研究［J］.土木工程学报,2013,46(11):44-53.