第二十四讲 混料组合均匀设计
2018-05-25徐静安段敏伟
徐静安 段敏伟
2014年的8月19日是地球超载日。杨维成、段敏伟来我办公室讨论甲醇柴油微乳化混料试验方案,涉及DPS数据处理系统,我的电脑中存有蛇年(2013年)张玉梅给我下载的电子版。两位青年同仁得知我眼睛老花加散光阅读电子版较累,提出把纸质版的书送给我,因他们更需要学习而被我婉拒。8月25日,段敏伟来我办公室谈及开发中心已订购正版DPS软件,附赠纸质版的新版《DPS数据处理系统——实验设计、统计分析及数据挖掘》(唐启义著),所以代表罗勇、杨维成把现有第2版的专著送给我,不会影响学习。喜得此书后,再一次浏览全书(1 138页)。
序二同行评价DPS分析软件“开发了具有全球领先地位的均匀试验设计、混料试验设计、动态聚类分析几个功能模块的独创算法”。对此相应章节结合院内项目案例进行了精读。
笔者在1987年12月6日于北京王府井购买的《试验优化技术》一书中初次接触“均匀设计”、“混料回归设计”等。陈涛是上海化工研究院较早在阻燃剂技术开发中应用混料回归设计中的“极端顶点设计”的,我还在他那儿借阅过《六西格玛管理统计指南——MINITAB使用指导》,阅后于2008年我去上海书城购得,再读,此后建议院部购买一批在科技人员中发放。
自2014年10月份以来,段敏伟平均十天半月讨论一次混料试验方案,期间阅读了上述几本书,并学习了其中的典型案例,对混料试验设计的传统方法、经典方法、混料均匀设计方法有所了解,有了和笔者合作、开发应用混料组合均匀设计方法的基础。
一、有过程参数的混料均匀设计
在工程混料试验中,往往涉及到混料配方反应的温度、压力、时间以及配方在基料中的添加量等这些过程参数(变量)。在不得已的情况下,过去采用固定这些过程参数来对混料配方试验作出评价,实际上默认这些过程参数对混料配方的交互作用不作考虑,并认为考察范围是单峰函数。如对一些重要的混料配方试验,必须考察其交互作用,就采用优化试验中的“转轴法”思想,分段轮换考察:初定过程参数,考察混料配方——选定混料配方,考察完善过程参数——固定完善后的过程参数,优化混料配方。显然实验工作量是很大的,尤其是在多目标响应Y有多个技术指标约束时,数据的分析处理会带来困难。所以实际研究工作往往是满足于获得“可用的配方”,不得已而为之。
把过程参数变量和混料配方组分组合在一起的均匀设计,就构筑成混料组合均匀设计。
现代应用数学方法丛书7之《正交与均匀试验设计》(方开泰、马长兴著,科学出版社2001年出版),在“均匀设计应用的广泛性”、“混合类型因素的试验”中,提出基于均匀设计Un(nl)表构筑混料组合均匀设计的思想。
《DPS数据处理系统——实验设计、统计分析及数据挖掘》(唐启义著,科学出版社2010年出版)在“偏最小二乘回归分析”混料试验数据建模的案例中,展示了含过程变量的混料试验的数据处理。
对于数理统计学家,混料组合均匀设计在学术上似乎已经解决,没有进一步展开讨论,但在工程界应用、构筑试验设计方案时还存在一些不够方便的“坎”,所以应用不够广泛。
二、混料组合均匀设计方案构筑
对于混料组合均匀设计,过程变量是独立的,混料配方存在∑Xi=1的约束。所以如本刊2018年第二期刊登的第二十二讲“混料均匀设计简介”中叙述,需对均匀表中混料配方所占列进行逆变换。
现以1个过程变量,P=3可转换成正单形的混料试验为例,构筑设计方案。
本例考察的过程变量数C=1,配方变量数P-1=3-1=2,所以首先要选择一个均匀设计表Un(n3)。
均匀设计一般要求试验次数n≥2~2.5倍考察变量数,而经典的混料回归设计试验次数n≥3~5倍考察变量数。本案例取n=7,选用U7*(74)表,根据使用表,过程变量安排在第2列,将混料配方P-1=2分别安排在3,4列。具体见表1~2。

表1 U7*(74)

表2 U7*(74)的使用表
用{qji}表示所选均匀表第j列中的第i(i=1,2,…,n)个元素进行转换。

将{Cji}转换成{Xji}
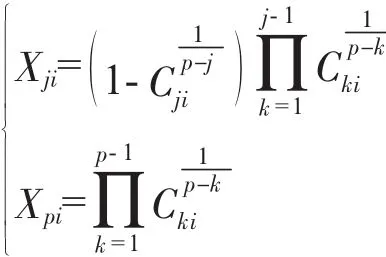
式中:Π为连乘符是Cji的次方数。
计算详见本刊2018年第二期刊登的第二十二讲“混料均匀设计简介”。笔者为了加深对此变换的理解,本着“眼过千遍,不如手过一遍”的古训,用手机上的计算器模块作了逐项计算,构筑成表3。

表3 用计算器模块作逐项计算结果
在单纯混料均匀设计中,介绍均匀设计U7*(74)表变换成UM7*(73)混料均匀表的过程。U表示均匀设计,M 为混料试验,n=7(实验次数),np=73,为P=3的三组分配方试验。专著中没有对混料组合均匀设计明确命名,笔者按此思路建议:
均匀设计U7*(74)表变换成混料组合均匀设计UCM7*(71+3)表,其中:C表示组合过程变量;nc+p=71+3,上角码C表示组合的过程变量数,P表示配方的组分数。
在上表中,为了和UMn*(np)表对应,C1,C2变换成(x1)、(x2)、(x3),由于有过程变量,在UCM7*(71+3)中应为 X2,X3,X4。而统计建模时,通用方法仅 X1,X2,X3进入模型。
三、常用混料组合均匀设计表
为了便于应用,段敏伟通过DPS数据软件对U7*(74)变换成UCM7*(71+3)等,详细步骤如下:
在变换前,先将需要变换的U7*(74)表第3,4列输入到DPS软件的电子表格中,并按照图1所示定义成数据块。(备注:在DPS V14.50版本中,由于软件存在缺陷,经与唐启义老师沟通后,数据块需要多选择一列空列)。然后执行DPS“混料试验设计”里面的“混料均匀设计”功能模块即可得到如图2所示的混料均匀设计。上述计算结果和笔者按方开泰提出的变换公式用手机计算器计算得到的结果一致,仅个别数据末位由于进位精度存在0.000 1的差异。常用混料组合均匀设计见表4~5。

图1 通过DPS数据软件定义成数据块


图2 混料均匀设计
1 U10*(108)变换成UCM10*(101+3)
过程变量C=1、配方因素数P=3,查U10*(108)的使用表,选择第1,5,6列,过程变量安排在第1列,将混料配方P-1=2分别安排在第5,6列。对第5,6列采用DPS软件及上述步骤进行变换,从而得到了UCM10*(101+3)表(见表6)。

表4 U10*(108)

表5 U10*(108)的使用表
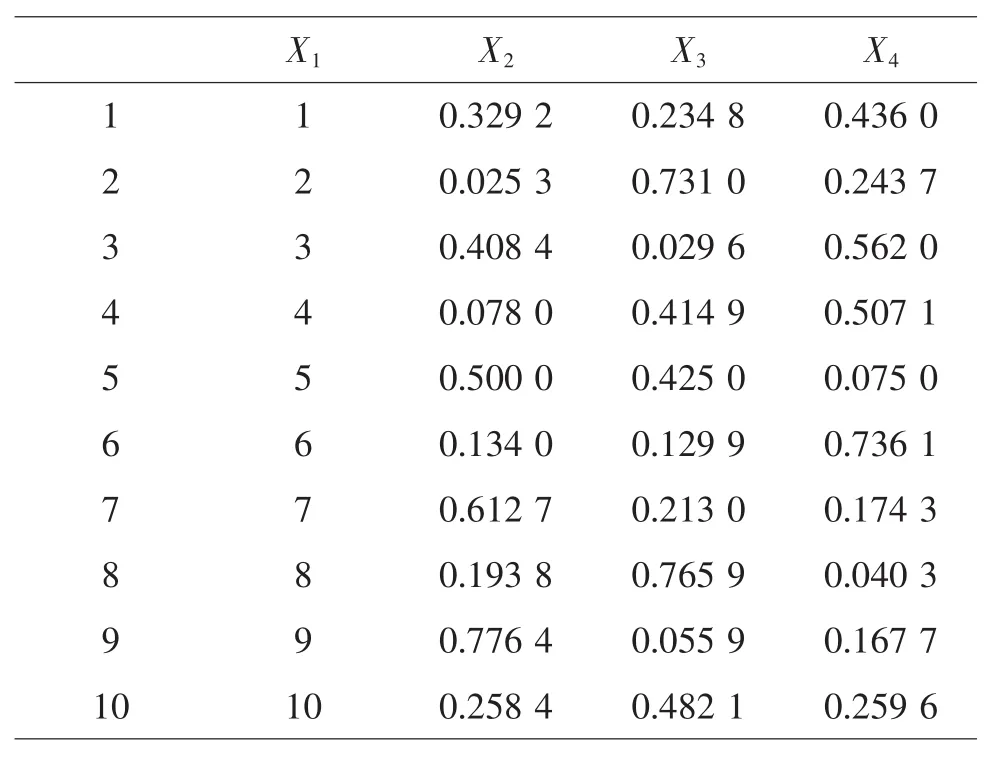
表6 UCM10*(101+3)
2 U10*(108)变换成UCM10*(101+4)
由于配方因素数P=4,查U10*(108)的使用表,选择1,3,4,5列,过程变量安排在第1列,将混料配方P-1=3 分别安排在 3,4,5 列。对第 3,4,5 列进行变换,得到UCM10*(101+4)表(见表7)。
3 U10*(108)变换成UCM10*(101+5)
由于配方因素数P=5,查U10*(108)的使用表,选择 1,3,4,5,7 列,过程变量安排在第 1 列,将混料配方 P-1=4 分别安排在 3,4,5,7 列。对第 3,4,5,7 列进行变换,得到UCM10*(101+5)表(见表8)。

表7 UCM10*(101+4)

表8 UCM10*(101+5)
4 U10*(108)变换成UCM10*(102+3)
虽然配方因素数P=3,但由于过程变量为2,使用表因素应为C+P-1=4,查U10*(108)的使用表,选择1,3,4,5 列,过程变量安排在第 1,3 列,将混料配方P-1=2分别安排在4,5列。对第4,5列进行变换,得到UCM10*(102+3)表(见表9)。
5 U10*(108)变换成UCM10*(102+4)
使用表因素应为C+P-1=5,查U10*(108)的使用表,选择 1,3,4,5,7 列,过程变量安排在第 1,3 列,将混料配方P-1=3分别安排在4,5,7列。对第4,5,7列进行变换,得到UCM10*(102+4)表(见表10)。
6 U10*(108)变换成UCM10*(102+5)
使用表因素应为C+P-1=6,查U10*(108)的使用表,选择 1,2,3,5,6,8 列,过程变量安排在第 1,2列,将混料配方P-1=3分别安排在3,5,6,8列。对第3,5,6,8列进行变换,得到UCM10*(102+5)表(见表11)。

表9 UCM10*(102+3)

表11 UCM10*(102+5)
7 U10*(108)变换成UCM10*(103+3)
使用表因素应为C+P-1=5,查U10*(108)的使用表,选择 1,3,4,5,7 列,过程变量安排在第 1,3,4列,将混料配方P-1=2分别安排在5,7列。对第5,7列进行变换,得到UCM10*(103+3)表(见表12)。
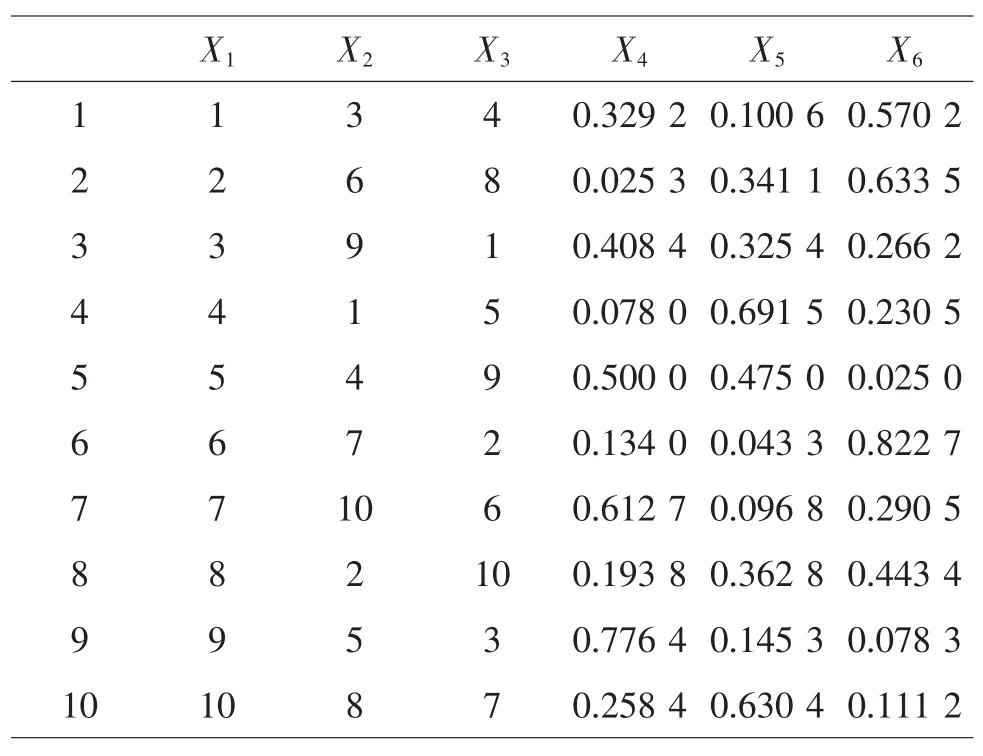
表12 UCM10*(103+3)
8 U10*(108)变换成UCM10*(103+4)
使用表因素应为C+P-1=6,查U10*(108)的使用表,选择 1,2,3,5,6,8 列,过程变量安排在第 1,2,3列,将混料配方P-1=3分别安排在5,6,8列。对第5,6,8列进行变换,得到UCM10*(103+4)表(见表13)。
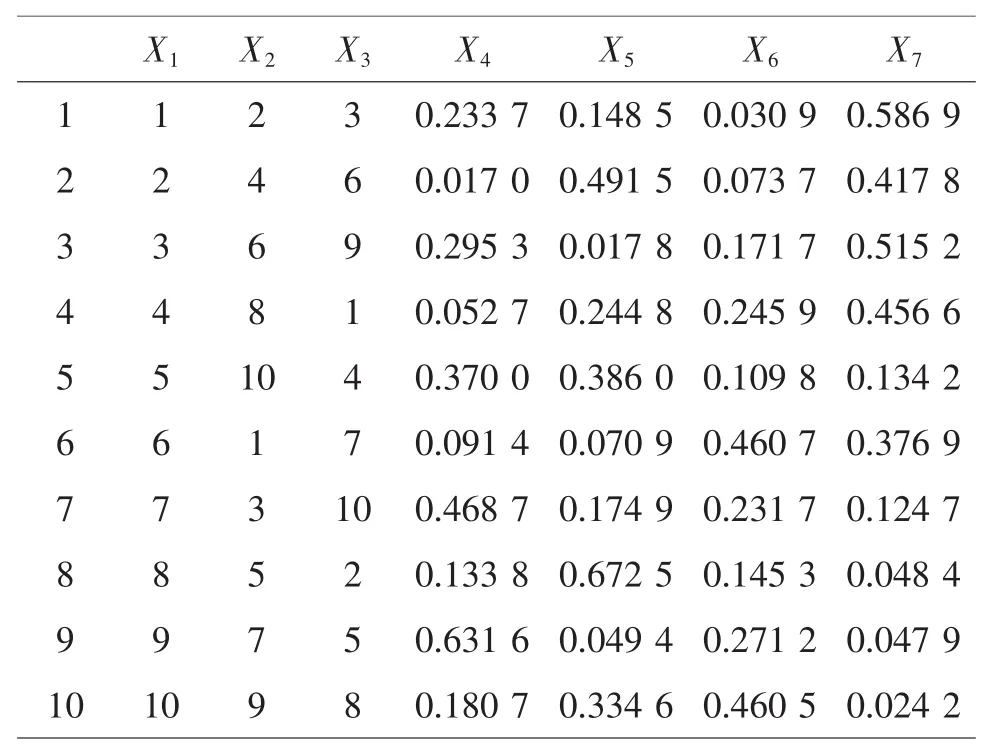
表13 UCM10*(103+4)
需要特别强调的是本文和本刊2018年第二期刊登的第二十二讲“混料均匀设计简介”是上下篇,对于混料配方部分适用于无约束、下限约束以及有上下限约束但可调整为正单形的混料试验。对于不能调整为正单形的有上下限约束的混料试验,我们还将进一步介绍和讨论。
本文定稿于2015年元旦,窗外阳光明媚。
