第二十一讲 混料配方研究中极端顶点设计的应用解读
2018-05-25徐静安许肖丽
徐静安 许肖丽 陈 涛
在科学研究和工农业生产中,混料-配方问题常常被广泛涉及,如不同配比、添加剂的甲醇混合燃料、多元复合肥料、分子筛、粘接剂、复混型工程塑料(超高改性料)、合金、复配型药方、混合饲料、混凝土、电解液(超导基带抛光液)、闪光剂、洗涤剂、油漆涂料……混纺纤维、阻燃剂等。
许肖丽硕士给笔者送阅《2013年塑料助剂生产与应用技术信息交流会论文集》,浏览中读到“三邻苯二胺基环三磷腈的合成及在EVA中的阻燃研究”一文,该论文是其硕士研究生工作的一部分。因混料设计是一类带有普遍性的试验设计方法,使我产生了进一步学习、解读的冲动。自2014年7月份开始,精读了几本数理统计藏书中有关混料设计的章节。
笔者曾在1987年12月6日于北京王府井新华书店购得《试验优化技术》,初次接触均匀设计、混料回归设计等。相关资料还包括:20世纪90年代后期上海化工研究院学习班用教材《均匀设计与均匀设计表》;2008年先从陈涛硕士处借阅,又从上海书城购买的《六西格玛管理统计指南——MINITAB使用指导》;2009年从网上下载《正交与均匀试验设计》,2010年上海化工研究院科研处发放的《试验设计与数据处理》;特别是2013年所得电子版、2014年喜获纸质版的《DPS数据处理系统——实验设计、统计分析及数据挖掘(第二版)》。通过再读、比对、质疑,关于混料回归设计的应用方法更为清晰,经过反复讨论、计算对比,共同完成本文。
一、案例极端顶点试验设计方案及计算结果
膨胀型阻燃剂是酸源、碳源、气源协同作用的体系,现对聚磷酸铵(APP)、三邻苯二胺基环三磷腈(HACTP)和阻燃协效剂进行系统考察。本文重点讨论各混料组分对响应值极限氧指数(LOI)的影响。混料中各组分及相应的考察范围:
X1—APP,10%~60%;X2—HACTP,20%~80%;X3—阻燃协效剂,5%~20%。
使用MINITAB软件,得到极端顶点设计的设计方案,实验结果见案例表1。
按表1直观分析满足各项指标的“好点”,以及建模后MINITAB“响应优化器”预报力学性能的最优值工艺,进行重复、验证实验,见表2和表3。
验证结果表明,预报的IFR-优化配方的阻燃及力学性能均达到并超过相应标准的技术要求指标,为实验范围内的较优值,数据可信。
二、案例极端顶点试验设计方案解释
混料回归设计是试验设计中的一个重要分类,极端顶点设计又是混料设计中常用的方法,其设计方案涉及一些名词、术语、方法,解释如下:
1 混料试验
混料试验分量组分至少有3种(p≥3),每个组分xi的含量百分比总和等于
试验响应值y仅与xi的百分比有关,而与其总量无关。由于约束条件的存在,各分量是不独立的。和以往的试验不同,所以试验研究要用混料设计方法,才能对各组分进行系统考察。
2 单形坐标系
单形是指顶点数与坐标空间维数相等的凸图形。在单形混料设计中,一般用正单形,如正三角形、正四面体等。p维单形即(p-1)维的单纯形。案例3组分,3-1=2,即高为1的平面正三角形构成三线坐标图(见图1)。正三角形内的任意一点R都有3个坐标,且x1+x2+x3=1。用单形坐标系能确切描述混料组分间的关系。所以混料试验设计方案将在单形坐标系中展开,而以往的试验设计是基于直角坐标。如果p=4即为正四面体,p≥5无直观图形,而用数学描述。

表1 混料设计配方及测试结果

表2 验证实验配方表
3 混料设计-极端顶点法
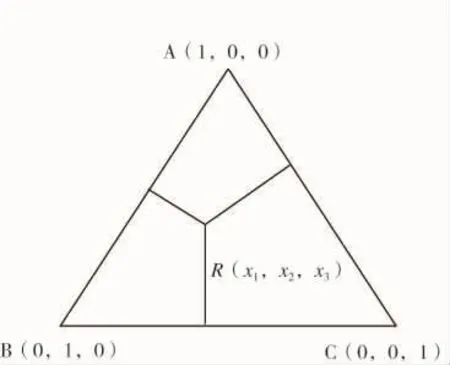
图1 三线坐标图
基于单形坐标系安排的相应试验设计,能全面考察各分量对于响应量y的影响。实验点的选取方法有单纯形质心法、单纯形格点法和极端顶点法。本论文重点讨论极端顶点法。
混料试验中,各分量还可能各自受上限bi、下限ai的约束,即:
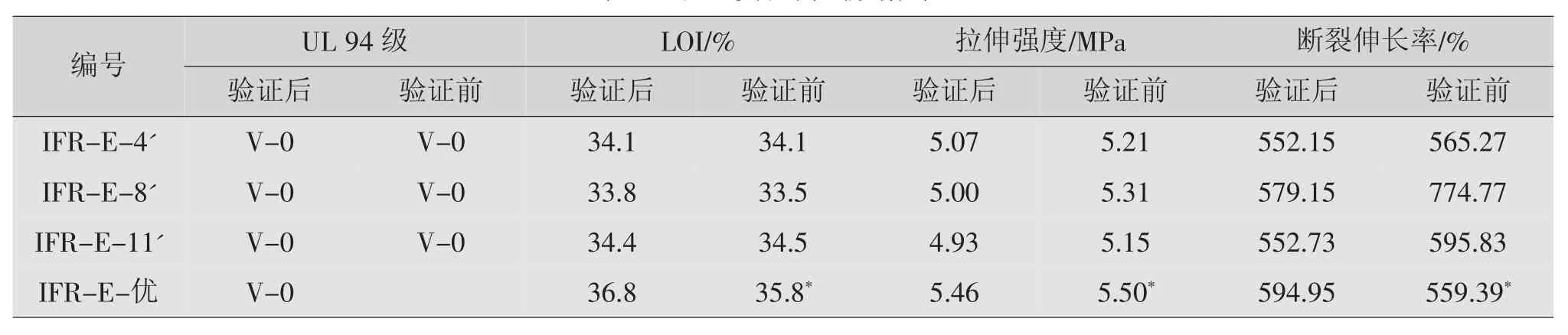
表3 验证实验测试数据对比
结合案例,p=3的单形可能形成的凸图形如图2所示。
根据上、下限约束值的不同,在三线坐标系内,实验考察范围的位置、界区、图形有所不同,但由上、下限约束线形成的凸图形顶点数可分为4类:即3顶点、4顶点、5顶点、6顶点凸图形。显然,顶点是约束线的交点,3顶点凸图形有3组3条约束线均相交于1点;4顶点凸图形有2组3条约束线相交于1点;5顶点凸图形有1组3条约束线相交于1点;6顶点凸图形顶点均为2条约束线的交点。此类由约束线形成的交点——顶点满足Σxi=1,称为极端顶点。以极端顶点点集为基础所构成的混料试验方案,称为极端顶点设计。
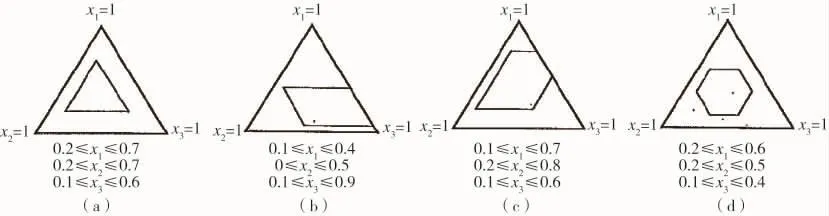
图2 4种凸图形
4 极端顶点设计增强
由于传统混料设计的数据处理采用全回归方法,如果回归模型中的未知参数个数多于极端顶点个数(实验点数)就无法求解,所以需要补充一些由极端顶点构成的棱、面、体的质心作为实验点,构成了相应的增强设计。
(1)混料设计的阶数增强
混料设计中阶数d的引入是与回归建模的d次多项式有关,一般选d=2,用二次多项式拟合,对于较复杂的研究对象d=3已经足够满足拟合精度。
由2个相邻顶点相连成棱线,选用棱线上线长处点(双混点)的点集,称该混料设计的阶数d=2,选用处的2个点的点集,则阶数d=3。混料设计表述为{p,d}。本案例为{3,2},即混料3个分量2阶极端顶点设计。顶点加上棱线上的点,构成极端顶点设计的基本点集。
如果顶点数为n,则极端顶点基本点集数为N=n+n(d-1)=nd。
(2)中心增强
由于极端顶点设计的基本点集均集中在顶点、棱线上,即实验考察范围的界面上,选择整个凸图形内唯一的质心——中心点,称为中心点增强。中心点增强能有效地提高统计建模的准确性。
采用中心增强,设计的点集数为:N=nd+1。
(3)轴点增强
鉴于相同理由,增强方向在凸图形的内部,有利于实验点集在考察凸图形范围内的均匀性。顶点和中心点连线称为轴,轴线上线长处的点为轴点,选择轴点点集称为轴点增强。
采用轴点增强,极端顶点实验设计实验点集数为:N=nd+n=n(d+1)。
本案例采用中心点、轴点双增强的极端顶点设计,案例实验点集数为:N=n(d+1)+1。5 极端顶点设计中多余约束的解除
在混料设计的单形坐标系中,对任一分量给出的上、下限约束,必然相应地、精确地转化为对另两个分量的约束。
图3所示,C分量下限约束线Ca,同时转化为A分量上限约束线Ab'。如果A分量本身的上限约束为Ab线,二者不一致,存在多余约束。在三线坐标系中,约束值Ab'<Ab,Ab约束为多余,应予以解除,其余类推。
对于极端顶点设计进一步的描述是有上下约束的混料设计,
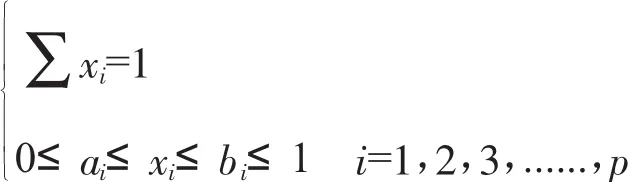

图3 三线坐标图
p个组分,考察区域点集,TP(a,b)非空(即存在符合要求的配方)的充分必要条件为:
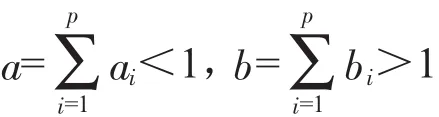
由于混料组分的上、下限约束可能带有多余的约束,令:

用修改后的(ai,bi)来定义TP(a,b)和原区域是等价的,排除多余约束后更为精确。需要说明的是a=∑ai<1,下限之和越小,可以考察的空间越大;b=∑bi>1,上限之和越大,可考察空间越大。在混料设计应用时,按专业知识、经验给出的上下限约束要慎重,与数学方法修改的约束可能存在差异,免得过度压缩考察空间,降低试验设计系统考察的效果。
按上述解除多余约束,得到修改后的(ai,bi)。极端顶点设计中最基本的顶点点集在单形坐标中的位置就被确定。结合本案例,经计算3个分量上下限无多余约束,在三线坐标系上作图为n=5顶点的凸图形。顶点坐标值(x1,x2,x3)和下述计算机计算输出完全一致,限于篇幅不再展开。以此证明,上述解释是合理、正确的。
6 混料回归设计模型
传统的混料设计,数据处理采用全回归模型,也称为混料回归设计。试验设计采用增强方案时需对模型有所了解。
一般回归设计中采用的回归模型是多项式,例如本案例{3,2}一般的三元二次回归方程为:
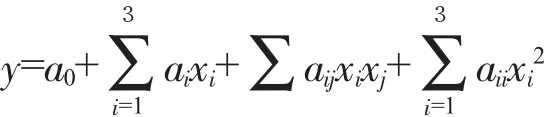
但是混料回归设计不能采用一般的多项式作为回归模型,由于混料条件∑xi=1的限制,会引起信息矩阵的退化,所以需要变换。
由混料条件x1+x2+x3=1可得

代入上式,整理得到混料回归设计中采用的Scheffe多项式形式:
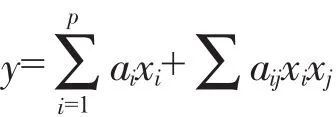
同理可得不完全三次式(d=3),完全三次式(d=3)等。一般三元二次多项式比混料设计{3,2}的Scheffe多项式多了未知的常数项a0及3个二次项系数,也就是说利用混料限制条件∑xi=1,用Scheffe多项式建模,至少可以少做3+1次实验。
d=2时,Scheffe多项式未知项m为:
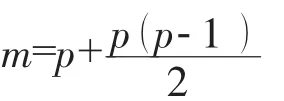
结合本案例{3,2}p=3,m=6。在混料试验设计中考虑到实验误差的影响,以及实验点的均匀性,建议极端顶点设计应采用增强方案,对p个分量,一般要求实验次数 N=(3~5)p。
三、案例极端顶点试验设计方案解构
本案例应用MINITAB软件构建极端顶点实验设计方案。从“统计>DOE(试验设计)>混料>创建混料”入口,显示以下界面:
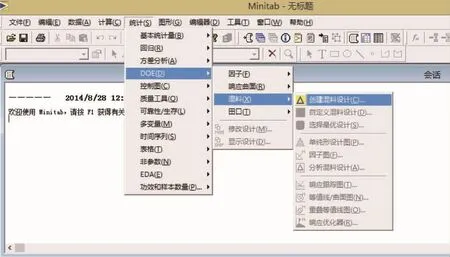
依次点击“极端顶点”,填入分量数“3”,选择设计阶数“2”及“中心点、轴点增强设计”,打开分量窗口,填入单个合计“100”及分量“名称、上下限值”,再打开线性约束窗口,填入分量的“系数,上下限值”,确定后输出本案例的极端顶点试验设计方案。
需要说明的是:
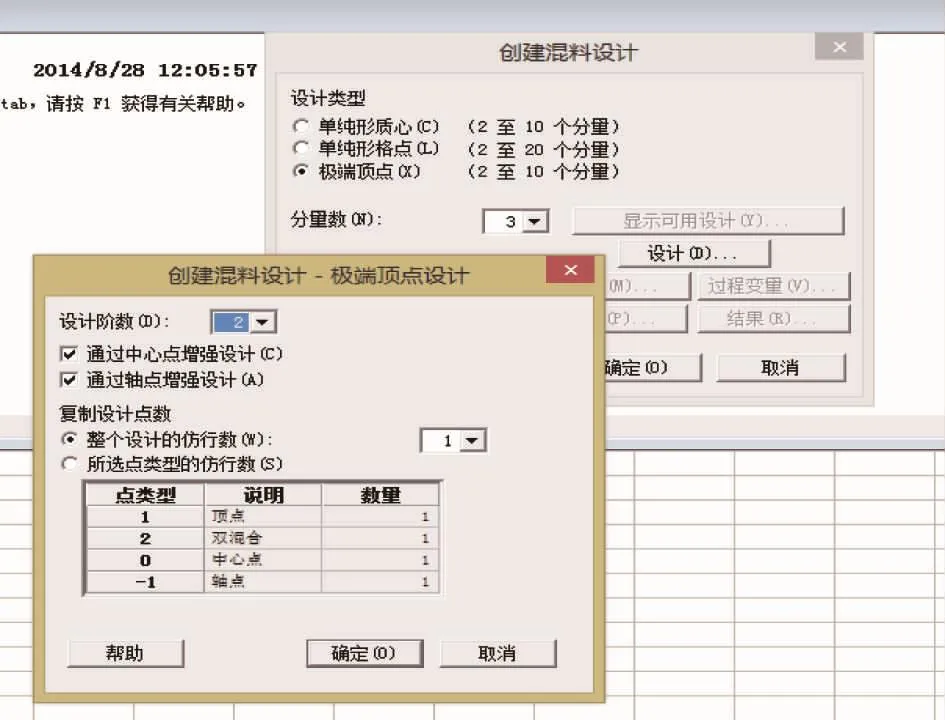

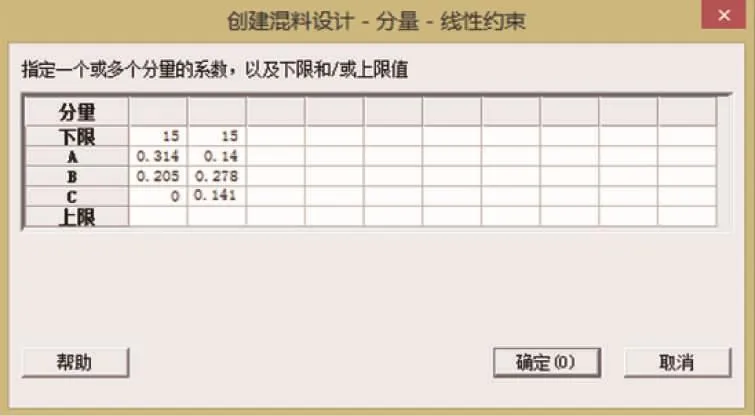
(1)点类型PtType符号1代表顶点;2代表棱线上双混点;3代表d=3棱线上处点;0代表中心点;-1代表轴点。


(2)混料分量的线性约束,是指在各分量上、下限约束的基础上,根据专业知识附加的约束。如本案例膨胀型阻燃剂对总的P,N有附加约束,不能低于15%。根据APP,HACTP,协效剂的分子结构计算可得P,N的含量百分数,构成线性约束。本案例各分量的下限约束已保证附加的线性约束,所以软件MINITAB输出“*”表示可忽略。
(3)软件输出的极端顶点试验设计方案,点集坐标值xi是稳定的,但运行序即实验编号是随机化的。
(4)为了直观了解本案例试验设计方案的布点结构,可以从“统计>DOE>混料>纯形设计图”入口,得到极端顶点设计的布点图。顺时针依次为d=2无增强、中心点增强、轴点增强、双增强布点设计图(见图4)。
四、案例极端顶点试验设计方案计算解析
打开MINITAB软件,选择指令“统计>DOE>混料>分析混料设计”入口后,首先以“LOI”氧指数作为响应填入,然后打开“项”,选定拟合方程的模型分量项为“二次”,再以“可用项”中,按二次Scheffe方程选择所选项“A,B,C,AB,AC,BC”。打开“存储”选择拟合方程中变量项的“系数”及方程的“拟合值”等。

图4 极端顶点设计的布点图
输出本案例极端顶点设计数据处理结果(由图5所示)。
全部增强分析:
混料回归:LOI与 X1,X2,X3
LOI的估计回归系数(分量比率)
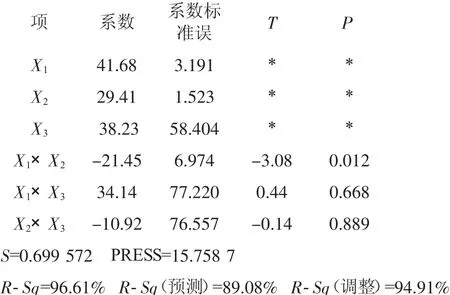
根据计算输出的回归系数,可得Scheffe二次回归方程为:
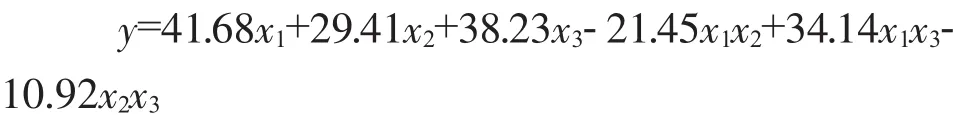
从“统计>DOE>混料>等值线”入口,可得LOI等值线图(见图6)。
对于混料回归设计,传统的方法如本案例对Scheffe二次多项式进行全回归拟合,所以重点分析回归方程的统计指标:
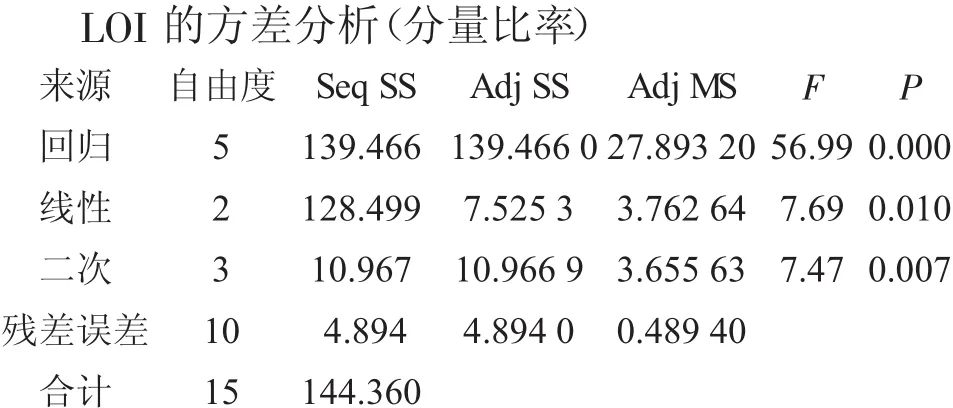
(1)方差分析表明,回归方程及方程中线性项、二次项均高度显著P≤0.01,表明用d=2的Scheffe二次方程拟合是合理的,具有统计意义。
(2)R-Sq和 R-Sq(调整)=94.91%比较接近,且大于由α=0.01,自由度f=n-α=16-2=14查得的相关系数检验的临界值(R=0.622 6),再次表明回归方程拟合具有统计意义。
(3)拟合标准误差S=0.699 6,如用变异系数CV=S/yLol<2%度量,表明具有工程意义。
(4)对回归方程中变量项进行分析,主效应线性项由于受∑xi=1约束,主效应各分项均显著。二次项尽管总体显著,但x1x3,x2x3均不显著,可见模型尚有过度拟合之嫌,尚有改进的空间。
(5)需要指出的是,MINITAB软件在“分析混料设计”时,对线性项、二次项、三次项分别进行方差分析,为应用者对模型的选择、改进提供有效的信息。
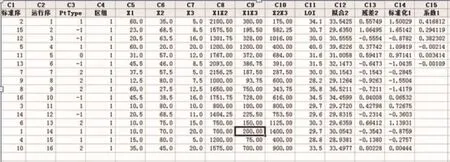
图5 极端顶点设计数据处理结果
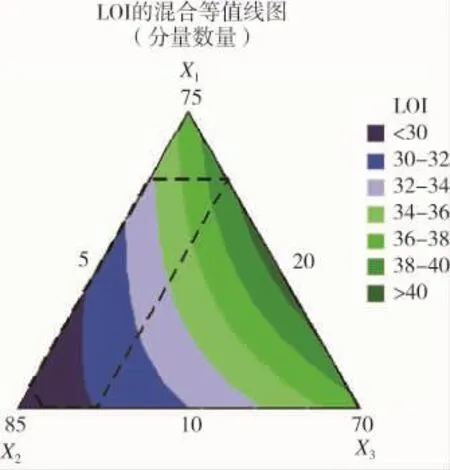
图6 LOI等值线图
(6)统计量PRESS=15.758 7是采用“留一法”形成的残差平方和,对模型预报功能作出整体误差估计,相对应的统计量R-Sq(预测)=89.08%,也大于相应的相关系数临界值,表明模型的预报功能也显著地具有统计意义。
(7)由于混料设计∑xi=1的约束,混料各分量不独立,所以寻找“好点”的方向需在单纯形三线坐标系中“混合等值线”图上进行,由图可见,LOI优化区域在考察范围的右上角,通过调整3个分量的上、下限值可以进一步扩大优化搜索空间。
对于本案例,许肖丽硕士还进行了DPS软件比对计算,结果基本一致。按笔者工作摘记,自8月份以来到定稿,许肖丽和笔者讨论、计算达7次之多。陈涛硕士是首先把极端顶点设计法引入上海化工研究院的。在经典的混料回归设计基础上,现在已发展形成新的混料均匀设计,采用逐步回归法建模,在考察混料配方的同时,还可以考察配方添加量、工艺过程参数及定性因素等新的试验设计方法,扩大了应用范围,提高试验设计效率。但限于篇幅,将另行专题讨论。
本文定稿于2014年国庆期间,混料回归设计是试验设计领域中的新天地,和同仁们共享。
