考虑应力敏感的稠油热采试井模型研究

刘文涛，张德富，程宏杰，王晓光，冯国庆，赵玉龙

(1.新疆油田公司 勘探开发研究院，新疆 克拉玛依 834000； 2.西南石油大学 石油与天然气工程学院，四川 成都 610500)

引 言

试井分析对于油气藏动态监测和地层参数求取具有重要的作用，国内外许多学者对试井解释模型已经做了大量的研究，并绘制出了样板曲线。针对非牛顿幂律流体的试井模型研究，国外学者Ikoku、Ramey等[1-2]研究了多孔介质中非牛顿幂律流体不稳定渗流特征；Vongvuthipornchai[3]在此基础上进一步考虑了井筒储集和表皮效应的影响，求得了均质无限大地层拉氏空间解析解；国内学者栾志安[4]、宋考平[5,6]、梁光跃[7]、李元媛[8]、郭辉[9]、程时清[10]、贾智淳[11]等人对幂律流体的试井解释做了大量的研究。针对考虑应力敏感影响的试井解释模型研究，国外学者Raghavan、Scorerd[12]等人比较完整地描述了考虑应力敏感时介质非线性不定常渗流数学模型；Pedrpsa[13]建立考虑应力敏感时无限大边界试井解释数学模型并给出了解析解；国内学者廖新维[14]、宁正福[15]、刘启国[16]、李顺初[17]、王璐[18]等人分别针对考虑应力敏感时试井解释模型做了大量的研究。

稠油油藏埋藏深，岩石结构疏松，胶结强度弱，在开采过程中地层压力衰减快，压实作用对岩石颗粒骨架造成破坏。我国学者刘国勇[19]、杨东东[20]、熊钰[21]等人从实验的角度对压缩系数与压力、孔隙度与渗透率以及渗透率与压力的关系进行了实验研究，验证了稠油热采过程中应力敏感效应的存在。在注蒸汽开采过程中，蒸汽波及区地层原油黏度下降，视为牛顿流体，未被蒸汽波及的区域流体被视为非牛顿幂律流体，形成流体物性不同的双区复合油藏。因此，本文在前人研究的基础上，建立考虑应力敏感影响的牛顿-非牛顿流体双区复合稠油油藏试井解释数学模型，利用拉氏变换和摄动变换得到拉氏空间解析解，再通过Stehfest数值反演绘制井底无因次压力及导数与无因次时间的双对数理论曲线，分析影响试井曲线特征的因素，指导实测试井资料的解释。

1 数学模型的建立与求解

1.1试井模型建立

针对稠油的热采过程，试井模型可抽象为由牛顿流体-非牛顿幂律流体组成的双区复合油藏(图1)。内区为牛顿流体，外区为非牛顿幂律流体，内外区界面半径为r1。其假设条件如下：

(1)井位于地层中心，油层为水平、均质、等厚的无限大地层，流动呈层流；

(2)各区内流体均为单相微可压缩的液体，忽略重力和毛管力的影响；

(3)各区内流体均符合达西平面径向渗流规律，等温渗流；

(4)考虑井筒储存效应、表皮效应以及应力敏感效应的影响；

(5)两相邻渗流区域界面不存在附加压力降；

(6)非牛顿流体黏度服从Ostwald-De Waele幂律流体模型。根据文献[3]，幂律流体的视黏度与特征黏度的比值可以用内区半径和幂律指数表示，即

(1)

(7)储层渗透率[22]变化关系表示为

K=Kje-γ(pe-p)。

(2)

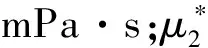
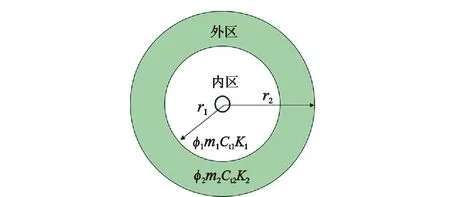
图1 双区复合油藏模型示意图Fig.1 Two-zone composite reservoir model

基于上述假设条件，建立考虑井筒储集效应、表皮效应以及应力敏感效应影响的牛顿-非牛顿流体双区复合油藏试井解释数学模型：

其中无因次参数定义如下：

其中：B为地层原油体积系数，m3/m3；p1、p2分别为内、外区压力，MPa；C为井储系数，m3/MPa；Ct1、Ct2分别为内、外区综合压缩系数，MPa-1；h为有效地层厚度，m；r1为内区半径，m；rw为井筒半径，m；Q为生产井地面产量，m3/d；K1、K2分别为内、外区地层渗透率，μm2；t为生产时间，h；φ1、φ2分别为内、外区地层孔隙度；M12为内外区流体流度之比；η12为内外区储层导压系数之比；S为表皮系数；μ1、μ2分别为内、外区界面处流体黏度，mPa·s；γD为无因次应力敏感系数；rD1为无因次内区半径；pD1、pD2分别为内、外区无因次压力；pwD为无因次井底压力；CD为无因次井储系数；tD为无因次生产时间。

当n=1时，模型(3)退化为常规牛顿流体的双区复合油藏模型。当γD=0时，模型(3)退化为不考虑应力敏感效应的双区复合油藏模型。

1.2 数学模型求解

对方程(3)采用Laplace变换得到拉氏空间方程组，再利用摄动变换取其零阶解得到拉氏空间解析解。摄动变换如下：

只考虑零阶摄动解，则方程(3)通过上述变换之后得到内区与外区微分方程的通解为

(4)

(5)

式中：z为拉普拉斯变量；I0(x)、I1(x)分别为零阶和一阶的第一类修正贝塞尔函数；K0(x)、K1(x)分别为零阶和一阶的第二类修正贝塞尔函数；Kv(x)、Iv(x)分别为v阶的第二类和第一类修正贝塞尔函数。

将式(4)、(5)代入界面连续条件和内边界条件得矩阵方程

(6)

式中：

a34=-1;

a44=CDz;

a14=a24=a33=a43=0。

(7)

2 曲线特征分析与敏感性分析

利用克莱姆法则求解式(6)，再利用stehfest[23]数值反演算法编程求解式(7)，即可得到井底无因次压力和压力导数与无因次时间的双对数关系曲线。

图2为牛顿-非牛顿流体双区复合油藏试井模型典型曲线。根据导数曲线特征，可划分为5个流动阶段：①为井筒储集效应阶段，该阶段无因次压力与压力导数曲线重合，呈一条斜率为1的直线。②为井储向径向流过渡阶段，该阶段无因次压力导数曲线呈现出一个“驼峰”，“驼峰”的高低与表皮系数大小有关。③为内区牛顿流体径向流阶段，受应力敏感的影响，内区无因次压力导数曲线稍有“上翘”，不考虑应力敏感影响时该阶段压力导数曲线为水平的0.5线。④为内区牛顿流体与外区非牛顿流体的过渡流阶段。⑤为外区径向流阶段，描述压力波传播到外区后，内外区流体流动的共同特征。不考虑应力敏感影响时，外区径向流阶段无因次压力导数曲线呈斜率为(1-n)/(3-n)的直线；考虑应力敏感影响时，其特征表现为无因次压力导数曲线“上翘”幅度更大且高于(1-n)/(3-n)斜率直线。随着时间的推移，压力波不断向外传播，围绕井筒形成的压降漏斗不断扩大、不断加深，从而导致内外区渗透率由于应力敏感影响形成的渗透率漏斗也不断扩大、不断加深，即压降漏斗内的平均渗透率随时间降得更低，呈现出晚期比早期更明显的应力敏感效应。

图2 牛顿-非牛顿双区复合油藏试井模型典型曲线Fig.2 Typical well-test curves of Newtonian-non-Newtonian composite reservoir model

图3为幂律指数对井底压力动态的影响关系曲线。实线代表不考虑应力敏感时无因次压力和压力导数的变化曲线，虚线代表考虑应力敏感时无因次压力和压力导数的变化曲线。由于外区为非牛顿幂律流体，当不考虑应力敏感时，外区无因次压力导数曲线呈斜率为(1-n)/(3-n)的直线，幂律指数越小，直线斜率越大；当考虑应力敏感时，外区的无因次压力导数曲线呈高于(1-n)/(3-n)斜率直线的“上翘”曲线，幂律指数越小，曲线“上翘”越明显。应力敏感效应和非牛顿幂律流体都会使得压力和压力导数曲线上翘，所不同的是：非牛顿幂律流体作用下压力导数呈一定斜率的直线，而应力敏感影响下的压力导数曲线上翘但不成一定斜率的直线。在对实际资料进行解释时，可根据幂律流体黏度测定或储层岩心应力敏感实验先初步确定幂律指数或应力敏感系数，再进行解释，从而降低实测试井资料解释的多解性。

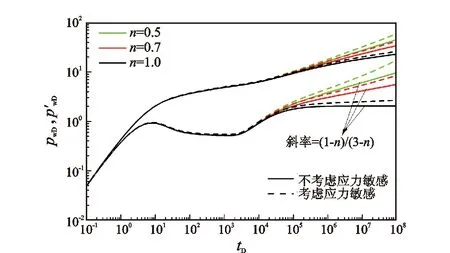
图3 幂律指数对井底压力动态影响关系曲线Fig.3 Influence of power law index on bottom-hole dynamic pressure

图4为内区与外区界面流度比对井底压力动态的影响关系曲线。当不考虑应力敏感时，流度比越小，外区径向流阶段无因次压力导数曲线呈斜率为(1-n)/(3-n)斜线的位置越低；考虑应力敏感时，其无因次压力导数曲线特征有着类似的变化特征，流度比越大，导数曲线偏离(1-n)/(3-n)斜率直线的时间越早，偏离程度越大。

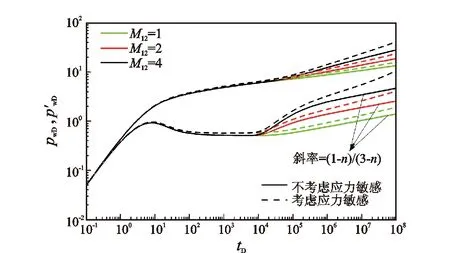
图4 内区与外区界面流度比对井底压力动态影响关系曲线Fig.4 Influence of mobility ratio at the interface between inner zone and outer zone on bottom-hole dynamic pressure

图5为内区半径对井底压力动态的影响关系曲线。内区半径的大小主要影响内区径向流阶段持续的时间和外区径向流阶段的开始时间。内区半径越小，内区径向流阶段持续时间越短，无因次压力导数曲线中0.5水平线越短。考虑渗透率应力敏感效应时，外区径向流阶段压力导数曲线位置越高，外区径向流阶段压力导数曲线“上翘”越明显。

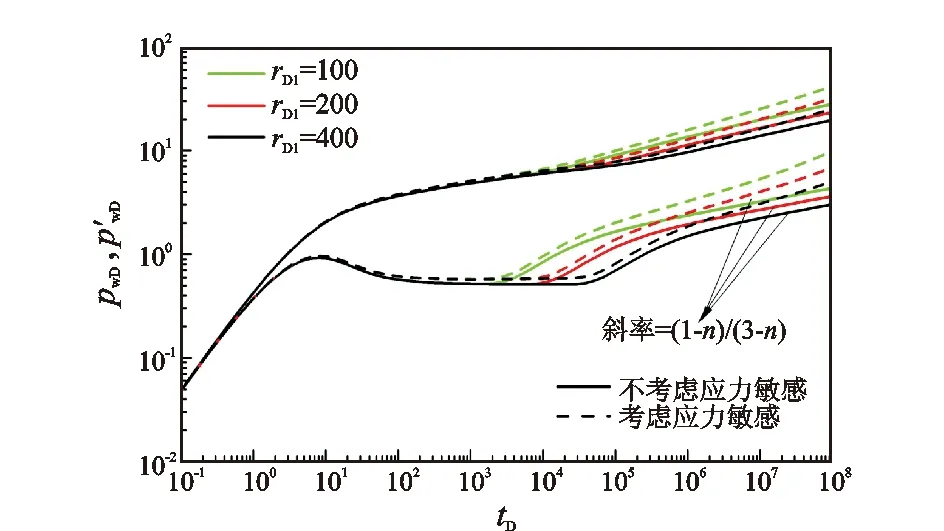
图5 内区半径对井底压力动态影响关系曲线Fig.5 Influence of inner zone radius on bottom-hole dynamic pressure

3 结 论

(1)应力敏感效应显著影响牛顿-非牛顿流体双区复合油藏试井模型曲线的变化。存在应力敏感效应影响时外区径向流阶段压力导数曲线上翘且高于(1-n)/(3-n)斜率直线。

(2)幂律指数越小，外区径向流阶段压力导数曲线“斜率”越大。应力敏感系数越大，外区径向流阶段压力导数曲线“上翘”越明显。

(3)内、外区的流度比越大，外区径向流阶段压力导数曲线越高；内区半径越小，内区径向流持续时间越短。

参 考 文 献：

[1] IKOKU C U,RAMEY H J.Wellbore storage and skin effects during the transient flow of non-newtonian power-law fluids in porous media[C].SPE 7449-PA,1980.

[2] IKOKU C U,RAMEY H J.Transient flow of non-newtonian power-law fluids in porous media[C].SPE 7139-PA,1979.

[3] VONGVUTHIPORNCHA S,RAGHAVAN R.Well test analysis of data dominated by storage and skin:non-newtonian power-law fluids[C].SPE 14454-PA,1987.

[4] 栾志安.双重介质非牛顿液不稳定渗流解析解[J].石油学报,1981,2(4):75-79.

LUAN Zhian.Analytical solution of unsteady seepage flow in non-newtonian fluid[J].Acta Petrolei Sinica,1981,2(4):75-79.

[5] 宋考平,王雷,计秉玉.非牛顿-牛顿复合油藏渗流试井解释方法[J].石油学报,1996,17(1):82-86.

SONG Kaoping,WANG Lei,JI Bingyu.Well test analysis of a compound reservoir with non-Newtonian and Newtonian fluid flow[J].Acta Petrolei Sinica,1996,17(1):82-86.

[6] 宋考平,祝俊峰,刘泽俊,等.多区复合油藏非牛顿幂律流体试井解释[J].石油学报,1997,18(2):78-83.

SONG Kaoping,ZHU Junfeng,LIU Zejun,et al.Well test analysis for a compound reservoir with non-newtonian power law fluids flow[J].Acta Petrolei Sinica,1997,18(2):78-83.

[7] 梁光跃,廖新维,万光芬,等.非牛顿幂律流体试井模型的有效半径解及其曲线特征[J].科技导报,2010,28(13):58-61.

LIANG Guangyue,LIAO Xinwei,WAN Guangfen,et al.Effective wellbore radius and typical curve characteristics of well test analysis of non-newtonian power-law fluids[J].Science & Technology Review,2010,28(13):58-61.

[8] 李元媛,蔡睿贤.非牛顿幂律流体试井模型的一种简明解析解[J].科技导报,2010,28(18):32-35.

LI Yuanyuan,CAI Ruixian.A concise analytical solutions of well test analysis:non-newtonian power-law fluids[J].Science & Technology Review,2010,28(18):32-35.

[9] 郭辉,程时清,于海洋,等.聚合物驱复合模型试井分析方法[J].断块油气田,2014,21(4):504-508.

GUO Hui,CHENG Shiqing,YU Haiyang,et al.Well test analysis method of composite model by polymer flooding[J].Fault-Block Oil & Gas Field,2014,21(4):504-508.

[10] 程时清,聂向荣.聚合物驱复合油藏试井模型与典型曲线[J].华中科技大学学报(自然科学版),2012,40(4):110-113.

CHENG Shiqing,NIE Xiangrong.Well test model and type curives of composite reservoirs with polymer flooding[J].Hua Zhong University of Science & Technology(Natural Science Edition),2012,40(4):110-113.

[11] 贾智淳,闫术,董晓芳,等.剪切变稀作用对聚驱试井分析影响的数值研究[J].西南石油大学学报(自然科学版),2016,38(5):108-113.

JIA Zhichun,YAN Shu,DONG Xiaofang,et al.Numerical study on the impact of shear thinning behavior in well test analysis for polymer flooding[J].Journal of Southwest Petroleum University (Science & Tecnology Edition),2016,38(5):108-113.

[12] RAGHAVAN R,SCORER J D T,MILLIER F G.An investigation by numerical methods of the effect of pressure-dependent rock and fluid properties on well flow tests[C].SPE 2617-PA,1972.

[13] PEDROSA O A.Pressure transient response in stress-sensitive formations[C].SPE 15115,1986.

[14] 廖新维,冯积累.超高压低渗气藏应力敏感试井模型研究[J].天然气工业,2005,25(2):110-112.

LIAO Xinwei,FENG Jilei.Well test model of stress sensitive gas reservoirs with super high pressure and low permeability[J].Natural Gas Industry,2005,25(2):110-112.

[15] 宁正福,廖新维,高旺来,等.应力敏感裂缝性双区复合气藏压力动态特征[J].大庆石油学院学报,2004,28(2):34-36.

NING Zhengfu,LIAO Xinwei,GAO Wanglai,et al.Pressure transient response in deep-seated geothermal stress-sensitive fissured composite gas reservoir[J].Journal of Daqing Petroleum Institute,2004,28(2):34-36.

[16] 刘启国,唐伏平,冯国庆,等.开关井不同程度应力敏感效应对井底压力动态的影响[J].石油与天然气地质,2007,28(4):523-525.

LIU Qiguo,TANG Fuping,FENG Guoqing,et al.Influence of different stress sensitivities on bottom hole pressure behaviors during well opening and shut-in[J].Oil & Gas Geology,2007,28(4):523-525.

[17] 李顺初,任丽,郑鹏社,等.基于应力敏感的天然裂缝性页岩气藏双孔模型解的结构[J].应用数学和力学,2017,38(2):233-242.

LI Shunchu,REN Li,ZHENG Pengshe,et al.Similar structure of the solution to the dual-porosity model for naturally fractured shale gas reservoirs based on stress sensitivity[J].Applied Mathematics and Mechanics,2017,38(2):233-242.

[18] 王璐,姚约东,黄山,等.裂缝性致密油藏非稳态窜流规律[J].断块油气田,2016,23(3):329-333.

WANG Lu,YAO Yuedong,HUANG Shan,et al.Transient cross flow law for fractured tight oil reservoirs[J].Fault-Block Oil & Gas Field,2016,23(3):329-333.

[19] 刘国勇,刘阳,张刘平.压实作用对砂岩储层物性的影响[J].西安石油大学学报(自然科学版),2006,21(4):24-28.

LIU Guoyong,LIU Yang,ZHANG Liuping.Experimental study on the effects of compaction on the properties of sandstone reservoir[J].Journal of Xi’an Shiyou University(Natural Science Edition),2006,21(4):24-28.

[20] 杨东东,戴卫华,张迎春,等.渤海砂岩油田岩石压缩系数经验公式研究[J].中国海上油气,2010,22(5):317-319.

YANG Dongdong,DAI Weihua,ZHANG Yingchun,et al.Studying on an empirical formula of rock compressibility for sandstone oilfields in Bohai sea[J].China Offshore Oil and Gas,2010,22(5):317-319.

[21] 熊钰,李航,耿站立,等.压实与出砂双重作用下疏松砂岩稠油油藏产能变化实验[J].中国海上油气,2015,27(6):63-68.

XIONG Yu,LI Hang,GENG Zhanli,et al.Experimental study on productivity change of unconsolidated standstone heavy oil reservoir under the dual effect of compaction and sand production[J].China Offshore Oil and Gas,2015,27(6):63-68.

[22] RAGHAVAN R,CHIN L Y.Productivity changes in reservoirs with stress-dependent permeability[C].SPE 77535,2002.

[23] STEHFEST H.Numercial inversion of laplace transform[J].Communication of ACM,1970,13:47-49.