肘形流道进口断面敏感性分析

王自明，刘 云，王月华

（浙江省水利河口研究院，浙江 杭州 310020）

1 问题的提出

随着城镇内涝问题日益突出，为了有效缓解内涝隐患，“强排”“扩排”成为效益突出、见效最快的解决措施，泵站也成为引水排涝的首选措施。但由于大部分工程隶属改建、扩建项目，建设条件较为复杂，也再次推动了泵站选型及结构优化等科研工作。

目前，由于成本低、周期短，泵装置研究工作较多地采用CFD（计算流体动力学）技术，如陆林广等对簸箕型[1-2]、钟型[3]、肘型[4-5]及双向[6-8]泵装置进水流道的水力特性研究，并将数值计算与物模试验进行对比，得到与试验数据较为吻合的结果；成立、朱荣生等对泵站出水流道[9-10]的水头损失及体型优化进行数值计算；陆林广对进水流道的基本流态及优化设计成果进行详细的分析[11-12]；朱红耕对泵站进口高度的水力特性进行研究[13]。但研究主要集中于流道的优化及水力特性研究，而流道进口断面各参数对流道水力特性的敏感性方面一直缺乏深入研究。

本文采用CFD技术，对典型泵站的进水流道进行数值模拟，在流道长度L和水泵叶轮直径D保持不变的情况下，通过对肘形流道不同宽度、高度以及进口面积的敏感性进行分析，从而得到较为合理的肘形流道进口断面体型，也为类似工程提供依据。

2 工程概况

工程位于某河道支流口门，主要功能为降低下游防洪压力，将涝水排入外江。泵站设5台立式轴流泵，单泵流量33 m3/s，每台泵进口流道为1孔，采用肘形进水流道，孔口尺寸5.40 m×7.50 m（高×宽），进水前池底板高程-6.30 m，泵站最低运行水位3.00 m，其中流道长度L为11.30 m，流道进口宽度B为7.50 m，高度H为5.40 m，水泵叶轮直径D为3.00 m，排水泵站的平面及剖面见图1。

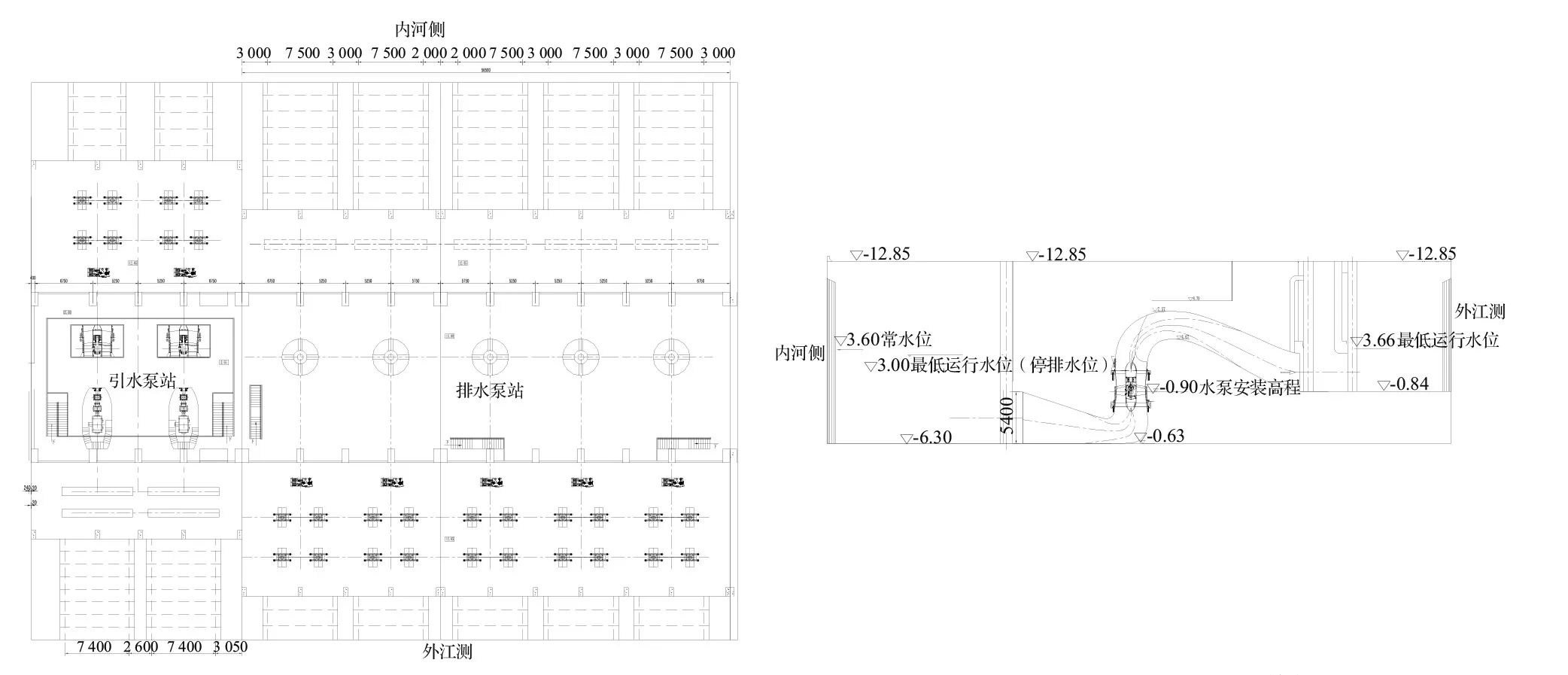
图1 排水泵站平面及剖面图 单位：mm

3 CFD模型建立

3.1 控制方程

计算采用了RNG k - ε模型，分别引入反映湍流动能（k）方程和反映湍流耗散率（ε）方程，并假设流道内为无热量交换的不可压缩流动，控制方程由连续性方程和动量方程组成，具体如下：

式中：u为速度矢量（m/s）；p为密度（kg/m3）；t为时间（s）；p 为流体上的压力（Pa）； μ为动力粘度（Pa · s）；fx、fy、fz为单位质量力（m/s2）；u、v、w为速度在x、y、z方向的分量（m/s）。

3.2 计算区域及边界条件

流道计算区域由前池、进水流道和出水直管3部分组成，其中流道采用非结构网格，进水池及出水直管采用结构网格。前池进口采用速度进口边界条件，前池的表面作对称平面处理。出口采用自由出流边界，为保证进水流道出口为充分发展的流动，将进水流道出口断面沿断面法向等直径延长2倍圆管直径。此外前池底、进水流道边壁边界条件按固壁定律处理。泵装置进水流道的流场计算区域及网格剖分见图2。

图2 进水流道流场计算区域网格示意图

4 敏感性分析

4.1 敏感性分析指标

为研究肘形流道进口断面高度及宽度的敏感性，通过流速分布均匀度、流速加权平均角度及进水流道水头损失3个指标作为目标函数，分别考察流道出口处流速的分布情况及流速的偏转角度以及流道的水头损失。

4.1.1 流速分布均匀度

流速分布均匀度计算公式为：

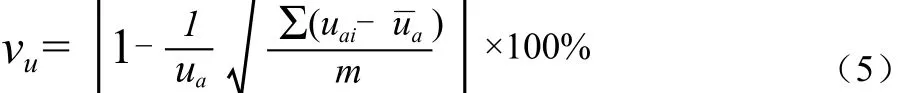
式中：ua为出口断面的平均轴向流速（m/s）；uai为出口断面第i个单元的轴向流速（m/s），m为流场数值计算时该断面所划分的网格单元数（个）。

4.1.2 流速加权平均角度

在姜黄切片、粉末的颜色值测定中发现，同一样品任取的切片，10个颜色值之间差异较大，RSD值均大于15%；同一样品粉末（混匀过4号筛），颜色值之间差异较小，RSD值均小于5%。表明采用姜黄粉末得到的颜色值精密度较高；进而选取粉末颜色值与姜黄素类各成分含量的相关关系作为本研究的实验结果。因此，通过颜色值预测药材品质的快速鉴别方法，应采用粉末的颜色值进行判定较为适宜。

流速加权平均角度计算公式为：

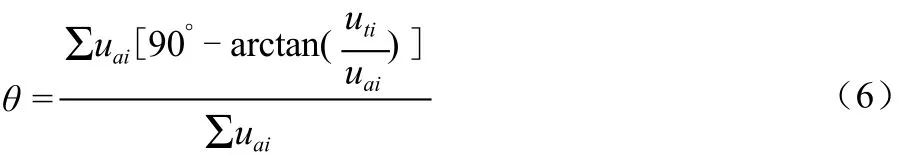
式中： uti为进水流道出口断面i单元的横向速度（m/s）。

4.1.3 水头损失

水头损失为流道进口断面与出口断面的水头差（m）。

4.2 计算方案

为分析泵站进水流道几何尺寸变化对流速均匀度、流速加权平均角度及水头损失的敏感性，分别改变肘形流道进口断面宽B、高H，连同原方案在内共计算了10组方案。方案中流道长度及叶轮半径固定不变，其他参数的取值范围参照泵站设计规范即B/D在2.00 ～ 2.50范围内、H/D在1.50 ～ 2.20范围内。原方案中L = 11.30 m，B = 7.50 m，H = 5.40 m，D = 3.00 m，其中L/D = 3.77、B/D = 2.50、H/D = 1.80。不同计算方案参数取值范围见表1。

表1 流道计算各方案参数取值范围表

4.3 敏感性分析

4.3.1 流速均匀度

对各方案的流速均匀度进行计算，其结果见图3。进水流道高度不变时，流速均匀度随着进水流道的宽度的增大而增大；当宽度不变时，流速均匀度出口断面轴向流速分布均匀度总体上随着H/D的增大而略有减小。但是各方案的出口断面轴向流速分布均匀度相差不大，最大时只差1.38%。说明流道进口高度及宽度的变化对于流速均匀度为次要敏感参数。

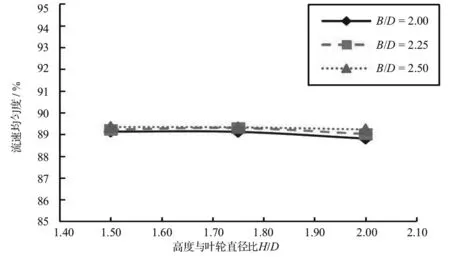
图3 流速均匀度图

各方案流速加权角度计算结果见图4。在9组计算方案中流速加权平均角度的值基本在89.57°左右，最大时差0.01 s，变化较小。说明流道进口高度及宽度的变化对流速加权平均角度为次要敏感参数。

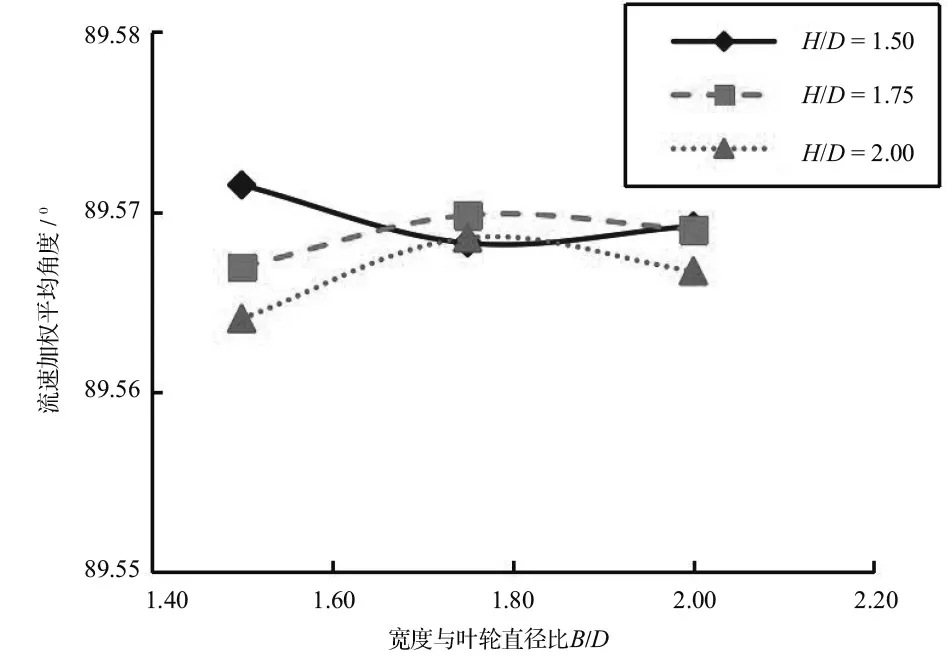
图4 流速加权角度图

4.3.3 水头损失

各方案的水头损失见图5。当进水流道长度固定，水头损失随着流道高度和宽度的增大而减小，最大水头损失可达0.15 m，其对泵装置水力性能的影响已不可忽略。水头损失与高度及宽度均呈单调递减关系，为主要敏感参数。

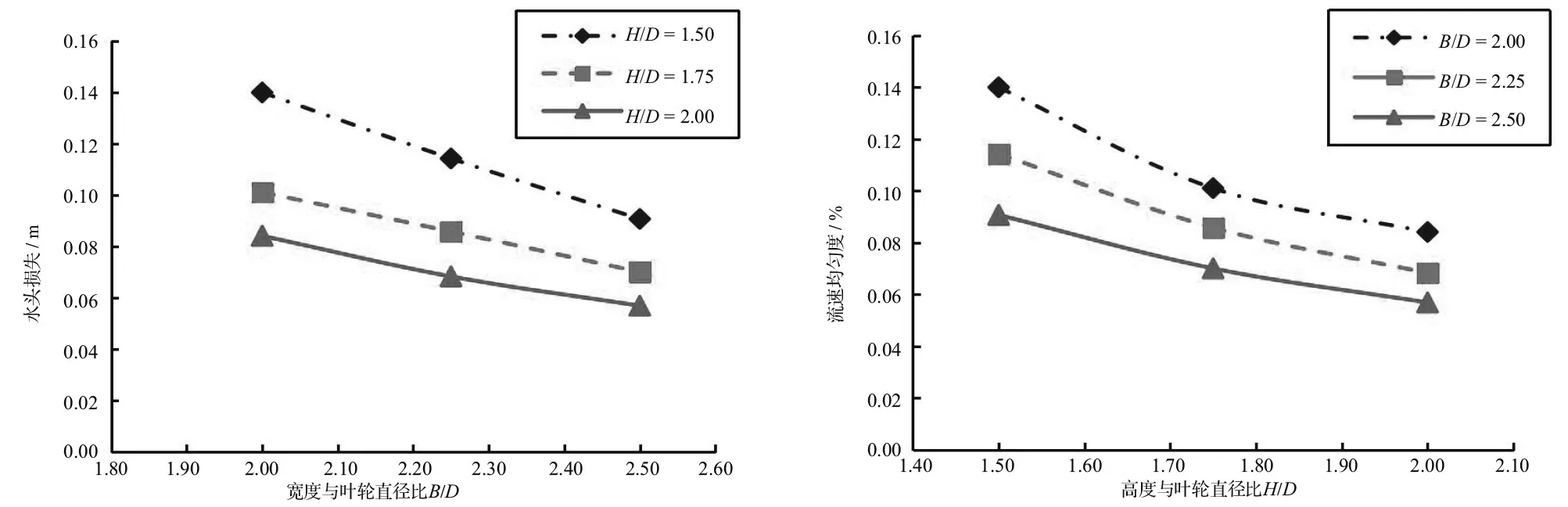
图5 B、H变化时水头损失变化图

4.4 综合分析

为进一步研究高度和宽度的变化对水头损失的影响，引入能够反映断面宽度和高度变化的综合参数即进口断面面积。

图6 a为肘形流道进水口的面积与水头损失的关系图。从图6 a中可以得出当肘形进水流道进口的面积越大其水力损失越小。

为了进一步研究进口断面增幅与水头损失降幅的相关性，以断面面积最小方案即方案1为参照，分析各方案增加单位进口断面面积时水头损失的减小量。结果表明，随着断面面积的不断增大，泵站沿程的水头损失减小量存在极值，其分布呈类似高斯分布[见图6 b]。其中当断面面积增加了4.5 m2时，单位面积水头损失降幅最大，随后呈逐渐下降趋势，即存在最优经济解。因此综合考虑成本、水头损失、流速均匀度及流速加权平均角度等因素选择方案4（即H/D = 1.75，B/D = 2.00）为最佳方案。

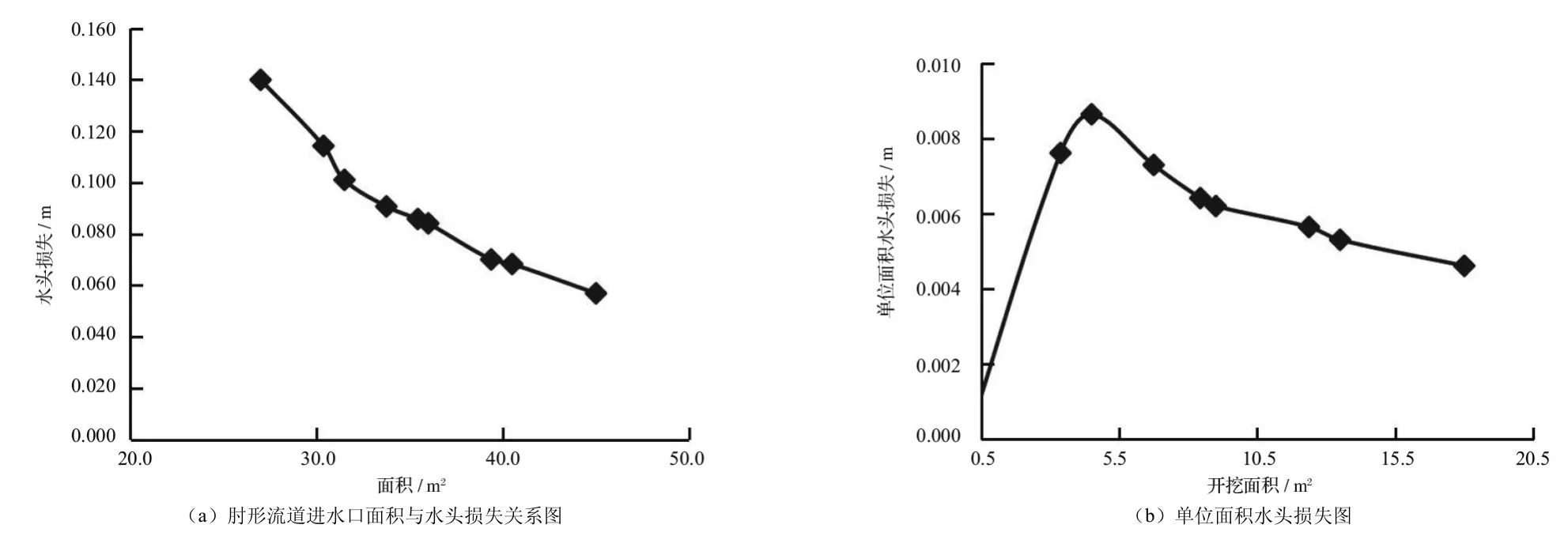
图6 水头损失变化与断面面积的关系图

5 结 语

通过CFD计算，对泵站肘形进水流道尺寸开展敏感性分析，重点分析流速分布均匀度、流速加权平均角度及进水流道的水头损失3个指标。结果表明，在相同的L/D条件下，流道进口尺寸高度及宽度的变化对于流速分布均匀度及流速加权平均角度为次要敏感参数，而对于水头损失为主要敏感参数，且呈递减函数。进一步研究表明，随着进口断面面积的增大，水头损失的减小量存在极值，即存在最优经济解。因此在方案比选的过程中，可忽略高度及宽度对流速分布均匀度及流速加权平均角度的影响而直接考虑断面面积对肘形流道水头损失的影响。该成果可为类似泵站的流道设计及优化工作提供借鉴。

参考文献：

[1] 陆林广，周济人，叶健，等.簸箕形进水流道的优化水力设计[J].水利学报，1997(9)：32 - 37.

[2] 成立，刘超，周济人，等.大型立式泵站簸箕型进水流道三维紊流数值模拟[J].水力发电学报，2004(4)：65 - 68.

[3] 何钟宁.大型泵站钟形进水流道三维数值模拟与试验研究[D].扬州：扬州大学，2007 .

[4] 刘为民.泵站进水流道对水泵性能影响的数值模拟研究[D].扬州：扬州大学，2005.

[5] 杨应玖.大型立式轴流泵站肘形进水流道的设计[J].排灌机械，1984(1)：12 - 16.

[6] 成立，刘超，周济人，等.大型立式泵站双向进水流道三维紊流数值模拟[J].农业机械学报，2004(3)：61 - 64.

[7] 郭绍艾.潜水泵站方箱式双向进水流道设计[J].河北水利水电技术，2003(2)：3 - 4.

[8] 陆林广，张仁田.方箱式双向进水流道的优化水力设计[J].水利水运科学研究，1997(1)：73 - 81.

[9] 成立，刘超，周济人，等.基于RNG湍流模型的双向泵站出水流道流动计算[J].水科学进展，2004(1)：109 - 112.

[10] 朱荣生，李维斌，黄道见，等.泵站出水流道的数模分析[J].农机化研究，2003(3)：79 - 80，84.

[11] 陆林广.泵站进水流道设计.河海大学学报[J].2001，29(1)：40 - 45.

[12] Lu lin guang.Basic flow patterns and optimum hydraulic design of a suction box of pumping station[J].Journal of Hydrodynamics，2000(4)：46 - 51.

[13] 朱红耕.H_D值对肘形进水流道水力特性影响的数值模拟[J].水利与建筑工程学报，2004，2(4)：8 - 10.