基于极化-空间谱特征的雷达目标检测方法

， ， ，

(1. 国防科技大学电子信息系统复杂电磁环境效应国家重点实验室， 湖南长沙 410073；2. 武汉滨湖电子有限责任公司， 湖北武汉 430000)

0 引言

雷达面临的主瓣压制干扰(简称“主瓣干扰”)威胁不断增大，有意干扰方面，伴随式电子干扰在防空反导突防作战中愈发重要；无意干扰方面，同频段民用射频干扰无处不在，对临近方向的雷达目标形成了强烈压制。由于主瓣干扰具有雷达接收增益大的主要特点，且雷达无法采用波束置零等空域手段抑制，因而已成为雷达探测面临的重要挑战。

极化是描述电磁波矢量特征的基本参量，雷达极化域抗干扰技术近年来得到了迅速的发展，已在压制干扰抑制、欺骗干扰鉴别等方面获得了诸多成功应用，其中最为典型的应用就是通过极化滤波手段抑制主瓣压制干扰。早在1975年，美国佐治亚理工学院的Nathanson教授就提出自适应极化对消器(APC)用于对消雨杂波[1]，Giuli，Gherardelli等在此基础上提出了多凹口自适应极化对消器(MLP-APC)[2]、多凹口次最优自适应极化对消器(MLP-SAPC)[3]的概念，此后APC进一步又被用于抑制宽带阻塞干扰等主瓣干扰。国内方面，多家单位研究了极化滤波抗干扰问题，包括国防科学技术大学、哈尔滨工业大学、空军雷达学院、空军装备研究院等单位。施龙飞等提出了APC加权系数的数字迭代计算方法[4]，任博等设计了基于极化聚类中心的自适应极化滤波器[5]，能够快速估计干扰信号极化状态实现当前脉冲周期内的极化滤波，此外，毛兴鹏等研究了基于斜投影算子的极化滤波器等[6]。

由于仅通过极化域滤波对干扰的抑制能力是有限的，极化抗干扰技术逐渐从单一极化域处理向多域联合处理发展，但更多的仍然是干扰功率抑制、信干噪比提升方面。Showman等提出在空-时自适应处理(STAP)之后串联一个极化匹配滤波器或极化白化滤波器，用来改善杂波/干扰背景下的目标检测，称之为极化-空-时自适应处理(PSTAP)[7]。Fante等提出利用N个双极化天线进行极化-空-时域的联合处理能够对消2N-1个干扰[8]。国内，哈尔滨工业大学、电子科技大学、国防科学技术大学等单位均研究了极化与空、时域联合处理的问题，其中，毛兴鹏等研究了极化域-频域联合滤波[9]，吴迪军在机载相控阵雷达空-时-极化域自适应处理方面开展了研究工作[10]，施龙飞等研究了基于双极化主辅阵列的主瓣、旁瓣干扰联合对消技术[11]。

然而，极化滤波效果主要依赖于信号的极化度，对于主瓣内存在多点源干扰情况(多个独立干扰源)或变极化干扰的情况，由于(合成)信号极化度较低，导致上述极化滤波以及联合域滤波方法性能均严重下降。通过抑制干扰功率、提升信干噪比(Signal Interference Noise Ratio, SINR)实现目标检测的传统技术路线对于主瓣多点源干扰、主瓣变极化干扰的情况可能是难以适用的。

对此，本文转而利用有源干扰与雷达目标在极化散射特性响应特征方面的差异，立足于极化阵列雷达和发射极化分集体制，提出一种基于极化-空间联合谱特征的目标检测方法，从特征上鉴别干扰与目标，实现主瓣多点源、变极化干扰背景下的目标检测。本文阐述了该方法的基本原理、实现方法，并对其检测性能进行了初步分析和仿真。

1 基本原理

本文立足于从“特征差异”上区分干扰与目标，将目标和干扰都作为待检信号，并利用“特征”进行确认检测。下面首先分析目标与干扰之间的极化散射特征差异。

设雷达采用一对正交极化天线，不失一般性地，令其为水平(H)和垂直(V)极化天线。雷达采用发射极化分集体制，设发射极化在PRI(Pulse Repetition Interval)间捷变，H，V极化通道同时接收。

文献[12-13]利用雷达目标回波极化随发射极化线性改变、有源干扰极化与发射极化无关的差异，提出了雷达目标与有源假目标干扰的极化鉴别方法。本文将这种差异应用于主瓣多点源压制干扰等场景，提出基于极化-空间联合谱特征的雷达目标检测方法，其思路是：采用极化-空间联合谱估计处理，将不同发射极化对应的极化-空间联合谱进行融合处理，利用目标回波在联合谱上的谱峰角度相同、极化不同而呈现出的“散度”特征与干扰谱峰角度相同、极化相同的“聚集性”进行区分，进而实现对目标的等效检测。

1.1 信号模型

下面首先建立极化-空间联合谱估计处理后的信号模型。

为分析方便，仅考虑一维线阵，典型的双极化均匀线阵如图1所示。设阵列共有K个阵元，每个阵元由一个正交偶极子对构成，设H极化与x轴平行，V极化与x轴垂直、与y轴平行，z轴与x轴、y轴符合右手螺旋准则。

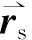
(1)

式中，s(t)为目标回波信号波形。

上述均匀线阵中，第k个阵元接收到的目标回波信号为

(2)

(3)

同理，若共有M个完全极化干扰源，那么对于第m个干扰来说，假设其到达角为(θJm,φJm)，极化相位描述子为(γJm,ηJm)(需指出的是，不同的到达角方向，其极化相位描述子所在的极化坐标系是不同的)，则位于原点处的双极化阵元接收到的干扰信号矢量为

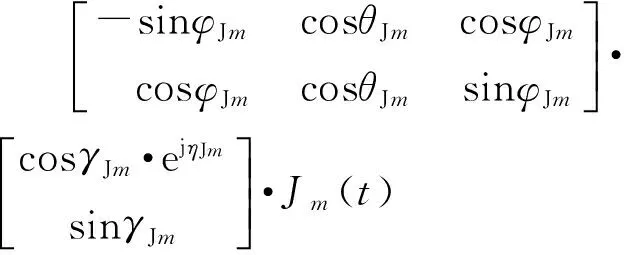
(4)

式中，Jm(t)为第m个干扰信号波形。那么第m个干扰的输出信号拉伸矢量为

(5)

最终可得阵列输出信号矢量:

(6)

式中，N为接收通道噪声，N=[n1(t),n2(t),…,nK(t)]T，nk(t),k=1,2,…,K。

1.2 基本原理

设发射极化分集数为N，对每个发射极化对应接收信号进行极化-空间联合谱估计，得到N个极化-空间联合谱。

若雷达天线主瓣内有1个目标和M个有源干扰，且已知或已正确估计信源个数，则理论上每个联合谱中共有M+1个峰值，在第n张谱上目标和干扰的峰值分别记为(θsn,γsn)，(θJm,γJm)，m=1∶M处。考虑到一个CPI(相干处理时间)内，目标、干扰相对于雷达的方位角和俯仰角变化可以忽略不计，那么，可将N个极化-空间联合谱叠加得到合成谱P(θ,φ,γ,η)：

(7)

式中，Pn(θ,φ,γ,η)为第n组发射极化对应的极化-空间联合谱，n=1,2,…,N，其中θ为俯仰角，φ为方位角，极化角γ，η为极化矢量相位描述子，γ为相对幅度信息，η为相对相位信息。

由于目标极化随发射极化变化，干扰极化固定不变，因此，P(θ,φ,γ,η)共有M+N个峰值点，分别为(θsn,γsn)和(θJm,γJm)(n=1∶N，m=1∶M)，前者为目标对应的N个极化响应峰值，后者为M个干扰对应的峰值。

如图2所示，目标对应的N个峰值具有空间角度相同而极化状态不同的特点，可描述为极化-空间四维复空间上同一空间网格中的“散度特征”，这种散度特征有助于将目标从众多谱峰中检测出来。

2 基于极化-空间联合谱特征的目标检测方法

第1节介绍了基于极化-空间联合谱特征的目标检测原理，并将目标检测问题简化为联合谱图像中同一空间网格中的散度特征检测问题，本节研究目标检测方法。

2.1 检测方法

本文提出一种基于极化-空间谱特征的目标检测方法，其基本流程如图3所示。

1) 对H，V极化接收通道的信号进行极化-空间联合谱估计后，将N个发射极化对应联合谱取模并叠加得到合成谱；

2) 对合成谱进行四维CFAR初检测、空间网格划分；

3) 对每个空间网格中的初检测结果统计其极化特征检测量，并与门限比较，得到确认检测结果。

下面，具体阐述其中的合成谱四维CFAR初检测和确认检测。

1) 四维CFAR初检测

初检测是对合成谱P(θ,φ,γ,η)进行四维CA-CFAR检测和点迹合并，得到疑似目标。

四维CA-CFAR检测方法是一维CA-CFAR检测方法的简单拓展，即在(θ,φ,γ,η)构成的四维空间中，在待检测点周围选择与其在4个坐标轴上均相距若干个分辨单元(即保护单元)的点(即参考单元)，若保护单元数为2，则参考单元数为16个，将参考单元的幅度值进行平均作为背景参考电平。

设经过四维CA-CFAR检测和点迹合并后共有I个疑似目标，记录每个疑似目标在合成谱P(θ,φ,γ,η)上的坐标位置(θi,φi,γi,ηi)，i=1,…,I。

2) 确认检测

确认检测过程是对疑似目标进行进一步的确认，以判定其是否为目标。

在(θ,φ,γ,η)四维空间的俯仰角θ轴和方位角φ轴上，设以0.1°为间隔划分网格(一般取目标或干扰源之间可能的最小角度间隔为网格大小)。计算落入每个网格内的过门限点(θi,φi,γi,ηi)(i=1,…,I)数目，对数目大于或等于N的网格均进行确认检测处理。

(8)

下面阐述如何依据极化比均值和方差，获得检测统计量。

2.2 检测统计量与检测门限

以干扰为对象研究确定检测统计量。

(9)

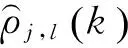
(10)

则有

(11)

(12)

设H1假设为目标，H0假设为干扰，则有

H1:L≥LD

H0:L

(13)

(14)

式中，P，PJ分别为接收信号总功率、干扰信号总功率，则式(10)、式(9)中：

(15)

3 仿真分析

仿真实验设有1个目标和2个干扰，共3个信源，为分析简便，设这3个信源的方位角均为φ=90°、极化角η=0°(即线极化)。目标极化散射矩阵为单位矩阵，俯仰角为0°。干扰信号均为噪声压制干扰，极化状态分别设置为水平极化、45°线极化，俯仰角分别为-1°，1°。

雷达基本参数设置如下：极化敏感阵列共设置8个阵元，正交双极化(H，V)同时接收极化，发射分时极化分集，分集数为4(γt1=0，γt2=π/6，γt3=π/3，γt4=π/2)。

图5(a)为4个发射极化对应极化-空间联合MUSIC谱叠加后形成的合成谱，图5(b)为二维检测后得到的结果，其中实线圈中的峰值点即为目标峰值点。

图6给出了本文所提检测方法的检测概率、虚警率随位于主瓣内干扰个数、干信比(各干扰功率相等)的变化情况。实验中主瓣内噪声压制干扰源增加到7个，干扰源俯仰角分别为-0.5°，-1°，-1.5°，0.2°，0.5°，1°和1.5°，极化角分别为0, π/4，π/8，π/6，π/3，π/7和π/9。方位-俯仰网格尺寸均为0.1°。

由图6可以看出：1)当主瓣内干扰个数增大到某一数目时，检测概率迅速下降，这是因为干扰个数增加，使得目标临近的干扰谱峰增加，导致目标谱峰不能通过CFAR有效检测出来，进而无法进行进一步的判别。2)当主瓣内干扰个数增大到某一数目时，虚警率也会迅速上升，这是因为相邻干扰混入同一网格，进而导致该网格检测统计量超过检测门限，被错误地判为目标。

4 结束语

本文针对主瓣多点源干扰中目标难以检测的问题，放弃基于干扰能量抑制或提升信干噪比的传统思路，转而利用有源干扰与雷达目标在极化散射特性响应特征方面的差异，立足于雷达发射极化分集体制，提出了一种基于极化-空间谱特征的目标检测方法，可有效提升雷达在主瓣多点源干扰环境下的目标检测能力，为低波段雷达适应民用射频干扰环境、情报/制导雷达对抗主瓣多点源干扰以及主瓣变极化干扰提供有力支撑。

本文推导得到了检测统计量及其检测门限，通过仿真实验验证了该方法的基本检测性能。下一步，应充分提取目标与干扰极化分布特征差异并改进方法，提高主瓣相邻干扰、变极化干扰等复杂干扰情况下目标检测的有效性和稳定性。

参考文献：

[1] NATHANSON F E. Adaptive Circular Polarization[C]∥IEEE International Radar Conference, Arling-ton, VA: IEEE, 1975:221-225.

[2] GIULI D, FOSSI M, GHERARDELLI M. A Technique for Adaptive Polarization Filtering in Radars[C]∥IEEE International Radar Conference, Arlington, VA: IEEE, 1985:213-219.

[3] GHERARDELLI M, GIULI D, FOSSI M. Suboptimum Polarization Cancellers for Dual Polarization Radars[J]. IEE Proceedings, 1988, 135(1):60-72.

[4] 施龙飞, 王雪松, 徐振海, 等. APC迭代滤波算法与性能分析[J]. 电子与信息学报, 2006, 28(9):1560-1564.

[5] 任博, 罗笑冰, 邓方刚, 等. 应用极化聚类中心设计快速自适应极化滤波器[J]. 国防科学技术大学学报, 2015, 37(4):87-92.

[6] 毛兴鹏, 刘爱军, 邓维波, 等. 斜投影极化滤波器[J]. 电子学报, 2010, 38(9):2003-2008.

[7] SHOWMAN G A, MELVIN W L, BELENKII M. Performance Evaluation of two Polarimetric STAP Architectures[C]∥IEEE Radar Conference, Huntsville, AL: IEEE, 2003:59-65.

[8] FANTE R L, VACCARO J J. Evaluation of Adaptive Space-Time-Polarization Cancellation of Broadband Interference[C]∥IEEE Position Location and Navigation Symposium, Palms Springs, CA: IEEE, 2002:1-3.

[9] 毛兴鹏, 刘永坦, 邓维波. 频域零相移多凹口极化滤波器[J]. 电子学报, 2008, 36(3):537-542.

[10] 吴迪军. 机载雷达极化空时自适应处理技术研究[D]. 长沙: 国防科学技术大学, 2012.

[11] SHI Longfei, REN Bo, LI Yongzhen, et al. Joint

Filtering Scheme of Multistation GSM Interference for UHF-Band Radar[C]∥IEEE International Conference on Signal Processing, Communications and Computing, Kumming: IEEE, 2013:1-5.

[12] 施龙飞, 王雪松, 肖顺平. 转发式假目标干扰的极化鉴别[J]. 中国科学: F辑 信息科学, 2009, 39(4):468-475.

[13] ZONG Zhiwei, SHI Longfei, WANG Xuesong. A Commonality Used to Discriminate Active Repetition False Targets based on Polarization Characteristics of Antenna [J]. IET Radar, Sonar and Navigation, 2016, 10(7):1178-1185.

[14] 徐振海, 王雪松, 肖顺平, 等. 极化域-空域联合谱估计[J]. 国防科技大学学报, 2004, 26(3):63-67.

[15] 宗志伟. 弹道中段目标极化雷达识别方法[D]. 长沙: 国防科学技术大学, 2016:52-53.

[16] 盛骤, 谢式千, 潘承毅. 概率论与数理统计[M]. 3版. 北京: 高等教育出版社, 2001:168-169.