基于转差频率矢量控制的异步电动机动态性能仿真
2018-05-23马海心
马海心
(陆军装甲兵学院,北京 100072)
交流异步电动机结构简单、维护方便、运行可靠、价格便宜,但是由于磁链耦合非线性等特点,控制起来比较困难。采用矢量控制可以把交流电动机等效成直流电动机模型,从而借鉴直流电动机的控制思想对交流电动机进行控制。
直接对转子磁场定向矢量控制是比较复杂的,而采用转差频率控制的方法可以避免对磁链信号进行观测。转差频率矢量控制以转差角频率为输入量,以坐标变换为工具,以转矩和转速为控制目标,具有结构简单、易于实现、减少繁琐的磁链变换、控制精度高等优点。所以,转差频率矢量控制结合了矢量控制的思想和转差频率控制策略的优点,是对异步电动机控制的一种较为先进的方法。本文就是基于此方法展开研究与实验验证的。
1 矢量控制理论
1.1 矢量控制基本思想
矢量控制是目前异步电动机控制领域比较先进的控制方法,通常把含有矢量变换的交流电动机控制方法都称为矢量控制。
矢量控制系统的基本思路是把建立等效的旋转磁动势作为准则,把三相交流异步电动机中静止三相坐标系上的定子电流通过坐标变换等效成两相同步旋转坐标系上的直流电流,并对等效的直流电流分别控制,就可以实现磁通和转矩的解耦控制,从而达到近似直流电动机的控制效果。
矢量变换的原理及等效直流电动机模型如图 1所示。图中iA、iB、iC表示异步电动机输入端定子交流电流,通过3/2变换(Clark变换)可以等效成两相静止的正交坐标系中的交流电流isα和isβ,再经过与旋转转子磁链同步的旋转变换(Park变换),就可以等效成与转子同步的旋转正交坐标系上的直流电流 ism和 ist。ism和 ist分别为等效的励磁分量和转矩分量,并且已经实现了解耦。
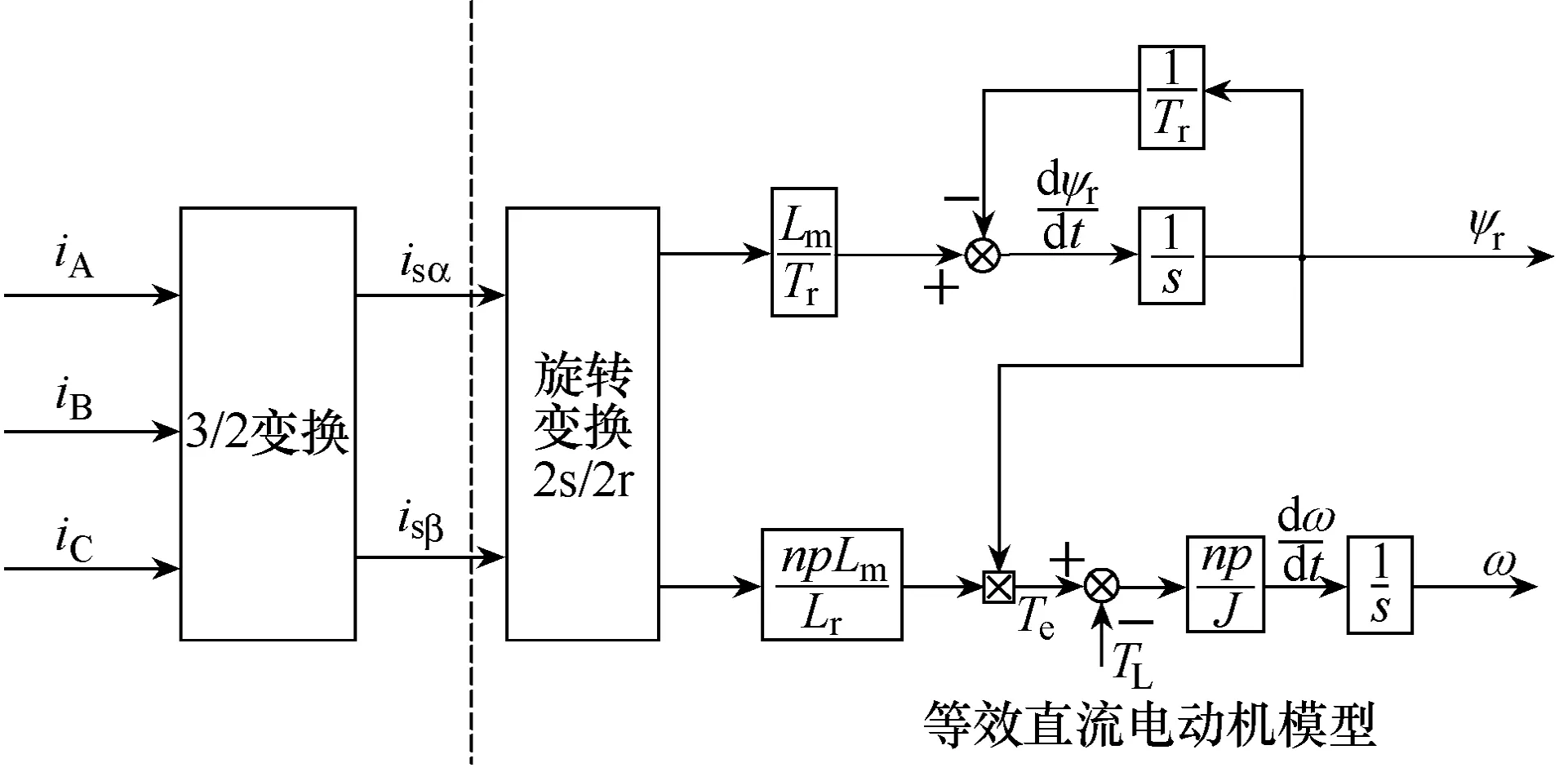
图1 矢量变换原理图及等效直流电机模型
通过调节 ism和 ist可以方便调节电动机的转矩和转速,把ism和ist再通过两相旋转到三相静止的坐标变换,就可以得到对应的三相交流电的输入值iA、iB和iC,从而调节异步电动机的转矩和转速。
1.2 坐标变换
矢量控制主要涉及交流电动机中交流电的坐标变换,一般包括三相静止到两相旋转及其逆变换。三相静止到两相旋转变换分两步完成,第一步是把三相静止坐标变换为两相静止坐标,即Clark变换;第二步是把两相静止坐标变换为两相旋转坐标,即Park变换。
在交流异步电动机三相对称绕组中通以三相对称的交流电,就会在定转子气隙中产生旋转的磁场,保证功率不变的前提下,按磁动势相等的原则,用两相对称绕组产生的旋转磁场来等效三相对称绕组产生的旋转磁场。设 iα、iβ分别为两相对称绕组的电流,iA、iB、iC分别为三相对称绕组的电流,它们之间的变换关系为

式中,i0是为了形式上变换方便而增加的一组零序分量,并不影响变换效果。
在静止的两相绕组中,通入两相平衡的交流电流,会产生旋转磁动势。如果使两相静止绕组旋转起来,并且旋转角速度等于旋转磁动势的角速度,那么在两相绕组中通以直流电流就可以产生等效的旋转磁动势。这就是两相静止坐标系到两相旋转坐标系变换的基本思想,这种坐标变换称为两相旋转-两相静止变换,简称 C2s/2r变换。设 iα、iβ为两相静止对称绕组中的电流,id、iq为两相旋转对称绕组中的电流,变换关系为

式中,ϕ 为 d-q 坐标系 d 轴与α-β 坐标系α 轴之间的夹角。
2 转差频率控制原理
对异步电动机转子磁链的直接进行检测比较困难,而且误差难以控制,在实际应用中多采用间接的方法,即根据容易测量的电压、电流或者转速等物理信号,结合转子磁链模型,通过计算得出磁链的幅值及空间位置信息。
在电气传动控制系统中,遵循的基本运动方程式为

式中,Te为电磁转矩;TL为负载转矩;J为机电系统的转动惯量;Pn为异步电动机极对数;ω 为转子旋转角速度。从式(3)不难看出,异步电动机的电磁转矩和转子角频率的变化率密切相关,通过控制转差角频率ωs就可以控制电磁转矩Te,从而可以达到间接控制转速的效果。
转差频率控制避免了对磁链的直接观测带来的不便于误差以及繁琐的计算,采用易于得到的转差角频率,通过简单计算就可以得到转矩分量和励磁分量,进而实现对异步电动机的快速、有效调节。这种控制方法使电动机的定子电流频率能够在转速变化过程中,始终跟随转子的转速实现同步升降,让转速调节变得更加平滑。结合坐标变换,转差频率矢量控制的异步电动机调速系统原理如图2所示。
图2中,ω*表示设定的转差角频率;别表示等效模型中定子电流励磁和转矩分量,由于本设计采用电压型逆变器供电,可以把电流量转换为电压量,转换关系为

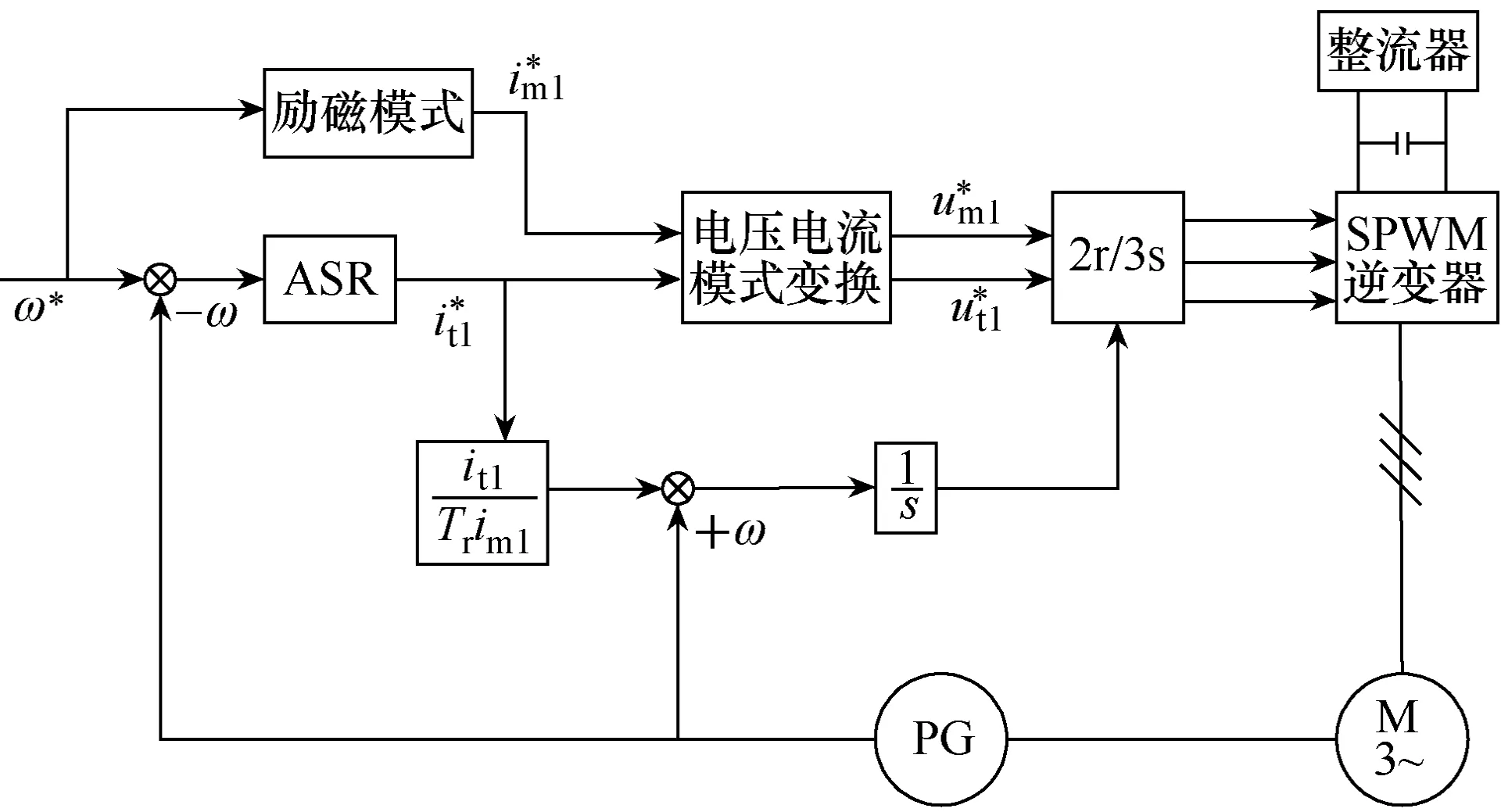
图2 转差频率矢量控制的原理框图
式(4)和式(5)中,um1、ut1分别表示等效模型中定子电压的励磁和转矩分量;σ 为漏磁系数,σ =1−/(LsLr);Rs、Ls为定子电阻和电感;p 为微分运算。
um1、ut1从两相旋转坐标系变换到三相静止坐标系,得出SPWM逆变器的三相电压控制信号,由此来控制逆变器的输出电压。
3 仿真模型搭建
3.1 仿真系统
转差频率矢量控制的系统仿真模型如图 3所示。该系统模型主要包含有给定模块、PI调节模块、函数运算模块、坐标变换模块、PWM脉冲发生器模块、电压型逆变器模块和交流异步电动机模型。模型中还包括一些观测窗口,如电流、电压观测窗口,转速-转矩二维显示窗口,磁链轨迹二维显示窗口。
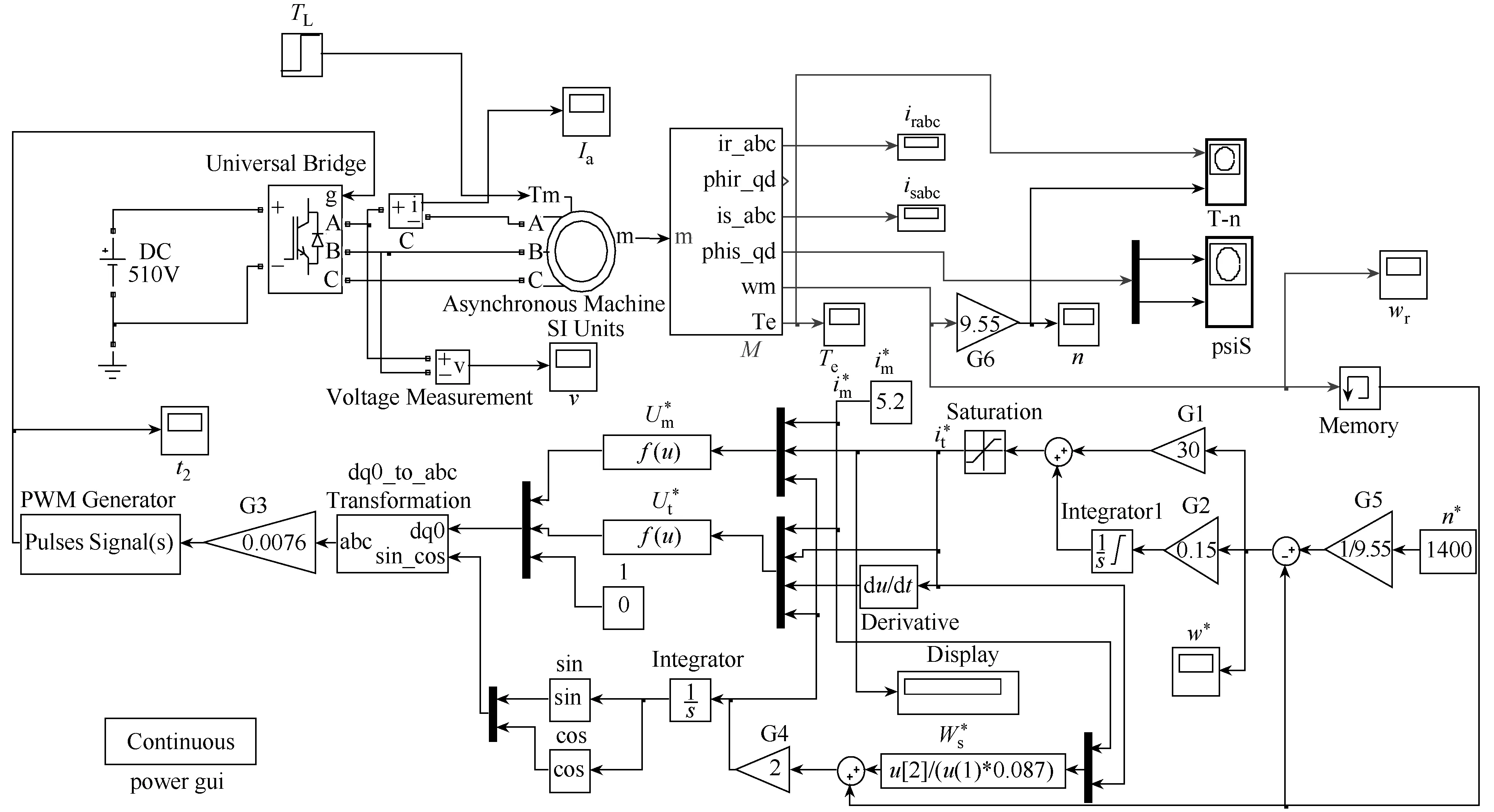
图3 转差频率矢量控制系统仿真模型
3.2 模型设定
给定模块中,给定值包括转子目标转速n*和电流励磁分量。设置n*为1400r/min,为5.2A。
PI调节模块就是由比例环节和积分环节构成的。本模型中,对目标转速和实际测量转速的差值进行比例积分运算,得到电流转矩分量。
函数运算模块是对式(4)和式(5)的模型实现,把电流量转换为电压量。
坐标变换模块是把两相静止的 dq坐标系转化为三相交流abc坐标系,此模块是Simulink库中打包好的,可以直接使用。
PWM脉冲发生器模块是3桥臂6路触发结构,可以产生逆变器各桥臂的开关信。该发生器的载波频率设定为 500Hz,载波频率越高,电动机运行越平稳,但是也会使电动机损耗增加。设定载波频率需要视实际情况确定。
电压型逆变器模块把直流电变换为需要的交流电。本模型是将510V直流电,根据PWM脉冲发生器的给出信号,产生相应的交流电。该逆变器的开关管选用IGBT,参数设定为:关断电阻10kΩ,导通电阻0.001Ω,导通压降为0.5V,下降时间1μs,拖尾时间2μs。续流二极管导通压降设置为0.2V。
该模型的异步交流电动机参数主要包括:额定电压380V、额定频率50Hz、极对数为2,Rs=0.435Ω,Rr=0.816,L1s=0.002mH,Lm=0.069mH,J=0.19kg·m2,转子时间常数为Tr=Lr/Rr。逆变器直流电源为510V。该模型中的函数运算关系分别见式(4)和式(5)。模型中放大参数见表1。

表1 转差频率矢量控制仿真模型放大器参数
4 仿真结果
4.1 仿真波形
该仿真模型设定转速n*为1400r/min,给定定子电流励磁分量为5.2,在t=0.45s时,突然给定负载转矩TL=65。由于该系统较为复杂,为了使仿真计算收敛,仿真算法采用固定步长算法ode5,步长取10−5。模型的仿真结果分别如图4至图8所示。
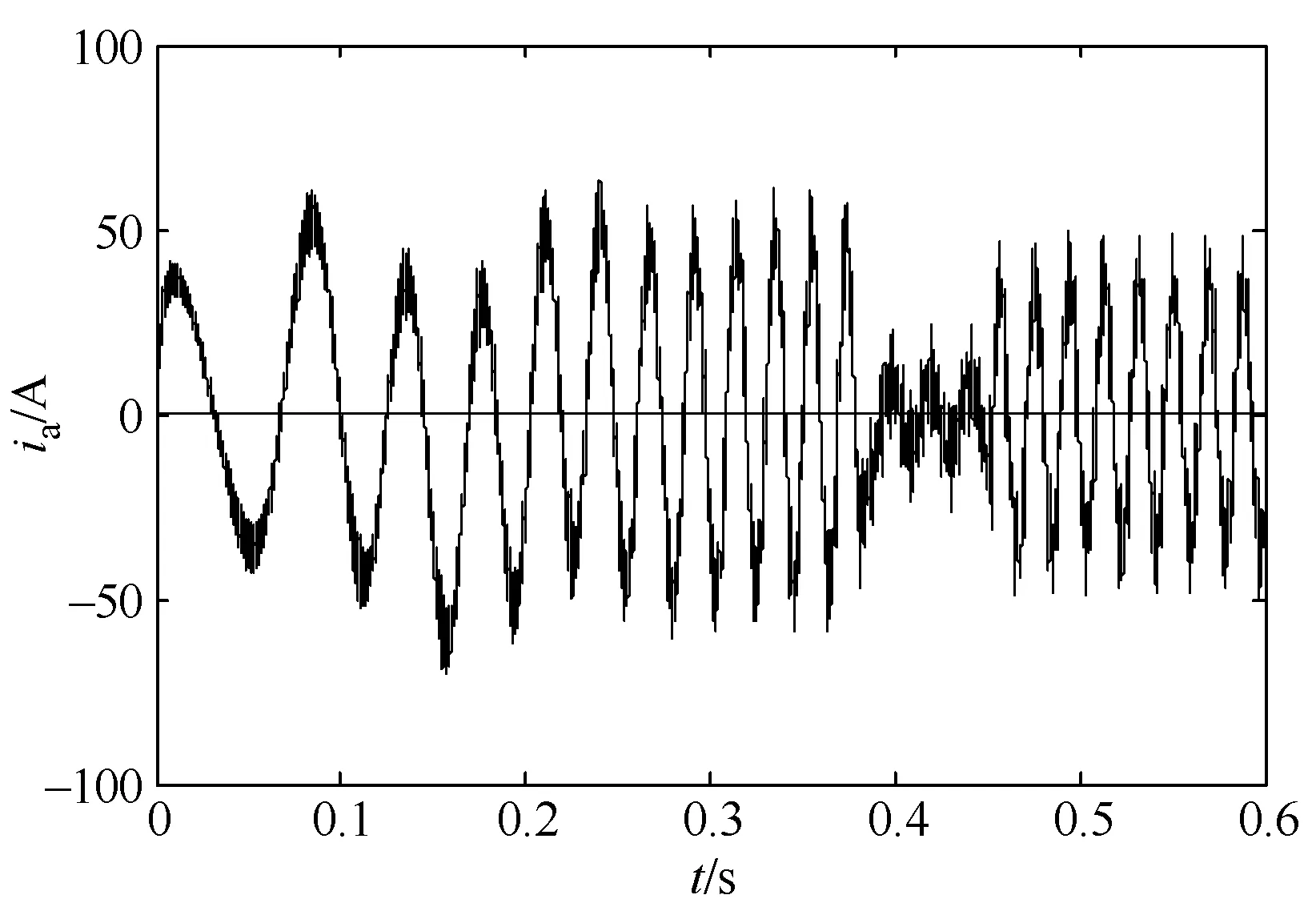
图4 定子A相电流响应

图5 转速响应
4.2 仿真分析
通过图4至图6中的仿真结果图可以看出,在交流异步电动机起动过程中,定子A相电流幅值较大达到40A左右,频率较低,随着转速持续上升,电流基本保持不变,转矩基本维持不变。在 0.38s时刻,转速达到给定转速1400r/min,电流幅值迅速下降至20A左右,转矩也迅速下降。到0.45s时,突然增加负载转矩为65N·m,定子A相电流和转矩开始迅速上升,但是转速的波动很小,基本维持在1400r/min。在图4、图5和图6中显示的异步电动机起动和受到负载冲击时的特性,充分显示了转差频率矢量控制在维持恒转矩起动和维持转速稳定方面的优良特性。
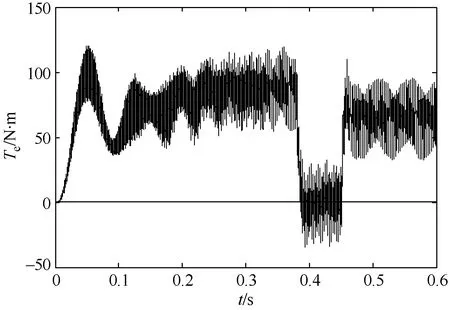
图6 电动机输出转矩变化

图7 转矩-转速特性
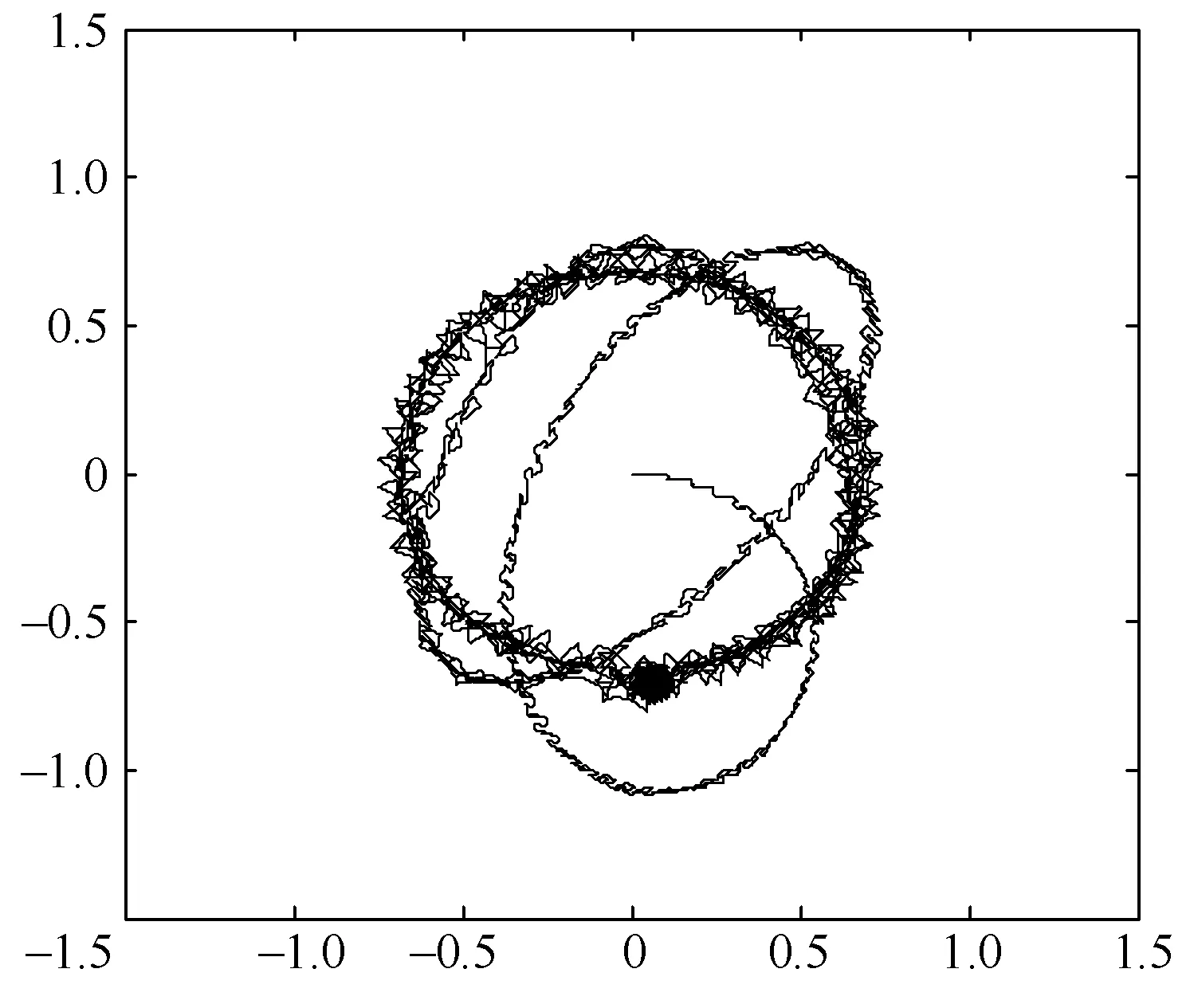
图8 定子磁链轨迹
图7是异步电动机转速-转矩特性,从图中可以看出,在起动过程中,转矩先是随着转速的上升而振荡上升,随着磁链的稳定,转矩维持在80N·m左右。在 0.38s时刻,转速达到给定值后,转矩又迅速下降。图8显示了异步电动机模型定子磁链的变化过程。可以看出,在电动机刚开始起动时,磁链是不规则的形状,这导致了转矩的大幅度波动。到0.2s后,磁链运行轨迹基本为规则的圆形,这也使得转矩能够保持稳定。
5 结论
本文介绍了矢量控制基本思想和转差频率控制的控制策略,在Simulink中搭建仿真模型,实现转差频率矢量控制的仿真验证。仿真结果表明,转差频率矢量控制策略具有良好的起动性能,在突加负载的情况下,也能较好维持转速稳定,说明转差频率矢量控制系统动态性能良好。
参考文献
[1] 韩智玲. 应用在交流传动试验台中的差频原理的理论推导[J]. 电气技术, 2012, 13(11): 75-77.
[2] 陈伯时, 陈敏逊. 交流调速系统[M]. 北京: 机械工业出版社, 1998.
[3] 彭景金, 蒋程, 江园园. 基于Simulink的转差频率矢量控制的建模和仿真[J]. 电气开关, 2015(5): 63-69.
[4] 彭伟发, 徐晓玲, 邹娟. 转差频率矢量控制仿真研究[J]. 华东交通大学学报, 2009, 26(1): 67-70.
[5] 洪乃刚. 电力电子, 电机控制系统的建模和仿真[M].北京: 机械工业出版社, 2010.
[6] 王治国, 郑泽东, 李永东, 等. 轨道交通车辆牵引电传动系统的调制与控制策略[J]. 电工技术学报,2016, 31(24): 222-232.
[7] 邵佳俊, 黄文新, 杨驹丰, 等. 基于定子电流矫正的异步电机间接定子磁场定向控制[J]. 电工技术学报,2016, 31(23): 31-37.
[8] 周喆, 吴俊, 杨俊祥. 异步电动机无速度传感矢量控制研究[J]. 电气技术, 2016, 17(12): 41-44.
[9] 卜飞飞, 黄文新, 胡育文, 等. 基于瞬时转差频率控制的定子双绕组异步电机变频交流发电系统[J]. 电工技术学报, 2012, 27(7): 93-100.
[10] 魏宇峰, 胡文斌. 无位置传感器异步电机矢量控制系统研究[J]. 电气技术, 2016, 17(8): 19-23.
