纤维-絮凝体二元堵水体系阻力计算方法研究

张宪法，王继伟，魏 驰，杨旭刚，李俊儒，陈付真

1 研究背景

目前我国部分油田进入中高含水期，由水窜导致的含水率快速上升、采出程度低等问题突出，因此调剖堵水作为一项经济有效的提高采收率手段得到了广泛应用。常用的堵水方法包括机械堵水和化学堵水。机械堵水工具主要包含堵水管柱以及相应的封隔器，其中堵水管柱有可钻式、整体式、悬挂式以及平衡式四种类型。油田实际开采进入到中高含水期之后，机械堵水技术逐渐向可调层技术以及液压可调层技术两方面发展[1-2]。化学堵水是通过将化学堵剂注入出水层位，利用堵剂的化学性质或化学反应物的物理化学性质达到封堵地层出水孔道、降低油井综合含水率的目的[3]。目前常用的化学堵剂主要有水泥类堵剂、树脂类堵剂、无机盐沉淀类堵剂、水溶性聚合物冻胶类堵剂、颗粒类堵剂以及泡沫类堵剂等[4]。

目前油田化学堵水大量使用由聚合物和交联剂交联形成的絮凝体作为堵剂，但絮凝体不耐冲刷、容易被突破等问题严重影响其堵水效果[5-9]。通过在絮凝体中加入弹性纤维，形成纤维-絮凝体二元堵水体系，为解决上述问题提供了新的思路。在该二元体系中，纤维在孔隙中与壁面接触，搭建形成二元体系骨架，受力后产生弹性反力；絮凝体充填骨架体系，与孔隙接触产生摩擦力、粘滞力，同时与纤维协同作用，提高二元体系强度。赵修太等人进行了纤维-冻胶的联合堵水实验，对比分析了冻胶体系与纤维-冻胶二元体系在不同温度与不同pH值影响下的堵水效果，结果显示两者在同等 pH值和温度条件下，纤维-冻胶二元体系在封堵率、突破压力、孔隙体积减小程度上均优于冻胶体系，同时实验结果也表明二元堵水体系封堵率比絮凝体封堵率提高31.68%[10]。

目前纤维-絮凝体二元堵水体系研究主要集中在室内实验方面，得到的结论主要为宏观统计规律，微观机理尚不明确，纤维和絮凝体联合作用的理论研究尚不完善。为此，本文开展了纤维-絮凝体二元堵水体系理论研究。首先借鉴材料力学的纯弯曲梁变形特性[11]，并结合泰勒公式变换以及概率论中常用概率模型等数学工具[12]，构建了纤维在堵水时的阻力计算模型；其次基于非牛顿流体的流体力学理论，给出了考虑屈服应力的絮凝体堵水阻力模型[13]；与此同时，根据相界面法及摩擦阻力计算方法[14]，给出了通过相界面表示的絮凝体堵水阻力的计算模

2 纤维阻力计算模型

2.1 纤维单体阻力计算

型；最后将纤维和絮凝体的阻力计算模型进行耦合，建立了一维纤维和絮凝体二元体系联合堵水时的堵水阻力模型，并根据实验条件的不同进行了优化。在纤维阻力计算模型中，首先研究单根纤维在等直径毛细管中所产生的阻力。假设长度为L的单根纤维垂直置于等直径毛细管中，毛细管直径为 D，外力为F，F为均匀力场，纤维变形如图1所示。

图1 纤维受力计算模型

根据力的平衡原理可知纤维所产生的阻力fF即为纤维所受外力：fF=F×D；根据材料的纯弯曲变形挠曲线方程关系可知：

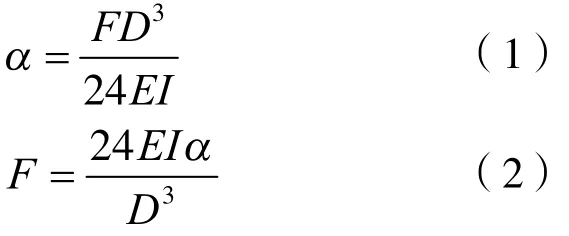
由于纤维在毛细管中的变形近似为弧形，经过几何变换得：

将sinα用泰勒公式展开，经变换得：

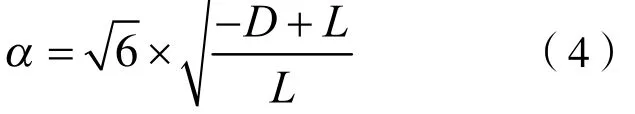
惯性矩为：

将公式（4）和（5）代入式（2）得纤维弹性阻力计算模型如下：

式中：F为纤维所受均匀力场，N/m；fF为纤维弹性阻力，N；α为圆心半角，Rad；D为毛细管直径，m；L为纤维长度，m；E为纤维弹性模量，Pa；d为纤维截面圆的直径，m；I为纤维的惯性矩，m4。

根据公式（7）可知纤维的阻力受纤维弹性模量、纤维直径、纤维长度以及孔隙直径影响[15]。假设纤维的弹性模量E=106Pa、孔隙直径D=1cm，对纤维弹性阻力与纤维长度和纤维直径的关系进行研究，得出纤维属性参数对阻力影响规律如图2所示。

由图2可知，在纤维长度与孔隙直径之比一定时，纤维弹性阻力随纤维直径的增大而增长，所以为提高堵水效果，应尽可能选用直径较大的纤维。纤维弹性阻力的增长幅度随纤维长度与孔隙直径之比的增大而增大。纤维长度与孔隙直径之比在 1～2之间时，弹性阻力增长幅度变化比较明显；纤维长度与孔隙直径之比大于3后弹性阻力增长幅度不明显，故纤维长度与孔隙直径之比存在最优值。

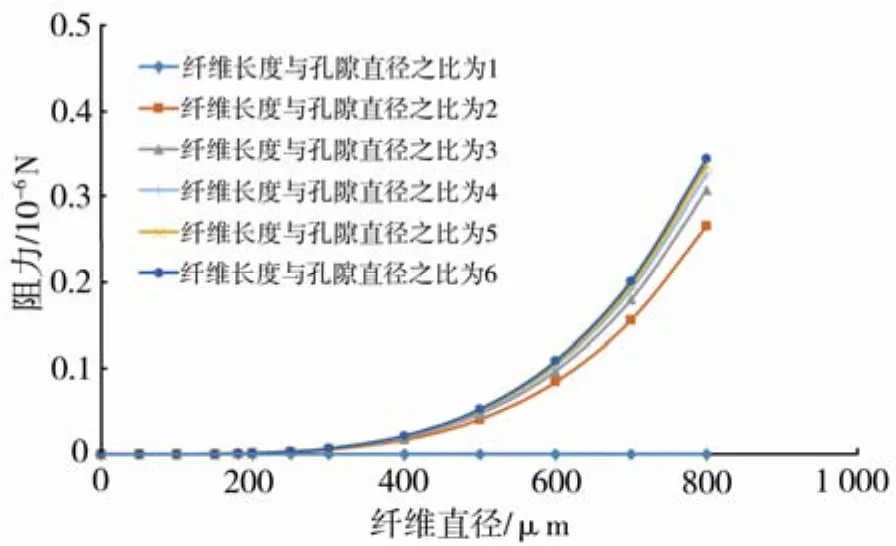
图2 纤维属性参数对阻力的影响

图3可得出，纤维弹性阻力随纤维长度与孔隙直径比值的增加而增大，当比值达到3时上升趋势变缓，曲线逐渐平稳。所以可以推断孔隙直径一定时，对应纤维阻力纤维长度有最佳值。从图中得出结论，纤维长度与孔隙直径之比最优值为3。

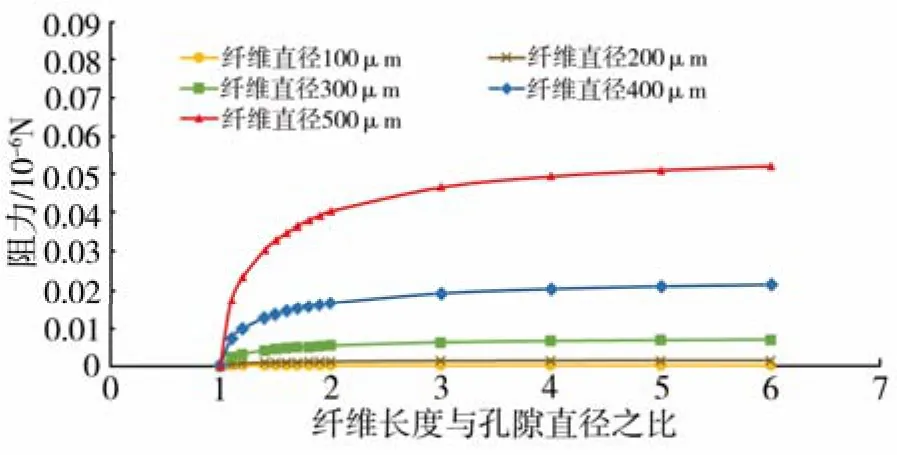
图3 纤维属性参数对阻力的影响

2.2 纤维概率分布模型

当多根纤维同时注入孔隙中时，纤维在孔隙中分布具有不确定性，纤维与孔隙壁面接触角度不同时其对有效阻力的贡献程度也不同。因此，在计算纤维有效阻力时需要考虑纤维在孔隙中的分布状态和分布规律。

假设单位时间内有n根纤维注入注水井，若有n～ m根滞留在储层中，则有效纤维比例为：

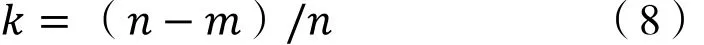
对于滞留在孔隙中的纤维，其分布主要为图 4所示的三种形态。纤维两端连线与孔壁夹角为γ，已知γ的取值范围为：

由图5可知，γ在0.5π附近时纤维易在孔隙中滞留，即纤维与孔隙壁面角度呈γ=0.5π时概率最大，在 角 度 γ1= a rcsin（ D / L）或时概率最小，近似为0。这一分布规律与正态分布相吻合，因此假设纤维在孔隙中的概率分布符合正态分布。

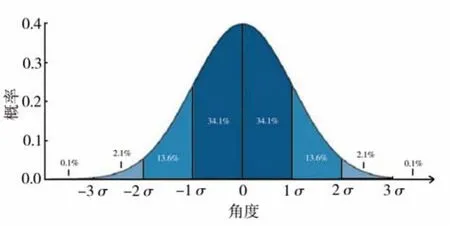
图5 纤维分布概率

正态分布的概率分布密度为：

式中：μ为常数，等于0.5π；σ为常数，纤维以γ=0.5π角度滞留在孔隙中的概率。

根据归一化条件，即：

通过式（11）可求得σ的值。

长为L的纤维倾斜在孔隙中产生的阻力，相当于纤维投影在竖直方向上纤维长度在孔隙中产生的阻力，即相当于长为 sinL γ的纤维垂直与孔隙壁面时在孔隙中产生的阻力。基于纤维弹性阻力计算模型，以任意形状滞留在毛管中的纤维产生的阻力为：

对于注入的n根纤维，产生的总阻力tfF为：

上式即为假设纤维在孔隙中的分布形态符合正态分布时，纤维总阻力计算模型。

3 絮凝体堵水阻力模型

3.1 屈服应力法

絮凝体是由一种线型高分子经过交联后产生的具有网状结构的化学物质，具有一定的连续性和稳定性。在调剖堵水过程中，絮凝体能够滞留在孔隙中有效封堵水窜通道。从流变模式上说，絮凝体是一种非牛顿流体（塑性流体），它具有与牛顿流体不同的流变特性，絮凝体流动存在启动屈服应力[16]，该启动屈服应力也就是絮凝体能够承受的最大应力。当流体压力超过启动屈服应力时，絮凝体产生形变开始流动，因而失去封堵效果。絮凝体产生的堵水阻力为：

式中：jF为絮凝体产生的阻力，N；sτ为絮凝体塑性流体的启动屈服应力，可由实验确定，Pa；A为絮凝体与孔隙的接触面积，可根据絮凝体的体积和孔隙的半径求得，m2。

这种计算絮凝体阻力的方法，是根据实验现象推导出来的，是从宏观角度考虑问题得到的絮凝体阻力计算模型。

3.2 相界面法

注入水与絮凝体之间存在相界面，相界面上的分子受两相的引力大小不同，产生了界面张力。对于相界面的曲界面来说，其两侧的压力不同，此曲界面压差是堵水阻力的一部分。

根据界面化学理论，水与絮凝体产生的曲界面压差为：

式中：cP为曲界面压差，Pa；σ为水与絮凝体的界面张力，N/m；θ为水对絮凝体的润湿角，Rad；r为毛细管孔隙的半径，m。

已知当0θ=即cos1θ=时，cP取得最大值，为：

此时，由相界面产生的絮凝体阻力最大，为：

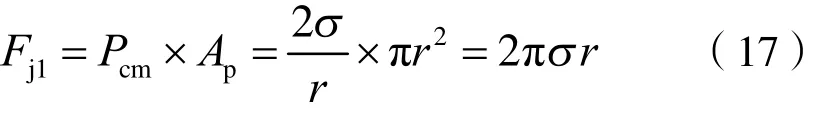
式中：pA是毛细管孔隙的横截面积，m2。

除了相界面压差外，水与絮凝体相界面还存在静摩擦力，在絮凝体未被突破前，絮凝体与孔隙壁之间的静摩擦力大小为：

式中：N为正压力，N；η为摩擦系数。

式（18）中正压力N可根据水与絮凝体相界面张力求得：

将式（19）代入式（18）可得絮凝体产生的阻力为：

当sin1=θ时，絮凝体产生的阻力最大，为：

将上述絮凝体曲界面压差和静摩擦力进行耦合，可得絮凝体产生的阻力为：

相界面法计算絮凝体堵水阻力，是从微观角度考虑絮凝体阻力问题，与屈服应力法并不矛盾，这两者可以相互补充，同时也可以相互验证。

4 二元体系堵水阻力模型

纤维与絮凝体在储层中产生复合堵水网络体系，二元体系在孔隙中的分布形态如图6所示。

将纤维阻力模型与絮凝体阻力模型进行耦合得到纤维-絮凝体复合网络的阻力计算模型为：

式中：a为纤维叠加阻力系数；b为絮凝体叠加阻力系数。a、b可根据实际条件的不同，通过室内实验进行求得。

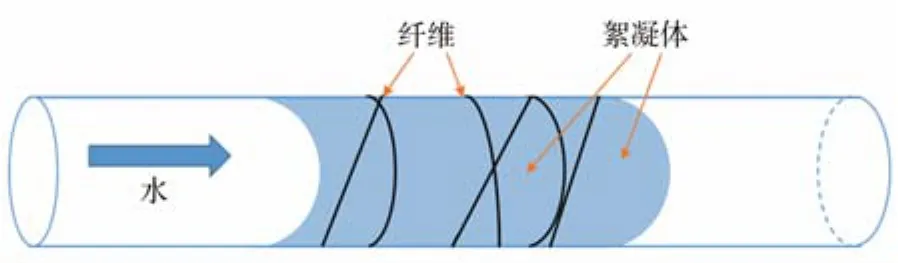
图6 纤维-絮凝体复合堵水网络体系示意图

最后，通过VB软件进行了计算模型的编译，实现了单根纤维在堵水时的阻力、絮凝体单独堵水时的阻力以及纤维-絮凝体二元网络堵水体系堵水阻力的计算，从而提高了纤维-絮凝体二元体系优化的效率。

5 结论

（1） 建立了纤维在一维二元网络堵水体系中的阻力计算模型，分析了纤维属性参数对纤维阻力影响规律，得到了纤维长度与孔隙直径之比最优值为3。

（2） 基于屈服应力法和相界面法分别建立了絮凝体在一维二元网络堵水体系中的阻力计算模型，两模型可以相互补充，同时也可以相互验证。

（3） 研究了纤维在多孔介质中的分布规律，建立了纤维分布概率模型。在此基础上实现了纤维与絮凝体阻力模型的耦合，得到纤维-絮凝体一维二元网络联合堵水体系阻力计算模型。

参考文献：

[1] 章秀平.堵水调剖技术在油田发展中的应用[J].化工管理，2016，29（6）：128.

[2] 尤建华，王卫真.油田机械堵水技术发展研究[J].科技风，2016，29（15）：141.

[3] 吴玉柱，严慧呈，杨小东.油田化学堵水工艺技术[J].化学工程与装备，2016，45（7）：88–89.

[4] 柯耀斌.论油田化学中堵水调剖的开发及应用[J].中国石油和化工标准与质量，2017，37（3）：62–63.

[5] 刘文龙，张杰，赵英杰，等.油田化学耐盐堵剂研究进展[J].内蒙古石油化工，2011，21（18）：30–34.

[6] 刘玉章.聚合物驱油提高油田采收率技术[M].北京：石油工业出版社，2006.

[7] D D WHITNEY，徐文芹.聚合物凝胶体系的堵水试验[J].国外油田工程，1999，14（7）：25–29.

[8] 周彬，王慧玲，樊理山，等.含胶类纤维成膜装置的设计及实验[J].上海纺织科技，2013，40（10）：21–22.

[9] 任建晓，林涛，殷学风，等.细小纤维与CPAM共絮凝体的性质[J].湖南造纸，2013，32（4）：3–11.

[10] 赵修太，董林燕.纤维–聚合物冻胶复合堵水体系研究[J].精细石油化工，2013，29（4）：18–21.

[11] 范钦珊，唐静静.工程力学（静力学和材料力学）[M].北京：高等教育出版社，2007：7–10.

[12] 王清河，常照光，曹晓敏，等.随机数据处理方法[M].东营：中国石油大学出版社，2011.

[13] 祝连庆，董明利，丁裕栋.非牛顿流体流变学特性测试与建模[N].北京机械工业学院学报，1997，12（1）：21–24.

[14] 曾作祥，孙莉.界面现象[M].上海：华东理工大学出版社，2016.

[15] 任志华，于永玲.影响亚麻纤维弹性的因素及其提高方法[J].大连轻工业学院学报，2002，22（3）：228–231.

[16] 张国忠，刘刚.大庆胶凝原油启动屈服应力研究[J].石油大学学报，2005，47（6）：91–93.