一种用于CDMA2000 1x导频捕获的自适应门限算法研究

王文实，夏文龙，郭庆功

(四川大学 电子信息学院，四川 成都 610025)

0 引言

无线通信技术迅速发展，在满足人们需求、为生活提供便捷的同时，特殊场合也需要对通信进行管制。3G移动通信采用扩频技术和码分多址技术，抗干扰能力很强，传统的压制式干扰效果不理想。实现可靠的3G移动通信屏蔽需要生成带有小区特征的干扰信号，准确捕获和跟踪基站信息是智能干扰的基本功能需求。3G制式中CDMA2000 1x使用PN长码调制导频，对CDMA2000的干扰首先要捕获PN码。PN长码捕获有滑动相关算法[1-3]、FFT快速相关算法[4-5]、匹配滤波器算法等。干扰仪仪器硬件资源有限，但又要求能快速捕获基站信息，单纯的串行、并行滑动相关算法或单一的FFT相关算法均不能满足其快速捕获、适应不同频偏、计算复杂度小的要求，因此考虑采用PMF-FFT短时相关算法。PMF-FFT算法多用于大频移高动态下GPS信号的捕获[6-8]，基于PMF-FFT的改进算法在低信噪比、高动态方面均具有良好效果,应用广泛[9-20]。其中文献[17]和[18]对功率图谱累积在PMF-FFT算法中的性能进行了仿真，前者针对高斯信道进行了仿真，后者针对多径信道进行性能的仿真，但使用的PN码较短。文献[19]将其用于CDMA2000制式下导频的捕获，捕获概率在低信噪比下较差分相干累积算法高，但仅在给定较小频偏下获得较好效果。文献[20]将PMF-FFT算法作为联合搜索算法的一个模块，对CDMA2000 EV-DO制式下空口上行信号进行了捕获，虽获得了较好效果，但缺乏对算法性能的研究。同时，为捕获微弱信号，文献[19]使用4 096的相关总长度，部分滤波器256个；文献[20]中相关总长度为215，部分滤波器1 024个，匹配滤波器长度为32。以上文献均采用固定门限，固定门限下PMF-FFT算法虽能捕获信号，但是算法复杂度大，需要的相关长度长，且固定门限在低信噪比、弱信号下存在漏检，噪声功率高时虚警概率又会提高。本文提出一种基于PMF-FFT短时相关的自适应门限捕获算法，使用功率图谱累积法增大弱信号下的峰值，使用自适应门限提高对低信噪比下的信号捕获，并在性能仿真的基础上实现空口基站信号的解调捕获。相关总长度为256、部分匹配滤波器16个时，成功完成空口基站信号的导频捕获。

1 CDMA2000 1x信道结构与处理模型

在算法捕获性能研究中，使用标准CDMA2000 1x信号作为初始输入，标准信号按照协议生成每个信道并合并为基带信号，没有附加噪声。仿真过程中，对初始输入信号进行QPSK调制，对调制后的信号加不同噪声功率的高斯白噪声，增加不同频偏以模拟高斯信道，然后解调，将解调后的数据作为PMF-FFT捕获算法的输入，进行后续计算捕获。信号前期处理过程如图1所示。

图1 仿真信号处理

2 PMF-FFT自适应门限算法原理

PMF-FFT是将部分匹配与FFT算法相结合的捕获算法，捕获原理如图2所示。整个系统包含P个部分匹配滤波器，每个部分匹配滤波器的长度为X，设M为总相关长度，则有M=X×P。PMF-FFT算法将信号捕获过程中对PN相位、对频率的二维搜索简化为对相位的一维搜索，通过分析FFT模值结果即可获得频偏估计结果，大大减小了捕获时间。

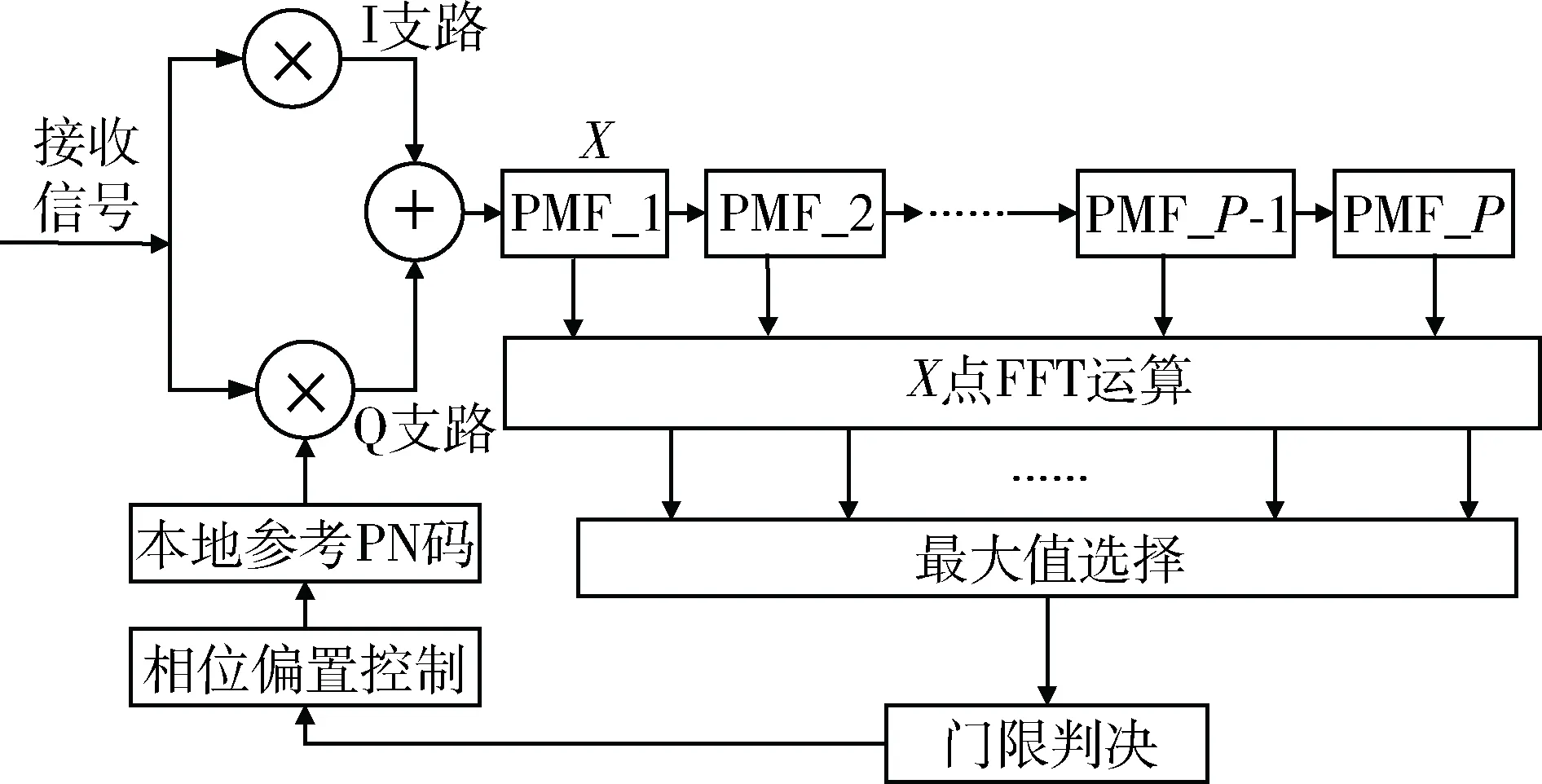
图2 PMF-FFT算法原理

PMF-FFT算法多采用周期图谱估计法进行平均功率估计，这种估计不仅有偏，且不是一致估计，当信噪比很低时，频偏谱线有可能被噪声谱线淹没，造成漏检。文献[17]提出功率谱累积平均法可以提高低信噪比下的峰值，同时还可以降低估计方差，获得较好的捕获效果，本文采用功率谱累积平均法以提高对弱信号的检测能力。

在PN码序列的捕获过程中，判决门限的高低影响捕获算法的性能。当判决门限过高时，在低信噪比下微弱信号的累积结果可能被漏检，造成检测概率的降低；而判决门限过低，又很容易导致噪声分量超过门限，造成虚警概率过高，同时虚警造成的惩罚捕获时间也会影响平均捕获时间。因此，门限的恰当与否，影响捕获算法3个最重要的性能指标。

对相关结果进行排序，除相关结果最大值外，其余相关值进行平均，设此平均值为PN，本文根据相关时得到的该平均值乘以一个比例系数来作为自适应门限，则捕获门限t为：

t=10α/10×PN

(1)

其中，α为比例因子。该自适应门限的优势在于既不会将噪声谱线纳入门限范围，减小了虚警概率，又能够保证对相关峰值的捕获，同时门限随信噪比而变化，提升了系统的检测概率。在FFT计算长度为256时，一般取α为11～13 dB。

(2)

其中:

(3)

虚警概率为:

(4)

在恒虚警概率处理下，可得归一化门限的限制条件为：

(5)

其中N为FFT的点数。

平均捕获时间是捕获算法最重要的性能指标之一，平均捕获时间采用单次驻留捕获判决方式。算法的平均捕获时间为：

(6)

其中，U为虚警判决惩罚因子，τd为搜索一个单元需要的检测驻留时间，在虚警的情况下，校验环节会增加捕获时间，增加的惩罚捕获时间值为Uτd。

3 仿真与结果分析

3.1 捕获概率仿真

根据文献[19]的分析结果，综合考虑算法复杂度和捕获性能，为方便计算对比，选择与文献中相同参数进行仿真，如表1所示。其中，M代表仿真的总相关长度，X表示PMF-FFT算法中的部分匹配滤波器的长度，fd表示设定的频偏，FFT点数是指计算中快速傅里叶变换的点数，T表示判决的门限。SNR为仿真进行的信噪比范围，Ec表示输入的标准CDMA2000 1x信号的功率，No表示噪声的功率，信噪比SNR可以表示为Ec/No。

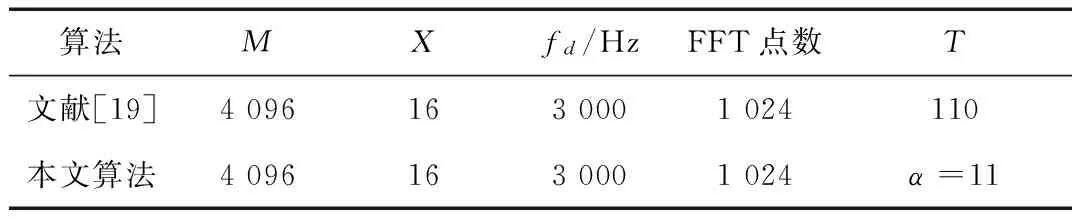
表1 仿真参数

使用标准CDMA2000 1x信号作为输入时，导频信道功率占总信道能量的0.1，因此导频信号与噪声的信噪比为(SNR-10) dB，仿真SNR范围为-27～10 dB，设导频信道的功率为pilot_Ec，相当于pilot_Ec/No范围为-37～0 dB。本文所有绘图均基于导频信噪比，即pilot_Ec/No。

在表1的仿真参数下，本文算法与文献[19]算法的捕获概率对比如图3所示，其中信噪比为pilot_Ec/No，信噪比为-28 dB时，本文算法捕获概率为0.8，文献[19]仅有0.15，说明自适应门限及功率图谱累加在提高弱信号下的捕获方面具有较好的效果。

图3 固定门限与自适应门限捕获概率对比

图3说明，在同等仿真条件下，与文献[19]相比，自适应门限能够显著提高捕获概率。

由于文献[19]中使用PMF-FFT周期图法进行计算，周期图法在低信噪比下可能造成漏检，因此对比周期图法和功率谱累加法进行仿真，根据文献[17]、[18]分析结果，M越大，捕获概率越高；累加次数越大，捕获概率越高，为简化计算，采用如表2所示参数进行仿真，其中算法1为周期图法，算法2为功率谱累加法，M为总的相关长度，X为单个部分相关器的长度，fd为多普勒频偏，蒙特卡洛重复计算次数为10 000次，累加次数均为5次，T_fixed代表固定门限值的设定，T_adaptive为自适应门限值的设定。

表2 仿真参数2

从图4可以看出，在同等参数设置下，使用同一种算法时，相比固定门限，使用自适应门限能显著提高低信噪比下的捕获概率；在相同的门限设置下，功率谱累加法比周期图法更加优越。

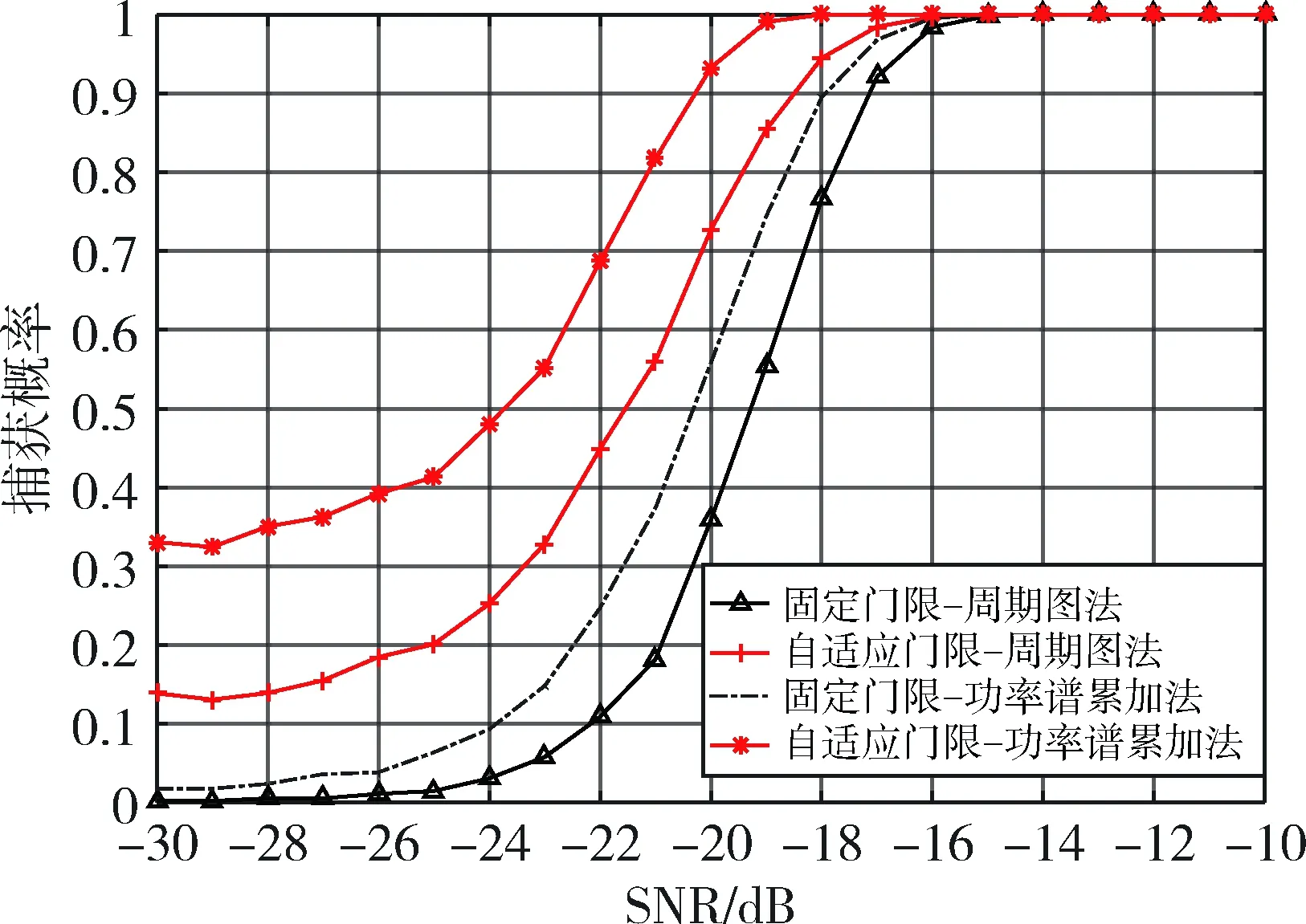
图4 不同门限设置下两种算法对比

3.2 平均捕获时间仿真

在同一相关长度下，本文算法复杂度与文献[19]基本持平，增加常数次加法，因此可认为捕获单个单元的时间相等。其中，捕获时间与τd成正比，设τd为单位1，因此此处捕获时间没有单位，为相对大小。表1计算参数下，仿真得到的平均捕获时间对比如图5所示。

图5 文献[19]与自适应门限平均捕获时间对比

可以看出，在低信噪比下，本文算法具有更小的平均捕获时间。在理论上，低捕获概率和高虚警概率导致较大平均捕获时间，而本文算法的捕获概率高于固定门限算法，因此，仿真结果与理论吻合。

根据式(6)，设定虚警概率为0.01，惩罚因子为30，τd为单位值1，对表2参数下的仿真结果的平均捕获时间进行对比分析。图6为自适应门限及固定门限下周期图法与功率谱累加法的平均时间对比，图7为放大之后的自适应门限下两种算法的平均捕获时间对比，为方便绘图，将所有输出结果除以104。

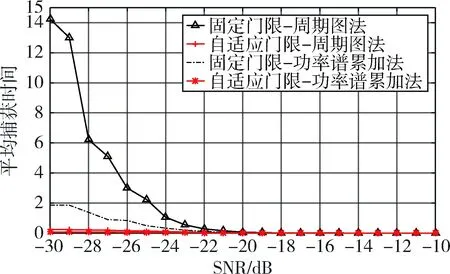
图6 表2参数下平均捕获时间对比

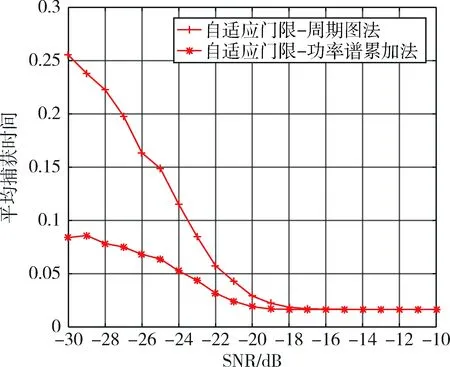
图7 自适应门限下两种不同算法平均捕获时间对比

从图6和图7可以看出，低信噪比时，同一种算法在固定门限下的平均捕获时间比自适应门限大很多，而无论是自适应门限还是固定门限，功率谱累加法的平均捕获时间均小于周期图法。由此可以看出，自适应门限下使用功率谱累加法的PMF-FFT算法是性能比较优越的。

4 空口信号解调与结果分析

在仿真结果基础上，使用PMF-FFT功率图谱累加自适应门限算法对空口信号进行捕获以检验其性能。使用FPGA硬件平台及接收天线对基站空口信号进行采集。CDAM2000 1x经过频段重耕之后，各地区使用不同频点，最常使用的是载频号为283与242的频段，选择283频段进行信号采集，空口信号采集参数如表3所示。

表3 空口信号参数

解调结果如图8所示。其中图8(a)为三维搜索结果图，数据长度为16，方向为频域方向，另一维为时域序列，可以看出在时频二维联合搜索中，捕获结果具有明显的峰值，通过一定计算即可得到峰值处的时域序列位置与频域处的频偏大小。图8(b)为时域序列的小区搜索结果图，取频域最大频偏时的时域序列，两图表示的小区搜索结果相同，只是视角不同。

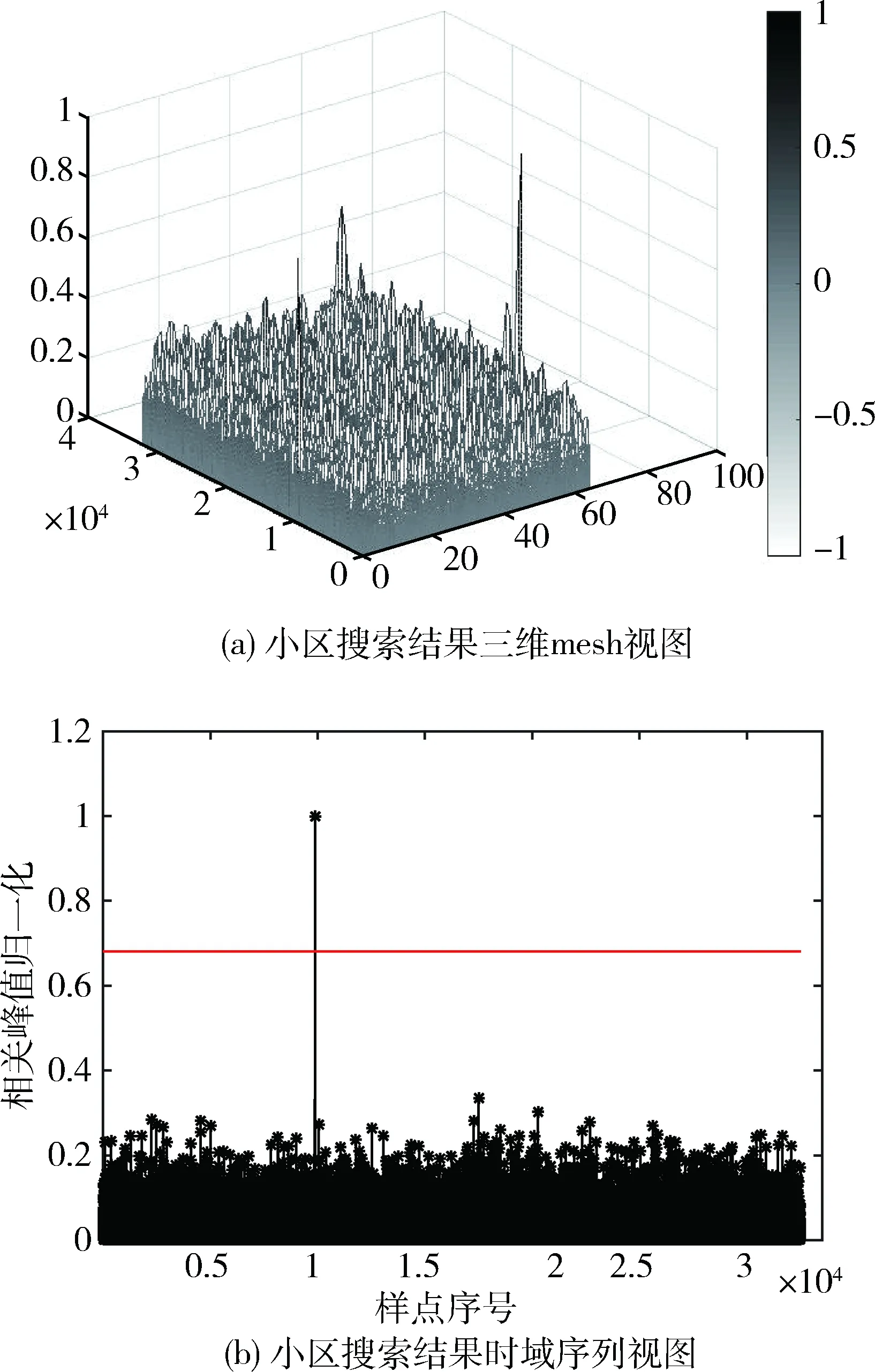
图8 载频号283小区搜索结果

从小区搜索结果可以看出，使用本文算法正确解调了基站空口信号，实现可靠快速捕获工作。

5 结束语

本文使用基于PMF-FFT的算法与自适应门限相结合的改进算法，实现了低信噪比下较大频偏的PN码的快速捕获，在捕获信号的同时获得频偏近似估计值。功率谱累积平均在一定程度上提高了较低信噪比下的捕获概率，而本文使用的自适应门限算法能够在保持虚警概率恒定的前提下，进一步提高较低信噪比下的捕获概率，在相关长度为256时，能够在静止环境下空口信号的捕获中取得较好效果，完成空口信号的正确解调。由于环境条件所限，未进行多径及高动态情形下的空口信号捕获，在高动态情形下，可以通过增加相关长度和功率谱累积次数来改善性能。

参考文献

[1] LIN J C. Noncoherent sequential PN code acquisition using sliding correlation for chip-asynchronous direct-sequence spread-spectrum communications[J]. IEEE Transactions on Communications, 2002, 50(4):664-676.

[2] SHEU C R, HUANG C C. A differential sliding correlation scheme for symbol timing detection in time domain synchronous OFDM systems[C]// Vehicular Technology Conference, 2009. IEEE, 2009:1-5.

[3] 赵志远, 陈树新, 华璐. 基于信噪比控制的滑动相关捕获法[J]. 科学技术与工程, 2013, 13(31):9386-9389.

[4] HUANG P, ZU B F. Performance analysis of PN code acquisition using fast fourier transform[C]// International Conference on Wireless Communications, Networking and Mobile Computing. IEEE, 2009:1-5.

[5] PING J, WU X, YAN J, et al. Modified zero-padding method for fast long PN-code acquisition[C]// Vehicular Technology Conference. IEEE, 2014:1-5.

[6] 曾婵, 李卫民, 毕波. 高动态GPS信号粗捕和精捕算法仿真实现[J]. 北京航空航天大学学报, 2017, 43(4):790-799.

[7] Li Chuanjun, Yang Shuxing, Ji Zhen. Performance analysis of fast GPS signal acquisition based on PMF and Window FFT[J]. Journal of Beijing Institute of Technology, 2012, 21(3): 291-297.

[8] CHANG L, ZHANG J, ZHU Y, et al. Analysis and optimization of PMF-FFT acquisition algorithm for high-dynamic GPS signal[C]//International Conference on Cybernetics and Intelligent Systems. IEEE, 2011:185-189.

[9] QI J, LUO F, SONG Q. Fast acquisition method of navigation receiver based on folded PMF-FFT[C]// Computing, Communications and It Applications Conference. IEEE, 2015:62-66.

[10] 罗海坤, 王永庆, 罗雨,等. PMF-FFT算法中码多普勒频率影响的分析及补偿[J]. 北京理工大学学报, 2013, 33(11):1176-1182.

[11] CHEN S, ZHANG T, HE D, et al. NLFM-DSS signal acquisition method based on DPT and PMF-FFT[C]// International Congress on Image and Signal Processing. IEEE, 2013:1444-1448.

[12] 杨秦彪, 王祖林, 黄勤,等. 高动态链路中折叠PMF-FFT快速捕获方法[J]. 系统工程与电子技术, 2016, 38(8):1723-1729.

[13] 黄明军, 王永民, 牛家红. 基于内插法的PMF-FFT系统多普勒频偏精度研究[J]. 应用科技, 2016, 43(4):46-49.

[14] 徐宁波, 宋荣荣. 基于PMF-FFT改进的捕获方法[J]. 无线电通信技术, 2014, 40(2):41-43.

[15] 孙大元, 王宪平. 基于PMF-FFT的高动态长伪码捕获实现[J]. 无线电工程, 2016, 46(8):65-69.

[16] 陈培, 王云, 陈杰. 短时相关和FFT相结合的伪码快速捕获算法[J]. 电子科技大学学报, 2009, 38(1):59-62.

[17] 刘燕丽, 张天骐, 苗圃,等. 部分相关与功率谱相结合的伪码快捕算法[J]. 测控技术, 2009, 28(11):14-18.

[18] 杜晓华, 张天骐, 庞统,等. 多径环境下直扩信号PN码捕获性能分析[J]. 计算机应用研究, 2010, 27(8):2913-2917.

[19] 高原, 张远见, 许鸿辉. 一种CDMA2000系统的PN码初始捕获算法[J]. 通信技术, 2010, 43(1):185-187.

[20] 赵敏, 杨涛, 胡波. 一种基于CDMA20001x EVDO微弱信号的捕获算法[J]. 太赫兹科学与电子信息学报, 2016, 14(6):878-884.