基于协同防御的水下拦截组合制导

， ,2， ,2 ，

(1.西北工业大学 航海学院,西安 710055； 2.西北工业大学 水下信息与控制重点实验室，西安 710055)3.西安建筑科技大学 机电工程学院，西安 710055)

0 引言

水下主要作战武器智能化程度的不断提高，使得当今乃至将来的海战进入一个武器对抗的时代。但由于海洋复杂环境的制约，基于协同对抗方面的研究主要集中在航空方面。文献[1]利用微分对策理论将目标、防御方和攻击方三者的对策问题转化为二体问题，体现了协同的概念，但是该制导律的推导需要解二点边值问题，且需较多的测量信息和估计信息，不利于工程实现。文献[2]基于微分对策理论，给出防御方与拦截方协同对抗攻击方的微分制导策略，但未考虑防御方的有效机动规避与实际应用性。文献[3]利用基于视线指令制导原理，应用逆系统控制方法设计目标飞行器反拦截协同制导策略，需要信息多、鲁棒性差。

随着传感器管理技术、水声通信技术、数据分发技术、水下多传感器信息融合技术的发展，各水下战斗单元的探测传感器进行联网管理，实现水下战场信息共享，为“水下协同防御”提供了必要条件。为此，鉴于我方舰艇进行鱼雷报警后，可捕获的来袭目标信息并不多，无法对来袭目标的机动策略进行精确预测，本文参考文献[1]和文献[3]思想，基于海战中来袭目标攻击我方舰艇、水下拦截器和我方舰艇协同防卫的特点，根据三方运动关系推导水下拦截器与我方舰艇协同对抗来袭目标的数学模型，利用伴随理论解决终端控制的最优制导问题方法，以终端脱靶量和控制能量为性能指标，分别求解用于最优导引与微分对策制导的零效脱靶量。通过仿真与性能分析，设计基于协同防御的组合制导律。

1 问题描述与建模

海战中对抗三方的相对运动关系如图1所示，设本艇S在W0点的航向Cs和航速Vs，发现距离RSR的L0点航速为VR的来袭目标R，经作战决策后，发射航速为VA的水下拦截器A进行拦截。

图1 制导末端三方的相对运动关系

由图1可知来袭目标与水下拦截器之间的运动关系为：

(1)

同理可得来袭目标与舰艇，水下拦截器与舰艇之间的运动关系。基于视线角制导原理对水下拦截器与来袭目标的相对运动关系式(1)进行求导得：

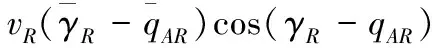
(2)

(3)

其中：aSplos为垂直于舰艇与来袭目标视线角方向的瞬时舰艇加速度。aRplos为垂直与水下拦截器与来袭目标视线角方向的瞬时鱼雷加速度。设aSx，aSy，aRx，aRy分别为舰艇与来袭目标加速度在参考坐标方向的分量。由图1运动方位可知：

(4)

由此可知：

aSplos=aSxsinqSR+aSycosqSR

aRplos=-aRxsinqAR-aRycosqAR

(5)

由于在制导初始对准良好的情况下，三方都可近似为线性动态特性的质点，并可沿初始视线方向进行线性化[5]，且来袭目标与水下拦截器的初始目标视线位于“碰撞三角形”附近，整个飞行过程相对“碰撞三角形”偏离不大，因此可通过鱼雷命中条件[6]和各自作战目的求解对策三方的相互航向角约束关系：

ηRS=arcsin(VSsin(qSR-γs)/VR)

γR=π+qSR+ηRS

ηAR=arcsin(VRsin(γR-qAR)/VS)

γA=qAR-ηAR

(6)

假设对策三方具有线性控制系统动态，但不对其阶次进行约束。设水下拦截器具有nA阶控制系统(自动驾驶仪)动态，且状态空间实现为{AA,bA,cA,dA}，其传递函数表示为:

GA(s)=cA(sI-AA)-1bA+dA

(7)

定义中间状态变量xA∈RnA，则进一步表示为：

(8)

其中：uAc为水下拦截器的控制命令，同理，可对来袭目标和舰艇的控制系统动态进行相应假设，状态空间实现分别为{AR,bR,cR,dR}和{As,bs,cs,ds}，传递函数可表示为GR(s)和GS(s)，相应的控制命令为uRc和uSc。

由于海战中对抗的实质是“攻”与“防”双方在战场态势空间上的博弈问题，即舰艇规避来袭目标的攻击的同时促进水下拦截器对来袭目标的成功拦截，来袭目标攻击舰艇的同时规避水下拦截器，水下拦截器促进舰艇逃逸的同时拦截来袭目标。为提高我方舰艇的防御能力，当舰艇接收到来袭目标预警后，应立即启动防御系统。考虑到复杂海洋环境对信息传递的干扰作用，在舰艇无法通过最优机动成功摆脱来袭目标的情况下，对我方舰艇实施“匀速+旋回+加速”的机动规避。即舰艇发现目标后，保持匀速航行并发射水下拦截器，然后以最快角速度旋回至将来袭目标甩到我舰舰尾舷角120°～160°范围后[7]，进行加速直航，这样，有效确保了拦截器发射信息的准确性。

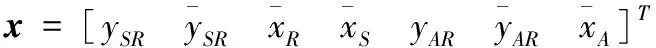
(9)

其中：

ui为相应的控制命令，ui<1,i={Ac,Sc,Rc}；且zi=aimax/ui。

由于运算中将三方当作具有多个控制的单个对象看待，针对存在的两组不同对抗，可将航行时间表示为tfSR=RSR0/VcSR0与tfAR=RAR0/VcAR0，RSR0，RAR0分别为来袭目标与我方舰艇和水下拦截器与来袭目标的初始距离，VcSR0，VcAR0为相对应的接近航速。要实现成功防御的目的，要求水下拦截器先于来袭目标完成任务，即Δt=tfSR-tfAR>0。

2 制导律的设计

根据我方舰艇、来袭目标、水下拦截器三方作战特点及追逃关系，可将三者对策分解为两两之间的对策与综合。其中水下拦截器拦截来袭目标的反馈控制回路为：

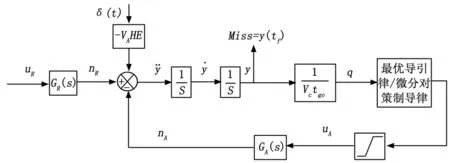
图2 水下拦截器拦截来袭目标的控制系统模型

同理，可推导来袭目标攻击我方舰艇的控制系统模型，其中我方舰艇为两组拦截运动的公有项。

根据反馈控制原理，控制系统的主要目标是寻求最佳的控制量u使拦截方与目标方的终端脱靶量最小和控制拦截方完成拦截所需的机动能量[8]。为达到这两目标，对终端脱靶量和控制函数加以性能指标约束。则线性二次性能指标表示为：

(10)

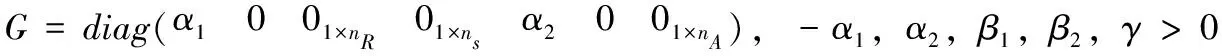
结合系统状态方程构造哈密顿函数：

(11)

采用伴随原理，利用终端条件x(tf)反向求解当前状态，可得：

BSuSc*+BRuRc*]dτ

(12)

其中：Φ(tf,t)为状态转移矩阵，tf i= tf SR,tf AR。

由于逐步推导求x(tf)的表达式求取最优解的过程比较复杂，引入具有预测性能的零效脱靶量。零效脱靶量的物理意义为拦截器从当前时刻到制导结束不再输出制导指令，而目标按以前的机动方式运动，到制导结束时的脱靶量大小[9]。假设符号j={SR,AR}分别表示来袭目标与我方舰艇、水下拦截器与来袭目标的相对关系；k={S,R}分别表示我方舰艇与来袭目标；l={R,A}分别表示来袭目标与水下拦截器。则由(12)可求得微分对策制导律的零效脱靶量:

(13)

其中：tgoj=tfj-t为待航行时间，。

同理可求得最优控制下的脱靶量为：

τl2ψ(0,tgoj/τl) ildeal

(14)

(15)

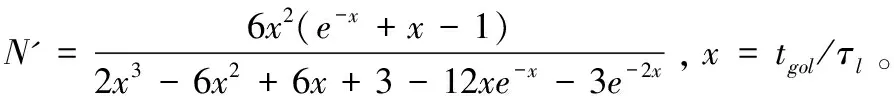
uDG=amaxsign(zDG)

(13)

3 仿真及性能分析

结合图1运动关系，对上述所推导的制导律进行应用仿真及性能分析。针对来袭目标机动策略无法预知，假定来袭目标分别采用最优导引与微分制导策略实施攻击，分析比较当水下拦截器实施微分对策制导与最优制导策略时，水下拦截器的拦截效果和舰艇的防御能力。

假设对策三方都具有一阶控制系统，首先根据水下拦截器捕获目标的条件，假设水下拦截器的搜索扇面角为45°，选X轴为我方舰艇的初始航向，且我方舰艇初始位置为(0,0)，来袭目标初始位置(800,1 000)，水下拦截器的初始位置(0,0)，我方舰艇速度：vS=10 m/s，来袭目标速度：vR=20 m/s，水下拦截器速度为：vA=25 m/s；一阶系统时间常数分别为：τR=0.2 s，τA=0.08 s，τS=0.2 s，来袭目标与水下拦截器的初始偏航角都为0。我方舰艇发射水下拦截器后，经短暂匀速直航，然后再采用“旋回+加速”的机动样式进规避。假定水下拦截器毁伤最大半径为20 m。在水下拦截器成功拦截同时舰艇至少规避到拦截点100 m外，三方对策仿真曲线和结果如图3和表1所示。

图3 来袭雷不同导引策略的三方对策航迹

由图3三方对策航迹可看出，舰艇发射水下拦截器后，以“旋转+加速”方式将鱼雷摆脱在舷尾，增大了鱼雷攻击距离，提高了生存概率。针对不同制导策略的来袭目标，在制导前期，水下拦截器采用最优导引策略的弹道航迹比微分对策导引的平滑，且快速响应性好，便于水下拦截器根据舰船的协同信息及时调整航行弹道。但在制导后期，其响应速度慢于微分对策制导曲线，不利于对机动性较强的来袭目标实施快速攻击。对应的仿真结果为表1。

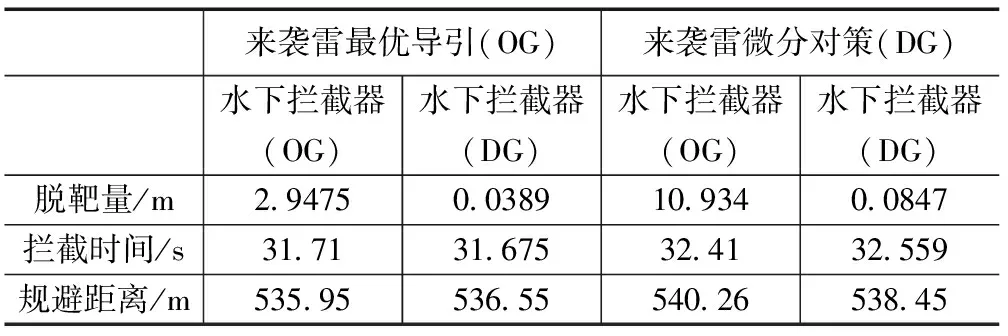
表1 三方对策仿真结果

由表1仿真结果可知，针对不同策略的来袭目标，水下拦截器采用微分对策制导进行拦截时，终端脱靶量小明显小于最优导引的制导结果，且舰艇可规避到相对较远的距离，提高了舰船的生存概率。为验证微分对策制导的性能优势，对实施拦截过程中的零效脱靶量和不同初始距离的终端脱靶量进行仿真，结果如图4和图5所示。

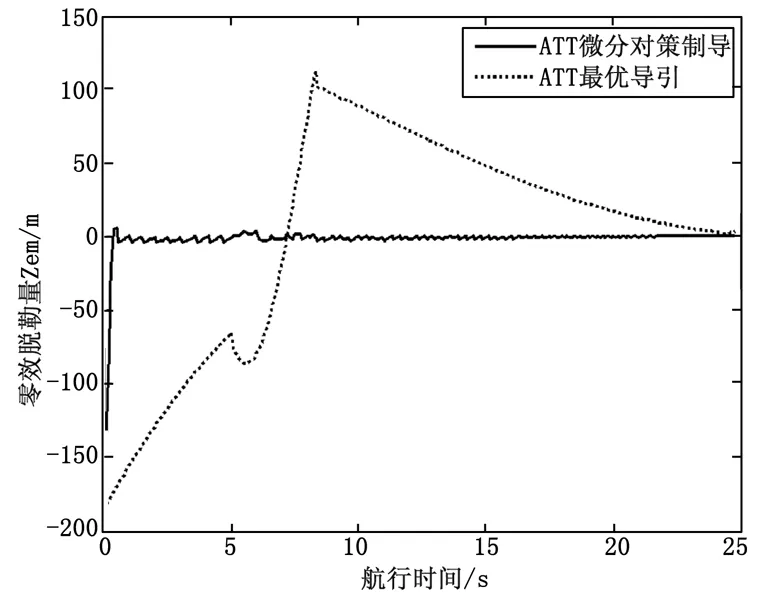
图4 水下拦截器不同制导方式的零效脱靶量

由图4可知，水下拦截器采用微分对策制导进行拦截时，零效脱靶量快速逼近0位，并在0位微小波动，而采用最优导引进行拦截时，零效脱靶量需经较长时间振荡变化才能逼近0位。

图5 不同初始距离下不同制导方式的末端脱靶量

由图5可知，采用微分对策拦截不同制导策略的来袭目标时，初始距离变化对终端脱靶量影响不大。而采用最优导引时，当初始距离大于1 600 m时，终端脱靶量数值曲线增速较快，不利于拦截。虽在距离小于1 000 m，终端脱靶量有快速变小趋势，但仍次于微分对策制导。因此，实施近距离攻击时微分对策制导很具优势。对不同制导策略下水下拦截器的控制命令进行仿真分析，如图6所示。

图6 水下拦截器不同策略制导加速度曲线

可见，采用最优导引时，在制导末端要求水下拦截器具有很强的机动性能，控制能量消耗较大，且会增加失速的危险，不利于控制。采用微分对策时，由于该类型制导律具有“bang-bang”结构，能够满足系统快速性的要求，实现阶跃过程最小化，较大的提高水下拦截器制导精度，缩短拦截时间。但在实际控制过程中，控制量在极值之间的快速切换时不可避免地存在时间滞后，造成系统抖动，且频繁切换控制量会造成执行机构严重磨损，不利于工程实现[9]。

基于微分对策制导与最优导引在制导不同阶段的优势，将最优导引与微分对策制导组合对水下拦截器进行导引控制。仿真结果为：当水下拦截器采用组合制导拦截采用最优导引的来袭目标时，终端脱靶量为：0.788；拦截时间为：24.83 s；舰艇距拦截点距离为:894.19 m。当来袭目标采用微分对策制导时，脱靶量为：1.106 7；拦截时间为：23.899 s；舰艇距拦截点距离为：897.07 m。与表1数据进行对比，组合对策制导拦截效果优于纯最优导引，稍次于纯微分对策制导。组合对策制导加速度变化曲线如图7。

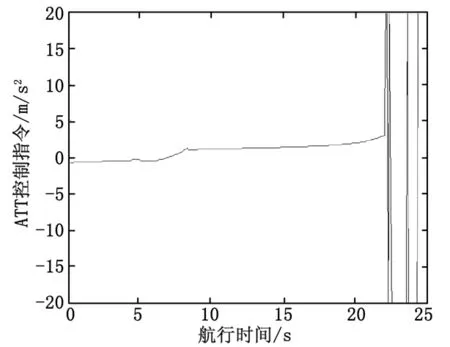
图7 水下拦截器组合对策制导加速度变化

由图7可知采用组合制导，既降低了最优导引在制导末端对水下拦截器的机动性能要求，增强了系统的稳定性，也将“bang-bang”机动切换频率缩减了80%，在保证系统优良的动态特性同时，有效降低控制命令在极值之间的切换频率，提高了机构的使用寿命,极大的增强了工程应用性。

4 结论

为充分提高我方舰艇在海战中的防御能力，针对目标机动方式的无法预测性，研究了基于协同防御特性的反鱼雷拦截组合制导问题。

通过水下拦截器制导早期舰艇机动规避方式的设计，利用视线制导指令得出的加速度与角度约束，建立水下拦截器与我方舰艇的协同对抗来袭目标的作战模型，有效降低了距离对信息协同的延迟影响，使水下拦截器实现了制导弹道航迹的实时调整，为制导末端精确、快速的拦截提供保障。

在控制律推导环节，引入零效脱靶量，应用伴随理论解决终端控制问题方法，避免了微分制导律推导过程中求解二点边值的复杂过程，可适用于三方任意阶控制的情形，便于工程实现。

通过对不同机动方式来袭目标的拦截仿真及性能分析，在保证拦截效果前提下，从控制指令的性能及工程应用合理性出发，对组合制导优势进行了分析。该组合控制克服了单一制导的不足，同时具有优良的动态特性和稳定特性，具有强的鲁棒性，可实现对来袭目标的有效拦截。

参考文献:

[1]陈春玉.反鱼雷技术[M].北京：国防工业出版社，2006.

[2]Rusnak I．Guidance laws in defense against missile[A]. Proceedings of the IEEE 25th Convention of Electrical and Electronics Engineers[C]. Israel：IEEE Press，2008：90-94．

[3]花文华.寻的导弹微分对策末制导方法研究[D]. 哈尔滨:哈尔滨工业大学,2011.

[4]肖增博，雷虎民.目标飞行器反拦截协同制导策略[J].兵工学报,2011,12(32):1486-1492.

[5]李运迁.大气层内拦截弹制导控制及一体化研究[D].哈尔滨:哈尔滨工业大学，2011,6.

[6]孟庆玉，张静远.鱼雷作战效能分析[M]. 北京：国防工业出版社，2003.

[7]贾 跃，宋保维.水面舰船对声自导鱼雷防御机动方法研究[J].火力与指挥控制,2009，34(1):45-50.

[8]徐德民.鱼雷自动控制系统[M].西安：西北工业大学出版社,2001.

[9]李运迁，齐乃明.基于零控脱靶量的大气层内拦截弹制导律[J].宇航学报.2010，7(31):1768-1774.

[10]周 荻.寻的导弹新型导引规律[M]. 北京：国防工业出版社，2002.