随机编码超表面的RCS缩减特性研究

杨家稷，程用志，龚荣洲

（1. 华中科技大学 光学与电子信息学院，湖北 武汉 430074；2. 武汉科技大学 信息科学与工程学院，湖北武汉 430081）

超表面作为一种人工周期性或非周期性结构表面，由亚波长尺度的基本单元组成。由于其能够操控电磁波，可以广泛地应用于雷达隐身领域[1-4]。对于雷达隐身技术，主要通过改变雷达回波特征信号，来减小物体被探测概率，而雷达散射截面积（Radar Cross Section，RCS）就是衡量目标雷达回波能力的一个重要物理量，通过设计合适结构的超表面能够实现RCS的有效缩减[5-8]。

近些年来，低RCS特性人工磁导体超表面引起了研究人员的极大关注[9-12]。该类超表面将入射电磁波反射到后向空间，而不是转换为热能，极大地降低了雷达波被红外装置探测的可能性[13-16]。作为一种新型超表面，相位梯度超表面在面内方向引入人工波矢，更加自由地调控反射波波束的传播方向，可设计多个基本单元，在宽频带范围内实现稳定相位差，广泛应用于宽频带的RCS缩减特性研究[17-20]。2011年，哈佛大学Capasso等基于相位梯度超表面的设想，首先提出“广义斯涅尔定律”，随后设计了基于V型阵列结构的相位梯度超表面，实现对散射电磁波的相位调控[21-23]。复旦大学周磊等设计的相位梯度超表面能使入射波转变为表面波，且转化效率非常高，之后将表面波沿平面方向用探针导出，验证了表面波的存在[24-25]。2014年，东南大学崔铁军等[26-28]提出超编码理论，通过调控各单元的相位，使其产生稳定的相位差，编码超表面能将电磁波的能量散射到各个方向。当超单元随机排列时，入射波被无规则地反射回自由空间，因此每个方向波束的散射能量很小，可以实现RCS的有效缩减，同时所设计编码超表面具有极化不敏感的特点，能够实现各个极化方向入射电磁波的RCS缩减[29-34]。

金属分割线结构具有模型结构简单、几何参数易于调节的优点，被广泛运用于超材料或超表面的设计中。本文基于漫反射和随机编码理论设计三种随机编码超表面，着重讨论超单元排布方式对 RCS的缩减特性。所设计编码超表面呈现出宽频带、极化不敏感、宽角度入射的特性。仿真和实验表明，对于垂直入射的x/y-极化波，超表面在6～14 GHz频段内存在6 GHz带宽的RCS缩减大于10 dB. 同时，在斜入射的情况下，RCS缩减仍有较好的效果。

1 随机编码超表面设计

1.1 随机编码理论

本文基于类似反射天线阵的原理，设计一系列不同组合方式的随机编码超表面。通过对超编码排布方式的设计，使入射波发生漫反射，根据能量守恒定律，减少单个方向的能量散射，从而达到全方向RCS缩减的目的。

假设该表面由N×N个阵元组成，每个阵元都是由“0”或“1”这两个基本单元组成，同时每个单元的散射相位为两单元分别对应0°和180°。在电磁波垂直入射的情况下，该表面的远场散射可以表示为：

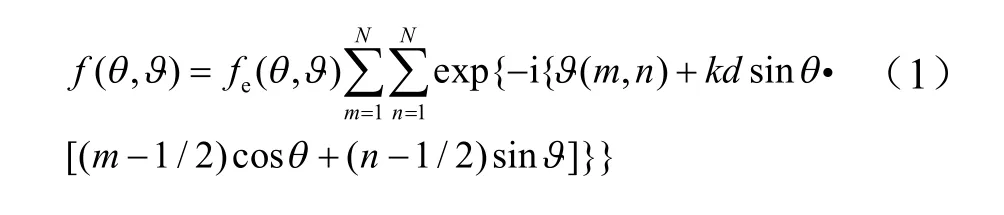
式中：θ和ϑ分别为入射角和方位角；k=2π/λ；d为单元之间的距离；fe（θ,ϑ）为单个阵元的辐射强度。方向图函数可以表示为：

由于“0”和“1”这两个基本单元散射相位差为±180°，从而形成180°的相位梯度，其散射特性相互抵消，fe（θ,ϑ）的幅值特性基本为0。从（1）、（2）两式可以看出，随着编码阵元排列方式的改变，超表面远场散射特性也会随之改变。

通过简单地旋转图形，实现“0”和“1”基本单元交叉极化反射相位差为 180°的特性，避免图形尺寸设计的改变，更简洁有效地对超表面进行不同方式的排布。提出一种随机编码排布运算，使“0”单元和“1”单元在矩阵中的数目一致，设计2bit编码超表面，如图1所示，带入MATLAB中计算。“0”单元和“1”单元被高自由度地分布到矩阵中，入射波发生漫反射，电磁波被均匀地散射到自由空间，使得不同编码序列的RCS缩减曲线完全一致。两基本单元的数目相同，同极化反射相位重合，交叉极化反射波相位相差 180°，其散射场的交叉极化分量被有效地抵消，因此该运算方式得到的超表面具有更好的 RCS缩减效果。

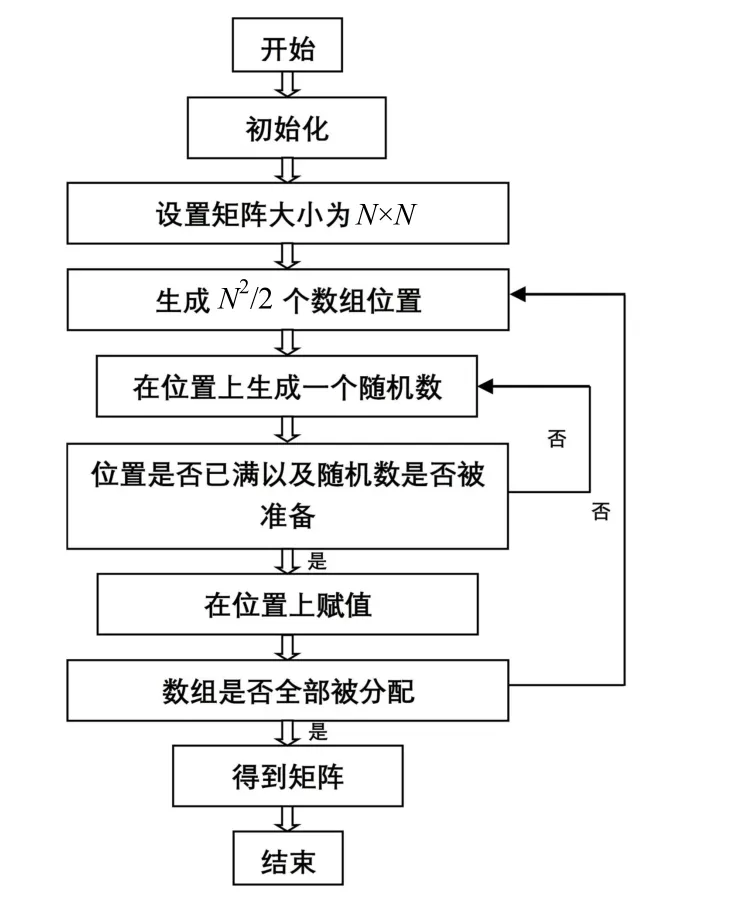
图1 随机排布运算流程图Fig.1 Random arrangement flow chart

随机编码模式Mrandom可以定义为如下的函数形式：

式中： r and（ 2i）,o ne s（ 2N-i） 表示分块矩阵的数目为2i× 2i，每个分块矩阵由2N-i× 2N-i个相同随机数组成，随机数开区间范围为（0, 1）。通过MATLAB进行运算，可调控超表面随机编码模式的获取步骤如下：首先，统计这些范围在（1,N）的不同随机矩阵数目；其次，分别计算其模式数；最终，将连续的随机数（0和1）带入离散的二进制编码“0”和“1”，并通过运算流程图进行计算，得到随机编码矩阵。基于仿真优化结果，同时方便后续样板的制备和测量，选取i=8，N–i=5，因此，该超表面由8个超单元组成，每个超单元包含5×5个基本单元，最终编码超表面的个数为40×40。

1.2 随机编码排布方式

本文设计如图2（a）所示基于金属分割线结构的超表面基本单元，设其为“0”单元。将上层金属分割线沿逆时针旋转90°，得到图2（b）所示超表面单元结构，设其为“1”单元。整个单元分为三层，单元周期p= 10 mm，上层为金属分割线结构铜膜，长宽分别为l= 10 mm，w= 1.6 mm，与y轴夹角为45°；中间层介质基板FR4的厚度为3.5 mm，介电常数为4.3，损耗角正切为0.025；背板为铜膜，厚度与上层铜膜都为0.035 mm。

图2（c）为极化转换效率曲线，可以看出，x-极化波和y-极化波在6～14 GHz频段范围内的线极化转换效率高达90%，且在谐振频点处达到99%。图2（d）给出了“0”和“1”单元这两个结构的交叉极化相位，结果表明，在整个4～16 GHz频段范围内，超表面相位梯度为 180°。因此，利用金属分割线结构单元“0”和“1”工作状态的交叉极化反射相位差为±180°的特点，基于随机编码理论，设计出缩减RCS的随机编码超表面。

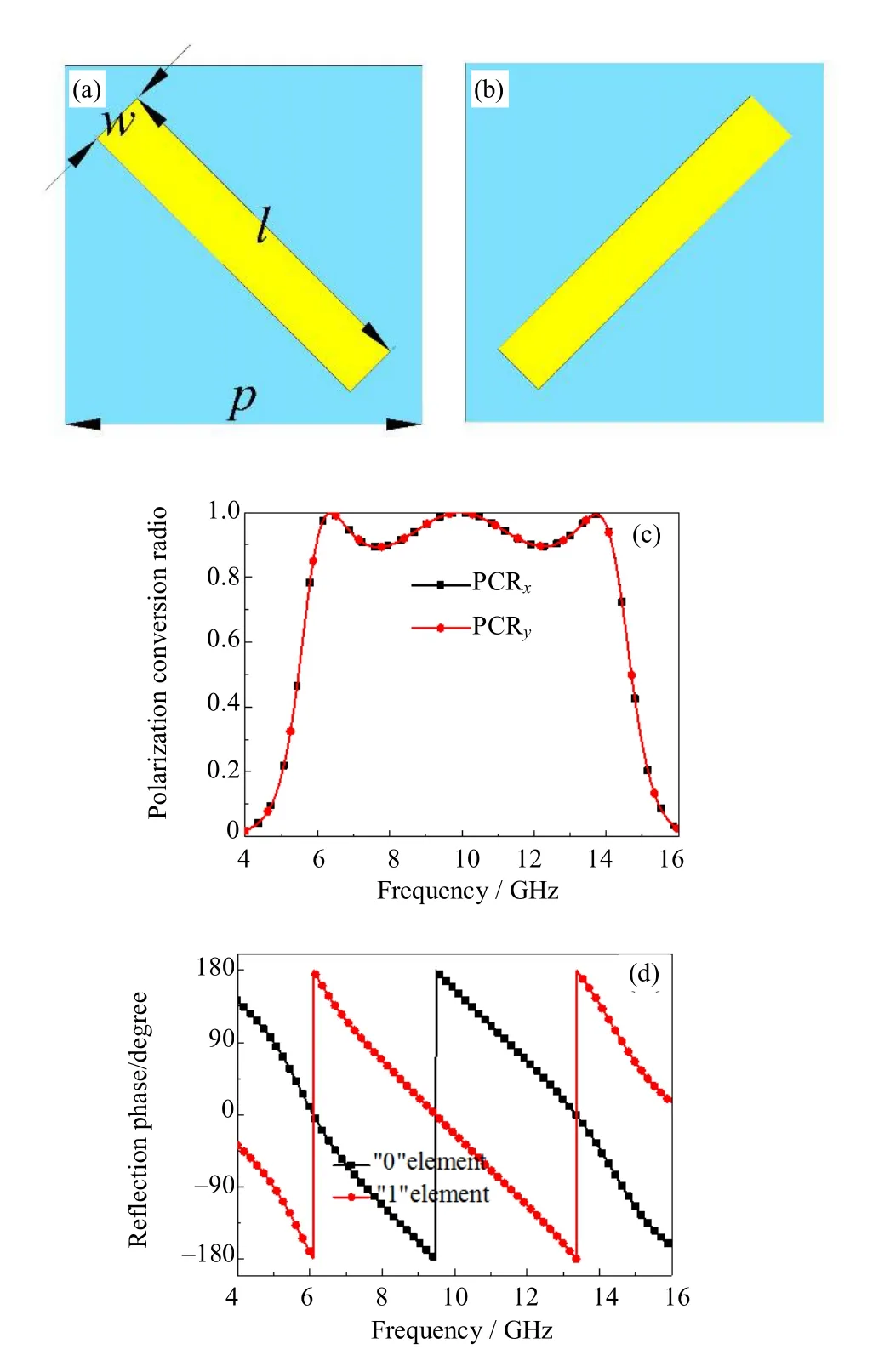
图2 （a）基本单元“0”；（b）基本单元“1”；（c）x-极化波和y-极化波的线极化转换率；（d）“0”单元和“1”单元的反射相位Fig.2 (a) Base unit “0”; (b) Base unit “1”; (c) The linear polarization conversion ratio of x- and y-polarized wave; (d)Reflected phase of “0” unit and “1” unit

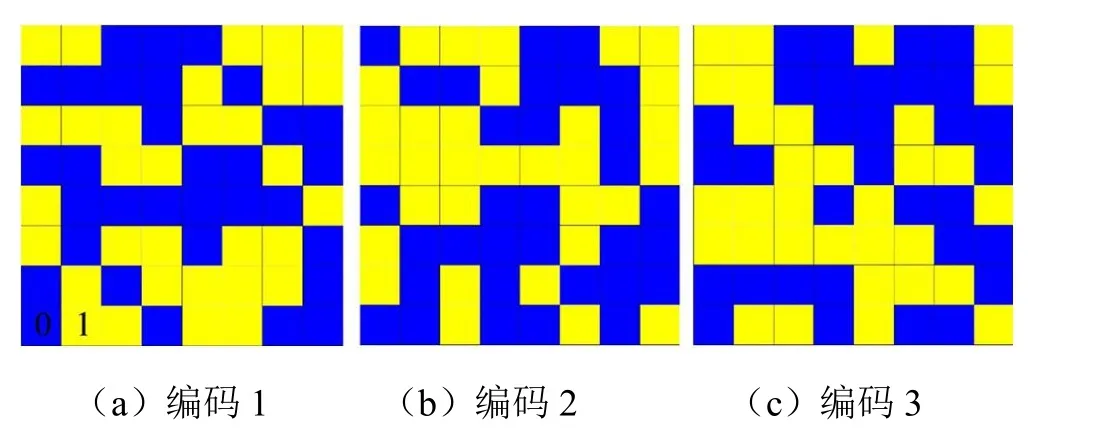
图3 三种随机编码超表面的排布示意图Fig.3 Arrangements of three random coding metasurface

为了探索随机编码超表面的RCS缩减特性，设计三种不同的随机编码序列，图3为三种随机编码超表面的编码示意图。通过调控超表面的编码方式，改变能量散射方向，使电磁波发生漫反射，从而达到缩减单个方向RCS的目的。图4为10 GHz时三种随机编码超表面的远场散射特性图，可以看出三种随机编码序列的能量散射都向四周扩散，单个方向散射能力较弱，由此表明这些随机编码超表面具有良好的RCS缩减特性。

2 仿真与实验结果

2.1 随机编码超表面的仿真与分析

图5 （a）不同超单元组合下编码3的RCS缩减；（b）编码3超表面x-和y-极化波入射时的RCS缩减Fig.5 (a) RCS reduction of coding 3 at different supercell combinations; (b) RCS reduction of coding 3 at x- and y-polarized waves incidence

利用电磁仿真软件CST MICROWAVE STUDIO频域求解器，对如图3所示的编码3进行数值模拟仿真，将n×n的基本单元作为超单元，设计基本单元为 1×1，2×2，3×3，5×5的超单元，探索超单元组合对RCS的缩减特性的影响。图5（a）为在不同超单元组合下编码3的RCS缩减。由图可以看出随着超单元中基本单元个数的增加，RCS缩减增大，且向低频移动。1×1超单元的RCS缩减在全频段皆较小，基本在5 dB以上；2×2超单元的RCS缩减整体增大，基本在10 dB以上；5×5超单元相对3×3和2×2超单元的RCS缩减整体向低频方向偏移，且数值大小趋于稳定，具有较好的RCS缩减特性。之后，随着基本单元个数的增加，RCS缩减基本不变，且单元数的增多会增大样板的尺寸，不便于测量。为了满足实验室测量条件，与已有的400 mm×400 mm金属板大小匹配，采用5×5的基本单元作为一个超单元，设计多个随机编码序列来探索超表面对RCS的缩减特性。

仿真得到编码3超表面在x-极化波和y-极化波入射时的RCS缩减，如图5（b）所示，不同极化波入射时RCS缩减曲线基本一致，说明该超表面具有极化不敏感特性。另外，超表面在6～14 GHz宽频带范围内存在6 GHz带宽的RCS缩减大于10 dB，在9.5～10.5 GHz频段内大于20 dB，在10 GHz处达到最大值27.5 dB。接下来将着重研究随机编码超表面的RCS缩减特性。

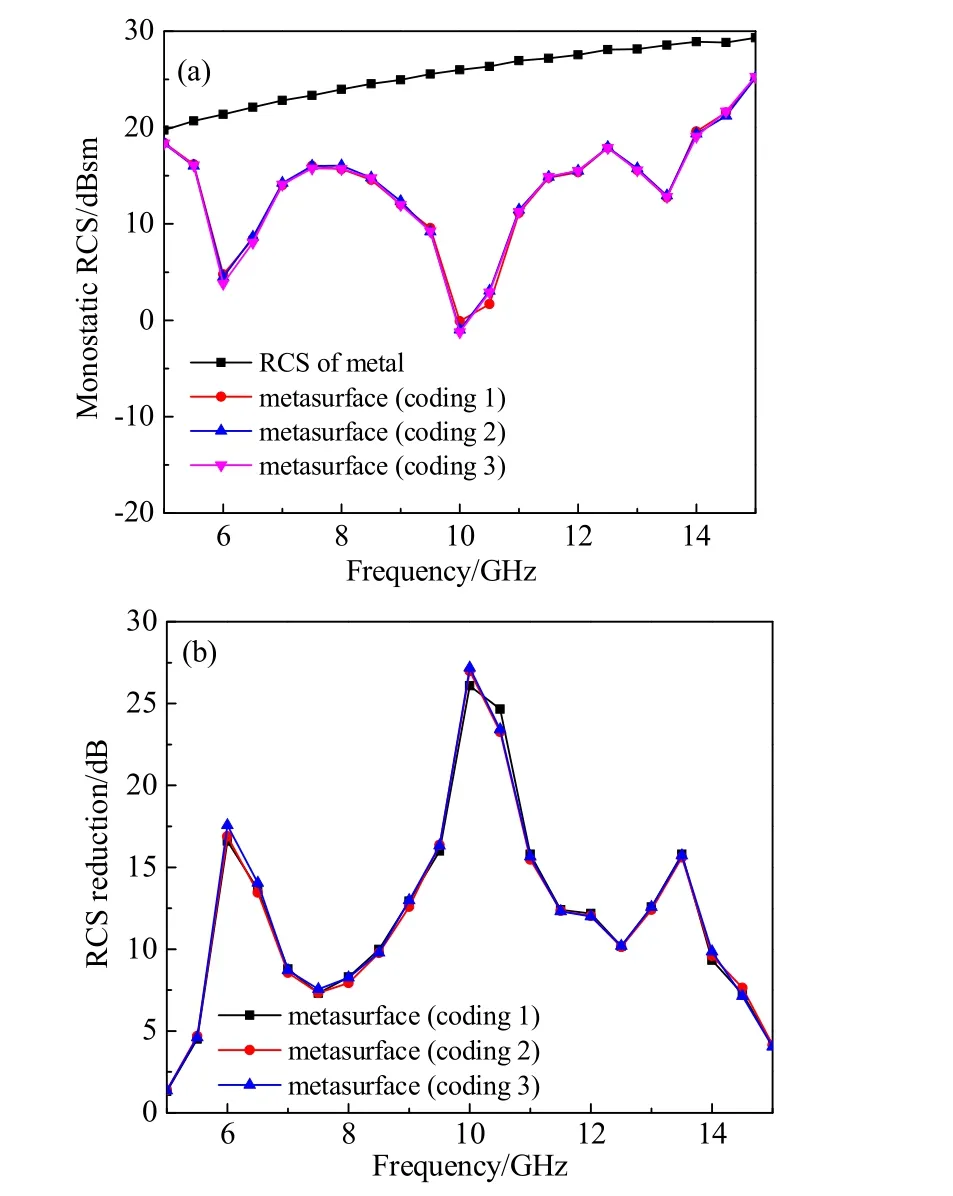
图6 垂直入射时各排布方式的（a）单站RCS；（b）RCS缩减Fig.6 Simulated results of a series of random coding metasurfaces: (a) monostatic RCS of the different coding metasurfaces and metal; (b) RCS reduction of the different coding metasurface

对图3所示的三种随机编码超表面进行数值模拟仿真，图6为垂直入射条件下各排布方式的单站RCS与RCS缩减，可以看出超表面均可在宽频带范围实现RCS缩减，不同编码序列的仿真结果具备高度一致性，能有效地减少使用同一算法时编码不同产生的仿真误差。同时，该类随机编码超表面的散射特性基本一致，不随编码方式的不同而改变，其能量向四周散射，大幅提升RCS缩减。该结果进一步验证了随机编码理论的可行性。

进一步讨论随机编码超表面的RCS缩减特性，仿真得到如图7所示垂直入射时xoz平面的散射方向图，这里将5，7，10，11，13和15 GHz时编码3与同等面积金属板的散射特性作对比。根据能量守恒定律，增强旁瓣的散射能量能够抑制主瓣能量，从而实现垂直方向的RCS缩减。由方向图可以看出金属表面在全波段都有一个垂直方向的强主瓣，图7（a）和（f）可以看出频率为5，15 GHz时，相对金属表面，超表面对主瓣几乎没有抑制作用；图7（b）和（e）所示，频率为7，13 GHz时，超表面相对金属表面在主瓣方向有一定的抑制作用；图7（c）和（d）表明频率为10，11 GHz时超表面对主瓣有明显的抑制作用。综合上述结果可知，越靠近基本单元的中心频率，RCS缩减效果越明显。极化转化超表面可实现宽频带的RCS缩减，同时对散射场进行动态调节。

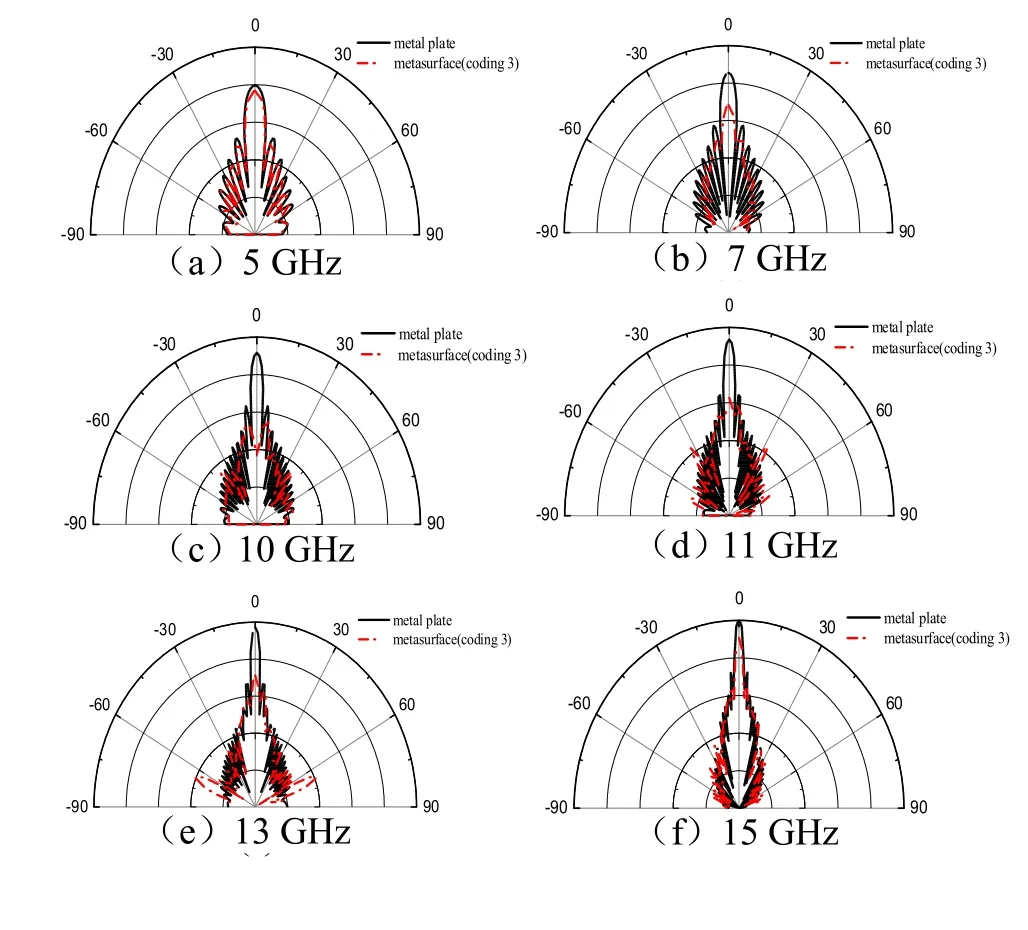
图7 不同频率下编码3和同等面积金属板的散射特性对比图Fig.7 Scattering characteristics of coding 3 and metal plates at different frequency

2.2 随机编码超表面的测试与分析

制备三种随机编码超表面样板，并在微波暗室中进行测量。其面积为400 mm×400 mm，厚度为3.57 mm，每块样板由8×8的超单元组成，每个超单元由5×5的基本单元“0”或“1”组成，样板如图8所示，上层为0.035 mm厚的铜膜，中间层为3.5 mm的FR4基板，下层为0.035 mm的金属板。采用自由空间法对三块样板进行测试，将样品通过夹具固定在泡沫塔上，在远处将发射和接收喇叭固定在泡沫塔前方同一水平高度，将Agilent Technologies N5244A矢量分析仪两端口的接线连在喇叭天线上，测量样板的RCS。

图8 3种随机编码超表面样板Fig.8 Three types of random coding metasurface templates

如图9所示给出三种随机编码超表面在x-极化波和y-极化波垂直入射下的测试反射率。对于编码1，如图9（a）所示，可以看出x-极化波和y-极化波入射条件下反射率曲线基本一致，反射率（x-极化入射和y-极化入射）在5.5～6.5 GHz范围内小于–10 dB，在6.5～8.3 GHz存在一个回升的峰，反射率大于–10 dB，在8.3～13.2 GHz范围内反射率重新回到–10 dB以下。就编码2而言，如图9（b）所示，8 GHz之前曲线基本相同，8 GHz之后，y-极化波入射时反射率存在一个回升的峰，因此x-极化波入射具有更好的效果，但由于测量误差以及样板的加工误差，整体上看，两曲线基本保持一致性。对于编码3，如图9（c）所示，x-极化波入射和y-极化波入射的反射率曲线完全重合，保持高度的一致性，在5.5～6.5 GHz范围内反射率小于–10 dB，当频带为6.5～8.5 GHz范围时，反射效果增强，反射率大于–10 dB，在8.5～13.2 GHz反射率重新降到–10 dB以下。总的来说，通过随机编码运算得到的编码序列，都具备极化不敏感的特性，且测试样板也具有较好的反射特性。

图10给出了测试样板在斜入射情况下的 RCS缩减，可以看出6～14 GHz范围内存在6 GHz带宽的RCS缩减大于10 dB。入射角为15°和30°时，相较垂直入射，RCS缩减效果反而有略微的增强。斜入射RCS缩减效果显著提升，该超表面具有较好的宽角度入射特性。对这三种随机编码超表面，不同入射角对应的曲线略有不同，但基本保持一致，可以认为随机编码超表面的斜入射RCS缩减也具备一致性。

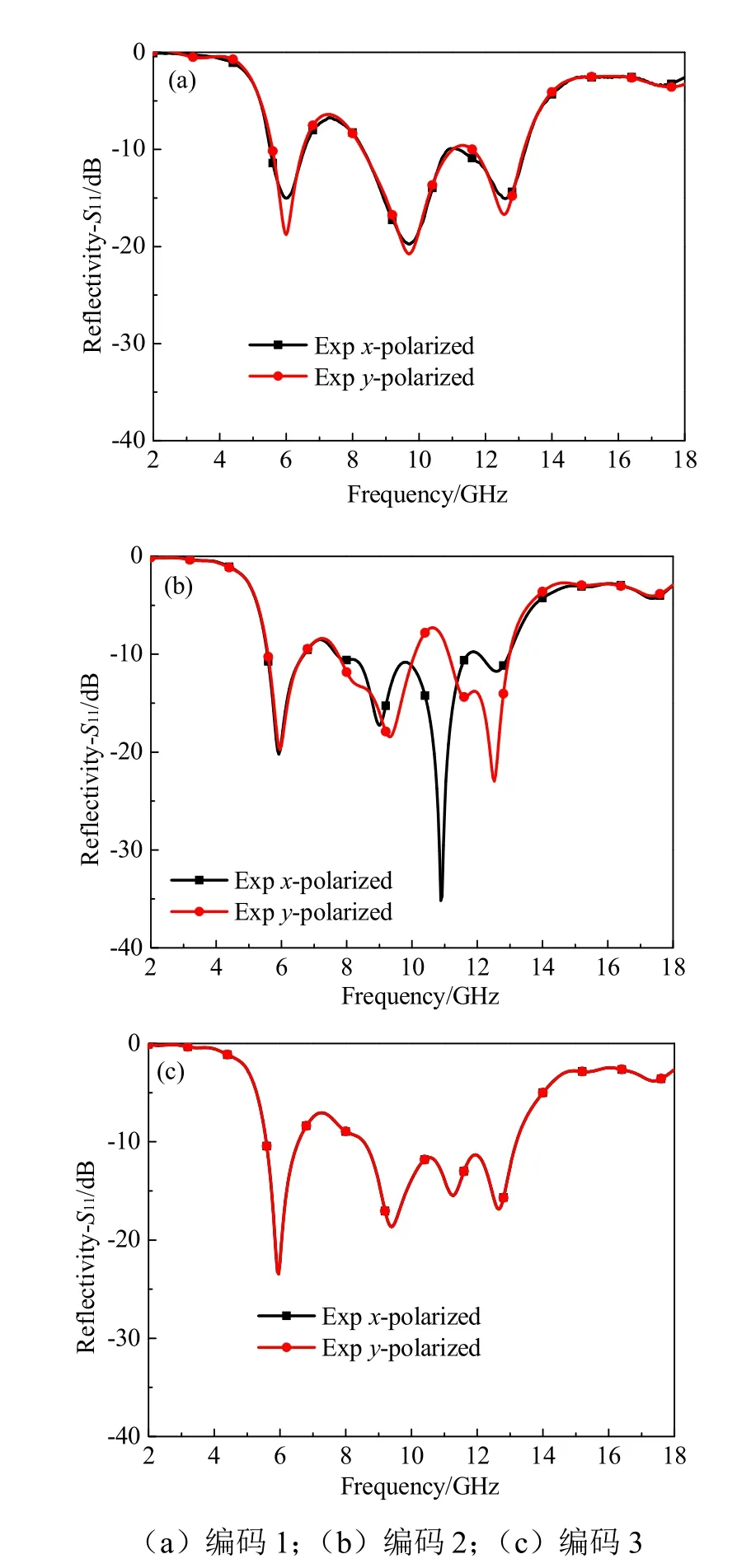
图9 x-极化波和y-极化波入射条件下的反射率曲线Fig.9 Reflectivity curves at x-polarized and y-polarized wave incidence

3 总结

本文基于超编码理论，设计三种随机编码超表面，探索其RCS缩减机制。讨论不同超单元组合下编码超表面对RCS缩减的影响，以及不同排布方式对RCS的缩减特性。对超表面进行仿真，得出垂直入射时的RCS缩减图和散射方向图，探讨随机编码序列中的能量散射方向。仿真和实验表明，对于垂直入射的x/y-极化波，在6～14 GHz宽频带范围内，超表面的反射率基本小于–10 dB，存在6 GHz带宽的RCS缩减大于10 dB，编码超表面呈现出宽频带RCS缩减特性。斜入射情况下，RCS缩减仍有较好的效果，与垂直入射时的曲线基本一致，具备宽角度入射RCS缩减特性。该超表面的提出为隐身材料的设计提供了全新的指导。

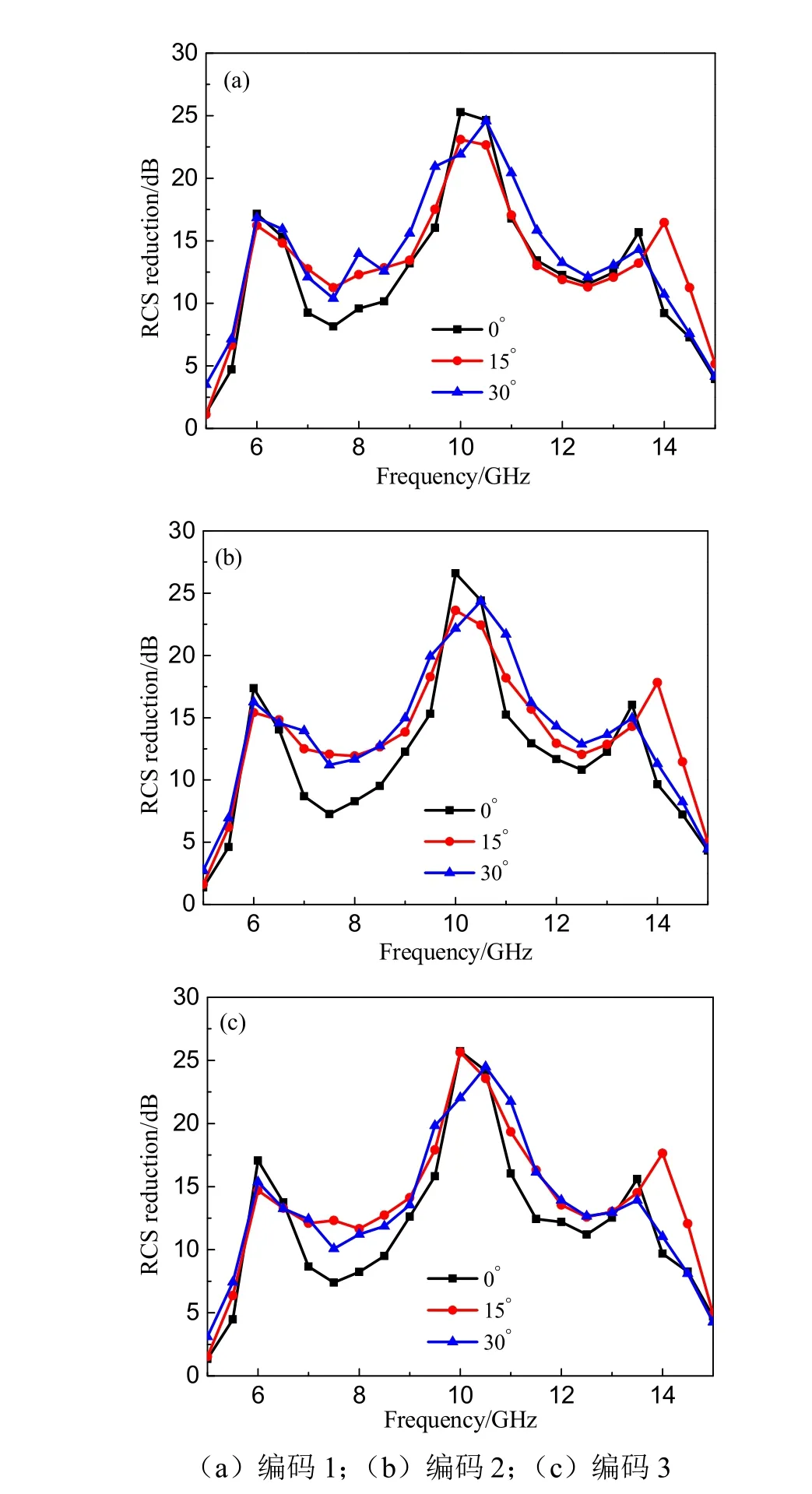
图10 垂直入射和入射角为15°，30°时的测试RCS缩减Fig.10 Measured RCS reduction of samples under oblique incidence of 15°, 30°

参考文献：

[1]PENDRY J B, SCHURIG D, SMITH D R. Controlling electromagnetic fields [J]. Science, 2006, 312(23):1780-1782.

[2]MARTIN F, FALCONE F, BONACHE J, et al.Miniaturized coplanar waveguide stop band filters based on multiple tuned split ring resonators [J]. IEEE Microwave Wireless Compon Lett, 2003, 13(12): 511-513.

[3]周霞, 汪会波, 董建峰. 超表面的电磁特性研究进展 [J].材料导报, 2016, 30(13): 49-54.

[4]SMITH D R, PENDRY J B, WILTSHIRE M C K.Metamaterials and negative refractive index [J]. Science,2004, 305(5685): 788-792.

[5]SU P, ZHAO Y J, JIA S L, et al. An ultra-wideband and polarization-independent metasurface for RCS reduction [J].Sci Rep, 2016, 6: 20387.

[6]SUN H Y, GU C Q, CHEN X L, et al. Broadband and broad-angle polarization-independent metasurface for radar cross section reduction [J]. Sci Rep, 2017, 7: 40782.

[7]CHEN K, CUI L, FENG Y J, et al. Coding metasurface for broadband microwave scattering reduction with optical transparency [J]. Opt Express, 2017, 25(5): 5571-5579.

[8]吴晨骏, 程用志, 王文颖, 等. 基于十字形结构的相位梯度超表面设计与雷达散射截面缩减验证 [J]. 物理学报,2015, 64(16): 164102.

[9]SHELBY R A, SMITH D R, SCHULTZ S. Experimental verification of a negative index of refraction [J]. Science,2001, 292(5514): 77-79.

[10]韩璐, 王兆娜. 推导广义的反射定律和折射定律的两种方法 [J]. 大学物理, 2013, 32(3): 49-52.

[11]XU H X, TANG S W, LING X H, et al. Flexible control of highly-directive emissions based on bifunctional metasurfaces with low polarization cross-talking [J]. Ann Phys, 2017, 529(5).

[12]ALRASHEED S, FABRIZIO E D. Design and simulation of reflect-array metasurfaces in the visible regime [J]. Appl Opt, 2017, 56(11): 3213-3218.

[13]POLITANO A, CHIARELLO G. Plasmon modes in graphene: status and prospect [J]. Nanoscale, 2014, 6(19):10927-10940.

[14]MITROFANOV O, VITI L, DARDANIS E, et al.Near-field terahertz probes with room-temperature nanodetectors for subwavelength resolution imaging [J].Sci Rep, 2017, 7: 44240.

[15]POLITANO A, VITI L, VITIELLO M S. Optoelectronic devices, plasmonics, and photonics with topological insulators [J]. APL Mater, 2017, 5(3): 035504.

[16]YANG Q, GU J, WANG D, et al. Efficient flat metasurface lens for terahertz imaging [J]. Opt Express, 2014, 22(21):25931-25939.

[17]李勇峰, 张介秋, 屈绍波. 宽频带雷达散射截面缩减相位梯度超表面的设计及实验验证 [J]. 物理学报, 2014,63(8): 084103.

[18]CHENG Y Z, WU C J, GE C C, et al. An ultra-thin dual-band phase-gradient metasurface using hybrid resonant structures for backward RCS reduction [J]. Appl Phys B, 2017, 123(5): 143.

[19]LI Y F, WANG J, ZHANG J, et al. Ultra-wide-band microwave composite absorbers based on phase gradient metasurfaces [J]. Prog Electromagn Res M, 2014, 40: 9-18.

[20]WU C J, CHENG Y Z, WANG W Y, et al. Design and radar cross section reduction experimental verification of phase gradient meta-surface based on cruciform structure [J].Acta Phys Sin, 2015, 64(16): 164102.

[21]YU N F, GENEVET P, KATS M A, et al. Light propagation with phase discontinuities: generalized laws of reflection and refraction [J]. Science, 2011, 334(6054): 333-337.

[22]AIETA F, GENEVET P, YU N F, et al. Out-of-plane reflection and refraction of light by anisotropic optical antenna metasurfaces with phase discontinuities [J]. Nano Lett, 2012, 12(3): 1702-1706.

[23]YU N F, GENEVET P, AIETA F, et al. Flat optics:controlling wavefronts with optical antenna metasurfaces[J]. IEEE J Sel Top Quantum Electron, 2013, 19(3):4700423.

[24]SUN S L, HE Q, XIAO S Y, et al. Gradient-index meta-surfaces as a bridge linking propagating waves and surface waves [J]. Nat Mater, 2012, 11(5): 426-431.

[25]SUN S L, YANG K Y, WANG C M, et al. High-efficiency broadband anomalous reflection by gradient meta-surfaces[J]. Nano Lett, 2012, 12(12): 6223-6229.

[26]CUI T J, QI M Q, WAN X, et al. Coding metamaterials,digital metamaterials and programmable metamaterials [J].Light: Sci Appl, 2014, 3(10): e218.

[27]HUANG C, PAN W B, MA X L, et al. Wideband radar cross-section reduction of a stacked patch array antenna using metasurface [J]. IEEE Antennas Wireless Propag Lett,2015, 14: 1369-1372.

[28]LIU Y, HAO Y W, LI K, et al. Wideband and polarization independent radar cross section reduction using holographic metasurface [J]. IEEE Antennas Wireless Propag Lett, 2016, 15: 1028-1031.

[29]XU H X, TANG S W, MA S J, et al. Tunable microwave metasurfaces for high-performance operations: dispersion compensation and dynamical switch [J]. Sci Rep, 2016, 6:38255.

[30]PAN W B, HUANG C, PU M B, et al. Combining the absorptive and radiative loss in metasurfaces for multi-spectral shaping of the electromagnetic scattering [J].Sci Rep, 2016, 6: 21462.

[31]MA H F, LIU Y Q, LUAN K, et al. Multi-beam reflections with flexible control of polarizations by using anisotropic metasurfaces [J]. Sci Rep, 2016, 6: 39390.

[32]YUAN F, WANG G M, XU H X, et al. Broadband RCS reduction based on spiral-coded metasurface[J]. IEEE Antennas Wireless Propag Lett, 2017, 16: 3188-3191.

[33]范亚, 屈绍波, 王甲富, 等. 基于交叉极化旋转相位梯度超表面的宽带异常反射 [J]. 物理学报, 2015, 64(18):184101.

[34]ZHAO Y, CAO X Y, GAO J, et al. Broadband diffusion metasurface based on a single anisotropic element and optimized by the simulated annealing algorithm [J]. Sci Rep, 2016, 6: 23896.