蝙蝠算法在无线传感器网络节点递增式定位中的应用

束仁义，沈晓波，葛先雷，蔡 俊

(淮南师范学院电子工程学院，安徽淮南，232038)

定位技术是无线传感器网络重要的支撑技术［1］。所谓定位就是确定节点的具体位置，而在无线传感器网络定位技术中，每个节点都有预先确定的位置是不可取的，同时为每个节点配置GPS设备也是不现实的，因为考虑到成本和具体的环境问题。因此，无线传感器网络节点的定位研究在实际应用中具有重要的意义。

定位方法的探索与应用一直以来都备受国内外专家和学者的重视，近年来在定位算法的研究上已取得了一些成绩和进步。例如，江南大学的熊伟丽、唐蒙娜、徐保国提出了一种基于最优加权最小二乘估计的节点定位改进方法，此方法能有效抑制累积误差中测距误差与定位误差带来的影响，提高了节点定位精度［2］;重庆大学的何小敏、熊庆宇、石为人等提出一种基于网格划分的递增式定位算法，该算法能够有效地解决累计误差和能耗问题，提高全网定位的效率［3］;越南海防私立大学的Trong－The Nguyen，Thi－Kien Dao和澳大利亚佛林德斯大学的John F.Roddick等人提出一种基于多目标萤火虫算法的智能定位算法，它能够提高定位精度［4］。总之，无线传感器网络定位算法的研究一直在进行中，尤其在改善定位精度方面将持续跟进，不断更新算法或改进成熟的定位技术。

近年来，业界提出了一种新型的智能算法——蝙蝠算法。蝙蝠算法的基础近似使用以下基本规则［5］:

(1)所有蝙蝠使用回声来感知距离，它们能够以一种不可思议的方式来辨别食物和障碍物;

(2)蝙蝠在某个位置xi，具有最小频率fmin，以速度vi随机飞行，通过变化的波长λ和脉冲响度A0来搜索食物。它们能够自动地调节发射脉冲的波长，其中调节脉冲发射率γ∈［0，1］，它取决于蝙蝠对目标的接近程度;

(3)尽管脉冲响度能够以不同方式来变化，我们均假设脉冲响度变化从一个大的(正的)值A0连续变化到一个最小值Amin。

蝙蝠算法比常见的粒子群算法具有更好的性能［6］，因此文中将蝙蝠算法应用到无线传感器网络节点递增定位方法中，并和常见的三边定位算法进行比较，通过Matlab软件仿真，在三维空间(3D)区域进行定位精度的对比。仿真实验表明基于蝙蝠算法的递增定位较成熟的三边定位算法在定位精度上有所提高。

1 定位技术

1.1 三边测量方法

无线传感器网络节点定位方法可以分为基于距离测量和距离无关两类［7］。最常见的定位方法是基于距离测量的定位方法，距离测量常用RSSI算法，而节点的具体位置坐标通常用三边测量方法获得。

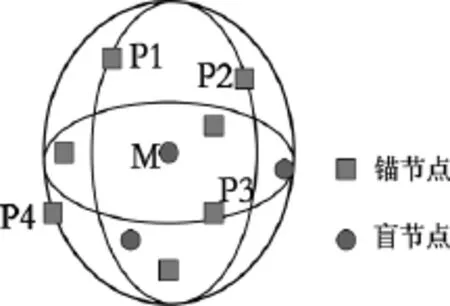
图1 节点定位图示Fig.1 Diagram of node location

节点一般分为锚节点(或称已知节点)和盲节点(或称未知节点)两种。设在一个3D区域内有若干个节点，设某个盲节点M坐标为(x，y，z)，在有效通信半径范围内取四个锚节点 P1、P2、P3 和 P4，对应的坐标分别为 (x1，y1，z1)、

(x2，y2，z2)、(x3，y3，z3) 和(x4，y4，z4) ，四个锚节点刚好位于同一个球面上，而盲节点则是球心，如图1所示。

假设测得M到P1、P2、P3和P4的距离分别为d1、d2、d3和d4，根据距离公式可得:

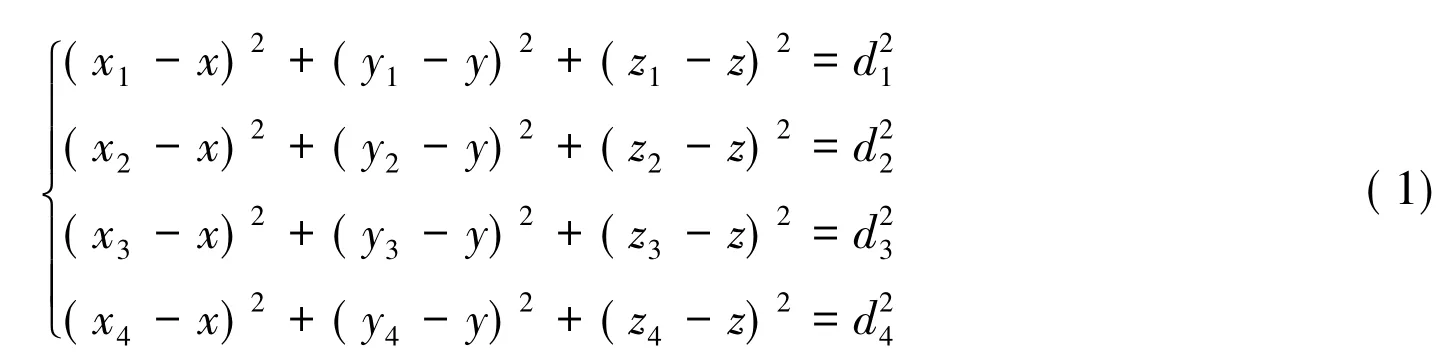
求得盲节点M的坐标为:

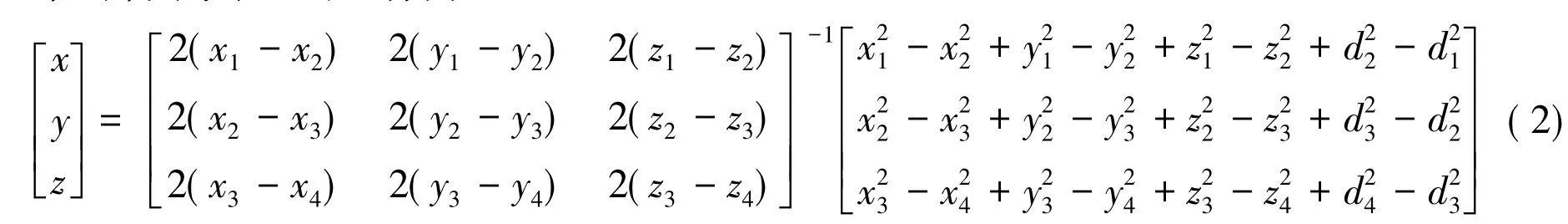
1.2 逐步递增式定位

无线传感器网络节点定位方法也可以分为并发式和递增式。如果节点数目多，覆盖范围广，通过人工测量手段获取大量节点的位置信息是不可取的，这时往往采用递增式定位方法［8］。逐步递增式定位的基本思想是:初始少量节点作为参考节点，其余节点均为未知节点，在通信范围内，通过参考节点来求未知节点的坐标，再将已定位的未知节点作为参考节点并进行下一级的定位，逐级定位直至所有的盲节点都已成为已知节点。

假设3D区域内有L个节点，初始参考节点数为L0(4≤L0≤L)，L和L0均为正整数，则盲节点数目为L－L0。设初始参考节点集合为:

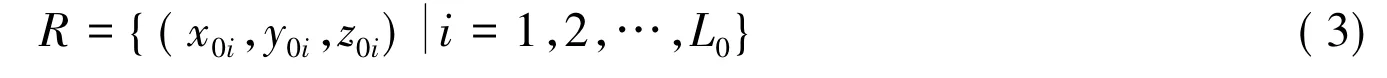
设逐步递增定位中第j(j=0，1，2，…，k)次参考节点的集合为:

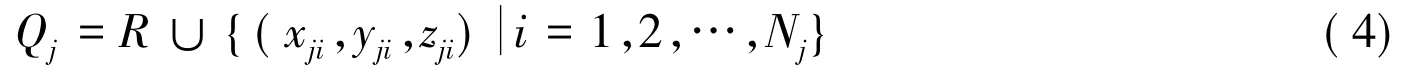
其中N1，N2，…，Nj分别表示每一步递增定位的节点。用T(.)表示递增式定位算法，则有:

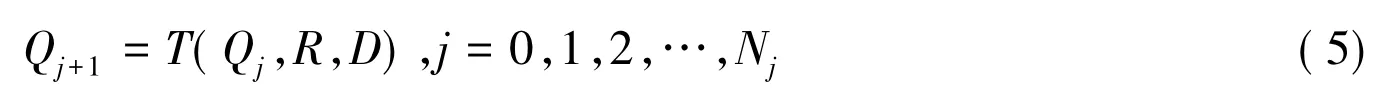
其中D表示测距集合，以矩阵形式存储任意两个节点的距离值，因此D是一个方阵。由于每个节点都有唯一的标识号，故D可写成:

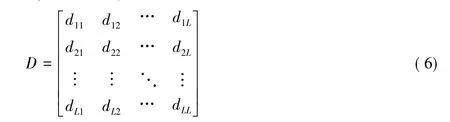
其中dmn(1≤m≤L，1≤n≤L)表示标识号第m个节点到第n个j节点的距离，则有关系式:D=DT;dmn=0(m=n)。

2 蝙蝠算法

根据蝙蝠算法遵循的基本规则，我们模拟蝙蝠的虚拟运动。首先我们在3D中对蝙蝠的位置和飞行速度进行实时控制并更新，假设在t时刻的位置和速度分别记为和，则有:

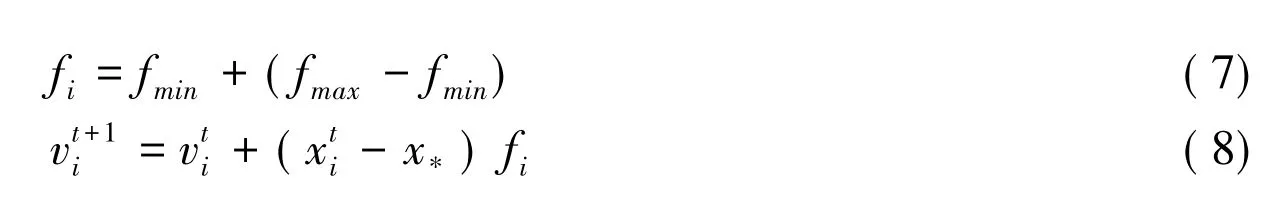
其中 β∈［0，1］，和分别表示t+1时刻的速率与位置，x*是当前全局的最优解。

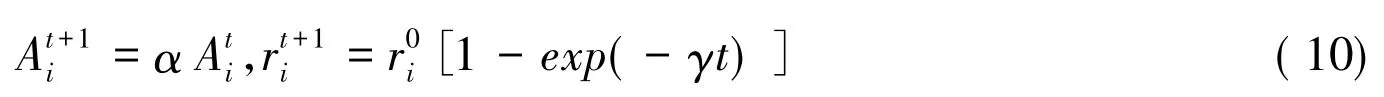
其中α和γ是常数。对于任意0＜α＜1以及γ＞0，当t→!时有:

因此，蝙蝠算法的伪代码［9］描述如下:初始化蝙蝠种群数xi和vi(i=1，2，…，n);初始化频率fi，脉冲发射率ri和声音响度Ai;while(小于最大迭代次数)

通过调节频率来产生新的解;

根据式(7)、(8)、(9)更新速率和位置;

if(rand＞ri)

在最优解中选择一个解;

从选择的最优解中产生一个局部解;

end if

通过随机飞动产生一个新解;

if(rand＜Ai＆f(xi)＜f(x*))

接受这个新解;

增加ri并减少Ai;

end if

对所有蝙蝠进行排列并找到

当前最好的解x*;

end while

3 算法仿真

3.1 基于蝙蝠算法的递增式定位流程

由于实际测距可能存在误差，式(1)中的距离值就不是真实值，求出的位置点的坐标也就有偏差，因此3D定位问题可以转化为求目标函数

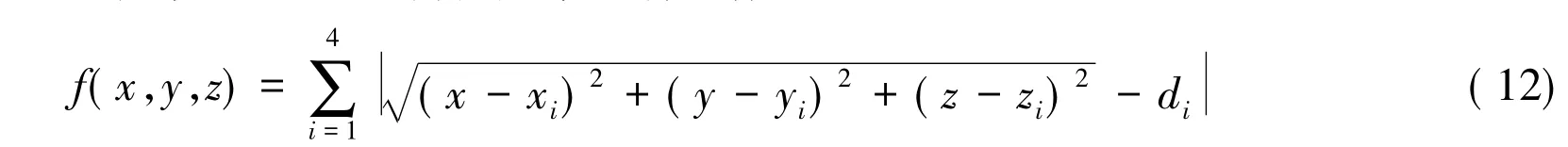
最小值的优化问题，我们可以利用蝙蝠算法去求解。

假设盲节点的真实位置为(x，y，z)，根据定位算法求得的解为(x'，y'，z')，则定位误差ε定义为:

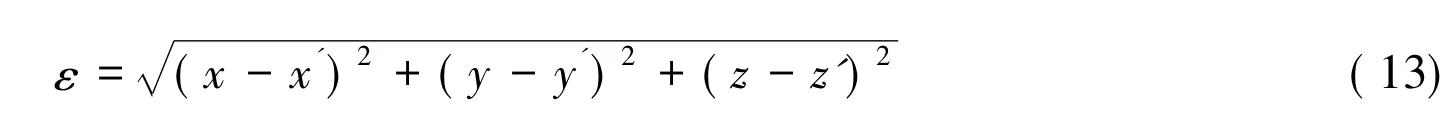
算法流程如下图2所示:

3.2 仿真实验

在Matlab 2010b中进行仿真实验，3D仿真区域为50m×50m×50m，随机分布200个节点，初始参考节点数为4，其余均为盲节点数。蝙蝠算法的参数及对应的初始值如下表1所示。

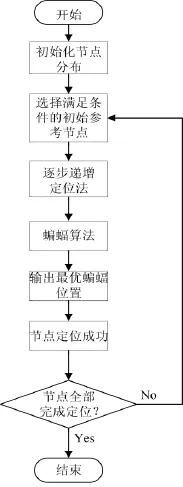
图2 基于蝙蝠算法递增定位流程图Fig.2 Flowchart of increasing localization based on bat algorithm

表1 蝙蝠算法参数Table 1 Parameters of bat algorithm

假设节点在无测距误差且通信距离不限(即递增定位级数为1)环境下利用蝙蝠算法进行定位，得到如下图3所示的仿真结果。

图3仿真结果表明基于蝙蝠算法的无线传感器网络节点定位可以取得很好的定位效果，因此，可以将蝙蝠算法应用到递增式定位算法中。假设节点在有测距误差且通信距离不限环境下，再利用蝙蝠算法定位并和三边定位法进行比较，得到如图4所示的定位节点误差对比图。

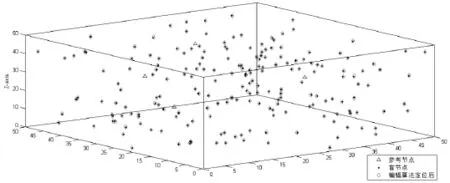
图3 基于蝙蝠算法3D定位仿真Fig.3 Simulation of positioning based on bat algorithm in 3D

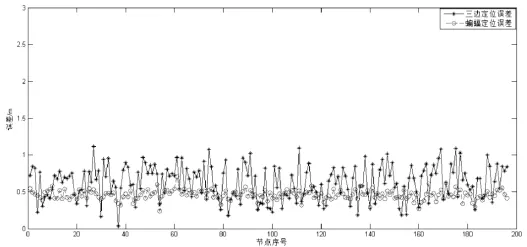
图4 基于三边测量法与蝙蝠算法初步定位误差对比Fig.4 Comparison of positioning error in the first step based ontrilateration and bat algorithm

图4表明在有测距误差的环境下，基于蝙蝠算法的定位要比三边测量法的定位在总体定位精度上要高。假设节点通信距离为30m，则在测距误差环境下，由于递增式定位随着级数的增加，定位误差也累积增大，将三边测量法与蝙蝠算法各级节点比较，得到如图5所示的节点误差对比图。图5表明在级数开始的时候，基于蝙蝠算法的定位要比三边测量法的定位在定位精度上要稍好些，但是随着累计误差增加，定位精度也逐渐降低，甚至某些点的定位效果已经不理想。

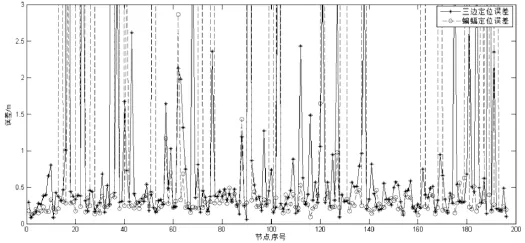
图5 基于三边测量法与蝙蝠算法多级递增定位误差对比Fig.5 Comparison of positioning error step by step based on trilateration and bat algorithm

综上实验结果可知:基于蝙蝠算法和测距原理的逐步递增定位在4个参考节点的初始条件下能够定位出所有的盲节点。因此，通过和其它文献提出的定位算法比较，文中应用的定位算法比文献［2］的递增定位需要更少的初始参考节点，相对文献［3］的算法产生更少的累积误差且搜索速率更快，定位耗时短。

4 结束语

针对传统的三边测量法在定位精度上的不足，提出将基于全局优化的蝙蝠算法应用到无线传感器网络节点递增式定位中。通过实验仿真，蝙蝠算法可以很好地应用在3D定位中，相比于三边测量法，定位精度有较明显地改善，特别在递增定位的前几级，累积误差也相对较小。因此，蝙蝠算法为无线传感器网络节点递增式定位提供了一种较好的技术方案。

参考文献:

［1］孙利民.无线传感器网络［M］.北京:清华大学出版社，2005.

［2］熊伟丽，唐蒙娜，徐保国.一种用于无线传感器网络节点递增式定位的新方法［J］.传感技术学报，2011，24(04):576－580.

［3］何小敏，熊庆宇，石为人，等.基于网格划分的递增式定位算法［J］.计算机应用研究，2012，29(02):687－689.

［4］NGUYEN TT，PAN JS，CHU SC，et al.Optimization Localization in Wireless Network Based on Multi－Objective Firefly Algorithm［J］.Journal of Network Intelligence，2016，1(04):130－138.

［5］YANG X.Bat Algorithm for Multi－objective Optimization［J］.International Journal of Bio－Inspired and Computation，2011，3(05):267－274(8).

［6］李煜，马良.新型全局优化蝙蝠算法［J］.计算机科学，2013，40(09):225－229.

［7］王行甫，刘志强，黄秋原，等.WSN中一种改进的边界盒定位算法［J］.计算机工程，2011，37(20):57－59.

［8］CHEN S，YU Y.Incremental localization algorithm based on distance matrix in wireless sensor networks［J］.International Journal of Information and Communication Technology，2017，11(01):38－47.

［9］YANG X S.Nature－Inspired Metaheuristic Algorithms:Second Edition［M］.Beckington:Luniver Press，2010.